单兵野营装备物资携行问题研究

文/史磊　梁伟祥　李鹏飞　谢友政



单兵野营装备物资携行问题研究

文/史磊梁伟祥李鹏飞谢友政

摘 要：本文针对单兵野外宿营需要携带装备物资的实况，首先提出野营装备物资携行筛选的基本原则。然后在问题描述的基础上，构建出问题模型并给出求解算法，通过实际算例验证了模型的有效性，研究成果可为提升单兵野外宿营水平提供科学支撑。

关键词：野营装备；单兵；携行；动态规划

引言

随着武警部队职责使命的不断拓展，多样化任务对包括营房保障在内的后勤保障的要求越来越高。鉴于武警部队担负任务的特殊性，致使任务官兵宿营的客观环境和现实条件尚不太乐观，特别是实施整编宿营保障的要求越来越高，保障的难度也越来越大。因此，单兵携行宿营装备物资进行自我保障宿营的模式逐渐受到部队和官兵个人的青睐。但是，任务官兵如何携行宿营装备物资的数质量问题业已开始引起有关首长和相关部门的关注。本文即是在考虑任务官兵个体除携行必要处置任务的装备外，如何在身体允许的条件，携行合理的宿营装备物资，较为有效地保障宿营进行有益探讨，以为武警部队遂行多样化任务宿营保障提供物资基础和可供养精蓄锐、恢复战斗力的平台。

1.单兵携行野营装备的筛选原则

当前能够满足遂行任务官兵宿营需要的装备物资种类很多，但是鉴于单兵个体携行能力有限的客观实况，能够科学地在琳琅满目、种类繁多、数量巨大的宿营装备物资中确定必要的携行装备物资，成为制约拟订最优携行方案的最大障碍。应该如何筛选既能携带，又在野外宿营时有时使用的装备物资呢？

1.1效用性原则

任务官兵携带的装备物资对于野外宿营必须是具有效用的。而且在其它方面，如重量、操作难易等方面相同时，应该优先携带对于宿营来说效用相对较大的那类装备物资。至于最终携带几件，是否携带等尚需考虑其它因素，如任务官兵的携行能力是否允许，是否已确定携行具有替代功能的装备物资等。

1.2替代性原则

替代性即两类或多类装备物资，对于同意需求具有完全相同的功能，只要选取其一即可满足需要。在野外宿营装备物资中，如充气垫与防潮布，应急灯与手电筒、蜡烛等之间均存在所谓的替代性关系。对于具有替代功能的装备物资应结合宿营，可能面临的环境条件、任务需求、野营持续时间等情况有针对性的确定，如风多地域，则最好不要携带蜡烛作为照明物资。

1.3互补性原则

互补性原则是指不同类装备物资必须同时具备时，才能有效地发挥出其所具有的功能。如照明用的手电筒、电池、灯泡与手电筒即具有互补关系。如果野外宿营中确定携带手电筒，则必须考虑必要的备用电池和灯泡等，以防止由于其中某一物资出现问题而导致整个功能的丧失。

2.问题描述及建摸

一单兵外出执行任务需要野外宿营时，需要携行必要的宿营装备物资。已知所能随身携行的背囊重量限度为Q，现有n种宿营装备物资可供选择装入背囊。第i种宿营装备物资件数为xi，其单件重量为ui，宿营效用指标为ci，则该单兵应如何选择携行各种宿营装备物资，才能使其总宿营效用最大［1］？

在构建模型前，首先给出以下假设：

假设一：每件宿营装备物资对官兵个人的宿营效用可以排出高低次序。

假设二：官兵个人携行的宿营装备物资的每个组合均可满足单兵的宿营需求。

假设三：单兵携行的宿营装备物资的体积均在允许的范围内，问题考虑的主要因素主要是装备物资的宿营效用和重量，其它方面可以忽略不计。

单兵携行野营装备物资的数学模型为［2］：

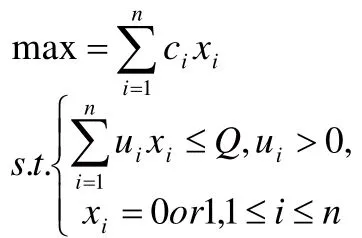
3.算法设计

根据动态规划的条件描述，单兵携带宿营装备物资的情况是一种典型的0～1一维背包问题，约束条件宿营装备物资器材的承重，因此，可用动态规划方法讨论其求解过程及算法设计。本模型求解的基本思想，是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解，用一个表来保存记录所有已解决的子问题的答案，在需要的时候再找出已求得的答案，避免重复的计算，其理论基础上最优化原理［3］。主要步骤是：划分阶段，确定阶段的状态；确定决策变量、权函数及指标函数；建立状态转移方程；根据最优化原理建立递归方程；自底向上递推逐步求解［4］。

3.1确定阶段数：阶段可以按照物资器材的选择过程来划分，可将选择物资器材A、B、C、D、E……的过程分别作为第1、2、3、4、5……、n阶段，则阶段变量K=1、2、3、4、5……、n；

3.2确定状态变量：sk为第K阶段开始时第K种物资器材的可选重量，于是，0≤sk≤Q，s1=Q；

3.3确定决策变量：xk为第K阶段第K种物资器材的选择件数，由于本类问题中，每件物资器材只有一件，于是xk=0或1，也可以写作0≤xk≤1，取整；

3.4阶段效应为第k阶段所选物资器材的宿营效用，不妨记作gk（xk）；

3.5状态转移方程xk+1=xk-ukhk，k=1，2，3，4，5；其中uk第k种物资器材的单位重量；

4.实例应用

某侦察兵准备外出执行任务，背囊中有A、B、C、D、E五件备选宿营装备物资，其重量和宿营效用如表一所示，为了便于行动，假定侦察兵个人负载宿营装备物资总重不得超过13公斤，求该侦察兵在确保完成任务的前提下，能使宿营效用最大的宿营装备物资构成方案。

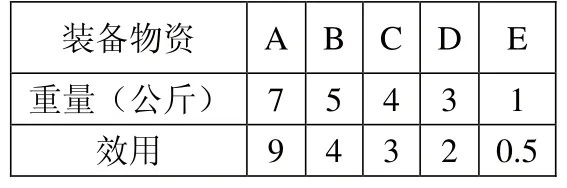
表一　已知数据信息

可选宿营装备物资的重量按1公斤为间隔离散化，则状态可能集为0，1，2，…，12，13；

按照3所设计的算法，采用表格形式进行逆序求解，见表二：

x K g ( x ) + f k k k 1 　 + + ( s k 1 ) 0 1 　( ) f5s 　 x*55 s k 5 0 1 2 3 4 5 6 7 8 9 1 0 1 1 1 2 1 3 0 -0 0 . 5 0 0 . 5 0 0 . 5 0 0 . 5 0 0 . 5 0 0 . 5 0 0 . 5 0 0 . 5 0 0 . 5 0 0 . 5 0 0 . 5 0 0 . 5 0 0 . 5 0 0 . 5 0 . 5 0 . 5 0 . 5 0 . 5 0 . 5 0 . 5 0 . 5 0 . 5 0 . 5 0 . 5 0 . 5 0 . 5 0 1 1 1 1 1 1 1 1 1 1 1 1 1

表二　单兵野营装备物资携行问题求解表

最优状态序列，求解的反向追踪过程如下：

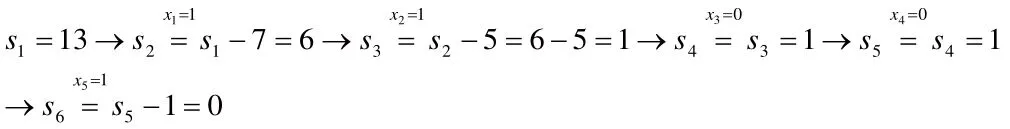
计算结果表明，最好的选择方案是：选A装备物资1件，B装备物资1件，E装备物资1件，而不选C、D两种装备物资，此时携带的装备总重量恰为13公斤，总效用达到最大为13.5。

5.结论

通过分析影响单兵筛选野外宿营所需携带装备物资种类原则的基础，借助动态规划方法，构建出针对单兵野外宿营需要携行装备物资的模型，并通过具体实例进行应用，得知采用此方法可以科学、高效地帮助单兵个体对于其野外宿营需要携行的装备物资进行科学决策。既能防止单兵个体过度的携带物资，又可较为满意地为单兵个体提供优越、舒适的宿营平台，以减少单兵个体战斗力的非战斗损失，直至促进其战斗力的有效生成。

武警后勤学院后勤装备技术项目（编号：WJZ201402）

武警后勤学院教学改革重点项目（编号：WHJZ201505）

（作者单位：武警后勤学院）

参考文献

［1］于淼.“背包问题”算法设计及分析［J］.科学计算与信息处理，2010，313（2）：128～130.

［2］周本达，陈明华，任哲.一种求解0～1背包问题的新遗传算法［J］.计算机工程及应用，2009，45（30）：45～48.

［3］应莉.0～1背包问题及其算法分析［J］.计算机与现代化，2009，166（6）：24～26.

［4］刘继，夏定纯.用动态规划法与回溯法实现0～1背包问题的比较［J］.科技信息，2010（19）：458

［5］徐渝，贾涛.运筹学（上）［M］，清华大学出版社2005.