基于CSS的室内测距优化技术*

王佳伟,王敬东,赵　强,魏雪迎

(南京航空航天大学自动化学院,江苏南京　211106)

基于CSS的室内测距优化技术*

王佳伟,王敬东,赵强,魏雪迎

(南京航空航天大学自动化学院,江苏南京211106)

摘要:基于CSS(Chirp Spread Spectrum,线性调频扩频)技术的无线测距是基于TOA(time of arrival,到达时间)的测距方法,在室内应用中,存在较多的NLOS(Non-Line of Sight,非视距)干扰,因此测距精度低。针对这个问题,对传统卡尔曼滤波进行改进,将NLOS误差加入状态向量进行估计,进行两步卡尔曼滤波,从而抑制NLOS误差对测距的影响。考虑到LOS(Line of Sight,视距)和NLOS并存的情况,对两步卡尔曼滤波算法进行改进,在第二步滤波中对NLOS误差鉴别和滤波处理部分做出改进,并应用到测距系统中。实验表明,利用该测距优化方法,TOA测距的精度和抗干扰能力得到了明显的提高。

关键词:线性调频扩频;到达时间;非视距误差;卡尔曼滤波

基于CSS(Chirp Spread Spectrum,线性调频扩频)的节点定位技术是一种基于TOA(time of arrival,到达时间)测距[1]的定位技术,被广泛应用于人员的实时监控、室内人员的移动监测、监狱人员定位管理、矿井下人员和设备的定位等方面。

在室内定位应用中,TOA测距的精度直接影响到定位结果,而测距精度受多种误差的影响,包括测距双方的时间同步误差、量测噪声误差和非视距(NLOS,Non-Line of Sight)传播误差,其中影响最大的是NLOS传播误差。而NLOS误差将对测距值产生较大的影响,严重降低了室内测距的精度,因此需要采取措施抑制NLOS误差对测距的影响。

目前,抑制NLOS误差的常用方法可以分为两类：第一类方法就是采用TOA与其他信号参量(如波达方向,信号强度)进行数据融合的方法[2-4],因为采用了另一个维度的信息,有可能得到较好的结果。但这类方法需要增加另一维度的测量硬件,增加了成本和系统的复杂度,不利于应用；另一类方法是直接分析TOA测距值的方法。文献[5]提出了一种基于TOA测量值概率分布的NLOS误差鉴别方法,通过检验测量距离的分布来鉴别接收信号中是否存在NLOS误差,但由于室内环境的复杂性,测量值的概率分布函数估计难度大,因此该方法在实际应用中并不实用。文献[6]采用多参数的机器学习方法对超宽带信号进行NLOS鉴别和测距误差消除,具有较好的适应性和鲁棒性,但算法复杂度增大实时性不强。文献[7-8]利用改进的卡尔曼滤波抑制NLOS误差,然而由于NLOS误差的随机性,在视距(LOS,Line of Sight)与非视距传播同时存在的环境中,对误差的抑制效果不佳。

针对两种方法的优缺点,本文采用直接分析测距值的方法抑制NLOS误差。文章首先对NLOS误差进行分析,针对NLOS误差特性,对卡尔曼滤波器进行改进,以抑制NLOS误差,并对NLOS误差的鉴别和卡尔曼滤波处理模块做出改进,使得系统在LOS与NLOS混合环境下都具有较高的测距精度。

1室内测距误差模型及统计分析

影响TOA测量值的误差中，时间同步误差属于系统误差,文献[9]介绍的双边两路测距算法可以很好地抑制时间同步产生的误差。量测噪声误差是测量过程中的随机误差,属于零均值的高斯白噪声,可以通过一定的滤波平滑技术进行抑制。

当信号的直接传播路径被遮挡时,无线信号的传播路径就会变成信号经过反射和折射等方式传播的路径,由此而产生的正向的非高斯白噪声的误差就是NLOS误差。若将包含这样的正值的测距误差分量的TOA测距结果代入室内定位系统中,必然会产生较大的定位误差。

通过对室内环境误差的分析可以建立室内测距模型,若r(t)表示在t时刻从移动节点到锚节点的距离测量值,则r(t)等于真实距离d(t)与量测噪声误差n(t)和NLOS误差NLOS(t)之和,如式(1)所示。

r(t)=d(t)+n(t)+NLOS(t)

(1)

其中，n(t)为零均值高斯变量,NLOS(t)为正随机变量。为了研究室内环境下各类误差对测距精度的影响,本文在室内环境下进行了大量实验,实验中的NLOS误差采用人为遮挡进行模拟,部分实验结果如图1所示。

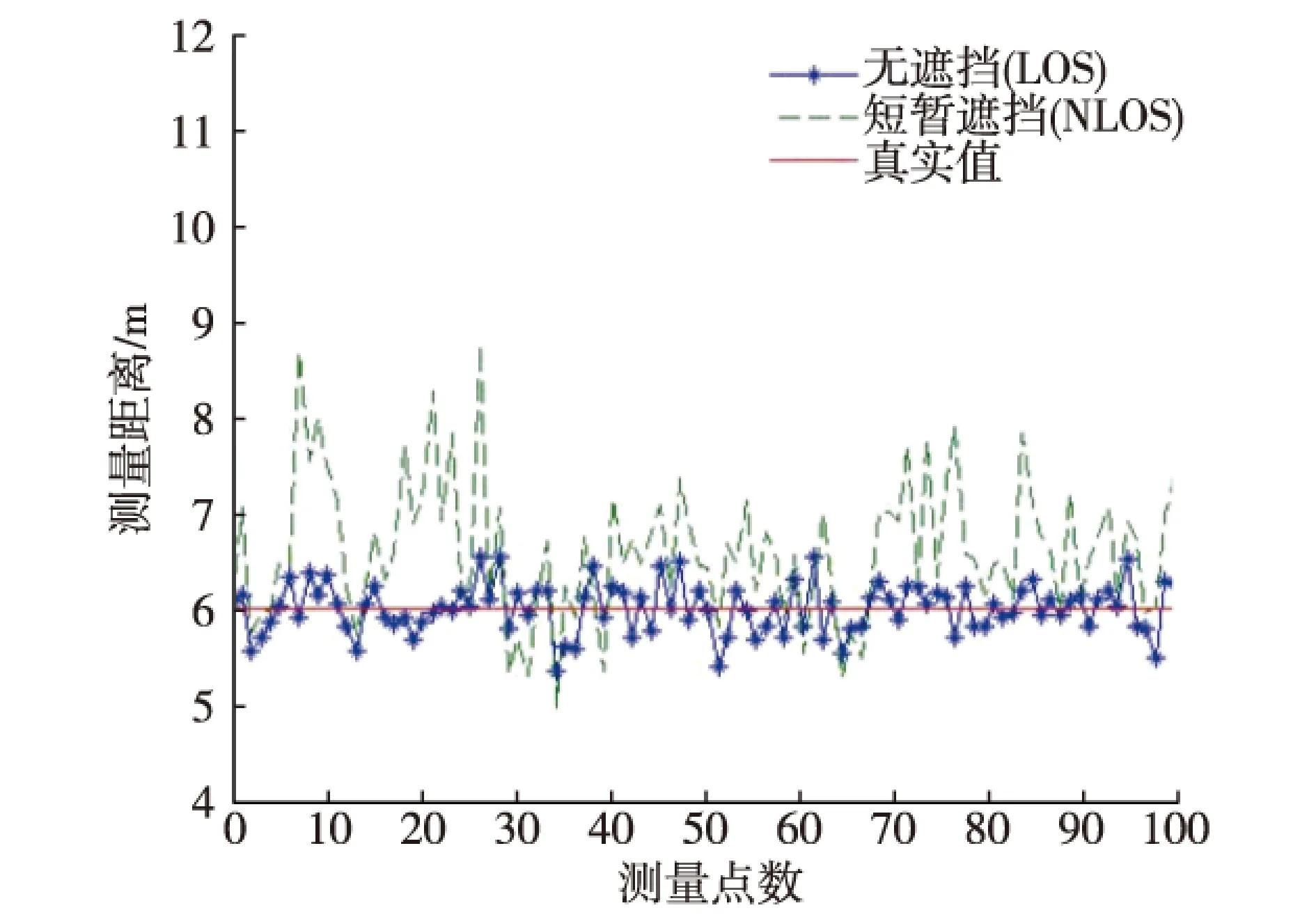
图1　有随机遮挡干扰与无随机遮挡干扰下测距结果

如图1所示,在无随机遮挡情况下,同一位置的TOA测量值围绕某一中心值上下微弱波动且幅度较小,而当环境中存在短暂遮挡干扰时,TOA的测量值波动较大,部分测量值会远远偏离正常值,且总是正向偏离真实值。在无干扰情况下测距误差可以认为是一组白噪声,可以通过平滑滤波方法滤除,存在遮挡干扰时,测距值严重偏离真实值,此时误差即NLOS误差,需要特殊方法鉴别和滤除。

NLOS误差具有随机性、正值性和独立性。首先,由于TOA测量值中NLOS误差的分布与电波传播路径上障碍物的分布有关,所以NLOS误差具有随机性的特点。其次,由于NLOS误差是无线电波在传播途中遇障碍物发生超量延迟所致,所以TOA中的NLOS误差总是正值。最后,由于NLOS误差和量测噪声误差的产生原因不同,因此是相互独立的。

室内环境的复杂性决定了NLOS传播在室内环境不可避免,而NLOS误差是影响室内定位系统性能中最主要的因素,因此要提高室内定位系统的定位精度,就必须研究抑制NLOS误差的方法。

2卡尔曼滤波算法

卡尔曼滤波[10]是最佳线性递推滤波器,广泛应用于机器人导航、控制、传感器数据融合等不同领域[11-12]。卡尔曼滤波器的基本思想就在于状态方程与量测方程分别表示未知状态的转移过程和测量系统输入与输出的关系,从而把某个时刻的状态值与当前以及以前时刻的测量值联系起来。

本文采用卡尔曼滤波对TOA测量值进行滤波处理,假设每个周期T获取一次TOA测量值,卡尔曼滤波的状态方程和量测方程为

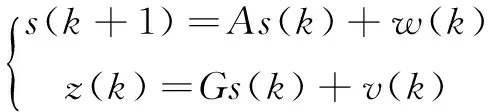
(2)

卡尔曼滤波器的迭代过程如式(3)～(8)所示。

(3)

3基于改进的卡尔曼滤波的NLOS误差抑制

在LOS环境下,卡尔曼滤波器可以在一定程度上消除TOA测量值中的系统量测噪声误差。但是,在 NLOS环境下,偏差较大的测量值不仅使当前时刻的TOA估计发生较大偏差,并且由于卡尔曼滤波器的记忆性,使后续的TOA估计都受到严重影响。因此,需要在传统的卡尔曼滤波基础上做出改进,以抑制NLOS误差。

3.1两步卡尔曼滤波

针对TOA测量值中的NLOS误差,传统的卡尔曼滤波不能很好地抑制NLOS误差,因此本文将NLOS误差加入卡尔曼滤波的状态向量中,采用两步卡尔曼滤波对测距值进行滤波,以抑制NLOS误差。

首先,由于NLOS误差与标准测量误差之间具有相互独立性,因此可以将NLOS误差单独分离出来,加入到待估计的状态变量中,通过卡尔曼滤波递推过程估计出NLOS误差。NLOS误差的系统模型可以建立为

b(k+1)=βb(k)+wb(k)

(4)

其中，b(k)为待估计的NLOS误差,β是NLOS环境变化的常量,由实验测得,wb(k)为NLOS误差估计值的过程噪声向量,因此加入了NLOS误差估计值的卡尔曼滤波算法中各矩阵、向量的设置如下:

(5)

由式(5)可知,通过设置NLOS误差为第三个状态量,经过卡尔曼滤波的迭代过程,可以估计出测量过程的NLOS误差分量,根据b(k)的值判断NLOS误差并修正测量估计值r(k)。由于NLOS误差的非负性，决定了对于计算中b(k)的取值需要重新考虑。若b(k)>0,即可认为在该点上出现了的NLOS误差,此时不改变b(k)的值,并将其应用到测距值修正中。若b(k)≤0,则与NLOS误差非负性相矛盾,此时可以认为NLOS误差为零,即在迭代过程中将小于零的误差估计值强制置零,如式(6)所示:

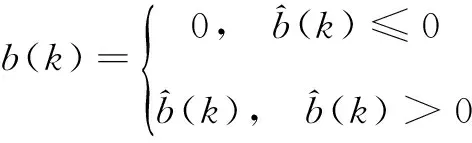
(6)

得到NLOS状态误差的估计值后,将TOA测量值的状态估计值减去估计的NLOS误差值,即可得到第一步滤波结果。经过了第一步的滤波,测量值中的NLOS误差得到了抑制,也就实现了测量值的LOS重构。

经过第一步卡尔曼滤波处理后的TOA测量值初步抑制了NLOS误差,但由于系统中量测噪声、时钟误差等标准测量误差的存在,还需要进行下一步的处理,即第二步的卡尔曼滤波。一般的标准测量误差服从均值为零的正态分布,可以利用标准卡尔曼滤波对测距值进行进一步的平滑处理。第二步卡尔曼滤波器用已经初步消除NLOS误差的TOA测量值作为输入,进一步获得更精确的TOA估计。这一步中各矩阵、向量的设置同传统的卡尔曼滤波方法。

由于该方法利用两步预测的方法对TOA测距值进行滤波处理,首先对NLOS误差进行估计,对于NLOS误差严重的环境中能够获得较好的滤波效果。

在室内进行测距实验,通过人为在两个节点之间走动造成短暂遮挡形成NLOS环境,测距结果利用两种卡尔曼滤波算法对实验数据进行滤波处理,处理结果如图2。

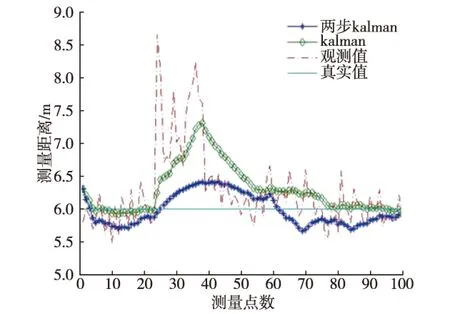
图2　改进的卡尔曼滤波效果图

如图2所示,在测量中存在NLOS干扰时,两步卡尔曼滤波的滤波较经典的卡尔曼滤波效果更好,对于NLOS误差的抑制能够取到一定的效果。但从图中未出现明显大偏差的测距数据的滤波效果看,两步卡尔曼滤波效果逊于经典的卡尔曼滤波的滤波效果,且可能产生一定的过修正。这是因为在LOS环境中不存在NLOS偏置误差,在滤波过程中添加多余的NLOS状态分量将导致状态转移模型和量测方程模型的不匹配,因此在测距中精度有所下降。

3.2改进的两步卡尔曼滤波算法

两步卡尔曼滤波在非视距环境中效果较好,能有效抑制NLOS误差对滤波结果的不利影响。然而,移动节点也会经常遇到在视距环境中工作的情况。在视距环境中,两步卡尔曼滤波相比经典的卡尔曼滤波的效果较差,因此需要对两步卡尔曼滤波过程进行改进,使之适应LOS和NLOS共存的环境。

要使滤波算法适应不同的测距环境,必须对LOS/NLOS环境鉴别部分做出改进。常用的NLOS误差鉴别技术,如Wylie法[13],需要利用TOA的历史测距值,鉴别方法的计算量比较大,不适用于实时的定位系统。本文考虑到卡尔曼滤波的递推性,对两步卡尔曼滤波过程进行改进,利用第一步NLOS误差的估计来鉴别测距环境是否为非视距环境。

原来的两步卡尔曼滤波算法根据误差估计值的正负判断环境中是否存在NLOS误差,本文对此作出改进,设定一个NLOS误差阈值ε,将滤波器估计的NLOS误差状态分量与阈值比较,若大于阈值则判定此刻TOA测量值中含有NLOS误差,若小于阈值则可以判定此时的TOA测量环境为LOS环境。判断结果如式(7)所示:

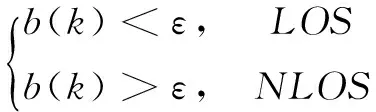
(7)

由于卡尔曼滤波过程中,对于状态向量的估计存在一定的误差干扰,产生正的估计值并不意味着系统的状态属于NLOS环境,因此阈值ε的选取应该考虑具体的实验环境。由于阈值受到估计误差的影响,本文考虑利用LOS环境下测距标准差来确定阈值ε,即通过在LOS环境下进行大量实验,计算测距值的标准差,取平均值σm,令ε=σm。

由于在LOS环境中不存在NLOS偏置误差,在滤波过程中添加多余的NLOS状态分量将导致状态转移模型和量测方程模型的不匹配。鉴于这个原因,本文在两步卡尔曼滤波开始之初保存上一次迭代的估计结果,在第二步卡尔曼滤波开始时,若判定TOA测量环境为LOS环境,则忽略第一步卡尔曼滤波估计结果,利用保存的估计结果对测量值直接进行卡尔曼滤波。通过NLOS环境的鉴定来选择第二步卡尔曼滤波中所使用的方法,从而使该算法适应LOS和NLOS共存的环境。

4实验分析及验证

为了验证本文提出的改进的两步卡尔曼滤波算法的性能,本文进行两组实验,实验环境宽敞节点附近不存在遮挡的干扰,人为地在两个测距节点中间走动形成遮挡来模拟NLOS环境。实验的测距范围为[0，20m],节点间距从 1m处开始测量,每隔1m测量100组数据,每组数据间隔1min进行,并且借助Matlab软件对数据进行处理和分析。

首先进行第一组实验,实验中的环境为模拟的NLOS环境,实验对两步卡尔曼滤波和改进的两步卡尔曼滤波算法估计的NLOS误差进行比较,图3是针对6m测距距离时的实验结果。

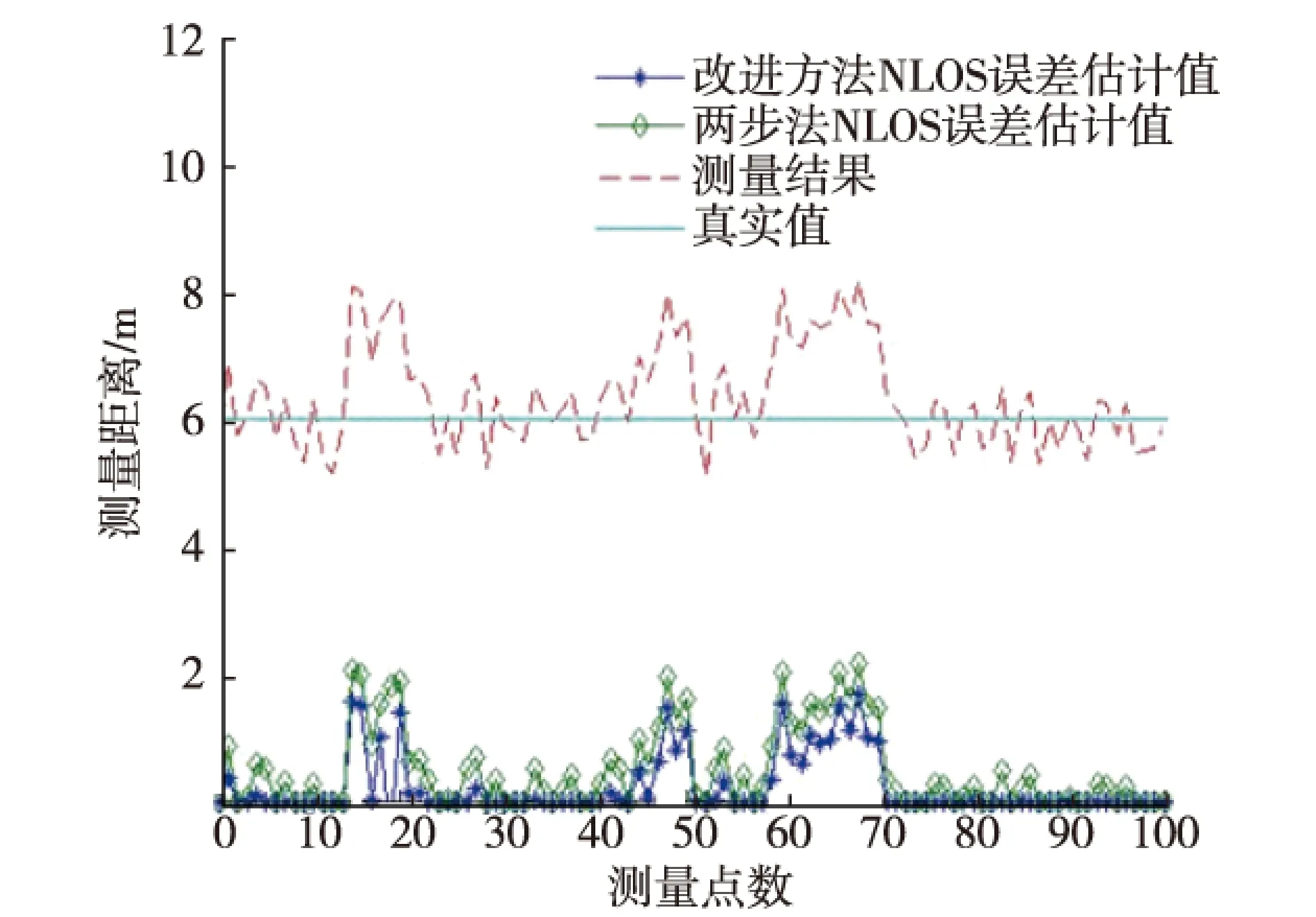
图3　两种卡尔曼滤波算法NLOS估计性能

从图3可以看出,两种算法均能较好地识别NLOS误差,因此在NLOS环境下两种算法均能得到较高的测距精度。但从图中可以看出,两步卡尔曼滤波由于根据估计结果正负来决定NLOS误差,将产生一些误识别,将一些量测噪声识别为NLOS误差。而改进的NLOS误差由于加入了误差评价阈值,一定程度上抑制了过程噪声对NLOS误差估计的影响,因此,在实际LOS/NLOS混合的环境中具有更优的识别性能。

第二组实验分别在LOS和NLOS环境下进行测距实验,分别采用经典卡尔曼滤波、两步卡尔曼滤波和改进的两步卡尔曼滤波方法对测距值进行滤波处理。本文实验结果如图4、5所示。

图4　LOS环境下算法性能比较

图5　NLOS环境下算法性能比较

如图4所示,在LOS环境下,经典的卡尔曼滤波和本文提出的改进的两步卡尔曼滤波算法具有较小的测距误差。在20m的测距范围内,经典的卡尔曼滤波算法的最大测距误差为1.17m,改进的两步卡尔曼滤波算法的最大测距误差为0.95m,而基于两步卡尔曼滤波算法的最大测距误差则达到1.65m。这是因为,LOS环境中,经典的卡尔曼滤波具有较好的平滑效果,而两步卡尔曼滤波由于增加的NLOS状态分量使得测距模型改变。而NLOS环境下的实验结果如图5所示,其中两步卡尔曼滤波和本文改进算法的测距误差较小。在20m的测距范围内,两步卡尔曼滤波的最大测距误差为0.98m,本文改进算法的最大测距误差为0.93m,而基于经典卡尔曼滤波算法的最大测距误差则达到2.25m。

实验结果表明,本文提出的改进的两步卡尔曼滤波算法具有较好地测距误差抑制效果,由于加入了NLOS鉴别,在LOS和NLOS环境下都具有较高的定位精度。

5结束语

本文以CSS测距优化思想为指导,在不增加定位硬件成本的基础上以提高测距精度和测距稳定性为主要目标。实验表明,本文改进的卡尔曼滤波算法能够较好地实现LOS/NLOS环境的鉴别,在LOS与NLOS环境下都具有较高的测距精度。因此,本文的算法在室内实时定位系统中能够较好的提高定位精度,且算法复杂度不高具有较好的实时性,能够很好地应用在未来的室内无线定位技术中。

参考文献:

[1]徐彤阳. NLOS环境下无线传感器网络TOA定位算法[J]. 计算机工程, 2013(12):93-96.

[2]Wang Z, Zekavat S/. Omnidirectional Mobile NLOS Identification and Localization via Multiple Cooperative Nodes[J]. IEEE Transactions on Mobile Computing, 2012, 11(12):2047-2059.

[3]徐彤阳. 基于减法聚类的TOA/AOA定位方法研究[J]. 电子测量技术, 2013, 36(10):91-93.

[4]Wann C D, Chin H C. Hybrid TOA/RSSI Wireless Location with Unconstrained Nonlinear Optimization for Indoor UWB Channels[C]∥2007 IEEE Wireless Communications and Networking Conference， 2007:3940-3945.

[5]王琦琦, 吴虹, 周微,等. 一种基于测量距离分布的NLOS鉴别方法[C]∥第四届中国卫星导航学术年会论文集-S3精密定轨与精密定位， 2013.

[6]李伟杰, 张霆廷, 张钦宇. 基于机器学习的超宽带NLOS鉴别方法[J]. 计算机工程与设计, 2014(3):750-754.

[7]Yu K, Dutkiewicz E. Improved Kalman filtering algorithms for mobile tracking in NLOS scenarios[C]∥Wireless Communications and Networking Conference (WCNC), 2012 IEEE. IEEE, 2012:2390-2394.

[8]耿剑, 张玲华. 一种基于修正卡尔曼滤波的蜂窝定位算法[J]. 数据采集与处理, 2013, 28(2):201-206.

[9]Lin C. Application of SDS-TWR technology in coal mine personnel positioning system[J]. Industry & Mine Automation, 2015.

[10]邱凤云. Kalman滤波理论及其在通信与信号处理中的应用[D]. 济南：山东大学, 2008.

[11]Sung W J, Lee S C, You K H. Ultra-precision positioning using adaptive fuzzy-Kalman filter observer[J]. Precision Engineering, 2010, 34(1):195-199.

[12]王聪伟. 基于扩展卡尔曼滤波的足式机器人运动速度估计研究[D]. 哈尔滨：哈尔滨工业大学, 2014.

[13]Wylile M P, Holtzman J. The non-line-of-sight problem in mobile location estimation[C]∥IEEE International Conference on Universal Personal Communications. 1996: 827-831.

Optimization Technology of Indoor Distance Measurement Based on CSS

WANG Jia-wei, WANG Jing-dong, ZHAO Qiang, WEI Xue-ying

(College of Automation Engineering, Nanjing University of Aeronautics & Astronautics, Nanjing 211106, China)

Abstract:Wireless ranging based on CSS (Chirp Spread Spectrum) is TOA (time of arrival) based ranging method, there are a lot of NLOS (Non-Line of Sight) error in the indoor environment, so the precision of ranging is low. For this reason this paper improve the traditional Kalman filter, add the NLOS error to the state vector, and use two step Kalman filter, to suppress the influence of NLOS error on ranging. Considering the coexistence of LOS(Line of Sight) and NLOS, this paper improve the two step Kalman filtering algorithm, improve the the NLOS error identification and filtering process in the second step filter, and apply to the ranging system. The experimental results show that with the range optimization method which is described in this paper, TOA ranging accuracy and anti-jamming capability have been significantly improved.

Key words:CSS; TOA; NLOS; Kalman filter

文章编号：1673-3819(2016)03-0131-05

收稿日期：2016-01-28

*基金项目：中央高校基本科研业务费专项资金(NZ2015202)

作者简介：王佳伟(1990-),男,福建长乐人,硕士研究生,研究方向为无线传感器网络。 王敬东(1966-),男,副教授。 魏雪迎(1993-)，女,硕士研究生。

中图分类号:TJ630.3+4；E917

文献标志码:A

DOI:10.3969/j.issn.1673-3819.2016.03.026

修回日期： 2016-02-29

赵强(1991-)，男,硕士研究生。