分流动单元平均毛管压力曲线归一化方法及应用
黄新波
(中国石化石油勘探开发研究院,北京 100083)
分流动单元平均毛管压力曲线归一化方法及应用
黄新波
(中国石化石油勘探开发研究院,北京 100083)
摘要:当油藏储层结构复杂、非均质性较强时,通过常规平均毛管压力得到的毛管压力曲线不能很好地反映油藏非均质性,因此引入流动单元聚类分析方法,对油田取心井目的层段岩样进行聚类分析,划分流动单元;将有毛管压力数据的每个岩样进行归类,运用 J 函数处理方法,得到不同流动单元平均化 J函数及平均毛管压力曲线。实例分析结果表明:分流动单元平均化毛管压力曲线能更好地反映油藏的非均质性,可用于计算油藏含水饱和度等参数,其结果精度较高。
关键词:流动单元;聚类分析;毛管压力曲线;J 函数
实验室能够测定油气藏特定岩心的毛管压力曲线,但是由于毛管压力曲线受渗透率、孔隙度等因素影响,具有不同渗透率和孔隙度的岩心毛管压力曲线是不同的,在整个油藏储层岩石孔隙结构特征研究和油藏数值模拟中,希望得到的是全油藏范围内不同物性参数下的毛管压力[1]。目前,为了消除渗透率和饱和度的影响,可以用J函数方法处理,得到油气藏平均J函数曲线,进而根据油藏实际的物性参数得到不同的毛管压力。
1流动带指标法划分流动单元
通过对Kozeny-Carman的孔渗关系式修改,可推导出划分流动单元的流动单元指数FZI。利用FZI提高渗透率的解释精度是目前国内外研究及应用较为广泛的方法[2-4],其表达式为:
(1)
(2)
(3)
式中:FZI——流动单元指数,μm;RQI——储层质量指数,μm;φz——孔隙体积φe与颗粒体积之比,无量纲;K——渗透率,10-3μm2。
具有相同FZI值的样品,具有相同的孔渗性质,属于同一类型流动单元。通过对众多样品的FZI值进行聚类分析,可对水力流动单元进行分类。对每类流动单元的电测响应进行多元回归,建立相应流动单元的预测模型,进而预测非取心井的流动单元。
2J函数计算饱和度方法介绍
岩石的毛管压力是岩石中流体饱和度的函数[5-6],可以表述为下式:
Pc=f(Sw)
(4)
式中:Pc——毛管压力,MPa;Sw——流体饱和度,%。
J函数表达式为:
(5)

计算饱和度方法如下:
(1)将实验室测得的毛管压力曲线转换为油藏条件下毛管压力曲线:
(6)
式中:Pc——毛管压力,bars;σ——界面张力,dyn/cm;θ——润湿接触角,(°);下标res表示油藏条件下测量值,lab表示实验室条件下测量值。
(2)对岩心毛管压力曲线进行J函数处理:
(7)
(3)对样品的J(Sw)和Swn进行回归[7],可以得到:
J(Swn)=a(Swn)b
lnJ(Swn)=lna+blnSwn
(8)
将得到的每条毛管压力曲线回归系数a、b值进行平均化[8](几何平均或算术平均),即得平均毛管压力曲线。
(9)
(4)已知油藏中任一点的高度,由式(10)计算该处毛管压力:
(10)
式中:H——自由水面以上的高度,m;ρw,res、ρo,res——油藏条件下水、油密度,g/cm3;Pc——毛管压力,0.1 MPa;再结合该高度的孔隙度和渗透率,由式(6)至式(10)可得:
Sw=Swi+(1+Swi)Swn
(11)
3实例应用
某海上E油田主力储层为Gamba砂岩和Dentale砂岩,储层之间为角度不整合接触。Gamba层为近海沉积,储层厚度5~40 m,埋深1 770~1 810 m。该储层物性极好,孔隙度0.3%~36.0%,平均25.0%;渗透率(0.2~11 200)×10-3μm2,平均1 020×10-3μm2。Dentale层为河流湖泊沉积,储层厚度20~160 m,埋深1 810~1 970 m。该储层物性较好,孔隙度6%~32%,平均18%;渗透率(0.1~530)×10-3μm2,平均52×10-3μm2。
对该区410个岩心样品进行流动单元聚类分析,划分6类流动单元,如图1、表1所示。

表1 流动单元划分标准
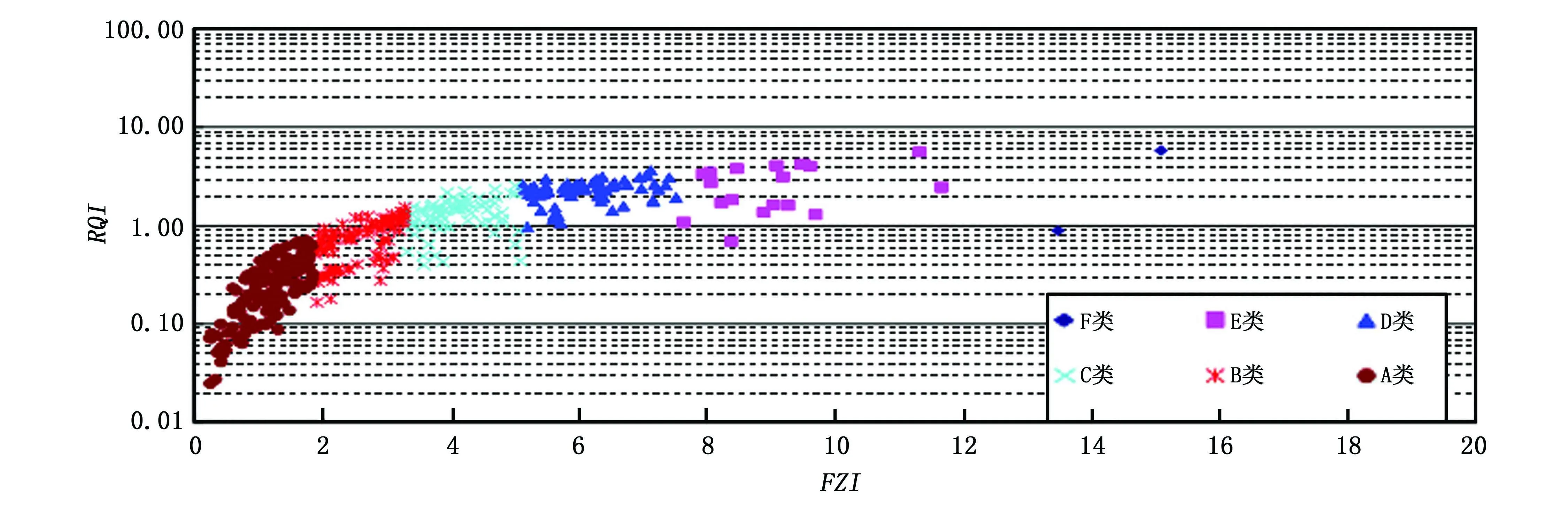
图1 RQI和FZI聚类结果
该油田15个岩心样品有实验数据见表2,依据流动单元划分标准对其进行归类,并对同一类型毛管压力曲线用J函数方法进行平均化,平均毛管压力公式回归数据见表3。
将表3中参数带入式(9),得到油藏不同流动单元平均化毛管压力曲线(图2)。从图中可以看出,C型、D型、E型和F型流动单元的孔渗结构依次变差。
将该结果在研究区用于计算含水饱和度,并与通过常规平均毛管压力得到的含水饱和度进行对比,见表4。由表4可以看出:旧方法计算的含水饱和度误差偏大,普遍大于10%;而采用本方法计算的含水饱和度误差在10%以内,明显优于旧方法的结果。
油藏不同区域流体间的界面张力、渗透率、孔隙度、束缚水饱和度是不同的。经过处理后,分流动单元平均毛管压力曲线更符合油藏实际,能使储层岩石孔隙结构特征研究和油藏模拟区域划分更加精细和准确。
4结论与建议
(1)将多块岩心的毛管压力曲线基于流动单元划分结果进行归类,得到不同流动单元平均毛管压力曲线及表达式,能更好地反映油藏的非均质性特点,为分区开展油藏数值模拟计算打下基础,也为毛管压力平均化提供了一种简单可行的新思路。

表2 15块岩心在不同压汞毛管压力下的驱替相饱和度
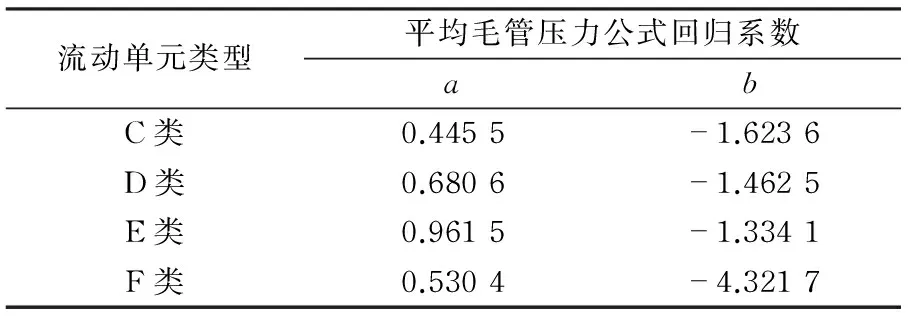
表3 不同流动单元下平均毛管压力公式

图2 E油田分流动单元平均毛管压力曲线

流动单元深度/m含水饱和度测量值/%旧方法含水饱和度/%误差/%新方法含水饱和度/%误差/%C类1772353911.432-8.6C类1781283317.9307.1D类1785414612.2422.4E类1791364011.133-8.3E类18045350-5.7589.4D类181355597.352-5.5F类18285751-10.555-3.5F类1835626911.3643.2
(2)根据公式(11)可以计算油藏中油层任一高度的含水饱和度。该方法考虑了岩石孔隙度、渗透率及含油气高度,不受地层岩性及所含矿物的影响,因而提高了毛管压力曲线的统计应用范围。当缺乏密闭取心资料,用电阻率测井资料解释含水饱和度遇到困难时,可以采用该方法。
参考文献
[1]陈杰, 周改英. 储层岩石空隙结构特征研究丰富综述[J].特种油气藏, 2005, 12(4): 13-14.
[2]Amaeful J O, Altunbay M, Tiab D, etc. Enhanced reservoir description using core and log data to identify hydraclic (flow) units and predict permeability in uncored interval wells[J].SPE 26436, 1993:103-110.
[3]李阳, 刘建民. 流动单元研究的原理和方法[M].北京: 地质出版社, 2005:80-90.
[4]窦之林. 储层流动单元研究[M].北京: 石油工业出版社, 2000:120-140.
[5]何更生. 油层物理[M].北京: 石油工业出版社, 2004: 192-215.
[6]李传亮. 油藏工程原理[M].北京: 石油工业出版社, 2006: 55-63.
[7]罗明高. 毛管压力曲线分布特征的确定[J].西南石油学院学报, 1988, 10(4):71-85.
[8]缪志伟. 一种计算平均毛管压力曲线的方法[J].新疆石油地质, 1997, 18(1):67-69.
编辑:赵川喜
文章编号:1673-8217(2016)03-0099-03
收稿日期:2015-11-10
作者简介:黄新波,硕士研究生,工程师,1980年生,2005年毕业于中国石油大学(北京)油气田开发专业,现从事油藏工程研究。
中图分类号:TE112.23
文献标识码:A

