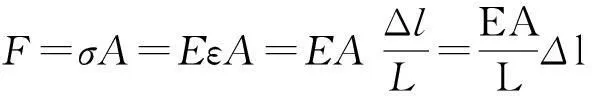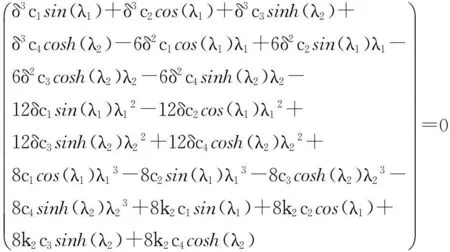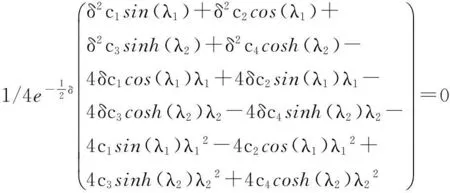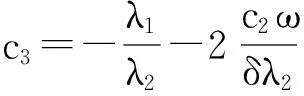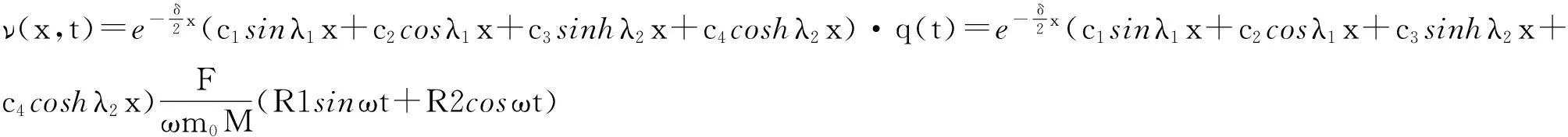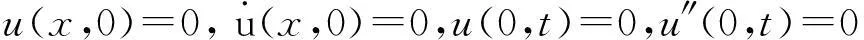变截面梁在移动荷载作用下的动力响应

梁耀哲，褚少辉，赵存宝，张　涛，张艳玲

(1.河北省建筑科学研究院，石家庄　050021；2.河北建研科技有限公司，石家庄　050021；3.石家庄铁道大学，石家庄　050043)

变截面梁在移动荷载作用下的动力响应

梁耀哲1，褚少辉2，赵存宝3，张涛2，张艳玲2

(1.河北省建筑科学研究院，石家庄050021；2.河北建研科技有限公司，石家庄050021；3.石家庄铁道大学，石家庄050043)

摘要：变截面梁具有等强度、质量分布优化等优异的力学性能，广泛应用在桥梁工程中。按照2种边界条件(两端固支、一端简支一端弹性支撑)，分别给出系统的控制方程，研究变截面梁承受移动荷载时的动力响应，并采用有限差分法对得到的精确理论解进行验证，分析相关参数。结果显示，两者吻合良好。

关键词：耦合振动;移动荷载;变截面桥梁

0引言

近些年来，随着人类社会的飞速发展和科学技术的不断进步，交通运输系统在规模和技术上都有了很大的提高。在各种交通系统(铁路、公路、地下铁道等)中，车辆运行速度不断加快，车流密度日益增加，车辆载重也逐渐加大。在这种情况下，车辆与桥梁的动力相互作用问题越来越受到人们的重视[1-3]。对车辆—桥梁动力相互作用系统进行综合研究，以便对桥梁的动力性能和桥梁上运行的车辆的走行性做出动力分析和评估，确定它们在各种状态下的使用可靠性，是合理进行铁路等工程设计的实际需要，对于承受移动荷载的交通土木工程结构物的设计和建造具有十分重要的理论和实际意义。

目前，国内外有大量等截面梁的研究与分析[4-5]，而对于变截面梁，国内外只有少量的数值模拟分析，理论解很少见。文献仅对两边简支梁在移动荷载作用下的响应进行了理论分析，其他边界条件尚需进一步研究。本文讨论了2种边界条件(两端固支、一端简支一端弹性支撑)，车辆经过变截面梁时的动力响应，并采用有限差分法进行了验证，在此基础上，又进行了一系列的参数分析，讨论了非均匀系数δ、车辆行驶速度c等参数变化对系统动力响应的影响。

2振动方程求解

现有一矩形变宽度截面梁，高度不变，宽度按照指数形式变化，即b(x)=b0eδx。其中：b0为初始宽度，δ为非均匀系数，梁横截面的高为常数h，长度为L，各截面的形心连成为一条直线，将x轴设在这条直线上。现有一车辆匀速驶过该桥，利用文献[6]中相关推导，得到其模态函数

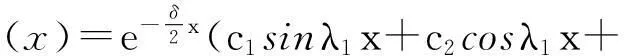
c3sinhλ2x+c4coshλ2x) ，

(1)

其中：

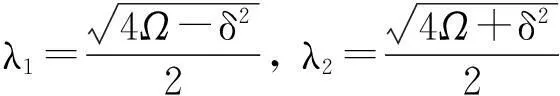
常数c1，c2，c3，c4由系统的边界条件确定。

该公式适合宽度按指数变化的等高度变截面均匀梁，集中力的形式可以多样。只要集中力只随时间变化且可以积分，边界条件就可以多样。下面将探讨两种边界条件(两端固支、一端简支一端弹性支撑)下桥梁的弯曲振动响应。

3两端固支梁弯曲振动响应

3.1理论解

两端固支梁的边界条件为：固定端处梁的挠度ν和转角∂ν/∂x均等于零。即

φ(0)=0, φ′(0)=0, φ(1)=0,φ′(1)=0

代入式(1)，得到关于c1、c2、c3、c4的一个四元一次线性方程组：

c2+c4=0,

(2)

e-1/2δ(c1sin(λ1)+c2cos(λ1)+c3sinh(λ2)+c4cosh(λ2))=0 ，

(3)

-1/2δc2-1/2δc4+c1λ1+c3λ2=0，

(4)

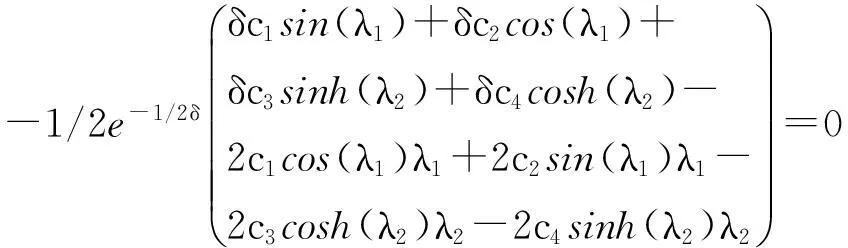
(5)

以上方程组有非零解的充要条件是系数矩阵A的行列式：|A|=0，此时方程组有无穷多解。为方便起见，可取其一组解。

c1=1,

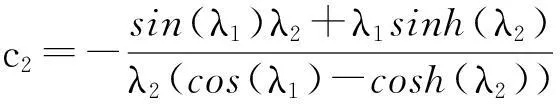
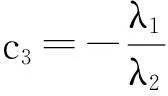
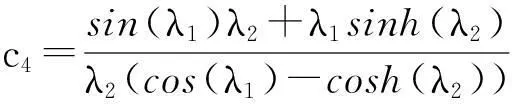
将c1，c2，c3，c4代入式(1)即可得到模态函数，进而求得系统响应方程：

(6)

3.2算例

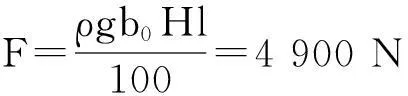
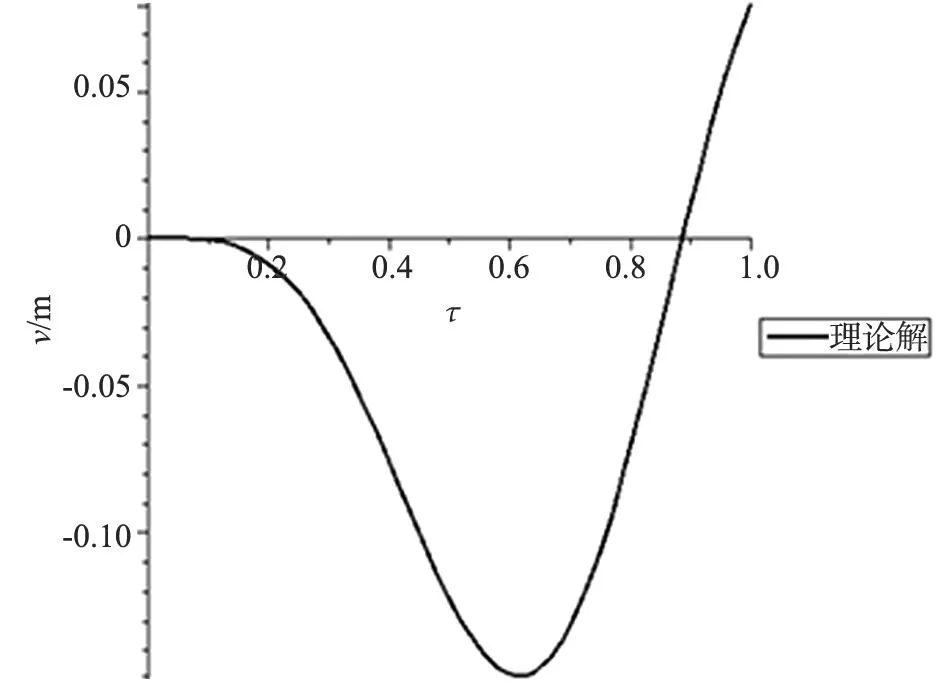
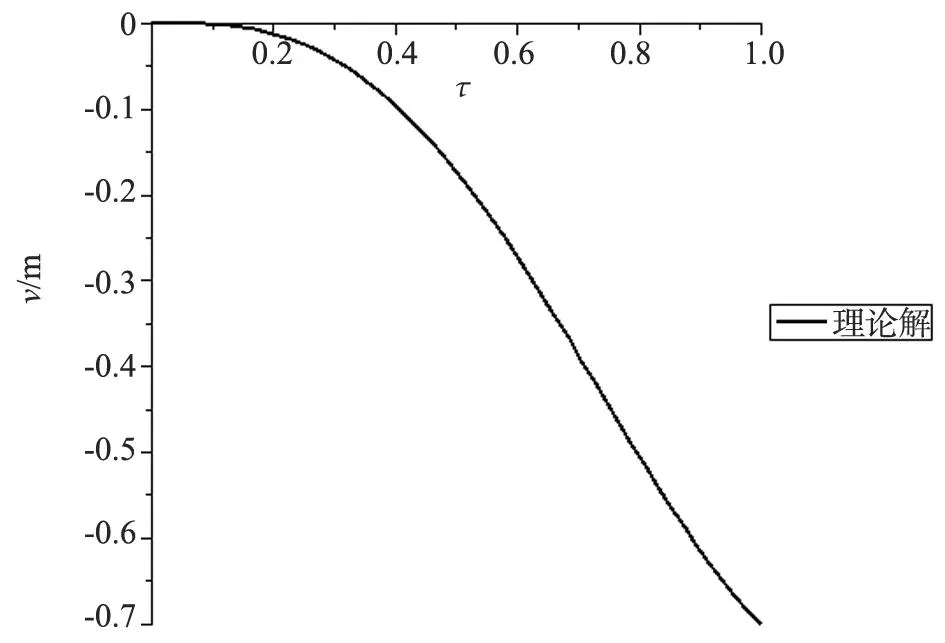
图1　c =4 m/s、δ=0.1两端固支梁跨中挠度时程曲线(理论解)

由图1可以看出，车速ν=4 m/s时，变截面梁在车通过桥面过程中，跨中挠度先增大后减小，在梁的0.6l处挠度最大，然后逐渐减小，在0.89l处减小到零，然后向反方向逐渐增大。从曲线趋势可以看出，反向最大值出现在车离开桥面后。

3.3有限差分法数值验证

根据文献[2]，系统的振动方程如下所示

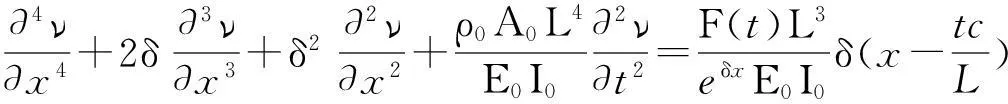
为便于比较，将上式化为x和τ的函数，以下为Maple中的结果：

(7)

式中的Dirac(x-τ)即为δ(x-tc/L)。将已知条件代入以上方程，已知条件为：

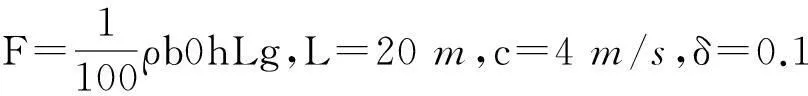
E=108Pa，

ρ=2.5×103kg/m3，h=0.5m，b0=2m。

于是，式(7)为

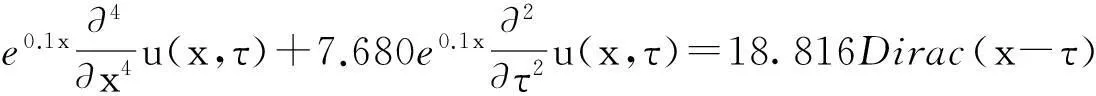
(8)

初始条件写为如下形式：

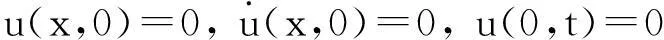
u′(0,t)=0, u(1,t)=0, u′(1,t)=0。

有限差分法根据所取项数的不同，其结果的精确程度会有差别。经调试，可以取前70项，同样做出跨中挠度时程曲线(图2)。

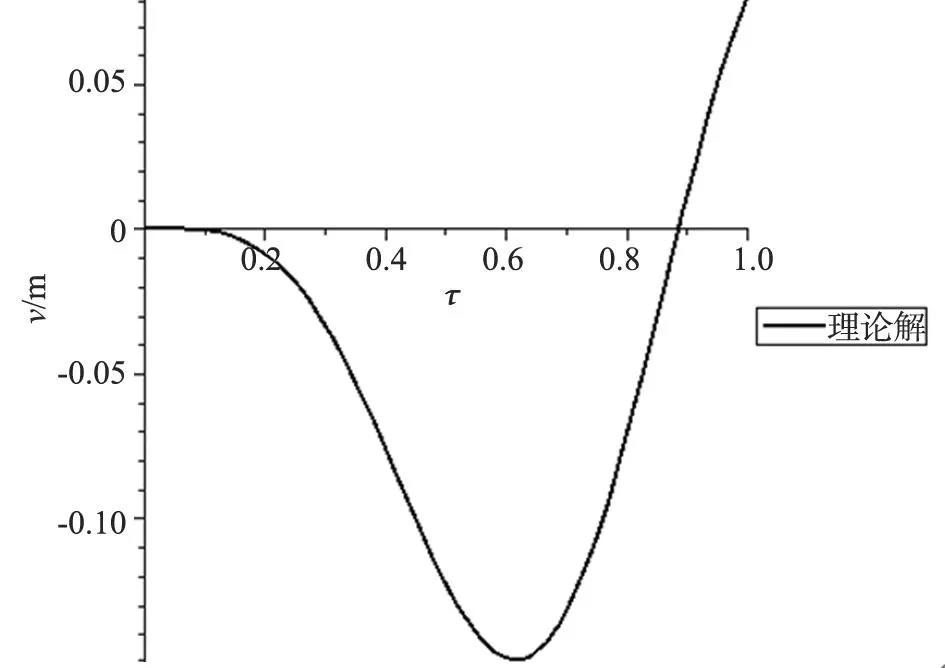
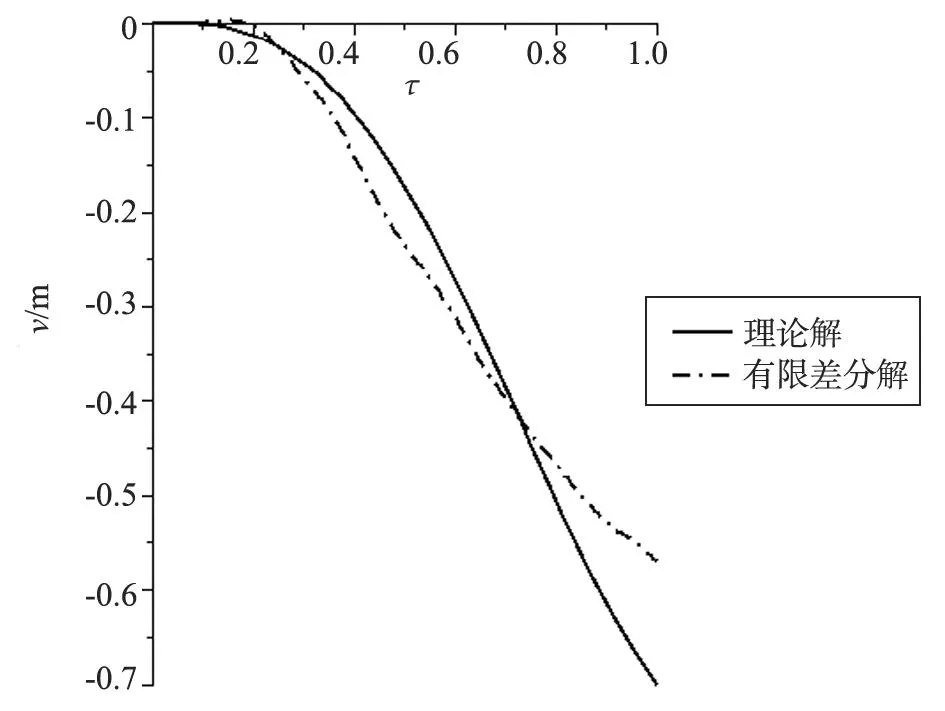
图2　c=4 m/s、δ=0.1跨中挠度时程曲线理论解与有限差分解对比

由图2可以看出，理论解与有限差分解几乎重合，两者计算结果一致。

3.4参数分析

由上文分析可知，本文推导理论解释是可靠的，现利用理论解分析梁的非均匀系数和车速变化对时程曲线的影响。

1)速度c不变，非均匀系数δ变化的情况(图3)。

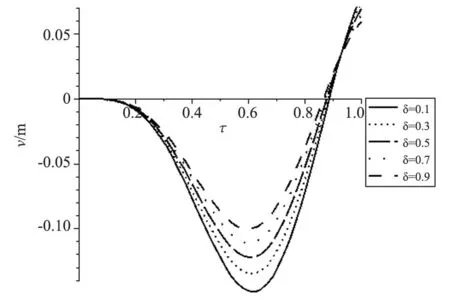
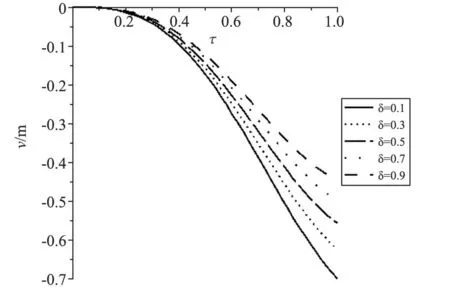
图3　c=4 m/s对应不同δ的跨中挠度时程曲线

由图3可知，随着非均匀系数δ的增大，时程曲线走势一致，跨中挠度最大值逐渐减小。

2)非均匀系数δ不变，速度c变化的情况(图4)。

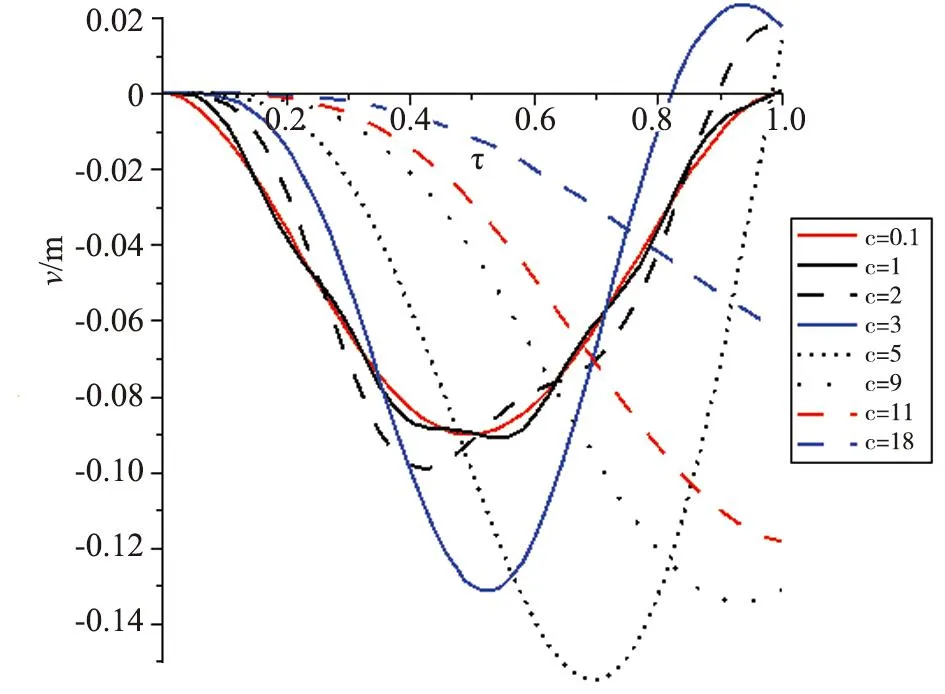
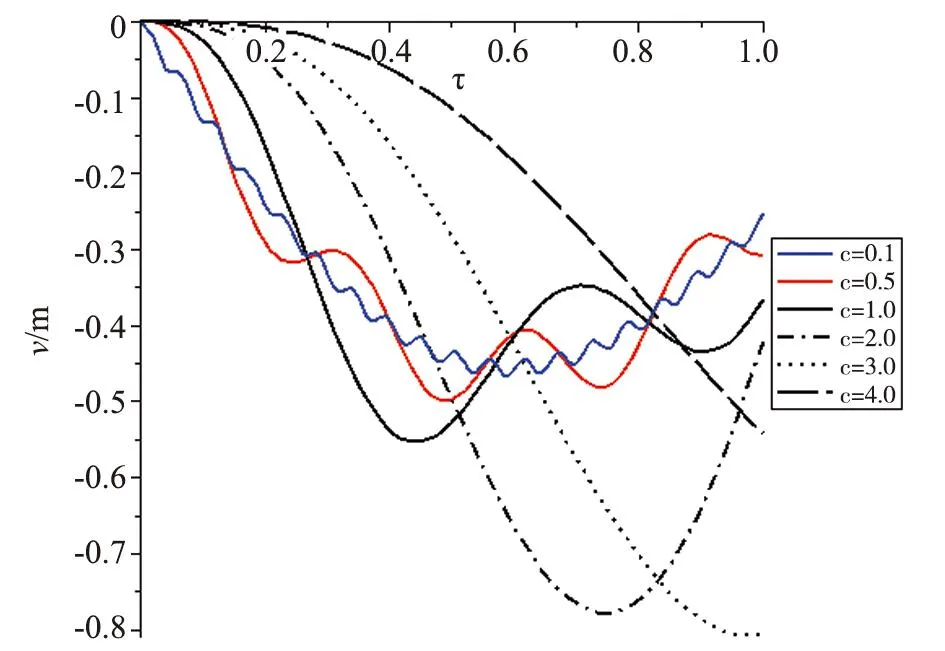
图4　δ=0.1对应不同速度c跨中挠度时程曲线

增大匀速移动的速度，车辆在桥面行驶过程中，跨中挠度最大值先增大后减小，最大值出现的时间节点也有所变化，当速度c<3 m/s时，最大值均出现在车辆行驶在中点位置时；当速度c>3 m/s后，最大值出现的时间逐渐后延；当速度c>11 m/s时，最大值出现在车辆离开桥面后；当2 m/s

4一端简支、一端弹性支承梁弯曲振动响应

4.1模型简化及理论解

将弹性支承简化为一压杆，杆端与梁端铰支，只限制梁端的竖向位移，而不影响其转角位移。引入相对弹性刚度k，计算如下：

一端简支、一端弹性支承的边界条件为：设梁的末端为弹性支承，弯矩M等于零，剪力与支座反力相等，简支端处梁的挠度ν和弯矩均等于零。

将φ(0)=0,φ″(0)=0,φ″(1)=0,EI(1)φ‴(1)=kφ(1)

代入式(1)，得到关于c1、c2、c3、c4的一个四元一次线性方程组：

c2+c4=0，

(9)

(10)

1/4δ2c2+1/4δ2c4-δc1λ2-δc3λ2-c2λ12+

c4λ22=0，

(11)

(12)

求解得：

c1=1 ，

c4=-c2。

将c1、c2、c3、c4代入式(1)，即可得到模态函数。

已经求得φ(x)，与前文推导一致，求出系统响应方程：

(13)

4.2算例

与3.1节相同算例，边界条件改为一端简支、一端弹性支撑，做出跨中挠度时程曲线(时间归一化)(图5)。

图5　c=4 m/s、δ=0.1两端简支梁跨中挠度时程曲线(理论解)

由图5可以看出，车速c=4 m/s时，变截面梁在车通过桥面过程中，跨中挠度逐渐增大，最大值出现在车辆离开桥面后。

4.3有限差分法数值验证

控制方程与3.3节相同，初始条件写为如下形式

u″(1,t)=0,u‴(1,t)=43.43u(1,t)

理论解和有限差分解作出图形如下所示，横轴为无量纲量。

图6　c=4 m/s、δ=0.1跨中挠度时程曲线理论解与有限差分解对比

由图6可以看出，理论解与有限差分解在车辆离开桥面前大致相同，离开桥面后，理论值将会偏大。因此，该理论解只适用于车辆离开桥面前的分析。

4.4参数分析

1)速度c不变，非均匀系数δ变化的情况(图7)。

图7　c=4 m/s对应不同δ的跨中挠度时程曲线

由图7可知，随着非均匀系数δ的增大，时程曲线走势一致，跨中挠度最大值逐渐减小。

2)非均匀系数δ不变，速度c变化的情况(图8)。

图8　δ=0.1对应不同速度c跨中挠度时程曲线

车辆在桥面行驶过程中，当速度c≤1 m/s时，跨中挠度出现了波浪式起伏变化，当速度c>1 m/s时，时程曲线变得平滑，最大值随着速度的增大逐渐增大，出现的时间节点也逐渐后延，当速度c>3 m/s时，最大值出现在车辆离开桥面后。

5结论

本文主要讨论了变截面梁的车桥耦合振动问题，在研究过程中，忽略了桥梁自身的质量，将移动车辆荷载简化为一个按时间变化的力，讨论了2种边界条件(两端固支、一端简支一端弹性支撑)变截面梁的动力响应。

1)详细地给出了系统响应方程推导计算过程，得出了理论解，并用有限差分法进行数值验证，两者吻合良好，说明本文推导的理论解是可靠的。

2)两端固支梁。车辆速度c保持不变，当非均匀系数δ逐渐增大时，跨中挠度的最大值逐渐减小，但是最大挠度均出现在相同的时间节点；非均匀系数δ保持不变，当车辆荷载行驶速度逐渐增大时，车辆在桥面行驶过程中，跨中挠度最大值先增大后减小，最大值出现的时间节点也有所变化。当速度c<3 m/s时，最大值都是出现在车辆行驶在中点位置时；当速度大于c>3 m/s后，最大值出现的时间逐渐后延；当速度c>11 m/s时，最大值出现在车辆离开桥面后；当2 m/s

3)一端简支、一端弹性支撑梁。车辆速度c保持不变，随着非均匀系数δ的增大，跨中挠度最大值逐渐减小，出现的时间节点也逐渐后延。非均匀系数δ保持不变，车辆在桥面行驶过程中，当速度c≤1 m/s时，跨中挠度出现了波浪式起伏变化；当速度c>1 m/s时，时程曲线变得平滑，最大值随着速度的增大逐渐增大，出现的时间节点也逐渐后延；当速度c>3 m/s时，最大值出现在车辆离开桥面后。

参考文献：

[1]邓学钧, 孙璐. 车辆-地面结构系统动力学[M]. 北京:人民交通出版社, 1998.

[2]翟婉明. 车辆—轨道耦合动力学[M]. 3版. 北京: 科学出版社, 2007.

[3]郭欢, 孙武强, 于洋, 等. 钢筋混凝土圆筒仓仓壁结构的地震反应分析[J]. 华北地震科学, 2016, 34(1): 53-58.

[4]张钧博. 公路桥梁的车桥耦合振动研究[D]. 成都: 西南交通大学, 2007.

[5]曹雪琴, 刘必胜, 吴鹏贤. 桥梁结构动力分析[M]. 北京: 中国铁道出版社, 1987.

[6]张洁, 褚少辉. 移动荷载作用下桥梁动力响应分析[J]. 华北地震科学, 2015, 33(2): 1-5.

Dynamic Response Analysis of Beams with Variable Cross-sections under Moving Loads

LIANG Yao-zhe1, CHU Shao-hui2, ZHAO Cun-bao3，ZHANG Tao2，ZHANG Yan-ling2

(1.Hebei Academy of Building Research, Shijiazhuang 050021, China;2.Hebei Architecture Research Technology co.ltd, Shijiazhuang 050021, China;3.Shijiazhuang Tiedao University, Shijiazhuang 050043, China)

Abstract:Beams with variable cross-sections show excellent mechanical properties, such as equal intensity, the optimization of mass distribution, and it has been widely used in bridge engineering. In the study, control equations of system vibration according to two types of boundary conditions (both of the two ends of the beam are clamped, one end of the beam is simply supported and the other is elastically supported) were given to study the dynamic responses of beams with variable cross-sections under move loads. Furthermore, the comparatively precise theoretical solutions were verified by the finite difference method. The result shows that the solutions are well consistent with that of the finite difference method.

Key words:coupled vibration; moving loads; beam with variable cross-section

收稿日期:2015-11-17

基金项目：河北省高等学校科学技术研究项目“垮塌深水大跨桥梁交通应急浮桥抢修技术研究”(ZD2015081)

作者简介：梁耀哲(1976—)，男，高级工程师，主要从事勘察、地基处理与基坑支护等岩土工作．E-mail:12533960@qq.com

中图分类号:P315.921;TU311.3

文献标志码:A

文章编号:1003-1375(2016)02-0057-06

doi:10.3969/j.issn.1003-1375.2016.02.010

梁耀哲,褚少辉,赵存宝，等．变截面梁在移动荷载作用下的动力响应[J]．华北地震科学，2016，34(2)：57-62.