基于振动声调制的金属微裂纹检测方法

方漂漂　郑慧峰　喻桑桑　竺科仪　王月兵　 曹文旭

1.中国计量学院，杭州，3100182.哈帝环保科技有限公司，杭州，310018

基于振动声调制的金属微裂纹检测方法

方漂漂1郑慧峰1喻桑桑1竺科仪2王月兵1曹文旭1

1.中国计量学院，杭州，3100182.哈帝环保科技有限公司，杭州，310018

摘要：为克服传统线性超声无法检测微纳级宽度裂纹的缺点，开展了振动声调制法检测金属微裂纹的研究。用有限元分析软件ABAQUS开展了仿真研究，并验证了该方法的有效性，为实验参数设置提供了参考。搭建振动声调制检测系统，分析了不同长度微裂纹的调制特性，提出了基于振动声调制信号的信息熵定量表征方法。结果表明，存在微裂纹的铝板的振动声调制信号中的旁瓣信号明显，且检测信号的信息熵随裂纹长度单调增大，可作为振动声调制法检测微裂纹长度的特征参数。

关键词：微裂纹；振动声调制；非线性超声；定量表征

0引言

常规超声检测法由于微裂纹的反射回波强度低、透射率高、衰减小等原因，对微裂纹不敏感[1]。国内外研究者发现，非线性超声检测法可以很好地检测闭合微裂纹、复合材料分层等材料内部的接触性缺陷。振动声调制是非线性超声检测方法中的一种，通过低频振动声波和高频超声波与微裂纹相互作用，可使两列声波产生非线性耦合。它对接触缺陷有较高的灵敏度，可以用于检测复杂结构零件和大型构件及其结构远端，所以正受到越来越多的关注[2]。

目前对振动声调制的研究还多限于调制信号的影响因素分析、检测结果信号处理以及损伤的定量表征，还没有建立统一的定量表征参数来对微裂纹进行损伤评价。比较常用的评价损伤的参数是旁瓣信号幅值和主频信号幅值，Aymerich等[3]利用一阶旁瓣信号幅值表征损伤程度，发现旁瓣信号幅值随着损伤程度增大而增大。但郑磊[4]通过研究发现，旁瓣信号幅值和主频信号幅值并不随着裂纹长度的增加而单调增大，因此旁瓣信号幅值和主频信号幅值不适合作为裂纹长度的定量表征参数。Duffour等[5]通过实验发现，旁瓣信号幅值与主频信号幅值之比和裂纹长度也不是单调相关的。Trochidis等[6]把基于ZAM算法得到的旁瓣信号和主频信号的幅值之比作为裂纹深度的评价参数，它比基于FFT算法的幅值比对裂纹深度变化更加敏感，但仍然不是单调相关的，在工程实际中难以作为定量表征特征。

因此，本文根据振动声调制的理论，结合有限元仿真分析结果，搭建了振动声调制检测系统。以铝板为检测对象，研究不同激励信号与不同长度裂纹之间的调制结果，实现了振动声调制检测技术对裂纹的有效检测，并研究了信息熵与裂纹长度之间的关系，为振动声调制的定量表征提供参考。

1振动声调制的检测原理

振动声调制的基本原理如图1所示[4]，在检测过程中，向被测材料同时输入高频(ω1)和低频(ω2)声波，如果材料中没有缺陷，则振动声调制信号为两列声波的线性叠加；如果存在缺陷，材料内部空间在两列声波作用下会发生不均匀现象，缺陷处的质点振动速度改变，从而引起波的传播速度发生畸变，产生以频率ω1±ω2为主的非线性调制信号。

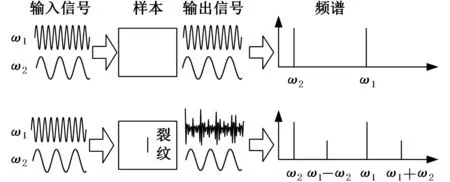
图1　振动声调制原理

为了更加具体地描述振动声调制，下面将通过公式推导来解释振动声调制的物理机理。

在一维条件下的各向同性体中，波动方程(保留二阶非线性项)为[2]

(1)

式中，c为波速；β为非线性系数；u为质点振动位移；x为传播距离；t为时间。

利用微扰近似理论，得到方程的近似解：

u(x,t)=u0(x,t)+βu1(x,t)

(2)

式中，u0为线性位移；u1为非线性位移。

暂不考虑衰减，则振动声调制信号的线性位移为

u0(x,t)=A1cosω1τ+A2cosω2τ

(3)

τ=t-x/c

式中，A1、A2分别为低频声波幅值和高频声波幅值。

假设非线性位移为

u1(x,t)=xh(τ)

(4)

式中，h(τ)为待定函数。

先将式(3)、式(4)代入式(2)，再代入式(1)，最后得到：

u(x,t)=u0(x,t)+βu1(x,t)=A1cosω1t+

βA1A2k1k2xsinω1tsinω2t/2

(5)

k1=ω1/c k2=ω2/c

从式(5)可以看出，两种信号与微缺陷相互作用，产生了二次谐波信号和旁瓣信号，并且旁瓣信号的幅值正比于非线性系数和基波信号幅值。

2有限元分析

为了给实验研究提供指导依据，先用ABAQUS软件对铝板进行振动声调制仿真，分析振动声调制超声非线性特性，验证振动声调制对微小裂纹检测的有效性。

2.1模态分析

根据Straka等[7]的研究，当振动信号频率选用铝板的模态频率时，振动声调制现象最明显，旁瓣信号幅值较大。所以用ABAQUS分别对尺寸为100mm×40mm，裂纹长度为0～20mm的铝板作模态分析。设置铝板密度为2700kg/m3，弹性模量为72GPa，泊松比为 0.35。为简化计算，采用二维平面模型，裂纹设在铝板模型中心，并使用线性摄动分析步，特征值求解器选择Lanczos，特征值数目设为30，模态分析结果如表1所示。

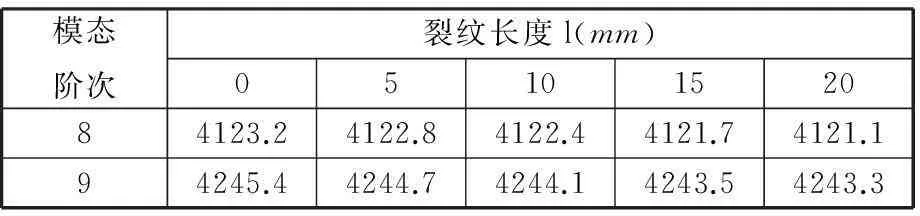
表1　模态分析结果(模态频率)　Hz

从表1可知：在相同模态阶次下，不同长度裂纹铝板的模态频率变化很小。所以下面对有无裂纹铝板的振动声调制仿真中，都选择相同的低频振动频率。有限元仿真时，为减小计算量，采用了二维平面模型，所以铝板模型的质量会比实际小，导致其固有频率比实际值偏大，但在同一阶次下模态分析结果的变化趋势并没有变化，所以仍然可以为实验操作提供参考。

2.2有限元建模及仿真

根据振动声调制原理，在铝板模型左端边界取2个点(高频信号和低频信号的输入点)，并施加正弦应力波，使材料内部质点产生振动，来模拟超声波的激励效果。由于裂纹在高低频应力波的共同作用下发生反复张开闭合，闭合的裂纹面将相互作用，所以需要将裂纹面定义为自接触，接触作用属性为法向硬接触。对于分析步设置，由于振动声调制是复杂非线性问题，所以选用显式动态分析。根据多次仿真经验以及ABAQUS作业管理器监控器输出的信息，把分析步总时间设为5 ms，固定增量步时间设置为5 ns。低频应力波频率设为4123 Hz，幅值为3 μm，高频应力波频率设为50 kHz，幅值为1.5 μm。仿真结果如图2、图3所示。

(a)时域图　　　　　　(b)频域图图2　无裂纹铝板仿真信号时域图与频谱图

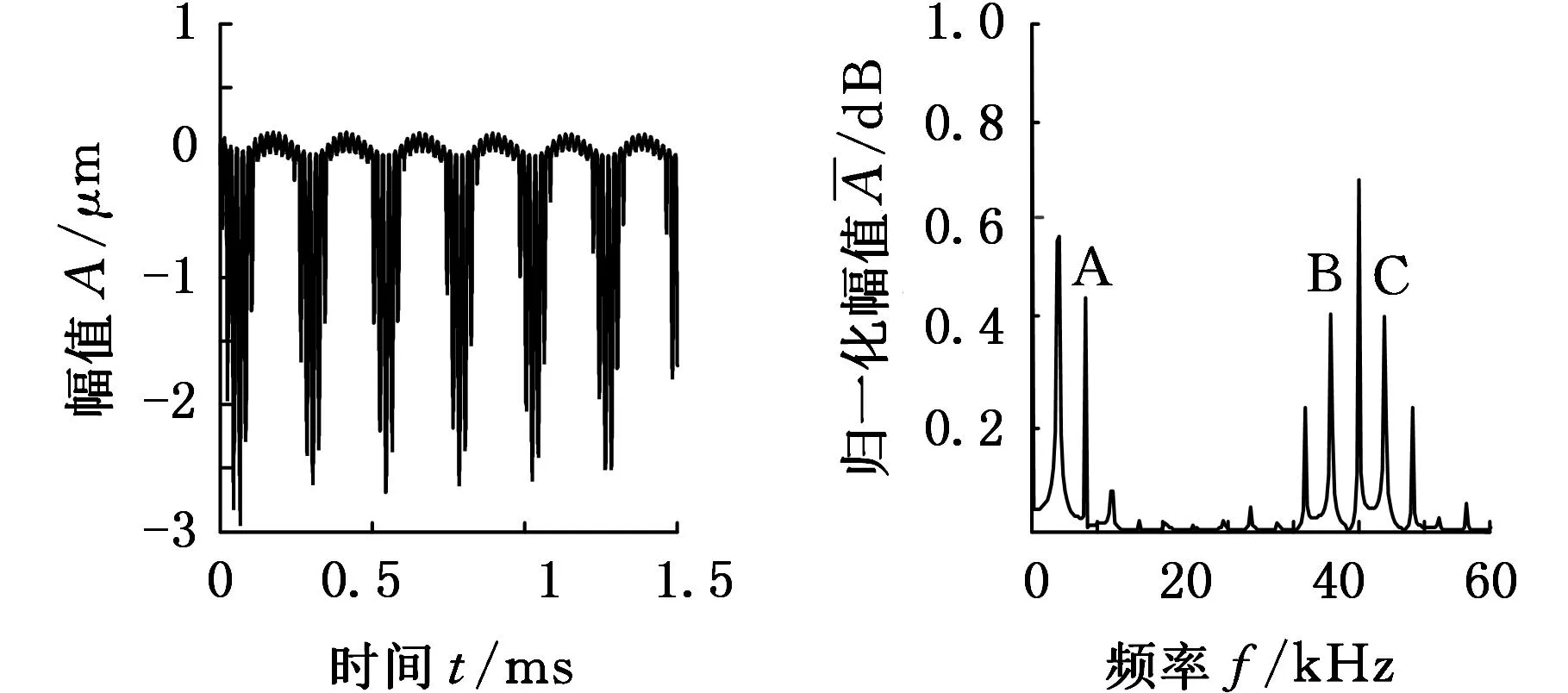
(a)时域图　　　　　　(b)频域图图3　有裂纹铝板仿真信号时域图与频谱图

从图2、图3可以看出：有缺陷铝板的时域信号相比于无缺陷铝板的时域信号，出现了明显的调制。从频域信号观察，当铝板中无缺陷时，高频信号周围未出现明显的旁瓣信号，但当材料中存在长为5 mm，宽为10 nm的微小裂纹时，在低频信号的倍频处出现了明显的二次谐波A，在高频信号周围出现了频率为(50 000±4123)Hz的旁瓣信号B、C。这与上文的振动声调制物理机理研究结果一致，表明振动声调制检测法可以对铝板中的微小缺陷进行有效检测。

2.3检测结果影响因素分析

对于振动声调制检测信号，调制现象越明显，旁瓣信号的幅值就越大，测量结果准确度越高。在仿真研究过程中发现，除了低频信号的频率会影响旁瓣信号的幅值外，基波信号幅值也会对旁瓣信号幅值有影响。

由式(5)可见，旁瓣信号幅值正比于非线性系数和基波信号幅值。高频信号幅值分别为1 μm、1.5 μm、2 μm，低频信号幅值从2 μm递增到5 μm，高频信号幅值、低频信号幅值与旁瓣信号幅值之间的关系如图4所示。其中低频信号频率为4123 Hz，高频信号频率为50 kHz。

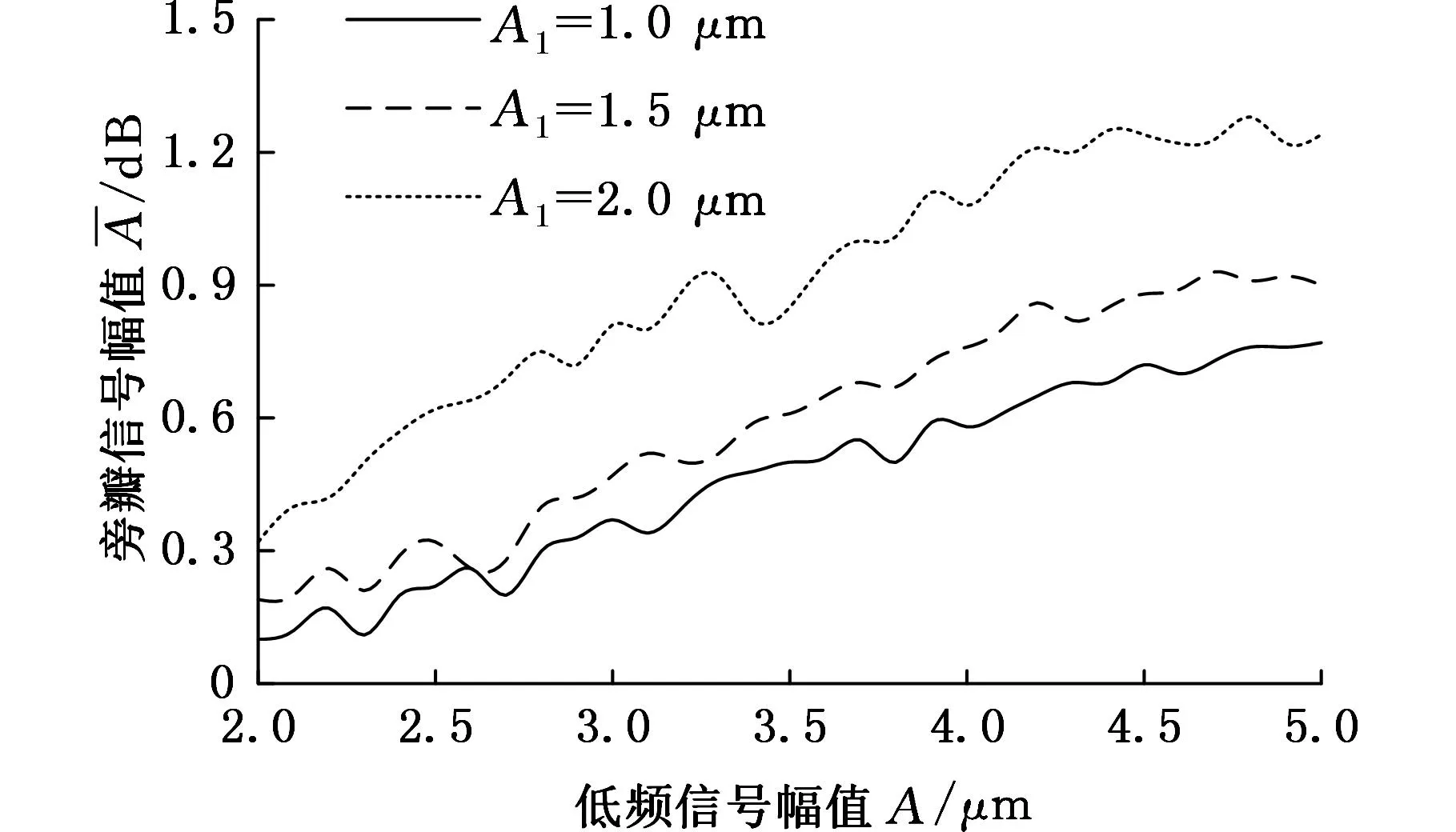
图4　低频信号幅值与旁瓣信号幅值关系(高频信号幅值为1 μm、1.5 μm、2 μm)

从图4可以看出：高频信号幅值越大，旁瓣信号幅值越大；旁瓣信号幅值与低频幅值成正比，但在低频信号幅值超过4.5 μm后增长变缓。所以可以选取较大的激励信号幅值,以获得更好的振动声调制检测效果。但同时要避免低频信号幅值过大导致铝板结构变形严重，使得振动声调制信号信噪比降低。

高频信号频率和接收信号采样位置同样会对检测结果有影响：高频信号的频率处于铝板的模态频率时，振动声调制效果最好，但其对结果的影响没有低频信号的影响明显；采样点和裂纹处于水平位置并且距离裂纹较近时，检测到的非线性特性最好。

3实验研究

振动声调制检测系统如图5所示，主要包括： 400 mm×200 mm×2 mm的薄铝板，φ25 mm×2 mm、中心频率为40 kHz的厚度伸缩型压电陶瓷片，信号发生器DG1022U、示波器DS2102、功率放大器JYH-200M及工控机等。利用信号发生器产生一路高频信号和一路低频信号，通过功率放大器放大后，将两路信号分别输入到2个压电陶瓷片产生超声激励和振动声激励，再由另1个压电陶瓷片接收振动声调制信号，最后由示波器采集传送给计算机进行数据处理并显示。

图5　振动声调制检测系统示意图

本实验中，需要疲劳实验机对铝板进行周期性加载，形成微裂纹，但因实验室设备有限，所以采用过盈配合的方式模拟微裂纹[8]。先在铝板中利用线切割加工一个公差等级为H6的圆形槽，然后在槽中塞入同样材料、公差等级为n5的塞片，把塞片与槽的接触面作为裂纹，如图 6所示，塞片的直径作为裂纹的长度。

图6　有裂纹铝板示意图

实验前，先要确定铝板的模态频率，用上述振动声调制检测系统对铝板模态进行测试，发现在1000～5000 Hz频率范围内存在两处振动幅值较大的频率(1200 Hz、3500 Hz)。通过仿真得知，在同一模态阶次下，裂纹对铝板的模态频率影响不大，所以可将无裂纹铝板的模态频率作为低频振动声信号的频率。

用振动声调制检测系统分别对无裂纹和裂纹长度为10 mm的铝板进行检测。由信号发生器、功率放大器和2个压电陶瓷片产生振动声激励和超声激励，其频率分别为1200 Hz和40 kHz，电压为100 V和50 V。再由压电陶瓷片接收振动声调制信号，并用示波器采集传送给计算机，得到图7、图8所示的振动声调制信号。

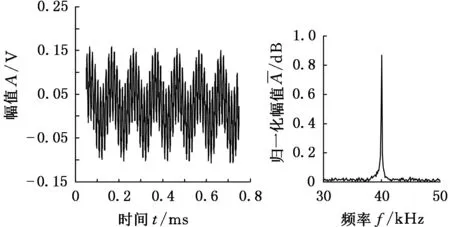
(a)时域图　　 　　　　(b)频域图图7　无裂纹铝板振动声调制信号

(a)时域图　　 　　　　(b)频域图图8　有裂纹铝板振动声调制信号

从图7、图8可以看出：无裂纹铝板的振动声调制信号没有明显的旁瓣信号，有微裂纹铝板的检测结果中出现了非常明显的一阶旁瓣信号(频率为(40±1.2)kHz)和二阶旁瓣信号(频率为(40±2.4)kHz)，二阶旁瓣信号幅值小于一阶旁瓣信号幅值。所以，可以根据有无旁瓣信号产生来定性判断是否存在裂纹，但还不能对裂纹的尺寸进行定量评价。

4微裂纹的定量表征方法

裂纹尺寸的定量表征一直是研究难题，由于振动声调制物理机理复杂，所以一直没有确定统一的表征参数[9]。信息熵可以用来描述信号的不规则度和复杂性，系统的混沌程度和复杂程度越大，熵值越大。一般故障信号和非故障信号相比，故障信号的复杂度较大，所以可以利用信息熵进行诊断[10]。如果概率分布p(xi)(i=1，2，…，n)，记为p1、p2、…、pn，则熵函数为

(6)

其中，底数B取不同值，信息熵有不同的量纲。B=2时，量纲为bit(比特)；B=e时，量纲为nat(纳特)，本文取B=e。

通过经验模式分解(Empiricalmodedecomposition，EMD)方法把有裂纹铝板振动声调制时域信号分解为8个固有模态函数(intrinsicmodefunction，IMF)，如图9所示。然后把所得的IMF1分量作Hilbert变换得到其瞬时频率和瞬时幅值，如图10所示。从图10可以看出：瞬时幅值随着时间周期性变化，瞬时频率以频率40kHz为中心上下跳动，说明振动声调制中存在频率和幅值两种调制。在有裂纹的铝板中，裂纹与两列声波发生频率和幅值调制，会增加振动声调制信号的复杂程度，所以熵值会比无裂纹的铝板的调制信号大。因此，在振动声调制中可利用信息熵进行损伤判断。

图9　振动声调制信号EMD分解结果

(a)瞬时幅值　　 　　　　(b)瞬时频率图10　有裂纹铝板振动声调制信号瞬时幅值、瞬时频率

为了研究信息熵能否对裂纹长度进行定量表征，在保持其他参数不变的情况下，使振动声激励电压分别为50 V、70 V、100 V，用振动声调制系统对裂纹长度为0～15 mm的铝板进行检测。然后对所得的振动声调制检测信号频域进行采样，并计算采样数组的概率分布，再代入式(6)求取熵值，得到的结果如图11所示。从图11可知：在不同电压的低频振动声激励下，调制信号的信息熵都随着裂纹长度的增加而线性单调增大；低频动信号幅值越大，振动声调制现象越明显，所以在同样裂纹长度下，随着低频振动信号幅值的增大，信息熵也增大。

图11　信号熵值与裂纹长度的关系

为了验证这种关系的正确性，在低频信号的频率1200 Hz、电压100 V，高频信号的频率40 kHz、电压50 V情况下，对裂纹长度为2 mm、5 mm、8 mm、11 mm、14 mm的铝板分别进行振动声调制检测，经计算得到信息熵，如表2所示。根据图11的拟合直线，查询到对应的裂纹长度，经计算可得所测数据的相对测量误差均小于3%。因此，可利用信息熵对裂纹长度进行定量评估。

表2　信息熵对裂纹长度的定量表征结果

5结论

(1)本文通过公式推导分析了振动声调制法检测微裂纹的机理，发现振动声调制信号中会出现正比于材料非线性的谐波信号，并通过有限元分析软件ABAQUS验证了该方法的有效性。

(2)搭建了一套振动声调制检测系统，对铝板中的微小裂纹进行了检测，分析其调制特性。研究发现，裂纹的存在会增加信号的复杂程度。因此，可将调制信号的信息熵作为损伤评价指标。

参考文献：

[1]吴斌，颜丙生，李佳锐，等.镁合金疲劳早期非线性超声在线检测实验研究[J].声学学报，2011，36(5)：527-533.

Wu Bin，Yan Binsheng，Li Jiarui，et al.Experimental Study of Early Fatigue Damage Online Measurement in Magnesium Using Nonlinear Ultrasonic[J].Acta Acustica，2011，36(5)：527-533.

[2]胡海峰.板状金属结构健康监测的非线性超声理论与关键技术研究[D].长沙：国防科学技术大学，2011.

[3]Aymerich F，Staszewski W J.Impact Damage Detection in Composite Laminates Using Nonlinear Acoustics[J].Composites Part A：Applied Science and Manufacturing，2010，41(9)：1084-1092.

[4]郑磊.管道闭合裂纹振动声调制检测方法研究[D].北京：北京工业大学，2012.

[5]Duffour P，Morbidini M，Cawley P.Comparison between a Type of Vibro-acoustic modelat Ion and Damping Measurement as ND Techniques[J].NDT & E International，2006，39(2)：123-131.

[6]Trochidis A，Hadjileontiadis L，Zacharias K. Analysis of Vibroacoustic Modulations for Crack Detection：a Time-frequency Approach Based on Zhao-Atlas-Marks Distribution[J].Shock and Vibration，2014，2014(10)：1-8.

[7]Straka L，Yagodzinskyy Y，Landa M. Detection of Structural Damage of Aluminum Alloy 6082 Using Elastic Wave Modulation Spectroscopy[J].NDT & E International，2008，41(7)：554-563.

[8]Tirosh J，Catz E.Mixed-mode Fracture Angle and Fracture Locus of Materials Subjected to Compressive Loading[J].Engineering Fracture Mechanics，1981，14(1)：27-38.

[9]Gurbatov S N，Rudenko O V，Saichev A L，et al.Waves and Structures in Nonlinear Nondispersive Media[M].Beijing：Higher Education Press，2011.

[10]刘国华，吴志根.引入信息熵理论的砼结构损伤动力识别新思路[J].振动与冲击，2011，30(6)：162-171.

Liu Guohua，Wu Zhigen.New Thought on Dynamic Identification Technology for Damage Detection of RC Structures by Introducing Information Entropy Theory[J].Journal of Vibration and Shock，2011，30(6)：162-171.

(编辑张洋)

Metal Micro Crack Detection Based on Vibro-acoustic Modulation Method

Fang Piaopiao1Zheng Huifeng1Yu Sangsang1Zhu Keyi2Wang Yuebing1Cao Wenxu1

1.China Jiliang University, Hangzhou, 310018 2.Hadi Environmental Protection Technology Company, Hangzhou, 310018

Abstract:In order to overcome the shortages that traditional linear ultrasonic testing could not detect the micro-cracks, VAM was studied. The VAM was simulated with finite element software ABAQUS to demonstrate the validity of the proposed method. The parameter setting of experimental testing system was also depended on the simulation results. VAM experimental testing system was established to investigate the nonlinear characteristic for micro cracks with variable lengths, and a quantitative characterization method was proposed based on information entropy of modulation signals. The results show that side-band signals are obvious when there is a micro crack in aluminum plate. The information entropy of modulation signals increases monotonically with increasing micro crack lengths and can be used as the characteristic parameter of crack length using VAM method.

Key words:micro crack；vibro-acoustic modulation (VAM)； nonlinear ultrasonic； quantitative characterization

收稿日期：2015-06-17

基金项目：国家自然科学基金资助项目(11474259)；浙江省自然科学基金资助项目(LY14E050013，LY15E050012)；浙江省公益技术应用研究项目(2014C31109)；浙江省“仪器科学与技术”重中之重学科开放基金资助项目；工程车辆安全性设计与可靠性技术湖南省重点实验室资金资助项目(KF1601)

中图分类号：TB523

DOI：10.3969/j.issn.1004-132X.2016.11.015

作者简介：方漂漂，女，1991年生。中国计量学院计量测试工程学院硕士研究生。主要研究方向为超声无损检测。郑慧峰，男，1981年生。中国计量学院计量测试工程学院副教授。喻桑桑，女，1989年生。中国计量学院计量测试工程学院硕士研究生。竺科仪，男，1981年生。哈帝环保科技有限公司工程师。王月兵，男，1963年生。中国计量学院计量测试工程学院教授。曹文旭，女，1991年生。中国计量学院计量测试工程学院硕士研究生。