基于优化信噪比算法的航空发动机振动信号分离

滕光蓉，李舜酩，梁恩波，王艳丰（.中国燃气涡轮研究院，四川江油6700；.南京航空航天大学，南京006）



基于优化信噪比算法的航空发动机振动信号分离

滕光蓉1，李舜酩2，梁恩波1，王艳丰1
（1.中国燃气涡轮研究院，四川江油621700；2.南京航空航天大学，南京210016）

摘要：为克服噪声对航空发动机振动信号的影响，提出一种优化信噪比的航空发动机振动信号分离方法，其通过建立时延自相关目标函数，对最大信噪比盲源分离算法进行优化。利用该方法，对航空发动机仿真混叠振动信号进行分析，分离后的信号频谱与源信号一致；对具有故障的实测航空发动机振动信号进行分离，成功分离出不同故障的振动特征。本文提出的方法为航空发动机振动信号的监测和故障诊断，提供了一种新的思路。

关键词：航空发动机；信噪比；时延自相关；盲源分离；混叠振动信号；故障诊断

Separation（BSS）；mixed vibration signals；fault diagnosis

1　引言

航空发动机试车过程中，受安装条件限制，振动传感器无法直接安装于转子和传动系统上，只能安装在外机匣上，以致传感器获取的不是单纯的源信号，而是高、低压转子振动与环境噪声等信号源的混叠信号［1］。在航空发动机振动信号分析过程中，从混叠振动信号中准确提取出原始振源信号，对找出真正的安全隐患具有极其重要的作用。

盲源分离（BSS）是近年来迅速发展起来的信号处理方法，在多个领域得到广泛应用［2-7］，受到国内外专家的青睐。国内李舜酩等［8-11］对盲源分离技术应用于航空发动机混叠振动信号分离做了大量研究，如应用基于峭度的快速独立分量分析算法，成功分离了多混叠转子振动信号；通过基于分离矩阵的加速度算法，实现多故障转子振动信号的分离；通过基于二阶非平稳盲源分离算法，清楚地反映了转子振动信号的频谱；通过基于负熵的快速分离算法，成功实现了转子复杂振动信号的盲分离。但目前国内在该领域还处于探索阶段，需要探索更多适合航空发动机振动信号分析的算法。

本文根据航空发动机振动信号的特征，采用优化最大信噪比（SNR）算法，对航空发动机仿真和实测振动信号进行盲源分离。

2　盲源分离基本原理

2.1盲源分离的概念

盲源分离是在不知道源信号和传输通道参数的情况下，根据输入信号的先验知识，仅由观测信号恢复出源信号各个独立成分的一种信号处理方法，其原理如图1所示。假定M个源信号s（t）= ［s1（t），…，sM（t）］T，N个传感器测得的观测信号x（t）= ［x1（t），…，xN（t）］T是M个源信号的线性组合，用矩阵的形式可表示为：

式中：A是N×M的常数混合矩阵。盲源分离的关键就是找一个分离矩阵W，使得x（t）通过W的混合信号y（t）是源信号s（t）的最佳估计，即：

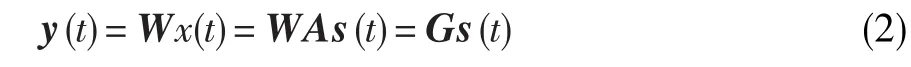
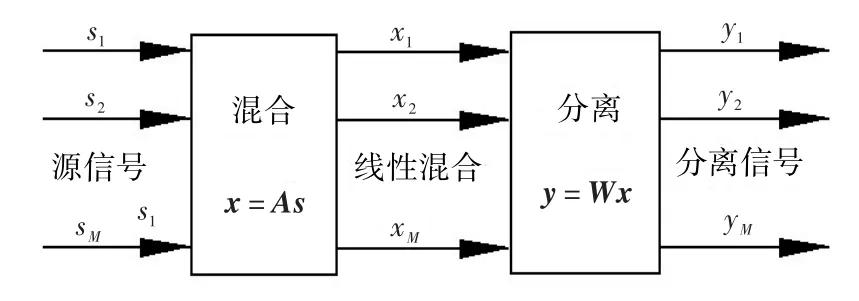
图1 盲源分离原理图Fig.1 Blind source separation principle diagram

2.2盲源分离的基本假设

仅由观测信号对源信号进行估计，将导致分离结果的多解性。为使盲源分离具有实际意义，必须作以下基本假设：

（1）源信号s（t）各分量之间统计独立，且最多只能有一个高斯分布源信号——两个高斯信号不能盲分离［12］。

（2）源信号个数等于观测信号数目（即M = N），且混合矩阵A是一个列满秩，即rank（A）= M［2］。

2.3盲源分离的两个不确定性

（1）尽管可以将源信号分离，但分离过程中很可能改变其排列顺序，即排列顺序的不确定性。

（2）分离后的信号往往幅值会改变，即信号幅值的不确定性。

因为振动源的大量信息蕴含在源信号的波形中，而不是蕴含在信号的振幅或系统输出的排列顺序中，所以盲源分离的两个不确定性并不影响盲源分离在机械状态监测与故障诊断中的应用。

3　优化最大信噪比算法

最大信噪比算法［13］的基本思想是通过建立信噪比目标函数，把求解过程转化为广义特征值的求法，用求出的广义值构成特征向量矩阵——分离矩阵。

建立性噪比目标函数前，可对目标信号进行优化处理（如滤波、自相关、时域平均等），以提高信噪比。因混叠在航空发动机中的噪声信号能量较大，且与转子振动信号之间存在一定的关联性，一般的优化方法难以对混噪的振动信号进行降噪。然而噪声信号在时延为零时具有最大的自相关值，自相关函数随着时延的增大很快衰减并趋于零。根据该特点，可将自相关函数用于机械振动信号的降噪中，从而保留振动信号中周期性的有用信号，有效去除随机非周期高斯白噪声，达到显著的降噪效果。因此，本文采用时延自相关降噪法对信噪比目标函数进行优化处理，然后利用优化后的信噪比目标求解分离矩阵。

3.1目标数据优化处理

对于含噪信号x（t），其自相关函数可通过式（3）求取。

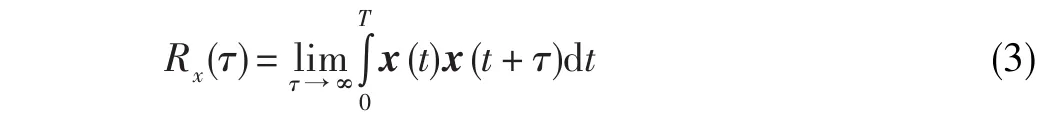
式中：τ为自相关函数时延，T为时间跨度值。从式（3）可知，周期性信号的自相关函数与原信号同周期。信号中的周期性分量在相应函数中不会衰减，保持原来周期。由于信号与信号自身相关，与噪声不相关，而噪声之间一般不相关，并随着时延的增大趋于零。因此，可通过信号的自相关方法对原始信号进行降噪处理。

3.2信噪比目标函数的建立

根据式（2）把源信号s（t）与估计信号y（t）的误差e（t）= s（t）- y（t）作为噪声信号。根据信噪比定义有：

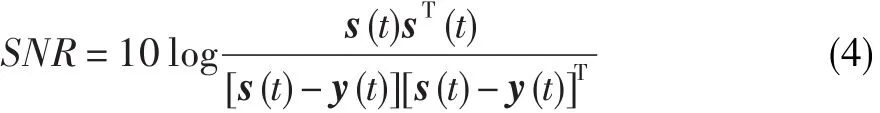
由于源信号s（t）未知，而估计信号又含有噪声，用估计信号y（t）的滑动平均（t）代替源信号s（t），并且为简化计算，将分子中的（t）用y（t）代替，因此最大信噪比目标函数可表示为：

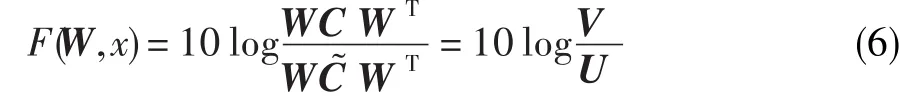
对式（6）两边的W求梯度得：

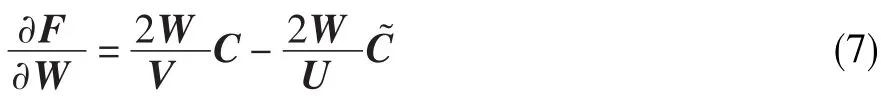
求解上式可得分离矩阵W。

3.3算法的可分离性

式（8）中的解是C~⋅C-1的特征向量，所以W中的列向量必与矩阵C和C-1正交，即

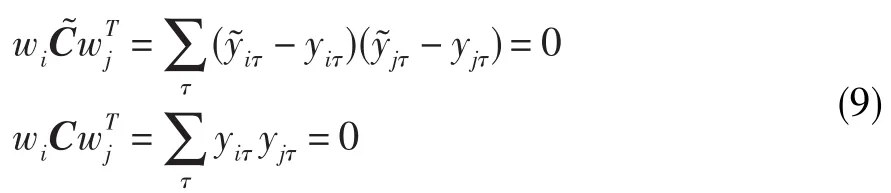
式中：w为W的元素。

式（10）说明，只要分离出的信号yi= wix和信号yj= wjx不相关，且其导数yi′= wix′和yj′= wjx′也不相关时，算法可解。由于yi和yj统计独立，满足算法可解的条件，因此式（9）保证了分离的可行性。

4　仿真分析

4.1仿真结果

航空发动机的振动信号，可看成由转子振动信号和其他振源信号线性瞬时混叠后与噪声信号混叠而成。转子振动信号又可视为由各自转频和各转频谐波频率的正弦信号叠加表示。

根据航空发动机振动信号的构成特征，由计算机生成两个仿真的航空发动机振动信号s1和s2，其中一个基频为10 Hz，另一个为17 Hz。两个信号分别包含基频及2倍、3倍频，信号采样点为16 384个，采样频率为200 Hz。为了能清楚对比各信号，取信号的前2 048个点，在没有噪声信号下的频谱如图2所示，其中上图为s1，下图为s2。

分别对信号s1和s2添加随机噪声，再分别对两个含噪信号进行混合。混合矩阵A=由计算机随机生成，得到的混合信号时域波形见图3，幅值谱见图4。从图4可看出，图中两信号都存在10 Hz基频及倍频成分，原信号s2中的17 Hz频率成分几乎观察不到，且两信号非常相似，几乎无法区分。由此可知：含噪声源信号混叠后，几乎无法获取原本信号的有效频率特征。因此，在工程应用中有必要对混合信号进行分离处理，以获取有效的振动特征信息。

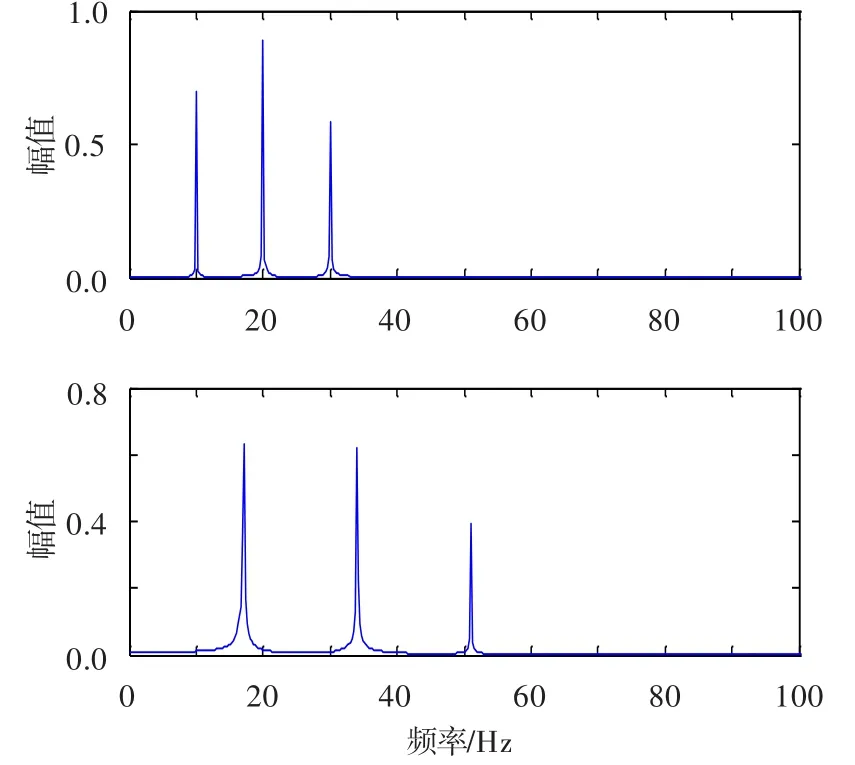
图2 无噪信号的幅值谱（仿真信号）Fig.2 The amplitude spectrum of the signal without noise （simulated）

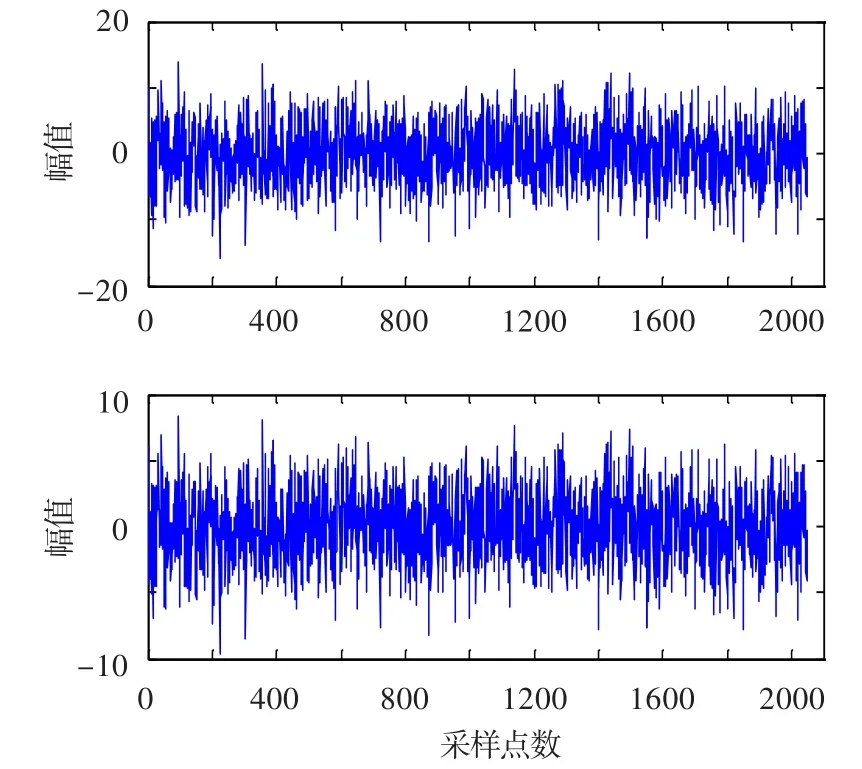
图3 含噪混合信号的时域波形图（仿真信号）Fig.3 Noise mixed signal waveform in time domain（simulated）

首先，直接对两个含噪混合信号用最大信噪比算法进行分离，分离结果如图5、图6所示。从图6可看出，尽管分离后信号排列顺序发生了改变，但10 Hz、17 Hz及其倍频信号基本得到分离；但相对于有效信号，频谱中仍包含较多强噪声，部分谱线仍被噪声淹没。

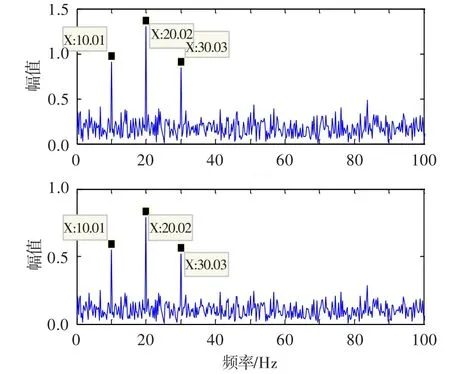
图4 含噪混合信号的幅值谱（仿真信号）Fig.4 The amplitude spectrum of the noise mixed signal （simulated）

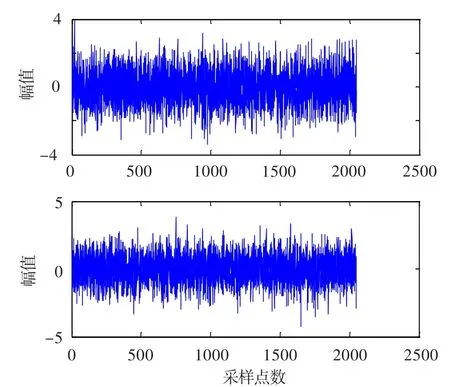
图5 直接分离后的信号时域波形图（仿真信号）Fig.5 Signals in time domain graph after direct separation （simulated）

图6 直接分离后的信号幅值谱（仿真信号）Fig.6 Signal spectrum amplitude after direct separation （simulated）

在进行最大信噪比分离之前，对原始混合信号进行时延自相关降噪优化处理，经优化最大信噪比分离后的信号处理结果如图7所示。结果显示：10 Hz、17 Hz及其倍频成分明显，相对有效信号，噪声信号大幅降低，原始混合信号得到有效分离。

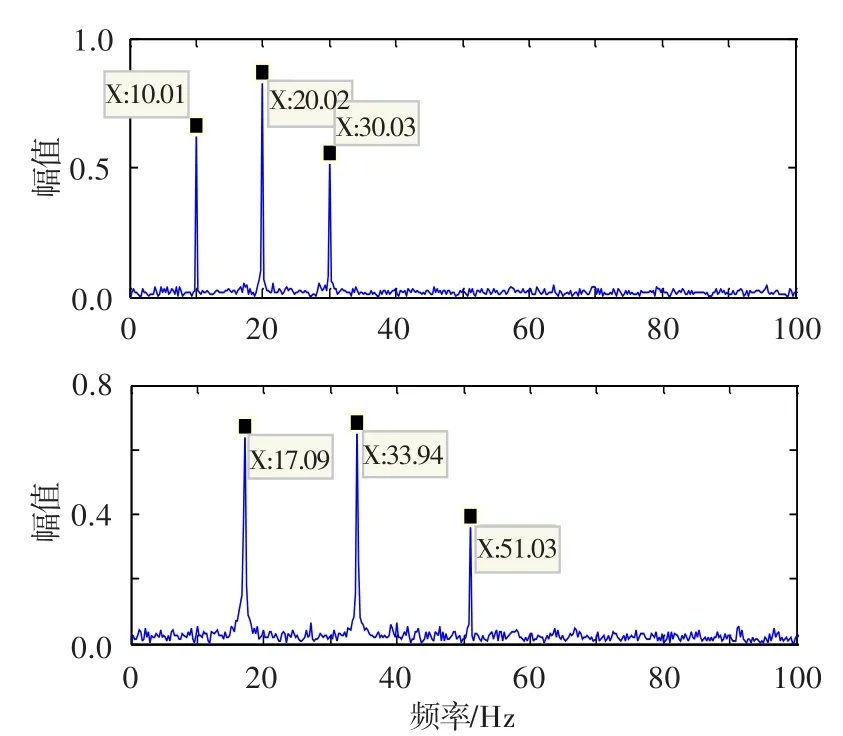
图7 优化处理后的分离信号幅值谱（仿真信号）Fig.7 Optimized signal amplitude spectrum（simulated）

4.2发动机实测混叠振动信号分析

某型航空发动机为单转子发动机，振动传感器安装在发动机涡轮机匣垂直、水平截面及压气机垂直截面上（图8）。发动机完成慢车至最大转速状态试车后检查发现，部分涡轮叶片叶根部位出现裂纹，叶尖存在掉块。发动机试车最大状态时物理转速为14 680 r/min（对应频率243.8 Hz）。截取发动机故障状态时的振动数据作为研究对象进行分析，其数据采样频率为12.8 kHz/s。任意选取2 048个采样点，其振动信号的时域波形和幅值谱分别如图9、图10所示。从图10可知，三个测点的传感器信号都受到了噪声影响，振源信号被强噪声淹没。

图8 航空发动机结构示意图Fig.8 Aero-engine structure

直接采用最大信噪比算法对振动信号进行分离，结果见图11和图12。图11中显示，所有测点受噪声影响，直接分离效果不明显，且各频谱相互混叠，难以识别各频率由何振源产生，对故障诊断的准确率造成很大影响。从图12可看出，直接分离后信号的幅值谱比FFT的幅值谱清晰，但信号中仍含有较多噪声，相对于噪声信号源信号幅值并不突出，且幅值谱仍存在混叠。

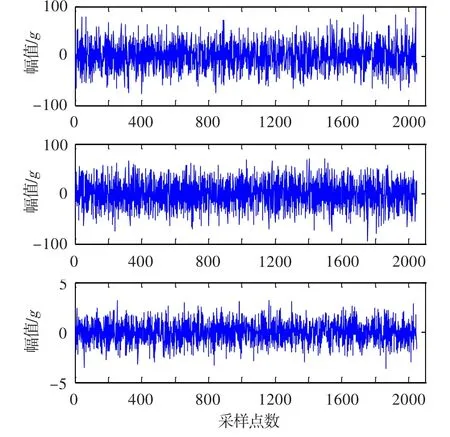
图9 振动信号的时域波形图（实测信号）Fig.9 Vibration signal time-domain waveform（actual measurement）

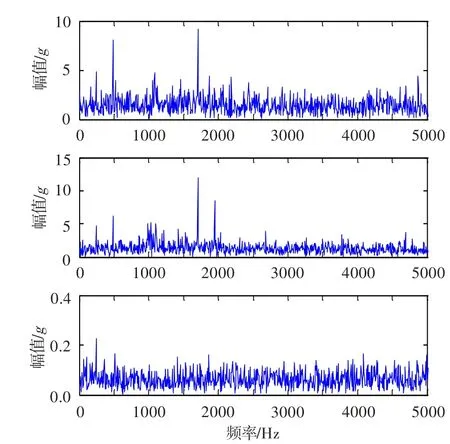
图10 振动信号的幅值谱（实测信号）Fig.10 The amplitude spectrum of vibration signal（actual measurement）

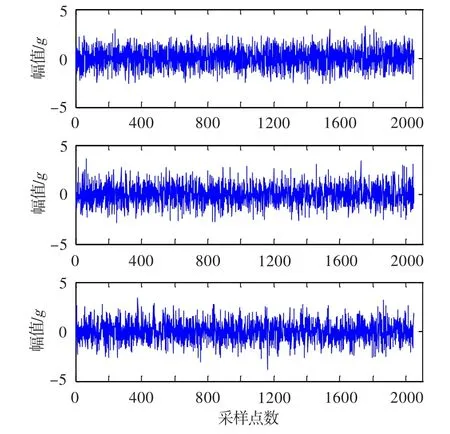
图11 直接分离后的振动信号时域波形图（实测信号）Fig.11 Vibration signal time-domain waveform after direct separation（actual measurement）

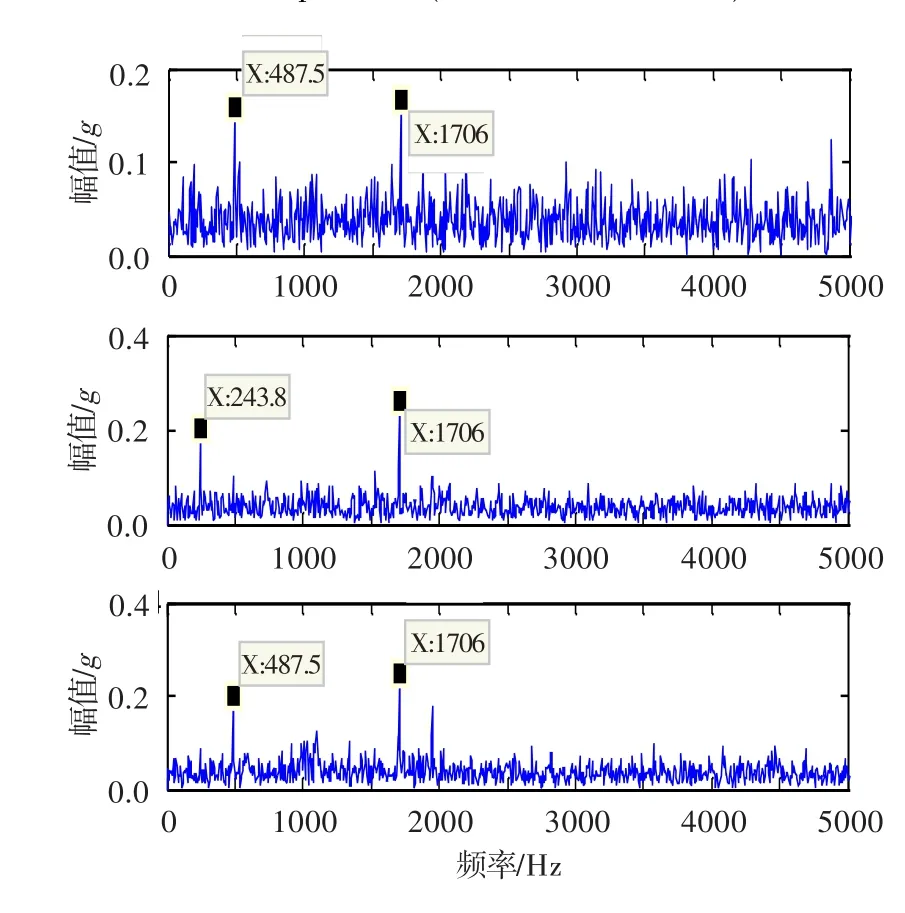
图12 直接分离后的振动信号幅值谱（实测信号）Fig.12 Vibration signal amplitude after direct separation of the spectrum（actual measurement）

采用时延自相关优化处理后分离得到的幅值谱如图13所示。可见，优化处理后噪声信号得到了较大抑制，信号分离效果良好。从上向下数第1个图存在243.8、487.5、1 219、1 706、1 950 Hz频率成分，分别对应转子的基频、2倍频、5倍频、7倍频、8倍频，表明转子系统出现非线性特征，而2倍频突出表征了裂纹故障的存在；第2个图中转子2倍频、3倍频、7倍频、8倍频突出，且2倍频幅值大于基频幅值，进一步验证了转子系统出现裂纹故障；第3个图中转子基频成分突出，表明转子系统因涡轮叶尖掉块产生了不平衡量，而出现不平衡故障特征。以上分离所得振动频率特征，与发动机实际故障吻合，这表明优化信噪比盲源分离方法，可很好地实现对航空发动机混叠振动信号的分离，有效提取故障频率成分。

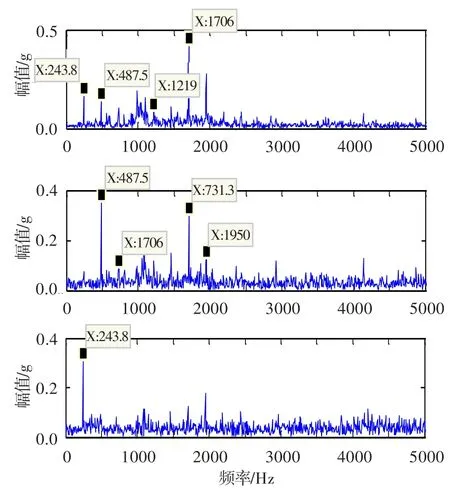
图13 优化处理后的分离信号幅值谱（实测信号）Fig.13 Optimized separated signal amplitude spectrum （actual measurement）

5　结论

通过对盲源分离原理的研究，建立时延自相关目标函数，从而优化最大信噪比盲源分离方法。利用优化信噪比的盲源分离算法，对航空发动机仿真信号和实测信号进行分析处理，结果表明：时延自相关优化处理能有效降低振动信号中的噪声，提高信噪比；优化最大信噪比分离方法，能有效分离航空发动机混叠振动信号中的不同故障特征；分离后各传感器信号频谱图基本上只显示出一种故障特征。

研究结果也表明，本文提出的方法为航空发动机振动信号的监测和故障诊断，提供了一种新的思路。但盲源分离方法在航空领域中的应用还处于探索阶段，需要对其有效性和适用性做进一步的验证研究。

参考文献：

［1］雷衍斌.航空发动机振动信号分离技术研究［D］.南京：南京航空航天大学，2010.

［2］张发启.盲信号处理及应用［M］.西安：西安电子科技大学出版社，2006.

［3］Han S H，Kim H. Extraction of rotating machine sources for fault diagnostics using independent component analysis ［C］//. Instrumentation and Measurement Technology Con⁃ference. Ottawa：2005.

［4］Nabil C，Yannick D. Self-adaptive separation of convolu⁃tively mixed signals with a recursive structure. Part 1: Sta⁃bility analysis and optimization of asymptotic behavior［J］. Signal Processing，1999，73（3）：225—254.

［5］Zhang Z L. Morphologically constrained ICA for extracting weak temporally correlated signals［J］. Neurocomputing，2008，71：1669—1679.

［6］Kokkinakis K，Nandi A K. Generalized gamma densi⁃ty-based score functions for fast and flexible ICA［J］. Sig⁃nal Processing，2007，87（5）：1156—1162.

［7］Lu W，Rajapakse J C. Approach and applications of con⁃strained ICA［J］. IEEE Trans. Neural Nets，2005，16：203—212.

［8］李舜酩，杨涛.基于峭度的转子振动信号盲分离［J］.应用力学学报，2007，24（4）：560—565.

［9］李舜酩.转子振动故障信号的盲分离［J］.航空动力学报，2005，20（5）：751—752.

［10］李舜酩，雷衍斌.转子振动信号的二阶非平稳源盲分离［J］.推进技术，2008，29（6）：747—752.

［11］李舜酩，雷衍斌.基于负熵的转子混叠振动信号盲识别［J］.中国机械工程，2009，20（4）：437—441.

［12］Cao X R，Liu R W. A general approach to blind source separation［J］. IEEE Trans. Signal Processing，1996，44：462—571.

［13］张小兵，马建仓，陈翠平，等.基于最大信噪比的盲源分离算法［J］.计算机仿真，2006，23（10）：72—75.

Application of optimized signal noise ratio algorithm in aero-engine vibration signal separation

TENG Guang-rong1，LI Shun-ming2，LIANG En-bo1，WANG Yan-feng1
（1. China Gas Turbine Establishment，Jiangyou 621700，China；2. Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China）

Abstract：In order to overcome the influence from noise on the vibration signals of aero-engine，the opti⁃mized Signal Noise Ratio（SNR）algorithm was introduced to analyze aero-engine mixed vibration signals. Based on time delay auto correction function，SNR was used to optimize the maximum signal noise ratio Blind Source Separation algorithm. The simulated mixed vibration signals were analyzed and the separated frequency spectrum was found to agree with that of the sourced signals. The faulted vibration signals from the real aero-engine tests were separated，and different fault frequencies have been found. It is proved that the optimized SNR algorithm is largely effective on mixed vibration signals separation，and it can be widely used in aero-engine tests.

Key words：aero-engine；Signal Noise Ratio（SNR）；time delay auto correlation；Blind Source

中图分类号：TN911.3；V263.3

文献标识码：A

文章编号：1672-2620（2016）02-0026-06

收稿日期：2015-07-21；修回日期：2015-12-07

基金项目：国家自然科学基金（50675099）

作者简介：滕光蓉（1976-），女，四川江油人，高级工程师，硕士，研究方向为发动机整机振动测试与分析。