极移短期预报LS建模拟合数据长度分析

王川阳，党亚民，薛树强，邱荣海

(1.山东科技大学 测绘科学与工程学院，山东 青岛　266590；2.中国测绘科学研究院，北京　100830)

极移短期预报LS建模拟合数据长度分析

王川阳1，2，党亚民2，薛树强2，邱荣海1，2

(1.山东科技大学 测绘科学与工程学院，山东 青岛266590；2.中国测绘科学研究院，北京100830)

摘要：针对高精度极移参数一般利用较长时间的空间大地测量观测进行参数估计得到，而导航定位应用需要实时极移参数的问题,采用4种最小二乘参数化方案分析数据长度对极移短期预报精度的影响。实验结果显示：不同的最小二乘拟合模型参数化方案选取的最佳数据长度不同，同一种最小二乘拟合模型参数化方案选取的最佳数据长度也会随时间缓慢且有规律的变化；最佳数据长度的选择与不同的参数化方案有关，并非越长越好，应尽量覆盖模型项的整数周期；此外极移时间序列中的信号成分具有时变性，这就需要利用最新的极移观测资料分析确定最小二乘拟合最佳数据长度，以期提高模型预报精度。

关键词：最小二乘模型；极移；短期预报；数据长度

0引言

高精度地球自转参数在空间大地测量(如全球卫星导航系统(global navigation satellite system，GNSS)、激光测月(lunar laser ranging，LLR)、航天器跟踪、深空探测等领域中具有重要地位。极移参数作为地球自转参数之一，用来描述地球瞬时自转轴在地球本体的运动。高精度极移参数一般利用较长时间的空间大地测量观测进行参数估计得到;而导航定位应用往往需要实时极移参数，用于天球坐标系和地球坐标系的相互转换[1-2]。因此，极移参数的短期预报在各种实时对地观测应用中具有重要的地位。

极移预测的常用方法有最小二乘法(least squares，LS)、最小二乘与自回归模型组合法(least squares and autoregressive，LS+AR)、最小二乘与人工神经网络组合法(least squares and artificial neural network，LS+ANN)、考虑物理激发因素的建模法。对于极移时间序列，其主要的时间尺度变化包括长趋势项和周期项(如半年项、周年项和钱德勒项)以及高频极移。高频极移很难进行参数化；因此在建立LS拟合模型时，一般对线性项和周期项进行参数化，在此基础上利用一定历史极移时间序列进行LS拟合确定其模型参数，从而建立LS预报模型[3-7]。为提高预报精度，大量研究还讨论了在LS拟合的基础上，进一步对LS拟合残差进行自回归分析并建立AR模型。

研究表明：在极移中各种周期信号的频率是随时间变化的；因此使用频率固定的周期信号进行参数化会引入一系列模型误差。这些残余模型误差往往表现为系统性误差，并导致LS拟合残差自相关。从信号处理角度，有色噪声泛指各种低频观测误差。此外在动态测量系统中，观测方程连续依赖于观测时间，一般存在大量有色噪声。利用时间序列分析和随机过程理论可以实现连续观测数据的噪声补偿和信号挖掘[8-9]。另外通过合理选取LS建模数据长度，有望补偿残余系统误差、提高LS参数估计精度，从而提高极移短期预报精度。文献[10]基于Hilbert空间理论提出连续平差模型，讨论了连续平差模型的求解方法和有色噪声的消除策略，得出有色噪声对解的影响是系统性的，通过合理的观测系统设计和采样设计，可消除有色噪声，从而实现平差解的无偏估计[10-12]。本文对比分析不同LS建模参数化方案下建模数据长度对极移短期预报精度的影响，以期确定极移短期预报LS建模所需的最佳数据长度，提高极移短期预报精度。

1LS模型数据长度选取

利用最小二乘方法建立极移短期预报模型属于一个标准的数据建模问题。通过对极移时间序列进行时频分析，理论上可以获取极移中的主要信号成分。一般情况下，研究表明，极移信号中存在模型的半年项、周年项和钱德勒项等周期信号，因此可将极移信号设为

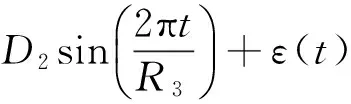
(1)式中：a0为常数项；a1为线性趋势项的系数；B1、B2为半年项的系数；C1、 C2为周年项的系数；D1、 D2为钱德勒项的系数；R1为半年项的周期182.62 d；R2为周年项的周期365.24 d；R3为钱德勒项的周期432.08 d；t为极移参数的世界协调时(coordinated universal time，UTC)时间(单位为年)。需要指出:极移时间序列中的信号并非严格的半年项、周年项等标准正弦信号所能精确模拟的，例如，周期信号频率可能是随时间变化的；因此使用上述周期项进行数据拟合时，不可避免会导致在残差时间序列中可能存在残余系统误差。进一步假设残余常数系统误差和线性系统误差可以由常数项和线性项所吸收，则残余周期性系统误差只能通过较长时间序列进行抵偿。下面以半年项、周年项及钱德勒项随机模型为例，讨论仅估计LS模型常数项和线性项时的最佳数据长度问题。由文献[10]可得线性观测模型为

(2)

式中a0和a1为待估参数，而该公式右边的周期信号作为随时间变化的误差项处理。当满足以下条件时，a0和a1的参数估计将不受半年项、周年项以及钱德勒项的影响，即

(3)

对于给定的系数B1、B2、C1、C2、D1、D2，理论上可以确定式(3)中参数t的解。满足式(3)的解top即为仅仅估计常数项和线性项时的最佳数据长度。类似的，当对半年项、周年项以及钱德勒项进行参数估计时，若在观测信号中含有未知的系统误差信号时，则类似于式(2)可建立1个参数估计不受观测系统误差影响的条件方程。

2LS建模最佳数据长度确定

考虑到式(3)中的系数B1、B2、C1、C2、D1、D2也是未知的，本文利用极移时间序列中可能的数据长度，探测建模所需的最佳数据长度。下面仅以估计常数项和线性项为例进行讨论。对于给定的等间距观测数据为

(4)

式中：t1=0为初始时刻；ti+1=ti+Δt表示地 i+1个时刻；Δt为时间序列采样间隔。对足够长的时间序列，为确定最佳数据长度top建立离散化观测方程为

Asxs=Ls+ε。

(5)

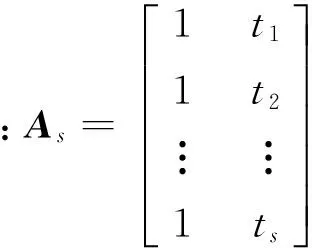
(6)

当使用数据长度为s的时间序列进行参数估计时，为了评价预报精度，可采用平均绝对误差(meanabsoluteerror，MAE)作为精度评定标准，其计算公式为

(7)

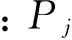
(8)

即当sMAE达到最小时的时间序列长度ts作为式(3)的近似解。

类似地可以讨论增加估计半年项、周年项以及钱德勒项情形下的最佳数据长度问题，相关讨论略。

3实验与结果分析

3.1方案设计

利用国际GNSS服务组织(international GNSS

service，IGS)公布的igs95p02.erp序列，选取2010年第182 d到2015年第181 d的数据序列，包含极移分量X和Y、日长变化LOD、地球自转速率UT1-UTC等，时间间隔为1 d。将数据分为4组，见表1。

表1中数据长度均为500 d，分别采用下述方案1～4建立极移参数X、Y预报的LS预报模型。

方案1：仅估计常数项、线性项；

方案2：仅估计常数项、线性项、半年项；

方案3：仅估计常数项、线性项、半年项、周年项；

方案4：全部估计常数项、线性项、半年项、周年项、钱德勒项。

限于篇幅，仅以第1组数据来具体说明。方案1采用第1组数据2010年第182 d开始，截取10 d、11 d、…、500 d分别建立仅仅参数化常数项和线性项的LS预报模型，即式(5)中s=10，11，…，500。评价其模型预报精度时，向后预报3 d并将IGS公布的极移产品作为真值，采用式(7)计算sMAE(k=3)。

3.2结果与分析

试验表明：仅对部分周期信号进行参数化时，明显存在最佳数据长度的选取问题；而且使全部考虑对常数项、线性项、半年项、周年项和钱德勒项进行参数化，也不是使用的数据长度越长越好。导致这种现象的原因可能是在极移信号中存在未参数化的残余系统误差影响，这也是本文研究的基础和意义所在。下面重点分析X分量的试验结果,如图1～4所示。

图1　第1组数据的4种方案测试结果图

图2　第2组数据的4种方案测试结果图

图3　第3组数据的4种方案测试结果图

图4　第4组数据的4种方案测试结果图

试验表明：利用本文提出的方法可以确定极移短期预报LS建模的最佳数据长度的多个极值点；比较这些极值点，可以确定最小点，其最小点可作为建立最优LS预报模型的参考依据。随着拟合数据长度的增加，方案1和方案2预报精度逐渐降低，随后又出现精度较高的极小值点，这与未参数化的周期项信号在极小值处得到抵偿有关。方案3和方案4出现很多极小值点，这是因为考虑了低频极移信号之后残余的高频极移信号，且难以对高频极移信号进行参数化的缘故。

由于极移时间序列中的信号成分往往具有时变性，随着极移时间序列向后推移，LS拟合最佳数据长度也会随时间缓慢且有规律地变化，例如方案1从第1组到第4组数据，第1组数据对应的第一个极值点为第323 d，第2组数据对应的第一个极值点为第243 d，第3组数据对应的第1个极值点为第237 d，第4组数据对应的第一个极值点为第148 d。方案2也存在相同的规律，但其第1个极小点相对与方案1滞后大约10～40 d不等，而其第2个极小值点与方案1基本重合。这就需要利用最新的极移观测资料分析确定LS拟合最佳数据长度，以期提高模型预报精度。

本文4种方案的预报结果都采用平均绝对误差作为评定精度的标准，并以此来确定最佳数据长度。各组数据4种方案的预报精度和最佳数据长度的统计结果见表2，表2数值单位mas为毫角秒。

表2　各组数据4种方案的预报精度统计

4结束语

本文基于最小二乘模型对极移短期预报中的最佳数据长度进行试验分析，通过比较4种不同方案得出以下结论：最佳数据长度的选取与LS拟合模型不同的参数化方案有关，最佳数据长度并非越长越好，应尽量覆盖LS拟合模型项的整数周期；由于极移时间序列的信号成分复杂，对建模数据长度进行优化选取可以提高LS拟合精度；极移时间序列中的信号成分往往具有时变性，随着极移时间序列的向后推移，LS拟合模型参数化方案选取的最佳数据长度也会随时间缓慢且有规律的变化，这就需要利用最新的极移观测资料分析确定最小二乘拟合最佳数据长度，以期提高模型预报精度。

参考文献

[1]孙张振，徐天河，范朋飞.基于LS+AR模型的极移预报及其周期项影响分析[J].测绘通报，2012(增刊1)：16-19.

[2]魏二虎，杨亚利，金双根，等.利用LS_AR模型对极移参数的中长期预报[J].测绘地理信息，2014，39(4)：5-9.

[3]王小辉.改进极移预报的研究[D].长沙：中南大学，2013：22-30.

[4]张昊.地球定向参数极移的预报理论与方法研究[D].长沙：中南大学，2012：12-19.

[5]严凤，姚宜斌.地球自转参数短期预报方法及其实现[J].大地测量与地球动力学，2012，32(4)：71-75.

[6]许雪晴.地球定向参数高精度预报方法研究[D].上海：中国科学院研究生院，2012：28-44.

[7]李军，赵德军，陈永祥.利用LS+AR模型和激发函数预报地球自转参数[J].大地测量与地球动力学，2015，35(3)：457-459.

[8]周江文.系统误差的数学处理[J].测绘工程，1999，8(2)：1-4.

[9]杨元喜，崔先强.动态定位有色噪声影响函数——以一阶AR模型为例[J].测绘学报，2003，32(1)：6-10.

[10]薛树强，杨元喜.连续观测系统平差模型与有色噪声补偿[J].测绘学报，2014，43(4)：360-365，371.

[11]赵建远，李醒飞，田凌子.有色噪声背景下的正交子空间辨识[J].控制理论与应用，2015(1)：43-49.

[12]薛树强，党亚民，陈武.最小二乘估值均方差计算的矩阵体积法[J].武汉大学学报·信息科学版，2009，34(9)：1106-1109.

Data length analysis of LS fitting for short-term forecast of polar motion

WANG Chuanyang1，2，DANG Yamin2，XUE Shuqiang2，QIU Ronghai1，2

(1.Geomatics College，Shandong University of Science and Technology，Shandong Qingdao 266590，China；2.Chinese Academy of Surveying and Mapping，Beijing 100830，China)

Abstract：Aiming at the problem that high-precision pole motion parameters are generally obtained by parameter estimation through long-term spatial geodetic observations，while navigation and position require real-time pole motion parameters，this paper analyzed the influence of the data length on forecast accuracy by using four least squares parameterization schemes.The results showed that different least squares fitting parameterization schemes corresponded to different optimal data length;the optimal data length of the same least squares fitting parameterization scheme varied over time slowly and regularly.It indicated that the optimal data length would be related to different parameterization schemes and not as long as possible,but should cover the cycle of model items.In addition，since the signal components of pole motion series are often time-varying，it should use the latest polar motion observations to analyze and determine the least squares fitting data length in order to improve the forecast accuracy.

Keywords：least squares；polar motion；short-term；data length

收稿日期：2015-12-18

基金项目：国家自然科学基金项目(41020144004;41104018);国家科技支撑计划项目(2012BAB16B01);国家863计划项目(2009AA121405，2013AA122501);北斗全球连续监测评估项目(GFZX0301040309);福建省海岛与海岸带管理技术研究实验室开放基金项目;北斗动态参考框架维持关键技术及其应用项目(7771416)。

第一作者简介：王川阳(1991—)，男，河南许昌人，硕士研究生，研究方向为地球自转参数预报。

中图分类号：P228

文献标志码：A

文章编号：2095-4999(2016)02-0062-05

引文格式：王川阳，党亚民，薛树强，等.极移短期预报LS建模拟合数据长度分析[J].导航定位学报，2016，4(2)：62-66.(WANG Chuanyang，DANG Yamin，XUE Shuqiang，et al.Data length analysis of LS fitting for short-term forecast of polar motion[J].Journal of Navigation and Positioning，2016，4(2)：62-66.)DOI：10.16547/j.cnki.10-1096.20160213.