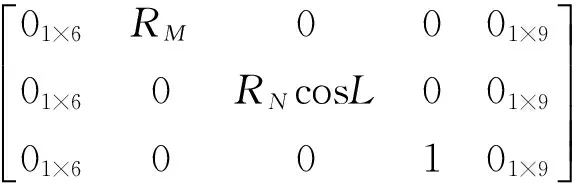单星跟踪的组合天文定位算法

周　磊，张　锐，樊建文

(中国电子科技集团公司 第二十研究所，西安　710068)

单星跟踪的组合天文定位算法

周磊，张锐，樊建文

(中国电子科技集团公司 第二十研究所，西安710068)

摘要：针对机载平台下小视场天文导航定位高度差算法的应用缺陷，提出了一种基于单星跟踪的组合天文定位算法，并以此解决了当双星的方位张角接近180°时的天文定位问题：首先分析了机载平台下天文/惯性组合导航系统中的小视场天文定位的特点；然后阐述了组合天文定位算法的具体过程；最后建立了机载天文观测仿真模型。仿真结果表明该算法性能优良，能够有效减小天文定位算法对选星的依赖，拓宽天文定位算法的应用范围。

关键词：机载CNS/INS组合导航；星体跟踪器；单星定位；高度差法

0引言

天文导航通过天体敏感设备观测天体，确定载体位置等导航参数，由天体的不可摧毁性和可预知性，使天文导航系统相对其他导航系统具有如下的特点：相比于惯性导航系统，天文导航具有误差不随时间增长的特点；相比于卫星导航系统，天文导航具有独立、无源、不受人为因素限制和干扰等特点。因此，天文导航是现代高科技战争中不可或缺的一种重要的导航方式。但是，天文导航受到天文观测因素的影响，数据输出不连续；因而常作为一种重要的导航辅助手段，与主导航系统(一般为惯性导航系统)构成组合导航系统[1-2]。

根据天文导航系统测星设备的视场不同，天文导航系统可分为小视场天文导航系统(如六分仪、星体跟踪器)、大视场天文导航系统(如星敏感器[3]，视场为8°×8°～50°×50°)。相比于大视场天文导航系统，小视场天文导航系统适合用于背景光噪声较大的大气环境中。而机载平台的天文导航定位系统虽然大多运行于大气运动较为平稳的平流层内，但大气光学效应依然给天文观测带来了较大的影响。因此，基于星体跟踪器的天文导航系统成为机载天文导航的首选。

美国很早就开展了基于机载小视场星体跟踪器模式的相关研究，研制了多款天文/惯性组合导航系统，并成功应用于多个机载平台，如NAS-26/27、LN-20LN-120G等[4-6]。国内关于机载平台的天文导航，多着墨于未来的星敏感器大视场观星模式，并处于理论和实验研究阶段[7]；而对于基于小视场的机载天文导航则研究较少，也没有成熟的产品应用于航空平台。

基于此，本文针对机载平台下的小视场天文导航定位算法展开了研究：分析了机载平台下天文/惯性组合导航系统中的小视场天文定位的特点，指出了当前的天文定位算法在机载平台下应用的缺陷，并以此提出了一种组合天文定位算法，解决了当双星的方位张角接近180°时的天文定位问题。

1天文定位算法原理

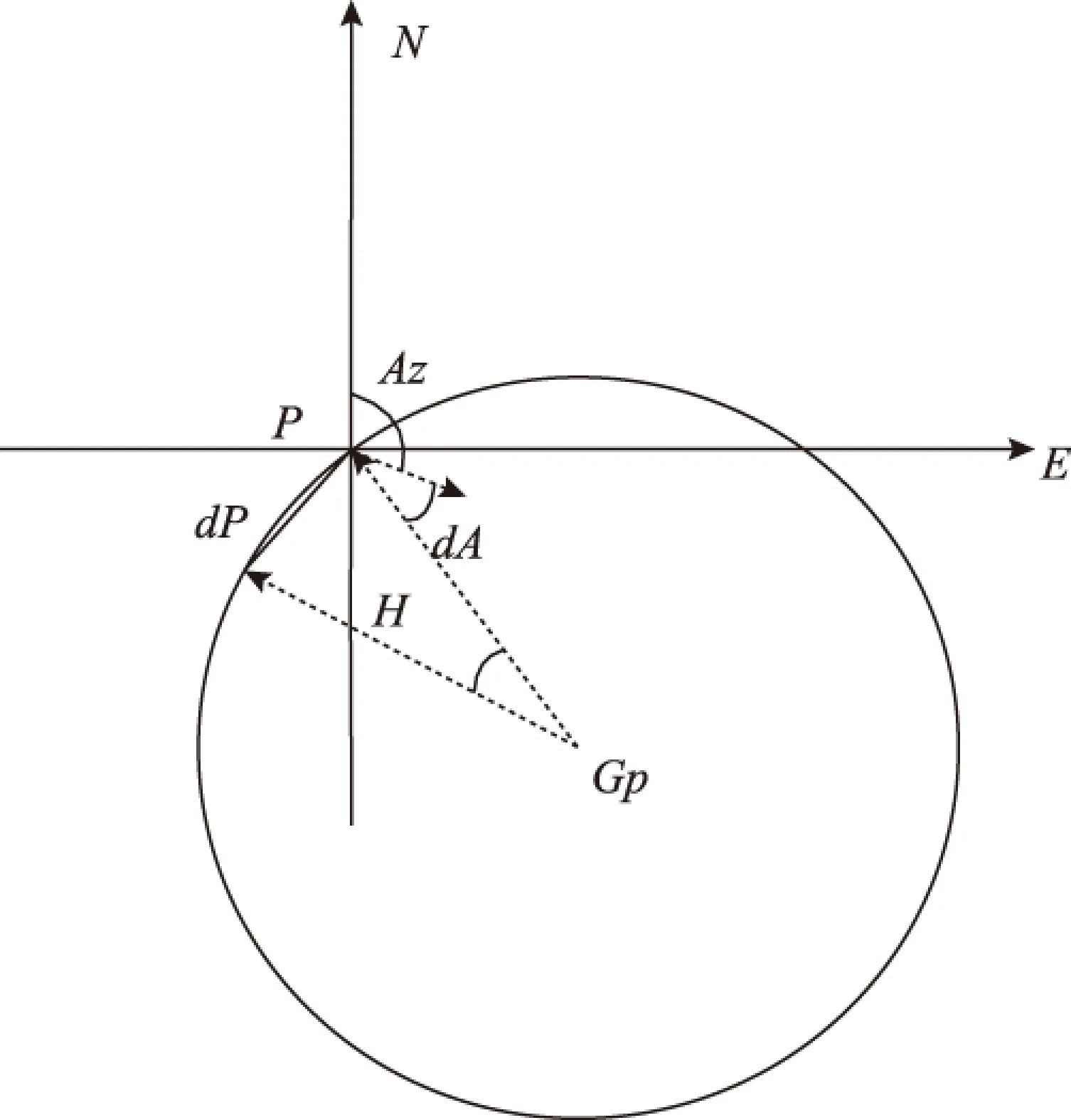
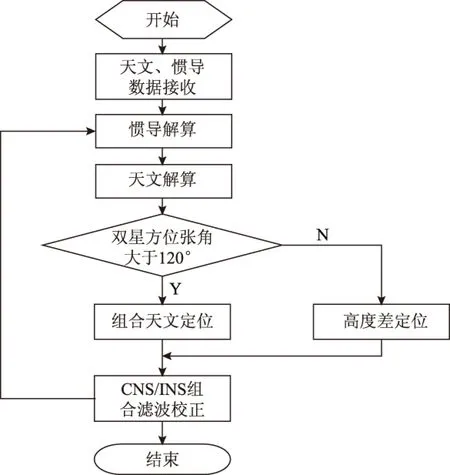
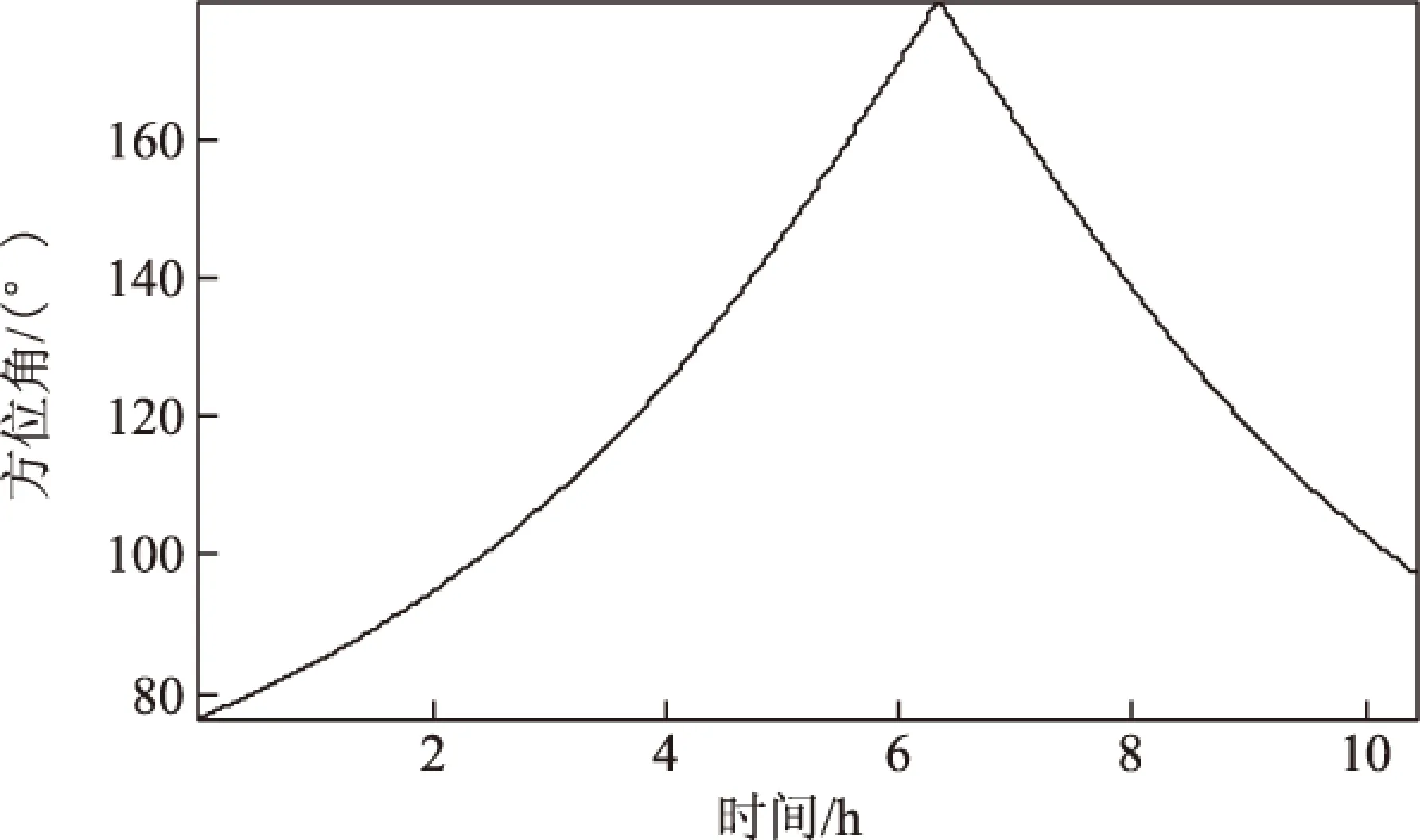
基于天文/惯性的组合导航系统中，由于惯导系统的方位角误差易随时间积累，因此误差较大。高度差法的算法中间过程中，虽然也引入了方位角信息，但最终的评判结果是以观测的高度角为基准；因此避免了方位角误差对天文定位精度的影响，在多星观测天文定位中性能优良，一直沿用至今。但是，由于机载平台的高速性和环境复杂性导致平台稳定性较差，且单星跟踪器的视场较小，不能短时间内连续切换观测多颗导航星；考虑到后续的滤波周期问题，一般以连续观测两到三颗星为宜。此时，高度差法对恒星的分布有一定的要求，任意2颗星的观测方位张角Az最好处于(60°

1.1组合单星定位算法及误差分析

文献[7]说明在精确测量高度角和方位角的情况下，在同一颗导航星下，任意一组观测的高度角和方位角对应唯一一个观测位置。因此，可以利用单颗导航星实现天文定位，其定位计算方法如下：

由星体跟踪器观测天体，获得观测高度角H0， 和方位角A， 由天文历获得观测天体的投影点位置。假设观测点的初始经纬度位置已知，则通过导航三角求解，高度角Hc表示为

Hc=arcsin(sinLat0·sinDec+cosLat0·

cosDec·costAP)。

(1)

式中：Lat0为观测点初值位置纬度值；天体赤纬Dec和天体格林时角GHA由导航星历计算获得；tAP为子午线角。tAP由式(2)计算可得

(2)

式中Lon0为观测点初值位置经度值。由Hc、 Lat0、 Dec计算天体在P处的方位角为

(3)

联立式(1)～式(3)可知:此时未知数只有观测点位置初值P(Lon0，Lat0)； 因此可以计算出观测点位置，实现单星定位。假设测量高度角误差较小可以忽略，并设方位角误差为dA， 此时单星观测的定位误差dP如图1所示。

图1　单星定位误差随方位角误差增大而增大

图1中，方位角误差dA较小，可以看做小量，则单星定位误差与方位角误差的关系为

dP=H·sin(dA)。

(4)

由式(4)可知：此时天文定位误差与方位角观测误差的正弦值和高度角成正比，说明采用这种定位方法，高度角对定位误差有放大作用。因此，除非当方位角误差得到了很好的校正且只有一颗导航星的信息时可以考虑，否则一般不建议采用该方法用于天文定位。但是当采用双星定位时，分别对两颗星进行单星定位解算，并取其均值作为天文定位结果，即有

(5)

式中:Lon1、Lon2为单星分别定位的经度估计值；Lat1、Lat2为单星分别定位的纬度值。此时的定位误差如图2所示。

图2　定位误差随双星方位张角增大而减小

从图2可以看出：在天文/惯性的组合导航系统中，方位角误差主要来自于惯导的航向角测量误差；根据惯导的性质可知，当同时观测2颗导航星或短时间内连续观测2颗导航星时，其方位角误差几乎保持不变，即有dA=dA1=dA2， 则观测2颗恒星的方位张角Az=A2-A1为准确测量值。综上所述，假设天文观测高度角H1≤H2， 解三角形dP1_P_dP2可得天文定位误差dP为

H1·sin(dA)·cos(Az/2)≤dP≤

H2·sin(dA)·cos(Az/2)。

(6)

从式(6)可以看出：天文定位误差与Az/2的余弦值成正比；因此当观测双星的方位张角接近180°时，cos(Az/2)趋近于零，即此时的天文定位误差也很小。而此时，由于高度角测量存在误差，双星测量的等高圆可能不相交，即高度差法和多圆交汇法的估计误差极大或不可用。

根据上面的分析，本文提出组合天文定位算法：以双星观测的方位张角为基准，当方位张角接近180°时，采用上述的组合单星定位方法；而在其他区域依然采用传统的高度差或多圆交汇法。

1.2CNS/INS组合导航滤波

通过天文定位(celestial navigation system,CNS)得到载体的位置信息后，结合惯性导航系统(cinertial navigation system,INS)得，组成CNS/INS组合导航系统；采用线性卡尔曼滤波器对系统的误差进行滤波，实时校正惯性导航系统的位置误差[8-10]。其组合导航系统框图如图3所示。

图3　CNS/INS组合导航系统

图3中:以惯导和天文定位的位置误差作为观测量；卡尔曼滤波的系统状态方程为惯导INS 的误差方程，导航坐标系选为东北天地理坐标系。根据INS系统的误差源性质，可得误差方程为

(7)

系统状态变量为

X=(φe，φn，φu，δve，δvn，δvu，δL，δλ，δh，

εbx，εby，εbz，εrx，εry，εrz，x，y，z)。

(8)

式(8)中:φe，φn，φu为捷联惯导数学平台误差角；δve，δvn，δvu为速度误差；δL，δλ，δh，为纬度、经度和高度误差；εbx，εby，εbz，εrx，εry，εrz分别为陀螺常值漂移误差和一阶马尔可夫漂移误差；x、y、z为加速度计零偏。此时系统的量测方程为

Z(t)=H(t)X(t)+V(t)。

(9)

2仿真分析

结合上述天文定位方法，对CNS/INS组合导航系统进行仿真验证。其组合天文定位的流程如图4所示。

设组合导航系统中，惯导的定位精度为CEP=1.5 nmile/h，并实时为天文观测提供姿态信息；星体跟踪器能够保持稳定观星，导航星观测误差为30″(1σ)， 包含参考水平基准和星体跟踪器观测误差。为更好地验证组合定位算法的优势，设计以下仿真环境：天文观测采用定点观测，观测点位置为(34.242 7°N，108.544 5°W)，并在观测点纬线两边各选一颗导航星，进行长时间(10 h)的跟踪观测，导航星的初始格林时角为GHA=(160°，180°)， 赤纬为Dec=(0°，70°)； 并设星体跟踪器每隔20 s对2颗星观测一次，因此，组合导航的卡尔曼滤波周期也设为20 s。

在上述实验条件下，仿真结果如图5所示。

图4　组合天文定位算法流程图

图5　惯导输出的位置误差

图6　双星观测的方位张角变化

图5为惯导在没有校正前输出的位置误差。可以看出：在10 h内定位误差随时间不断增大，达到1.5 nmile/h。图6为在10 h内，对上述2颗导航卫星连续观测时，其观测的相对方位张角变化情况。可以看出：其方位张角不断增大，在6.2 h附近达到最大(接近180°)，然后持续下降。由于高度差法的最佳方位张角范围为(60°～120°)，图6中4～9 h内是不符合高度差法天文定位的要求的；因此，本文对高度差法定位和组合天文定位结果进行了对比分析，结果如图7～图10所示。

2.1高度差法定位及滤波

图7为10 h内高度差法的天文定位结果。可以看出：在前4 h内，定位误差较小；在4～9 h内定位误差不断增大，并在6.2 h处，其定位误差达到峰值(>100 nmile)。图8为对应高度差法的组合导航滤波结果，可以看出：在符合高度差法的定位要求的时间段内，组合滤波结果较好，组合定位误差约CEP=0.2 nmile；在不符合要求的时间段内，组合滤波的结果很不理想，组合滤波定位误差峰值达到40 nmile；在10 h内，总体的组合滤波误差CEP=2.83 nmlie。

图7　高度差法定位误差

图8　基于高度差法定位的组合导航滤波结果

2.2组合天文定位及滤波

图9为组合天文定位的定位误差。可以看出：在整个观测时间段内，天文定位的估计误差约为0.6 nmile。

图9　组合天文定位的解算误差

图10为基于组合天文定位的组合导航滤波结果。可以看出：在整个观测时间段内，组合导航滤波的定位误差约为CEP=0.15 nmile。对比可以发现，组合天文定位可以有效解决双星定位中大方位张角的天文定位估计问题；在保证定位精度的基础上，降低了天文定位估计对选星条件的依赖；从而提高了组合导航系统的稳定性和可靠性。

图10　基于组合天文定位的组合导航滤波结果

3结束语

本文从小视场天文定位算法的定位误差分析出发，分析了传统高度差法和多圆交汇法在机载平台下的天文定位的局限性，提出了一种组合天文定位算法。在此基础上，分析了该算法的定位理论误差，并建立仿真实验系统，实现了基于该算法的组合导航滤波。理论和仿真验证结果表明，该算法性能优良，解决了当双星观测方位张角接近180°时的天文定位问题，减小了天文观测对选星算法的依赖。下一步工作，将搭建天文/惯性组合导航实验系统，深入开展实验研究，为该方法的工程化奠定基础。

参考文献

[1]屈蔷.机载捷联惯性/天文组合导航系统关键技术研究[D].南京：南京航空航天大学，2011：10-28.

[2]VAN ALLEN J A.Basic principles of celestial navigation[EB/OL].(2007-09-07)[2015-08-12].http：//astro.physics.uiowa.edu/～rlm/mathcad/AJP001418.pdf.

[3]孙才红.轻小型星敏感器研制方法与研制技术[D].北京：中国科学院，2002：44-78.

[4]NORTHNOP G.LN-120G stellar-inertial navigation system[EB/OL].[2015-08-12].http：//www.northropgrumman.com/Capabilities/LN120GStellarInertialNavigationSystem/Pages/default.aspx.

[5]许国祯.B-2隐身轰炸机作战性能剖析-精确导航与制导武器系统[J].惯性世界，1999(2)：19-22.

[6]ATKINSON D，AGNEW J，MILLER M.The B-2 navigation system[C]// The Institute of Electrical and Electronic Engineers(IEEE).Proceedings of the IEEE 1993 National Aerospace and Electronics Conference(NAECON 1993).Dayton，OH：IEEE，1993：15-34.

[7]房建成，宁晓琳.天文导航原理及应用[M].北京：北京航空航天大学出版社，2006：69-90.

[8]秦永元，张洪钺，汪淑华.卡尔曼滤波和组合导航系统[M].西安：西北工业大学出社，1998：33-75.

[9]周磊，樊建文，张锐.基于机载星体跟踪器的天文定位算法研究[EB/OL].中国卫星导航系统管理办公室学术交流中心.第五届中国卫星导航学术年会论文集.北京：中国卫星导航系统管理办公室，2014：1-5.

[10]杨建强，侯建军.自适应惯性/天文器件级组合导航算法研究[J].光学与光电技术，2013，11(5)：44-51.

A combined celestial positioning algorithm based on single star tracking

ZHOU Lei，ZHANG Rui，FAN Jianwen

(The 20th Research Institute of China Electronics Technology Group Corporation，Xi’an 710068，China)

Abstract：In view of the celestial positioning problem of multiple circle intersection iterative algorithm and height difference method on airborne platform，a combined combination celestial positioning algorithm with single star was proposed，with which the celestial positioning problem when the observation angle of two stars close to 180 degree was overcomed.Then the characteristic of traditional celestial positioning method was discussed and the theory of this algorithm was given in this work.Finally，an airborne celestial observation simulation model was established，and the simulation results demonstrated that the performance of this method would be excellent.What’s more，the reliance on selection and combination of the stars could be reduced and the application of celestial positioning could be extended.

Keywords：airborne CNS/INS integrated navigation；star tracker；single star positioning；height difference method

收稿日期：2015-09-16

第一作者简介：周磊(1984—)，男(土家族)，湖北五峰人，博士，工程师，研究方向为天文导航及综合导航。

中图分类号：P228

文献标志码：A

文章编号：2095-4999(2016)02-0042-05

引文格式：周磊，张锐，樊建文.单星跟踪的组合天文定位算法[J].导航定位学报，2016，4(2)：42-46.(ZHOU Lei，ZHANG Rui，FAN Jianwen.A combined celestial positioning algorithm based on single star tracking[J].Journal of Navigation and Positioning，2016，4(2)：42-46.)DOI：10.16547/j.cnki.10-1096.20160209.