基于P空间的上海、北京、广州3个城市轨道交通网络拓扑结构比较
周溪召, 智路平, 马洪伟
(1. 上海海事大学 经济管理学院, 上海 201306; 2. 上海理工大学 管理学院,上海 200093; 3. 上海电机学院 商学院, 上海 201306)
基于P空间的上海、北京、广州3个城市轨道交通网络拓扑结构比较
周溪召1,2,智路平1,2,马洪伟3
(1. 上海海事大学 经济管理学院, 上海 201306; 2. 上海理工大学 管理学院,上海 200093; 3. 上海电机学院 商学院, 上海 201306)
摘要针对上海、北京和广州3个城市地铁实际网络及运营关系,分别构建了P空间拓扑结构模型。基于复杂网络理论,应用特征统计指标对上海、北京和广州3个城市轨道交通网络拓扑结构特征进行了分析。首先比较在P空间上网络各特征值的差异;其次,分析比较3个城市轨道交通网络的度及度分布、平均最短路径及分布、网络聚类系数等特征指标;最后还对P空间下的聚类系数与度的关系进行了分析,发现上海、北京和广州3个城市各有特点,并无规律。从3个城市的聚类系数及度分布表明: 它们都有高的聚类系数和较小的度值,说明在P空间下,大城市轨道交通网络具有复杂网络特征,都是小世界网络,这对进一步研究地铁线网的结构特性具有启示作用。
关键词城市轨道交通网络; 拓扑结构; P空间
轨道交通因其大运量、高速度、安全可靠、准点舒适等特点,让各国普遍认识到: 解决大城市交通问题的根本出路在于优先发展以轨道交通为骨干的城市公共交通系统。我国已经进入了轨道交通网络高速发展的时期,2015年总运营里程已达3000km※。随着轨道交通建设的不断发展,北京、上海、广州等大城市的轨道交通系统已经进入了网络化时代,轨道交通线网规划的重点也由原来的单线转移到了网络结构。因此,对我国轨道交通网络结构的研究将有助于我们了解城市轨道交通网络的发展,从而更好地管理和引导交通网络的演化。
18世纪著名数学家欧拉解决了“Konigsberg”七桥问题,首次引入了交通网络概念。从此之后,学者们试图进一步了解交通网络及时空变化,20世纪90年代,随着网络科学的出现,激发了相关领域学者们对复杂网络的研究兴趣[1]。研究主要集中在根据网络的拓扑结构特征来划分网络的类型: Barabasi等[2]认为如果节点的度分布服从指数分布,则认为该网络为随机网络;如果节点的度分布服从于幂律分布,认为该网络属于无标度网络;如果随机网络具有较小的特征路径长度和较大的聚类系数,认为该网络为小世界网络[1]。但是对交通网络的复杂性研究相对较少,高自友等[3-4]研究了交通网络区别于其他网络的复杂性,针对公交网络研究了其无标度特性及度分布指数;Sienkiewiez[5]研究了22个城市公交系统的统计特征;Chen、汪涛等[6-8]研究了城市公交网络的拓扑结构及其演化模型,发现经过站点的公交网络服从幂律分布,并提出了公交网络的演化生成机制;Sen、Seaton等[9-10]发现并研究了铁路网
络的小世界特性;Jiang[11]研究了城市道路网络的演化规律;Rui等[12]提出了一种自组织的城市道路网络模型,并研究了这种网络的进化及成长机制。综上,相对于城市交通网络、铁路网络的研究,目前对城市轨道交通网络的研究相关较少[13-14]。
本文选取中国轨道交通网络发展最好的3个城市来进行分析比较,统计这些城市轨道交通网络在P空间下的各种拓扑特征值,从而为今后轨道交通网络演化提供依据。
1北京、上海和广州轨道交通网络描述
本文选取目前轨道交通网络化较为成熟的上海、北京、广州3个城市的轨道交通网络进行比较分析。上海、北京、广州3个城市的轨道交通网络统计信息如表1所示[15]。

表1 北京、上海和广州3城市轨道交通网络的统计情况
表示城市轨道交通网络的方法有多种,P空间是其中一个方法。为了研究需要,作如下定义:
定义1P空间(Space P)[16-17]。将交通站点视为节点,若两个站点有直达的轨道线路,那么它们就有连边;若没有,则站点不相连。
定义2度[18]。交通网络中与某节点相连接的边的数目为该节点的度。
定义3度分布[18]。交通网络中节点的度分布P(k)可以用来表示度值为k的节点占总节点的比例数。
定义4累计度分布[18]。定义3中度分布表示交通网络中所有节点度的概率分布函数P(k′),为了减少统计误差和提高拟合精度,一般采用的表达方式是累积概率分布函数

(1)
式中,P(k≥k′)是指度k≥k′的概率。
定义5最短路径[18]。在P空间中从源点到终点所含边的数目最少的路径称为最短路径。
定义6节点聚类系数[18]。在网络中节点i有ki条边把它与其它节点相连,则这ki个邻居之间最多有ki(ki-1)/2条边相连,若事实上这ki个节点之间有Ei条边相连,则定义i的聚类系数为
(2)
定义7网络聚类系数[18]。整个网络的聚类系数C就是网络中所有节点(总数N)的聚类系数的平均值
(3)
式中,ki为与节点i相连接的边数;Ei为ki个节
点之间边的个数;Ci为节点i的聚类系数;N为网络中所有节点个数。
2度与度分布分析
据定义2和3,可求出上海、北京、广州3个城市的度及度分布情况,如表2和图1所示。
从图1中可以看出,上海轨道交通网络的度分布较集中,节点度在20~30的比例较高,而北京轨道交通网络的度分布跨度(3~70)没有上海跨度(5~104)广,分布相对平均。广州轨道交通网络度分布跨度(8~46)相对较小,这是因为广州轨道交通网络整体规模较小,线路所拥有的站(节)点数相对较少(上海最长线路为31个节点,平均24.67个节点,北京最长线路为42个节点,平均为17.4个节点,广州最长线路为24个节点,平均16.2个节点),而且广州轨道交通网络的两线和三线相交节点相对于上海和北京少很多,这使广州市轨道交通网络的度分布跨度较小,且整体度值较低,这与其规模相符合,广州市轨道交通线网现在所具有的度分布特点是与上海和北京轨道交通线网的前期是类同的。
据定义3,可求出北京、上海、广州3个城市的累积度分布,如图2所示。

表2 上海、北京和广州3个城市轨道交通网络P空间下度对比
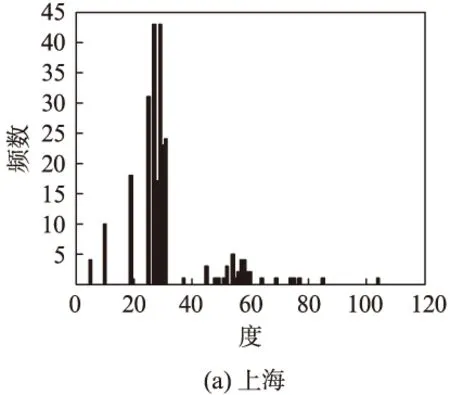

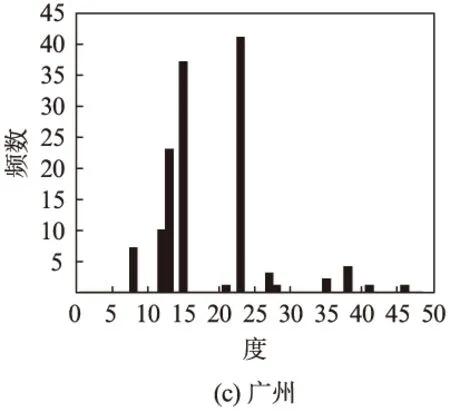
图1 3个城市P空间下的度分布情况



图2 3个城市累积度分布对比Fig.2 Comparison of cumulative distributions of the 3 cities
从图2不难看出,3个城市轨道交通网络的度分布接近幂率分布。
3最短路径
据定义5,可求出上海、北京和广州3城市轨道交通网络的最短路径,如表3所示。由表3可见,上海轨道交通网络的平均最短路径长为2.15,即从上海轨道线网中的任一站点,平均只要换乘1.15次就能到达其他任一站点,广州轨道交通网络的平均最短路径长为2.37,北京轨道交通网络的平均最短路径长为2.56,在3个城市中是最大的。这说明上海市轨道交通线网具有较好的换乘

表3 上海、北京和广州3城市轨道交通网络最短路径分析
可达性,北京市轨道交通网络最短路径长较大是因为北京市后期开通的线路(如机场线、亦庄线、房山线、昌平线、15号线和8通线)均在郊区,它们都只与前期网络的一个站点连接,这导致它们到其他线路至少要换乘2次以上,网络的最大最短路径长为5,就是其换乘效率较低的一个表征。
4聚类系数分析
据定义6和定义7,可求出北京、上海、广州3个城市轨道交通网络的聚类系数,如表4和图3所示。
从表4和图3可以看出,在P空间下,每个城市都有超过80%以上的节点的聚类系数为1。上海的最小聚类系数最小为0.2619,是世纪大道站,这是因为在该站点有4条线路通过。3个城市的平均聚类系数都超过了0.9,说明聚类系数高是在P空间下轨道交通线网的特点。广州轨道线网的平均聚类系数最高为0.9453,这是因为广州轨道交通线网的换乘节点占总站点数的比例相对较少,从而聚类系数为1的站点比例较高,提高了整个线网的平均聚类系数。从3个城市的聚类系数及前述度分布可知,它们都有高的聚类系数和较小的度值,说明在P空间下,大城市轨道交通网络都是小世界网络。

表4 3个城市轨道交通网络聚类系数分析



图3 3个城市的聚类系数分布情况Fig.3 Distribution of cluster coefficient in the 3 cities
5聚类系数与度的关系
对上海轨道交通的复杂网络特征进行统计后得出: 节点度k<22时,聚类系数随节点度的增加没有变化,保持常数1,如图4所示;但当k≥22时,通过拟合,可以用一个幂函数k-β来描述P空间中聚类系数C(k)随节点度的变化关系,其中,β=0.82,聚类系数的这种标度行为表明该网络具有层次结构和模块性质,这与文献[16]中的观点一致。为了验证这一结论,对北京、上海和广州3个城市的聚类系数与度值的关系进行了分析,如图5所示,发现北京和广州两个城市的结果则没有明显的变化规律。因此本文认为,在目前中国城市轨道交通线网的规模下,聚类系数与度值的关系并不十分明显,这与整个线网的发展成熟度相关。同时,从聚类系数的计算方法可知,一个节点通过的线路越多,其聚类系数就越小,当节点只有一条线路通过时,该节点的聚类系数为1。而对于有2条及以上线路通过的节点,其聚类系数就跟通过该点的各条线路所拥有的节点数有关,且各条线的节点越多,该节点的度值越大,聚类系数也越小,反之也然。但由于我国轨道交通网络中线路的节点分布范围较广,既有由几个节点组成的线路,也有由几十个节点组成的线路,如北京和广州轨道交通网。这从某种程度上解释了为什么度与聚类系数并不一定存在统一的变化规律。

图4 上海市轨道线网P空间中聚类
Fig.4Relationship of clustering coefficient with the node degree in space P of the mass transit network of Shanghai mass transit network
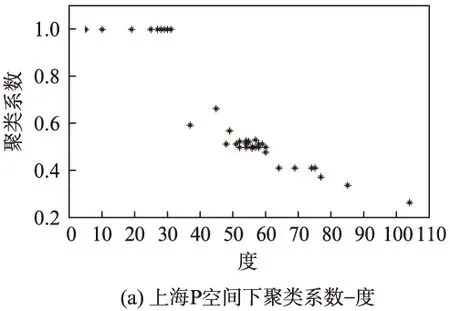

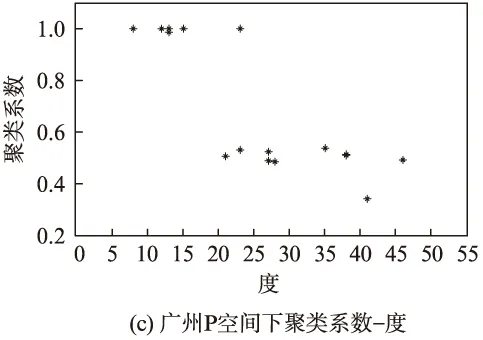
图5 3个主要城市轨道交通网络P空间下聚类系数随节点度的变化关系
Fig.5Relationship of clustering coefficient with node degree in space P of the 3 major urban mass transit networks
6结论
通过对上海、北京和广州3个城市的轨道交通网络拓扑结构的分析,获得了在P空间视角下轨道交通网络所具有的性质,可以看到,在P空间下,网络整体的度值很高,且分布区域也很广,而网络的平均最短路径很小,它反映的是从一个站点到任意一个站点平均需要换乘的次数,网络的聚类系数很大,都超过了0.9,北京、上海和广州3个城市都有超过80%以上的节点的聚类系数为1。最后还对P空间下的聚类系数与度的变化关系进行了分析,发现上海、北京和广州3个城市各有特点,并无统一规律。从3个城市的聚类系数及度分布表明: 它们都有高的聚类系数和较小的度值,说明在P空间下,大城市轨道交通网络具有复杂网络特征,都是小世界网络,得到的结果是今后网络演化规则制定过程的重要依据。以上结果表明,大城市地铁网络属于复杂网络,其不同统计指标的分布规律可帮助我们揭示其内在形成机理,为研究大城市轨道交通网络演化奠定了基础。
参考文献
[1]WATTS D J,SSROGATZ S H.Collective dynamics of ‘small-world’ networks[J].Nature,1998,393(6684): 440-442.DOI: 10.1038/30918.
[2]BARABASI A L,ALBERT R,JEONG H.Mean-field theory for scale-free random networks[J].Physica A: Statistical Mechanics and its Applications,1999,272(1): 173-187.DOI: 10.1016/s0378-4371(99)00291-5.
[3]高自友,吴建军,毛保华,等.交通运输网络复杂性及其相关问题的研究[J].交通运输系统工程与信息,2005,5(2): 79-84.DOI: 10.3969/j.issn.1009-6744.2005.02.013.
[4]高自友,赵小梅,黄海军.城市交通网络的复杂性[M].上海: 上海科技教育出版社,2006: 57-64.
[6]CHEN Y Z,LI N,HE D R.A study on some urban bus transport networks[J].Physica A: Statistical Mechanics and its Applications,2007,376: 747-754.DOI: 10.1016/j.physa.2006.10.071.
[7]CHEN Y Z,LI N.Statistical properties of urban ground bus-transport networks from self-avoiding random walks[J].Modern Physics Letters B,2007,21(16): 1027-1040.DOI: 10.1142/s0217984-907013572.
[8]汪涛,许乐,张继,等.城市公交网络的拓扑结构及其演化模型研究[J].公路交通科技,2009,26(11): 108-112,122.DOI: 10.3969/j.issn.1002-0268.2009.11.021.
[9]SEN P,DASGUPTA S,CHATTERJEE A,et al.Small-world properties of the Indian railway network[J].Phys Rev E Stat Nonlin Soft Matter Phys,2003,67(3Pt2): 036106.DOI: 10.1103/PhysRevE.67.036106.
[10]SEATON K A,HACKETT L M.Stations,trains and small-world networks[J].Physica A: Statistical Mechanics and its Applications,2004,339(3): 635-644.DOI: 10.1016/j.physa.2004.03.019.
[11]JIANG B.A topological pattern of urban street networks: Universality and peculiarity[J].Physica A: Statistical Mechanics and its Applications,2007,384(2): 647-655.DOI: 10.1016/j.physa.2007.05.064.
[12]RUI Y,BAN Y,WANG J,et al.Exploring the patterns and evolution of self-organized urban street networks through modeling[J].The European Physical Journal B,2013,86(3): 86-74.DOI: 10.1140/epjb/e2012-30235-7.
[13]ANGELOUDIS P,FISK D.Large subway systems as complex networks[J].Physica A: Statistical Mechanics and its Applications,2006,367(4): 553-558.DOI: 10.1016/j.physa.2005.11.007.
[14]CHANG K H,KYUNGSIK K H,OSHIMA S M.Yoon.Subway Networks in Cities[J].Journal of the Korean Physical Society,2006(2),48: 143-145.
[15]黄少辉.城市轨道交通网络演化模型[D].上海: 上海海事大学,2013: 23-40.
[16]王焱,杨超.上海市轫道交通网络的复杂网络特性研究[J].城市轨道交通研究,2009,12(2): 33-36,55.DOI: 10.3969/j.issn.1007-869X.2009.02.009.
[17]赵召胜,王燚.上海市轨道交通网络演化特征分析[J].城市道桥与防洪,2012(9): 1-5,11.DOI: 10.3969/j.issn.1009-7716.2012.09.004.
[18]BONDY J A,MURTY U S R.图论及其应用[M].吴望名,李念祖,译.科学出版社,1984: 15-26.
Comparison of Topology Structures of Mass Transit Networksin Shanghai, Beijing and Guangzhou Based on Space P
ZHOU Xizhao1,2,ZHI Luping1,MA Hongwei3
(1. School of Economics and Management, Shanghai Maritime University, Shanghai 201306,China; 2. School of Management, University of Shanghai for Science and Technology, Shanghai200093, China; 3. School of Business, Shanghai Dianji University, Shanghai 201306, China)
AbstractAccording to the physical structure and operating characteristics, a space P topology mode is established for the metro networks in Shanghai, Beijing, and Guangzhou. Based on the complex network theory, the topology structure features of urban rail transit network in the three cities are analyzed using statistical indicators. Differences in the network topology structure features in space P is compared. The degree distribution, average shortest path, clustering coefficients of the three urban rail transit networks are compared. The relation between clustering coefficient and degree for the three cities are studied and no definite pattern is found. The results indicate that the metro networks in Shanghai, Beijing and Guangzhou have high clustering coefficients and small degree, meaning that the metro systems have complex network characteristics and are all small word networks in space P. This study helps reveal the network properties of metro systems.
Keywordsmass transit network; topological structure; space P
收稿日期:2015-12-21
基金项目:国家自然科学基金面上基金项目资助(61273042);上海市教育委员会科研创新项目资助(12ZZl47)
作者简介:周溪召(1964-),男,教授,博士,主要研究方向为交通规划与管理,E-mail: xizhaozhou@163.com
文章编号2095-0020(2016)02-0105-06
中图分类号F 512.6
文献标志码A
※: http:∥www.askci.com/news/201307/01/01964886675.shtml

