基于灰色关联度的桩基础选型的研究
方 俊
(昆明理工大学 建筑工程学院,云南 昆明 650000)
基于灰色关联度的桩基础选型的研究
方俊
(昆明理工大学建筑工程学院,云南昆明650000)
[摘要]桩基础是当今常用的基础形式之一,而桩基础的选型在基础工程中则显得尤为重要。若桩基选型不合理,将导致企业蒙受损失。本文应用灰色关联度理论,有效地解决了桩基优化问题,为企业在今后从事项目活动中提供参考及借鉴。
[关键词]桩基础;灰色关联度;桩基优化
[DOI]10.13939/j.cnki.zgsc.2016.04.136
1工程概况
天瑞万象城,位于西双版纳景洪市,总投资约为4亿元,周边居住环境成熟,坐拥多个知名别墅居住区及住宅社区,该项目建筑面积21万平方米。由于周边地质情况复杂,桩基方案经过专家反复考察及论证,最终提出了四种桩型可供选择:预制砼静压桩、钻孔灌注桩、沉管灌注桩、人工挖孔桩。由于考虑到预制砼静压桩的初期成本较低,且便于业主方管理,最终选择了该种方案,但由于该地区地基情况较为复杂,从而在施工过程中出现了以下几个问题:
(1)土质较硬的区域在压桩时出现部分预制管桩断裂、移位等情况。无法完全将桩压至设计标高,达不到设计承载力的要求。
(2)当地没有预制管桩厂,管桩需要从距离景洪市500多千米的玉溪市运输过来,造成预制管桩运输不及时,打桩工作效率低下,无法按期完工,且造成了大量工人的窝工。施工单位无法正常进行接下来的主体施工,多次催促桩基工程进度未果,给业主方造成了不必要的索赔。
在现代的桩基础工程实践中,开发了大量的桩型,对于某一项具体的工程来说,桩型的选择是一个需要慎重对待的问题。桩基设计应该尽可能选用技术性能更好、经济效益更高以及更适合现有施工条件的桩型。[1]桩基选型常采用的方法为“主要因素法”和“模糊综合评价法”。“主要因素法”是考虑初期成本最低或是工期最短的方案作为“最优”方案,但这必将导致无法定量的指标被忽略,从而造成最终方案并非真正的“最优”方案。“模糊综合评价法”是构建一个模糊矩阵,并通过专家确定权重值。综合模糊评价为了确定指标隶属度,在指标特征化中,使一些本来确定的白化值变成区间模糊值,由此出现误差,甚至导致反结论。[2]
本文通过灰色系统理论中的灰色关联度,对桩桩基础的方案进行分析和优选,并引用层次分析法确定各评价指标的权重值,使得权重方面更加具有客观性,以此作为评判桩基方案优劣的决策依据。
2应用灰色理论方法进行桩基选型
2.1评价指标的量化
分别从造价、工期、安全、环境、可靠性及其复杂程度6个方面对桩基础的四种类型进行评价。其中造价和工期为定量指标,可按实际要求计取,而其余指标为定性指标,由各经验丰富的专家将其进行量化,以0~1之间的数值记取,如表1所示。
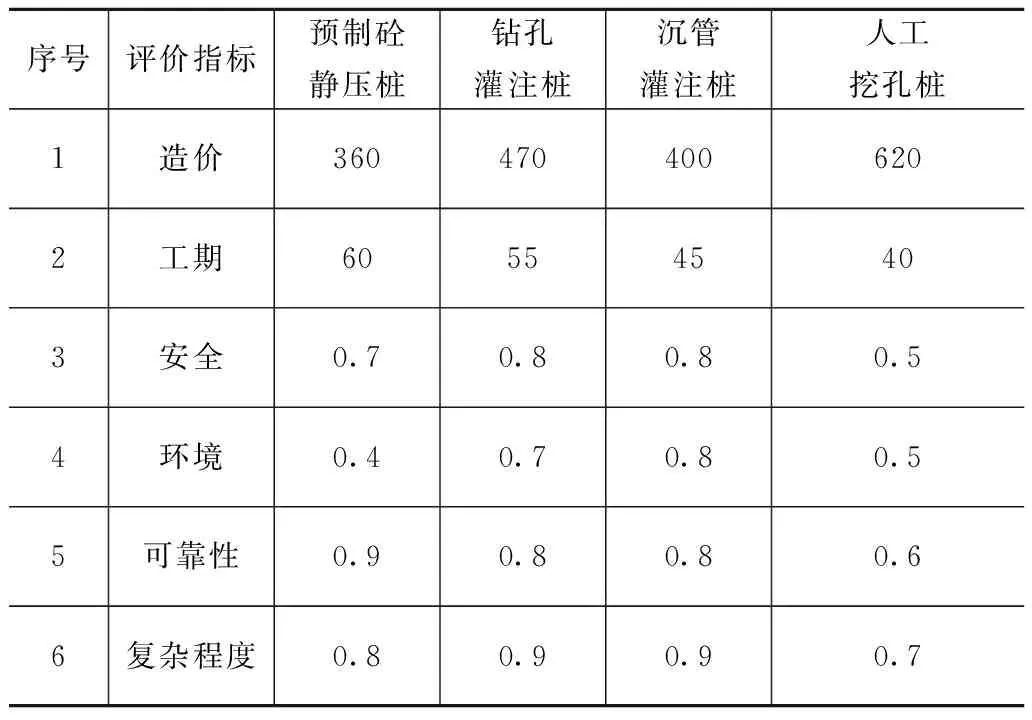
表1 四种桩基础选型的量化指标表
表1所示序号1、2、4、6为成本型指标,即越小越优型。在一定范围内如果该值越小,则效用越大。而序号3、5为效益型指标,即越大越优型,其值越大则效用越大。
2.2评价目标与备选方案
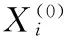
2.3数据的无量纲化
为保证方案间相同指标的可比性,需要对原始数据进行无量纲化处理,即令
(1)
(2)
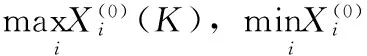
根据表1,分别代入(1)式和(2)式对其进行数据的无量纲化,结果如表2所示。表2中参考数据列第k数据由各方案中最大值构成,全部为1。
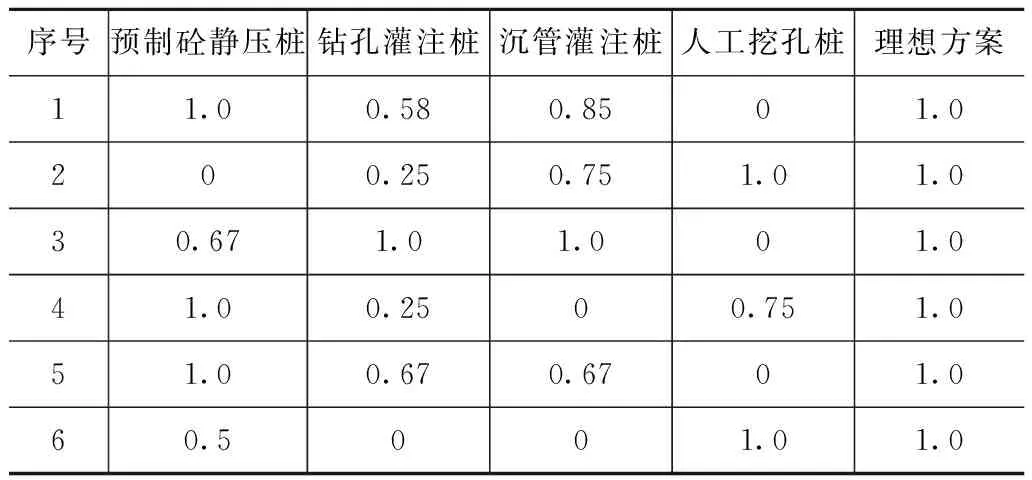
表2 比较数据列和参考数据列的数据无量纲化
2.4关联系数计算
以理想方案m个评价指标的无量纲值构成参据列X0(K)(k=1,2,…,m),以各备选方案的m项指标无量纲值构成比较列Xi(K)(i=1,2,…,n;k=1,2,…,m)。然后按下式计算各参考数据列和比较数据列的关联系数:
(3)
式中,Δoi(K)为参考数据与第i个比较数据列在第k项指标处的绝对差(表3),Δoi(K)=|X0(K)-XI(K)|,ζi为x0与xi在第k项指标处的关联系数,ρ为分辨系数,ζ取0~1之间。
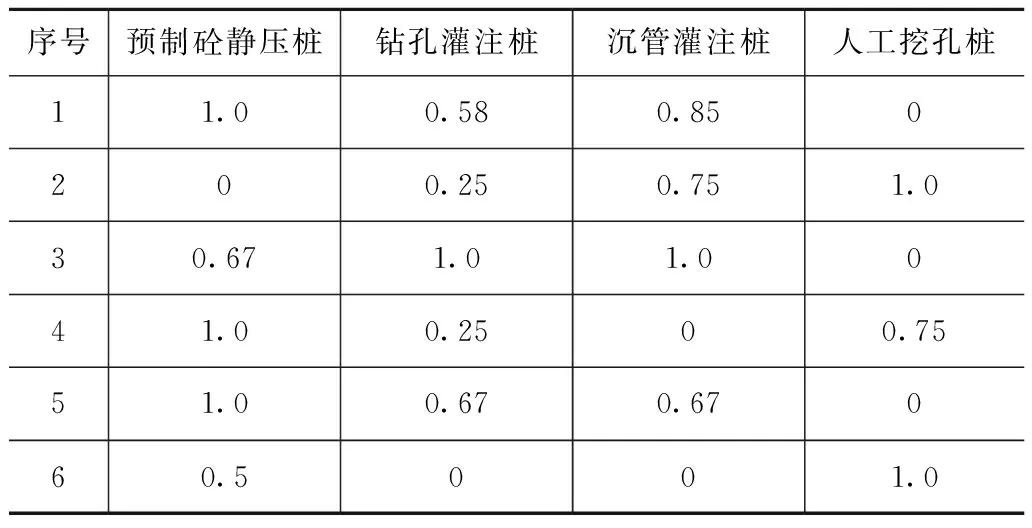
表3 绝对值差的结果
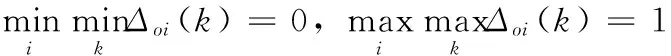
(4)
由此可计算关联系数,结果如表4所示。
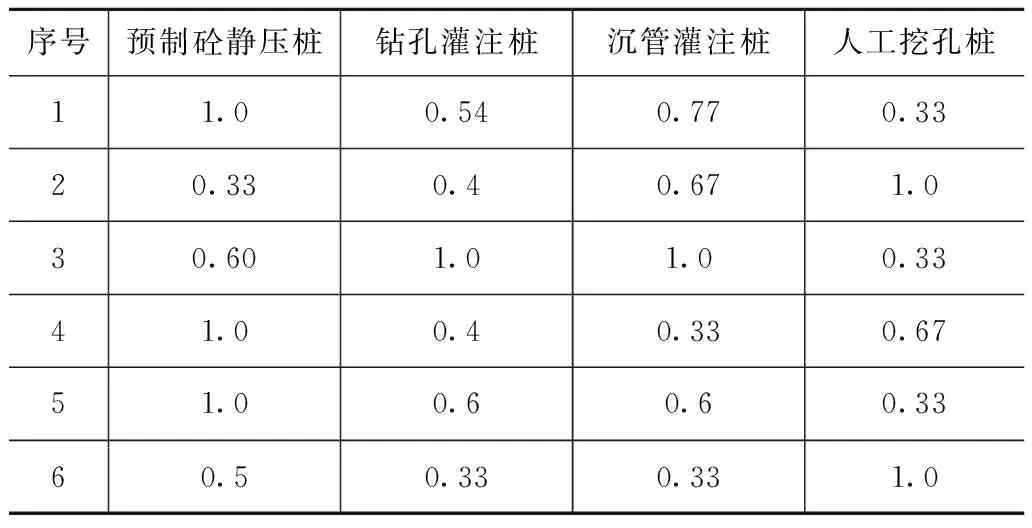
表4 关联系数计算结果
2.5计算关联度
最终由各项指标在方案决策中的影响程度不同,应该对关联度进行加权计算:
(5)
式(5)中,w为各指标在方案决策中的权重。
3关于权重的确定
在我国以往的研究中,采用模糊综合评判法来进行桩基选型,其权重值主要是通过人的主观来判断的,当因素太多时,很难分配权数,从而造成了所选的方案并非“最优”方案。为了使得评价目标的权重值更加客观准确,本文引用层次分析法(AHP)来进行确定各评价指标的权重值。该方法由美国著名运筹学家萨蒂(T.L.Satty,1998)提出把定性与定量分析结合起来的层次权重决策分析方法,具有分层渐进的特点,由于它在处理复杂决策问题上的实用性和有效性,很快在世界范围内得到了广泛应用。[3]
层次分析法适用于多准则、多目标的复杂问题的决策分析,层次分析法的基本内容如下:首先根据问题的性质和要求,提出一个两两对比的方法确定相应上一目标层的权数,层层分析下去,直到最后一层,即能给出所有的因素相对于总目标而言,按照其重要性程度进行的一个排序。
首先建立层次结构图,此结构图分为三个层次:目标层、标准层及决策层。如下图所示。
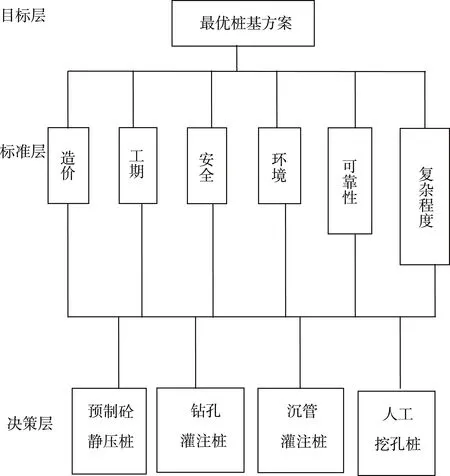
层次结构图
由上图可知,为了得到最佳的桩基础方案,是分别从造价、工期、安全性、环境污染、可靠性及其施工复杂程度方面来进行衡量的。这就需要求出标准之间的权重值。由表5可知各标准两两比较求得相对权重值。
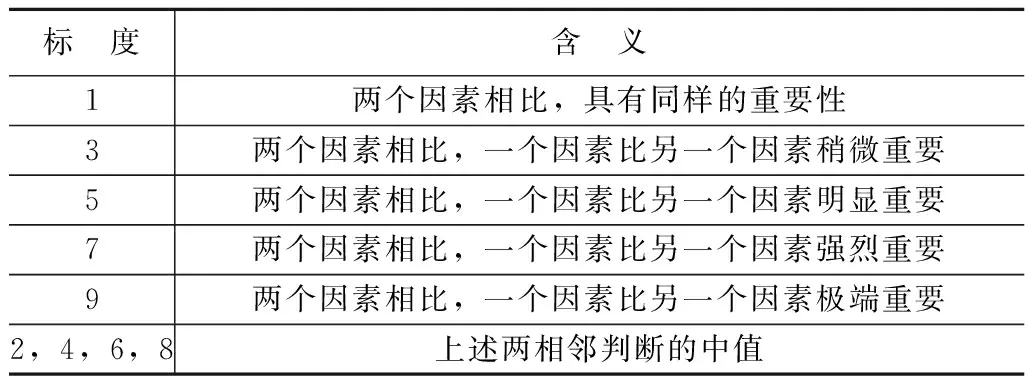
表5 相对重要性标度
根据每个标准间的相对权重,将这6个标准进行两两比较,得出标准之间两两比较矩阵如表6所示。
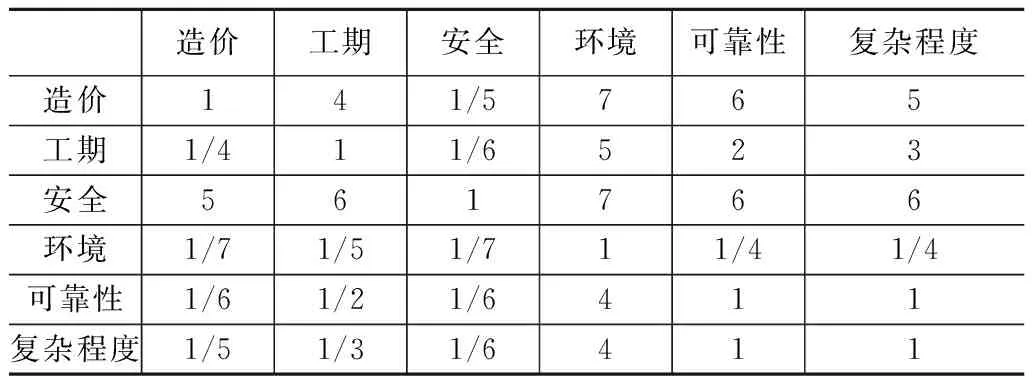
表6 标准之间的两两比较矩阵
造价与工期之间相比,造价的重要程度比工期是在稍微与明显之间,故定a12=4,造价与安全性相比较,安全性比造价明显重要,则定a13=1/5,环境、可靠性及复杂程度相对于造价,造价更为重要,则我们分别令a14=7,a15=6,a16=5,由于标度的倒数定义,可知a21=1/4,a31=5,a41=1/7,a51=1/6,a61=1/5,显然,每个方案与自己相比其重要程度肯定是相同的,故a11=a22=a33=a44=a55=a66=1。求出两两比较矩阵每一列的总和,两两比较矩阵的每一元素除以其相对应列的总和,所得商为标准两两比较矩阵,并计算出标准两两比较矩阵的每一行的平均值,该值就是各指标的权重值。通过标准之间的两两比较矩阵,求得标准的特征向量为(0.253,0.114,0.463,0.030,0.070,0.070),即造价权重为0.253,工期权重为0.114,安全性权重为0.463,环境影响权重为0.030,可靠性权重为0.070,复杂程度权重为0.070。
为了防止判断结果与实际情况偏差过大,需要对评价的矩阵中每一个权重值进行一致性检验。
由标准之间的两两比较矩阵与权重值之乘积,所得的向量为赋权和向量。如下所示:

由每个赋权和向量的分量分别除以对应特征向量的分量,得(7.04,6.61,7.28,6.33,6.23,6.09),则评价矩阵最大特征根得
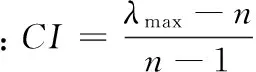
CI=0.119。
计算一致性率CR则需引入修正值RI,当n=6时,RI=1.24,则
由于CR≤0.1,则认为两两比较矩阵之间的一致性可以接受,其相应求得的特征向量有效。
4关联度的加权计算
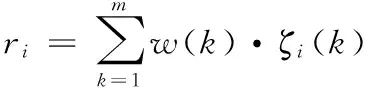
预制砼静压桩=0.253×1.0+0.114×0.33+0.463×0.6+0.03×1.0+0.07×1.0+0.07×0.5=0.703
钻孔灌注桩=0.253×0.54+0.114×0.40+0.463×1.0+0.03×0.4+0.07×0.6+0.07×0.33=0.722
沉管灌注桩=0.253×0.77+0.114×0.67+0.463×1.0+0.03×0.33+0.07×0.6+0.07×0.33=0.807
人工挖孔桩=0.253×0.33+0.114×1.0+0.463×0.33+0.03×0.67+0.07×0.33+0.07×1.0=0.465
根据灰色系统理论的关联度原理,四种方案的优化顺序依次是:沉管灌注桩>钻孔灌注桩>预制砼静压桩>人工挖孔桩。所以最终选择沉管灌注桩作为本工程的“最优”方案。
5结论
在本案例中,之所以在施工过程中出现了各种问题,是由于选择了预制砼静压桩的方案所造成的,最终通过本文分析,选择采用沉管灌注桩,根据其施工工艺,避免了管桩断裂的问题,而且由于是现场灌注,也不可能存在由于运距远所造成的工期拖延。
通过引入灰色关联度的方法,不仅解决了“主观因素法”中容易忽略无法定量指标的问题,而且克服了模糊综合评判法中对于权重确定的主观性。
结合实际工程情况,桩基础选型量化指标表内的系数是不断变化的,我们应根据不同的环境选择合理的桩基类型。在其他项目中,选择预制砼静压桩方案将可能优于沉管灌注桩,不能仅仅看到初期成本低,就片面地选择成本最低的方案。该方法在保证桩基结构安全性的基础上,降低了工程造价,并且极大地缩短了工期,使企业在项目活动中取得良好的经济效益。
参考文献:
[1]张忠苗.桩基工程 [M].北京:中国建筑工业出版社,2008.
[2]康彦民.公路工程建设项目的综合经济评价与决策分析 [J].公路交通科技,2001(2):87.
[3]胡新萍,王芳.模糊综合评价法在既有建筑节能改造评估中的应用 [J].建筑技术,2014(9):95-96.

