随机地震动输入模型研究及渡槽抗震分析

王　舟，吴林强，刘增辉

(三峡大学 a.水利与环境学院; b.湖北省防灾减灾重点实验室，湖北 宜昌　443002；)

随机地震动输入模型研究及渡槽抗震分析

王舟a，b，吴林强a，b，刘增辉b

(三峡大学a.水利与环境学院;b.湖北省防灾减灾重点实验室，湖北 宜昌443002；)

摘要：在平稳地震动过程的Kanai-Tajimi模型和Clough-Penzien模型的基础上，分别建立了2种全非平稳地震动加速度过程的广义演变谱模型。根据我国现行的《水工建筑物抗震设计规范》(DL 5073—2000)，确定了2种广义演变谱模型的参数值。应用非平稳随机过程模拟的谱表示-随机函数方法，分别生成了基于2种广义演变谱的全非平稳地震动代表性时程集合，并进行了二阶数值统计值的对比分析。同时，通过代表性时程集合的平均反应谱与规范反应谱的拟合比较，发现K-T(Kanai-Tajimi)广义演变谱模型更适用于水工建筑物抗震设计。最后，将K-T广义演变谱模型与概率密度演化理论相结合，对渡槽结构进行了随机地震反应和抗震可靠度分析。

关键词：全非平稳地震动；水工抗震；概率模型；渡槽；概率密度演化理论

1研究背景

地震地面运动是一个典型的非平稳随机过程，对于水工建筑物，如重力坝、渡槽等这类重要工程几乎都要进行地震动时程分析[1]。

在地震工程中，一般采用功率谱密度函数来描述平稳地震动过程，而采用演变功率谱密度函数(简称演变功率谱)来描述全非平稳地震动过程。在平稳地震动过程的功率谱模型研究中，Housner[2]首先采用白噪声模型来描述地震地面运动，Kanai[3]和Tajimi[4]提出了能较好反映场地土特性的平稳过滤白噪声模型，即著名的Kanai-Tajimi模型。由于Kanai-Tajimi模型假定基岩地震动加速度为白噪声过程，不能反映基岩地震动的频谱特性，此外，在零频率处不能满足位移和速度是有界的条件。为了克服Kanai-Tajimi模型的不足，国内外一些学者提出了多种改进模型，如胡聿贤模型[5]、Clough-Penzien模型[6]等。在非平稳地震动过程的演变功率谱模型研究中，Deodatis[7]提出了一类非平稳地震动加速度过程的演变功率谱模型，但该模型参数识别困难，进一步地，文献[8]提出了一类全非平稳地震动加速度过程的广义演变谱模型。此类模型充分考虑了地震动在强度和频率2方面都具有非平稳性的特征，而目前地震工程中广泛采用只考虑强度非平稳随机过程模型进行地震动的人工模拟，这对结构的非线性地震响应和损伤破坏有较大的影响[9]。因此，建立一种既考虑强度非平稳又考虑频率非平稳的全非平稳地震动模型对工程应用具有重大意义。

本文在文献[8]基础上，以平稳地震动过程的K-T(Kanai-Tajimi)谱模型和C-P(Clough-Penzien)谱模型为例，分别建立了两种全非平稳地震动加速度过程的广义演变谱模型。同时，应用文献[10]中非平稳随机过程模拟的谱表示—随机函数方法，分别生成了2种全非平稳地震动加速度过程的代表性时程集合，并进行了二阶数值统计值的对比分析。通过代表性时程集合的平均反应谱与规范反应谱的拟合误差分析，发现基于K-T的广义演变谱模型更适用于水工建筑物抗震设计的要求。最后，结合概率密度演化理论[11-12]，进行了渡槽结构的随机地震反应分析与抗震可靠度计算。

2非平稳地震动过程的演变谱模型

在平稳地震动随机过程模型中，K-T谱和C-P谱是2种经典的功率谱模型，在地震工程中应用广泛。K-T谱考虑了场地土层特性对地震动频谱特征的影响，是一种单重过滤白噪声模型。C-P谱在K-T谱的基础上考虑了基岩的动力特性，是一种双重过滤白噪声模型。

在非平稳地震动随机过程模型中，文献[8]在强度调制的非平稳地震动模型基础上，发展了一类强度和频率调制的全非平稳地震动过程的广义演变谱模型。其基本思想是将平稳地震动加速度过程的功率谱拓展或扩展为一类广义的时变功率谱。下面，根据平稳地震动加速度过程的K-T谱和C-P谱，可以给出相应的全非平稳地震动加速度过程的广义演变谱模型。

对于K-T谱模型，其对应的全非平稳地震动加速度过程的广义演变谱(双边谱)为

(1)

式中：t为时间变量；ω为频率变量；参数ωg(t)和ζg(t)分别为场地土的频率和阻尼比；参数S0(t)为谱强度因子；A(t)为强度调制函数。

在式(1)中，参数S0(t)可表示为[8]

(2)

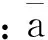
对于C-P谱模型，其对应的全非平稳地震动加速度过程的广义演变谱(双边谱)为

(3)

式中：ωf(t)和ζf(t)为基岩的过滤参数，一般地，过滤参数ωf(t)=0.1ωg(t)和ζf(t)=ζg(t)。

在上述2种广义演变谱的表达式中，反映频率非平稳特性的参数ωg(t)和ζg(t)分别可表示为[8]：

(4)

(5)

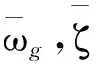
对于强度调制函数A(t)，本文建议取为[13]

(6)

式中：c为地震动峰值加速度出现的时间；d为控制A(t)形状的指数。参数c和d按地震动持续时间T来确定，与场地类别有关。

3非平稳过程模拟的谱表示—随机函数方法

(7)

式中：ωn=nΔω，Δω为离散的频率步长；N为截断项数；Sg(t,ωn)为双边的演变谱密度函数，满足Sg(t,ω0)=Sg(t,0)=0的条件。

在式(7)中，标准正交随机变量{Xn,Yn}(n=1,2,…,N)满足如下的基本条件：

(8)

(9)

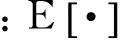
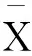
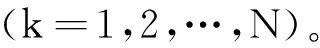
(10)

4非平稳地震动过程模拟的对比分析

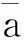
表1　广义演变谱参数的取值

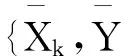
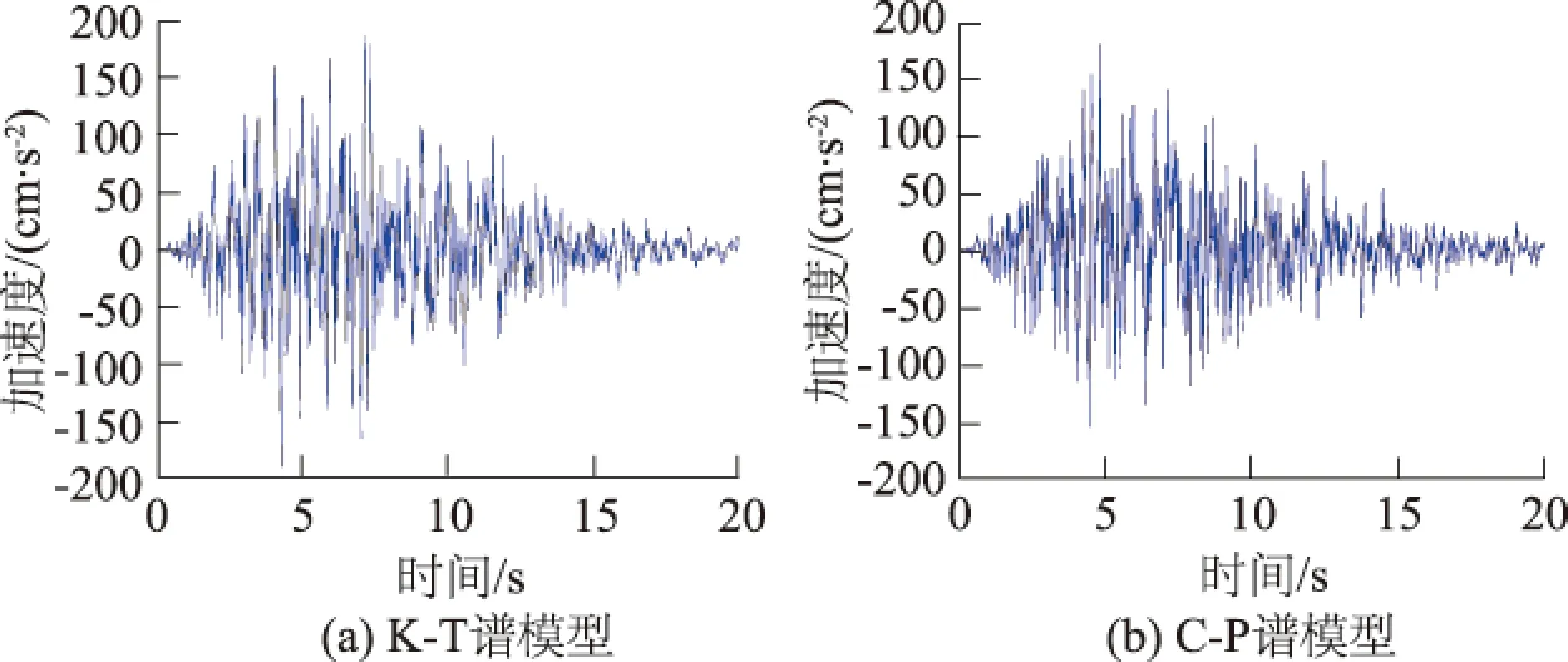
图1　非平稳地震动加速度过程的代表性时程曲线Fig.1　Typical time-histories of non-stationaryground motion acceleration

图2为610条非平稳地震动加速度时程的均值、标准差与目标值比较。

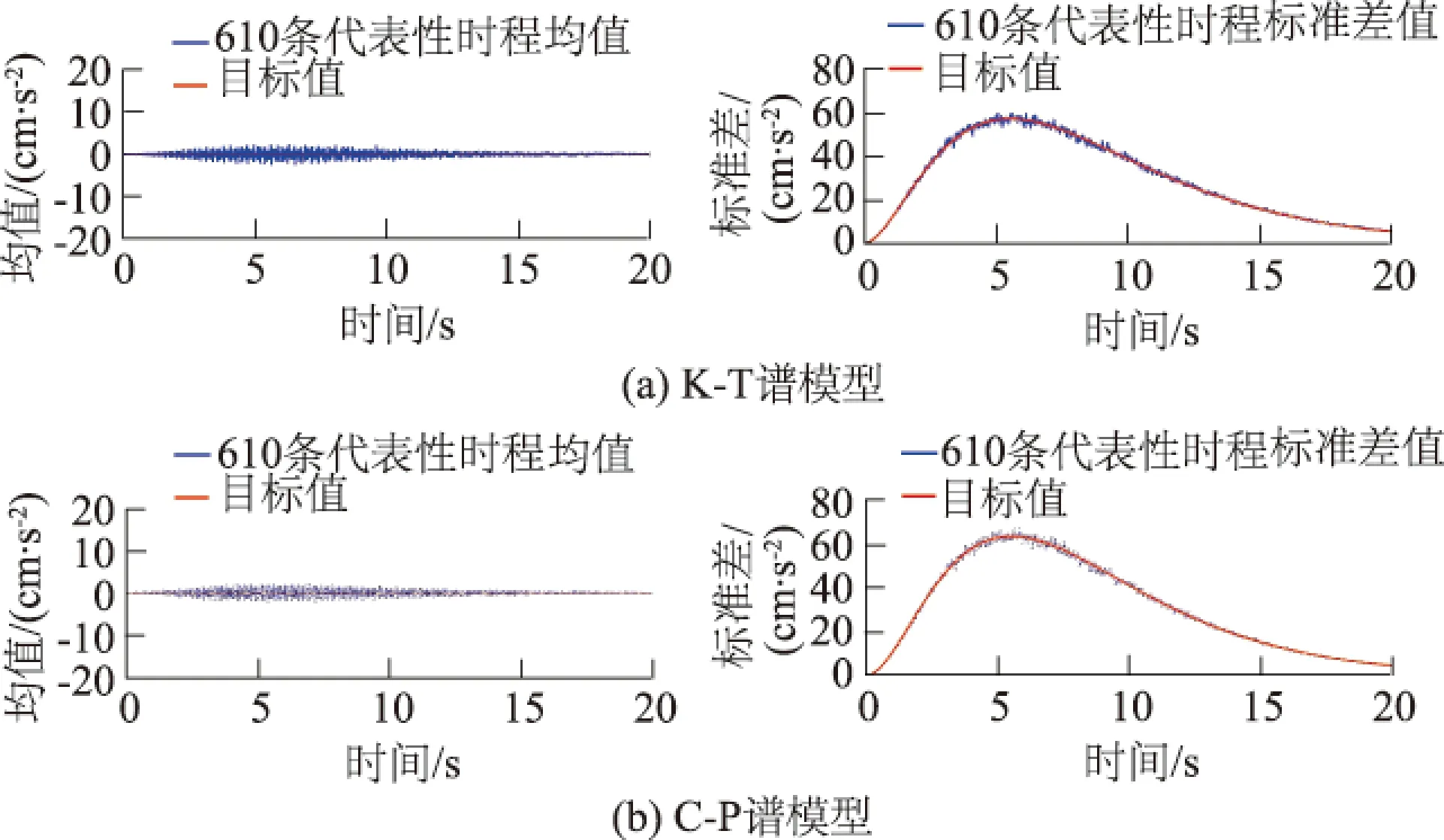
图2　不同模型下均值、标准差的时程曲线比较Fig.2　Comparison of time-history curves of mean value and standard deviation in different models

从图2可知，两者的符合程度较为理想，这表明，在二阶数值统计意义上，610条代表性时程的总体特性与目标值相符，K-T广义演变谱模型和C-P广义演变谱模型与目标值的拟合误差均比较接近。因此，从二阶数值统计特征上看，K-T广义演变谱模型和C-P广义演变谱模型是基本一致的。

根据《水工建筑物抗震设计规范》(DL5073—2000)[14]，对于水工混凝土建筑物(如渡槽结构)，规范中反应谱最大值的代表值βmax=2.25，反应谱下限值的代表值βmin=0.45。结构阻尼比取0.05，规范给出的设计反应谱中曲线段的表达式为

(10)

式中：Tg为场地特征周期，对于场地类别Ⅱ，Tg=0.30s；T0为结构基本自振周期。

图3给出了用本文方法生成的610条代表性时程的均值反应谱β值与规范反应谱β值的比较。

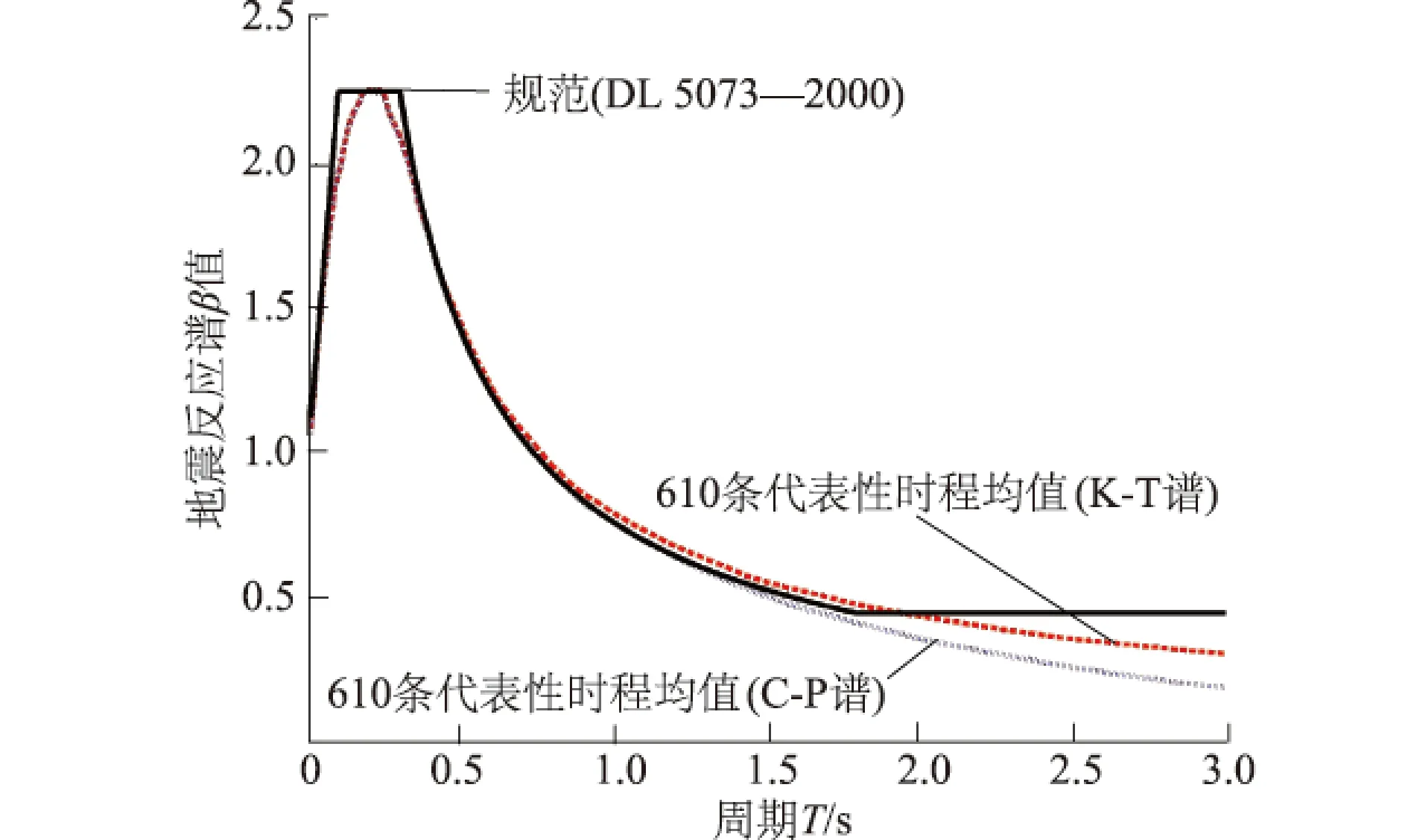
图3　时程总体的反应谱与目标反应谱的比较Fig.3　Comparison of response spectrum among K-T model,C-P model, and the Code

从图3中可知，在反应谱的曲线下降段末端之前部分，两者的符合程度十分理想。从与规范反应谱的拟合误差来看，K-T广义演变谱模型比C-P广义演变谱模型的拟合误差更小些。

需要指出的是，尽管平稳地震动过程的K-T模型存在不足，但从基于K-T和C-P的广义演变谱所生成的代表性时程集合来看，两者的二阶数值统计值与目标值均十分接近，且两者的拟合误差几乎一致。此外，从水工建筑物抗震设计来看，基于K-T的广义演变谱能够更加符合规范要求，这是由于K-T谱在低频部分估计过高，而这种低频部分的过高估计正好能够弥补《水工建筑物抗震设计规范》中反应谱对长周期部分的人为提高。为此，在进行水工建筑物抗震设计时，采用基于K-T的广义演变谱模型较为适合。

5工程实例及分析

本文工程实例参照文献[15]，某简支结构水电站引水渡槽，全长为440.0m，单跨长40.0m，槽身断面是矩形单槽，槽底净宽为8.4m，槽身高为6.4m，其设计水位为4.61m，侧墙厚度为0.5m，槽底厚度为0.55m；渡槽槽墩是圆端型高空心墩结构，槽身与槽墩之间设置盆式橡胶支座；本文选取中间跨来计算，其墩高为48m，特点是上小下大，上端壁厚度为0.5m，下端壁厚度为0.822m；各个力学参数取值，槽墩为钢筋混凝土结构，其混凝土强度等级为C30，其密度2 500kg/m3，弹性模量为30GPa，泊松比为0.167，阻尼比为0.05；槽身为钢筋混凝土结构，其混凝土强度等级为C50，其密度为2 500kg/m3，弹性模量为35GPa，泊松比为0.167，阻尼比为0.05；水体密度为1 000kg/m3。结构的有限元模型如图4所示。

图4　渡槽有限元模型Fig.4　Finite element model of aqueduct

图5　跨中结点位移均值和标准差曲线Fig.5　Mean values and standard deviations of nodedisplacement in the middle of aqueduct span

本文计算：当渡槽内为设计水位4.61m，利用豪斯纳尔弹簧简化模型[16]来考虑水体与渡槽间的相互作用。地震沿槽身顺向输入，主要分析了在K-T广义演变谱模型的地震动作用下，渡槽结构跨中节点位移的概率变化情况。

图5给出了渡槽跨中节点位移的均值和标准差，其中均值大体趋于0。图6分别给出了渡槽跨中节点位移在3，6和9s3个不同典型时刻的概率密度函数曲线，可以看出渡槽跨中节点位移的概率密度函数曲线在随时间演化。图7给出了渡槽跨中节点位移的等概率密度曲线，可以看出在9～12s内不同渡槽跨中节点位移大小的分布情况。图8中给出了概率密度的演化曲面，该曲面表明概率密度函数渡槽跨中节点位移随时间的不同分布和演化进程。

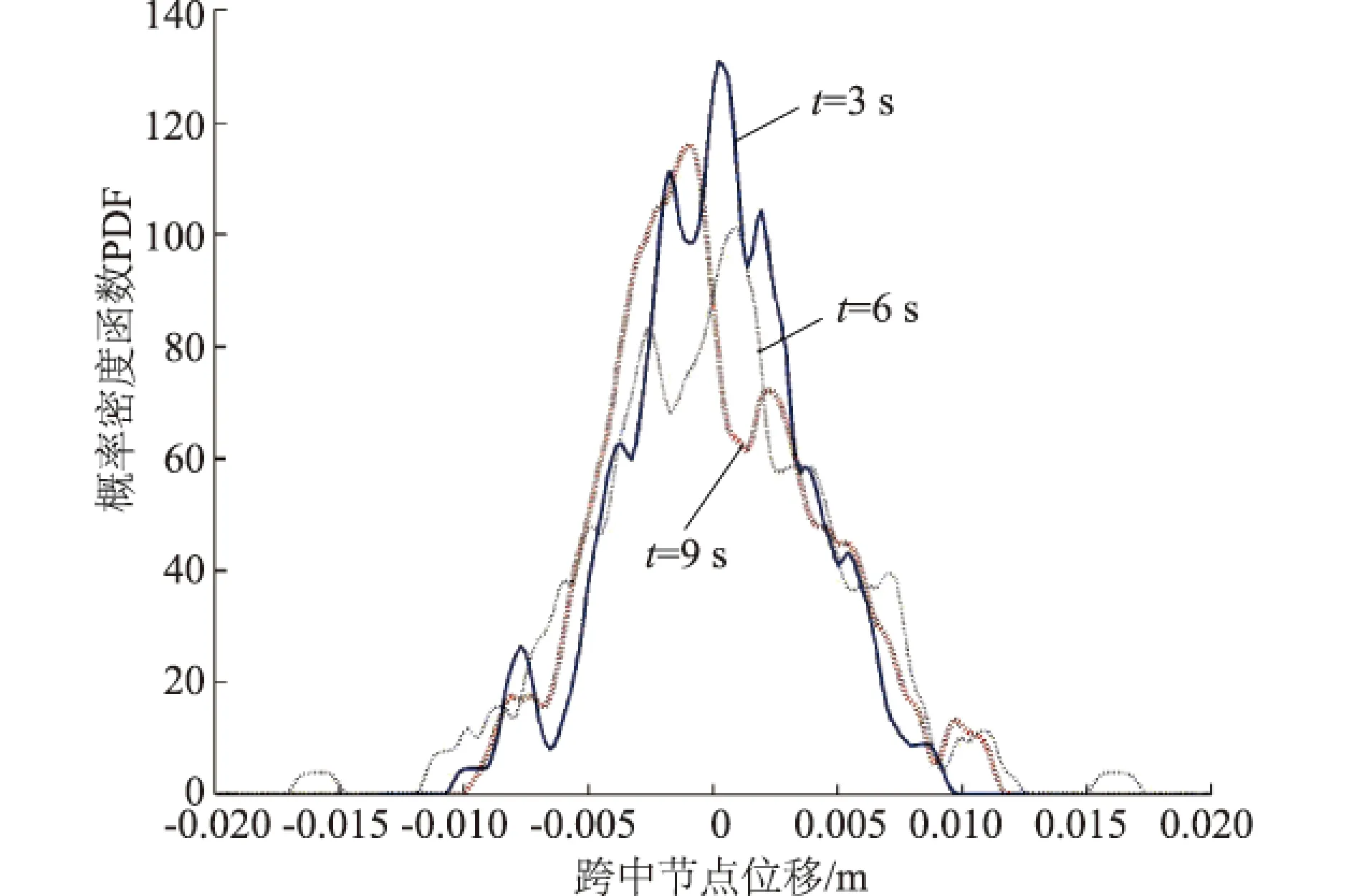
图6　典型时刻的概率密度曲线Fig.6　Probability density function attypical time instants

图7　等概率密度线Fig.7　Curves of equal probability density function

图8　等概率密度面Fig.8　Surfaces of equal probabilitydensity function

再根据等价极值事件的思想[17]，构造渡槽跨中节点位移的等价极值事件，计算得到渡槽跨中节点位移的极值分布概率密度函数和概率分布曲线，对比图如图9所示。即可得到渡槽在以跨中节点位移为失效控制模式，不同失效界限值对应的抗震可靠度。

从图9(a)中可以看出：K-T广义演变谱模型的地震动作用于渡槽所产生的跨中节点位移在增大的过程中，其概率密度函数在一定的范围呈现先增大后减小的趋势。从图9(b)中可以看出：以跨中节点位移为失效准则，当其界限值us=0.01m时，可靠率为33.25%；当其界限值us=0.015m时，可靠率为93.25%；当其界限值us=0.02m时，可靠率为100%。若以不超过5%为失效概率，当其界限值us=0.02m时，渡槽是可靠的。

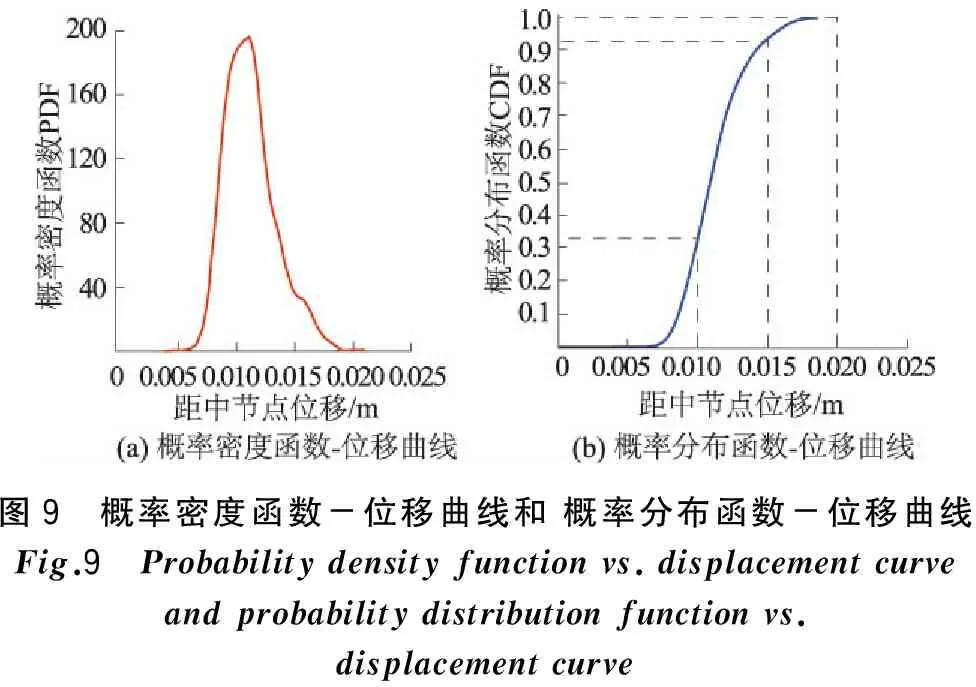
图9 概率密度函数-位移曲线和概率分布函数-位移曲线Fig.9 Probabilitydensityfunctionvs.displacementcurveandprobabilitydistributionfunctionvs.displacementcurve

6结论

本文根据我国现行的《水工建筑物抗震设计规范》(DL5073—2000)，应用非平稳随机过程模拟的谱表示-随机函数方法，以全非平稳地震动加速度过程的广义演变谱模型为基础，建立了水工建筑物抗震设计所用的2种地震动概率模型。

对比2种地震动概率模型可以得出以下结论：

(1) 在二阶数值统计意义上，610条代表性时程的总体特性与目标值相符，K-T广义演变谱模型和C-P广义演变谱模型与目标值的拟合误差均比较接近，且K-T广义演变谱模型和C-P广义演变谱模型是比较一致的。

(2) 在场地类别Ⅱ，模型参数的取值如表1所示的情况下，与规范反应谱的拟合误差来看，K-T广义演变谱模型比C-P广义演变谱模型的拟合误差更小些。为此，在进行水工建筑物抗震设计时，采用基于K-T的广义演变谱模型较为适合。

(3) 在可靠度方面，若以不超过5%为失效概率，且以跨中节点位移为失效准则，当其界限值为0.02m时，可以保证在设防地震为8度，第Ⅱ类场地下，渡槽在K-T广义演变谱模型设计地震作用下是可靠的。

致谢:三峡大学土木与建筑学院刘章军教授对本文进行了大力指导及悉心修改，在此表示最衷心的感谢。

参考文献：

[1]陈厚群,吴胜兴,党发宁.高拱坝抗震安全[M].北京:中国电力出版社,2011.

[2]DOUGLASJ,AOCHIH.ASurveyofTechniquesforPredictingEarthquakeGroundMotionsforEngineeringPurposes[J].SurveysinGeophysics, 2008, 29(3): 187-220.

[3]KANAIK.Semi-empiricalFormulafortheSeismicCharacteristicsoftheGroundMotion[J].BulletinoftheEarthquakeResearchInstitute,UniversityofTokyo, 1957, 35(2): 308-325.

[4]TAJIMIH.AStatisticalMethodofdeterminingthemaximumresponseofaBuildingStructureduringanEarthquake[C]∥ProceedingsoftheSecondWorldConferenceonEarthquakeEngineering.TokyoandKyoto,Japan, 1960,(2): 781-798.

[5]胡聿贤,周锡元.弹性体系在平稳和平稳化地面运动下的反应[C]∥中国科学院土木建筑研究所地震工程研究报告集(第一集).北京:科学出版社,1962:33-55.

[6]CLOUGHRW,PENZIENJ.DynamicsofStructuresSecondEdition(Revised) [M].NewYork:ComputersandStructures,Inc., 2003.

[7]DEODATISG.Non-stationaryStochasticVectorProcesses:SeismicGroundMotionApplications[J].ProbabilisticEngineeringMechanics, 1996, 11: 149-168.

[8]刘章军,王磊,但庆文, 等. 非平稳地震动的广义演变谱模型及在水工抗震中的应用[J]. 水利学报, 2015,46(9):1028-1036.

[9]陈健云,李静,周晶, 等.地震动频谱对小湾拱坝非线性响应的影响[J].振动工程学报,2003,16(2):207-211.

[10]刘章军,曾波,吴林强.非平稳地震动过程模拟的谱表示—随机函数方法[J].振动工程学报,2015,28(3):411-417.

[11]LIJie,CHENJian-bing.StochasticDynamicsofStructures[M].Singapore:JohnWiley&SonsPteLtd, 2009.

[12]李杰,陈建兵.随机动力系统中的概率密度演化方程及其研究进展[J].力学进展,2010,40(2):170-188.

[13]欧进萍,王光远.结构随机振动[M].北京:高等教育出版社,1998.

[14]DL5073—2000，水工建筑物抗震设计规范[S]. 北京：中国电力出版社,2000.

[15]刘章军,方兴.大型渡槽结构随机地震反应与抗震可靠度分析[J].长江科学院院报,2012,29(9):77-81.

[16]徐建国,陈淮,王博，等.考虑流固动力相互作用的大型渡槽地震响应研究[J].土木工程学报,2005,38(8):67-73.

[17]陈建兵,李杰.结构反应的内蕴相关性与可靠度分析[J]. 计算力学学报,2008,25(4):521-528.

(编辑：刘运飞)

Random Ground Motion Input Models and Seismic Analysisof Aqueduct Structure

WANGZhou1，2,WULin-qiang1，2，LIUZeng-hui2

(1.CollegeofHydraulic&EnvironmentalEngineering,ChinaThreeGorgesUniversity,Yichang443002,China；2.HubeiKeyLaboratoryofDisasterPreventionandReduction,ChinaThreeGorgesUniversity,

Yichang443002,China)

Abstract:On the basis of the Kanai-Tajimi model and Clough-Penzien model of stationary ground motion processes, two types of generalized evolutionary spectral models of fully non-stationary ground motion acceleration process are established, respectively. According to the Code for seismic design of hydraulic structures (DL 5073—2000), the parameter values of generalized evolutionary spectral models are identified. Applying the spectral representation and random function method, the representative samples ensemble of fully non-stationary ground motion process for the two generalized evolutionary spectral models are generated, and the comparative analysis of the second-order numerical statistics is carried out. Moreover, through comparing the average response spectrum of representative samples ensemble and response spectrum calculated by the code, it is found that the generalized evolutionary spectral models of Kanai-Tajimi spectrum is more applicable to seismic design of hydraulic structure. Finally, through combining Kanai-Tajimi generalized evolutionary spectral model with probability density evolution method, the random seismic response analysis and reliability evaluation of an aqueduct structure is investigated.

Key words:fully non-stationary ground motion; hydraulic seismic resistance; probability model; aqueduct; probability density evolution

收稿日期：2015-06-03;修回日期：2015-08-16

作者简介：王舟(1990-)，男，湖北汉川人，硕士研究生，主要从事水工结构抗震研究，(电话)15872639067(电子信箱)w_2010@163.com。

doi:10.11988/ckyyb.20150464

中图分类号：TV312;TU352.11

文献标志码：A

文章编号：1001-5485(2016)06-0129-05

2016,33(06):129-133，139