改进免疫算法在无线网络基站选址优化中的应用*

马宝罗，贾振红，覃锡忠，曹传玲，牛洪梅

(1.新疆大学 信息科学与工程学院，新疆 乌鲁木齐 830046；2.中国移动通信集团 新疆有限公司，新疆 乌鲁木齐 830063)

改进免疫算法在无线网络基站选址优化中的应用*

马宝罗1，贾振红1，覃锡忠1，曹传玲2，牛洪梅2

(1.新疆大学 信息科学与工程学院，新疆 乌鲁木齐 830046；2.中国移动通信集团 新疆有限公司，新疆 乌鲁木齐 830063)

摘要:为了最小化网络建设成本、提高用户的服务质量，提出了一种基于矢量距离免疫计算的基站选址问题求解方案。设计了基于矢量距离的抗体浓度计算方法，采用了反学习的种群初始化策略，给出了问题求解的数学模型。主要工作是准确确定基站的位置和数目，以达到建站代价最小、且满足用户覆盖率和系统容量的目的。仿真结果表明：所提算法有更突出的全局搜索能力和快速收敛性，能更好地实现用较低的建站成本满足用户覆盖率和系统容量。

关键词:无线网络；基站选址优化；免疫优化算法；反学习

0引言

在网络规划过程中，基站选址优化是一项灵活且至关重要的问题，被认为是公认的NP-难问题。对3G/4G网络来说，容量和覆盖需要同时来考虑，这就增加了问题的求解难度。如何选取合适的优化算法求解基站选址优化是国内外学者广泛关注的问题。文献[1]研究了应用多目标进化算法求解4G基站规划问题;文献[2]给出了利用量子免疫进化求解了基站和中继站联合优化问题；文献[3，4]分析了基于免疫算法的基站选址问题。这些算法在求解过程中，没有充分考虑各参数之间的相互影响，并且大多数算法不适用于将规划区域按用户密度分成许多子区域的情况,从而导致算法的性能差，求解速度慢等问题。

基站选址问题包括很多的优化参数，被认为是一个多目标优化问题[5]。本文主要考虑两个重要的目标函数：建设成本和覆盖率。主要工作是从候选基站集合中选出基站的准确位置和数目，在满足用户需求的前提下最小化成本。免疫算法在求解多目标优化问题方面有一定的优势，近年来在多领域得到了广泛应用[6～8]。为更好地解决此问题，本文给出了基于矢量距免疫计算的基站选址优化方案。

1基站选址问题的系统模型

由于网络用户的迅速增长和频谱资源的日益短缺，目前面临的主要问题是网络覆盖差、信号不稳定等问题。为解决此类问题，合理的基站建设显得尤为重要，基站建设的合理与否直接影响着网络的性能和后期的优化、维护等工作。本文规定基站规划区域的总面积为S，i,j分别为规划区域S的长度和宽度，其表达式为

S={Xij,i=1,2,…,m;j=1,2,…,n}

(1)

为了验证网络的系统性能，本文主要考虑的两个目标函数描述如下：

第1个目标函数是建设成本:本文采用文献[3]中的表示方法，用基站的个数来表示成本，定义为

(2)

式中N为候选基站的总个数，N0为选中的基站数目。

第2个目标函数为覆盖率：基站的覆盖范围表示基站发射的信号在下行链路所能达到的的最大距离[9]。对服务测试点TPS，为了确保信号服务质量能够满足用户需求，要求测试点接收到的信号强度必须大于某个阈值Sq，本文用规划区域内被覆盖的测试点个数与候选测试点个数的比值定义为网络覆盖率fcov，即

(3)

(4)

式中nTPS为测试点的个数。

2基于矢量距免疫算法的基站选址优化

2.1抗体编码

在基站选址规划过程中，候选站址只存在被选择或未被选择两种情况，因此，本文采用了最常见的二进制编码，将每个候选基站表示为二进制变量ui∈{0,1}，即

(5)

2.2种群初始化

在免疫算法中，最常用的方法是采用随机生成的方式产生初始解[10]。为了得到高质量的初始种群、增加种群的多样性，采用了基于混沌映射机制的反学习种群初始化方法[11]，该方法的步骤描述如下：

首先,随机产生初始化变量x0，j∈ {0,1}且x0,j∉{0.2,0.4,0.6,0.8}；利用混沌映射机制产生初始种群xij为

(6)

然后,利用反学习的方法产生初始种群xi,j相对应的反向解oxi,j，如式(7)所示

(7)

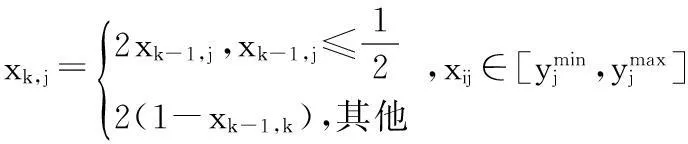
2.3亲和度计算

在种群的评估过程中，一项非常重要的工作就是在综合考虑各种影响因素和已定义的所有目标函数的情况下设计一个亲和度函数[12]。本文中通过综合评估建站成本和覆盖率来反映亲和度函数。亲和度函数定义为

ffit=wcosfcos+wcovfcov

(8)

式中wcos和wcov分别为建站成本权重和覆盖率权重。

2.4抗体浓度

为了增加种群多样性、提高算法的收敛速度，本文采用了基于矢量距的抗体浓度计算方法[13]。根据现代免疫学原理，将抗原看作需要解决的问题、B细胞看作问题的其中一个解、抗体xi对应于解的适应度函数为ffit(xi)。定义抗体xi在种群集合N上的矢量距为

(9)

抗体的浓度定义为

(10)

则抗体xi基于抗体浓度和抗体矢量距的选择概率[14]为

(11)

由式(11)可知，矢量距越大，说明种群N中与xi相似的抗体越少，则抗体xi有更多的机会被选择；反之,亦然。

2.5相关算子设计

为了提高算法的收敛速度和性能，本文使用了克隆变异、种群更新2个算子。

1)克隆变异

首先，对记忆库中的CL个抗体进行克隆增殖。采用文献[7]提出的方法，将CL个抗体按亲和度值由小到大排列，对其中的任意抗体Ai(t)(1≤Ai(t)≤CL),设其克隆规模为qi(t),如式(12)所示，则第t代产生的克隆副本的总个数Q如式(13)所示。然后按变异概率pm对副本种群进行变异

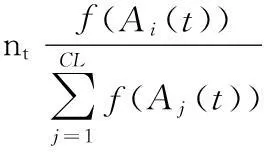
(12)

(13)

式中Int(x)为不小于x的最小整数；nt为根据克隆规模设定的参数，且满足nt>CL；f(x)为抗体x的亲和度。

2)种群更新

计算抗体的亲和度值和浓度值，选出浓度较高的部分抗体，并将剩余的抗体重新初始化，构成新的种群。

2.6改进算法流程

1)设定种群规模为Popsize，记忆库种群规模为CM，克隆母体种群规模CL，迭代次数t。

2)利用混沌反学习法对种群进行初始化生成初始种群A0，并随机取出CM个组成记忆库种群W。

3)计算种群A0中抗体的亲和度值，选出较优的CL个组成克隆母体种群B0，对B0进行克隆增殖并按概率pm进行变异得到种群C0。

4)计算B0∪C0中抗体的亲和度值，并用矢量距法计算其浓度值。

5)从B0∪C0中选出亲和度值较优的抗体去更换记忆库中的原有抗体，更新记忆库。

6)对种群B0∪C0进行更新，产生新的种群。

7)若满足t>tmax，则输出最优解；否则,令t→t+1,转步骤(3)继续执行。

3仿真结果

仿真环境：本文选取一个面积为S(20 km×20 km)的平坦区域进行实验，如图1所示。设定候选基站个数为N=60、候选测试点个数为nTPS=128；选取种群规模为100，最大进化代数为200代。记忆库种群CM为30，克隆母体种群个数CL为60，权重系数α 取0.65。为了得到更好的仿真结果，本文首先讨论了参数变化对算法性能的影响，然后谈论本算法与其他算法的对比实验。

图1　候选基站与测试点分布图Fig 1　Distribution of candidate stations and test point

3.1免疫算法参数调整

设定种群的初始化概率为0.6。这里首先讨论了不同交叉概率(pc)和变异概率(pm)对算法性能的影响。

3.1.1交叉概率调整

为了验证不同交叉概率对算法性能的影响，设定变异概率为0.6的。交叉概率分别取0.2，0.4，0.6和0.8。对算法运行20次，实验结果分别如图2～图4所示。

当交叉概率为0.8时，由图2可知，平均亲和度达到最优值，且收敛速度最快。亲和度值的优劣直接反映着所得解的质量好坏，亲和度越大，说明求出的解质量越高；由图3可知，此时覆盖率达到最大值，且明显高于其他3种情况；由图4可知，方案性价比达到最大值，其值随进化代数的增加上升速度最快，且最先达到收敛状态。

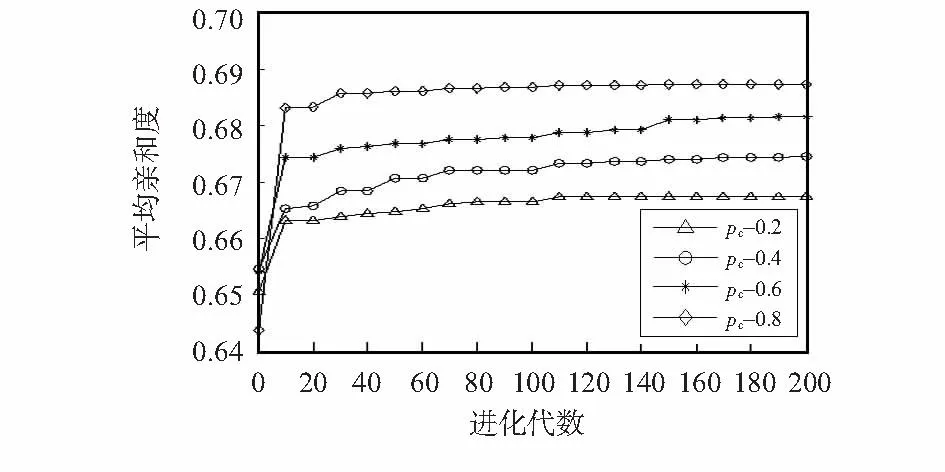
图2　平均亲和度随代数的变化Fig 2　Average affinity change with algebra

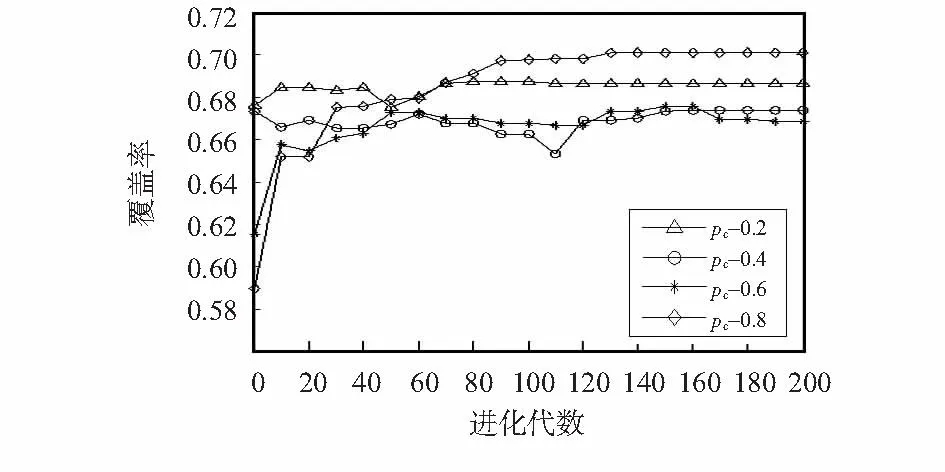
图3　覆盖率随代数的变化Fig 3　Coverage rate change with algebra

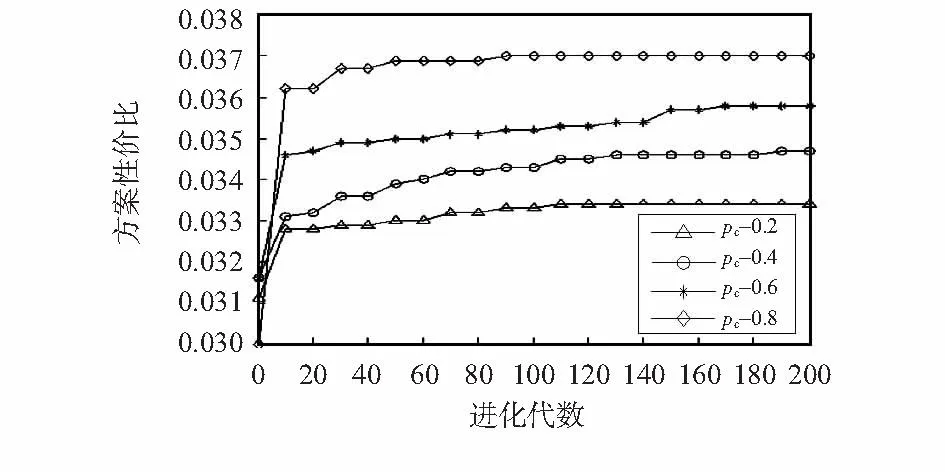
图4　方案性价比随代数的变化Fig 4　Cost performance of scheme change with algebra

3.1.2变异概率调整

为了验证变异概率的调整对算法性能的影响，此时设定交叉概率为0.8，选取变异概率分别为0.2，0.4，0.6和0.8。对算法运行20次，实验结果如图5、图6、图7所示。

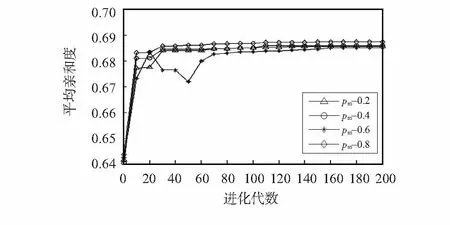
图5　平均亲和度随代数的变化Fig 5　Average affinity change with algebra

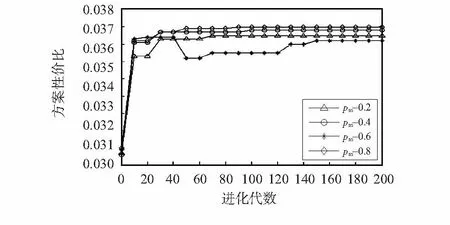
图7　方案性价比随代数的变化Fig 7　Cost performance of scheme change with algebra

图5显示了不同变异概率对算法亲和度的影响，当变异概率为0.6时，算法的平均亲和度值最高，且收敛速度最快。由图6可知，变异概率为0.6时，算法的覆盖率最高，且远高于其他情况；图7验证了不同变异概率对方案性价比的影响，可以明显看出,当变异概率为0.6时，方案的性价比值最大，表明此时算法的性能最优。

3.2对比实验

根据上述讨论，本文算法中选取交叉概率为0.8，变异概率为0.6。并与文献[3]进行了对比实验。文献[3]中选取交叉概率和变异概率均为0.6。对两种算法分别运行20次，取其平均值，对比结果如图8、图9、图10所示。

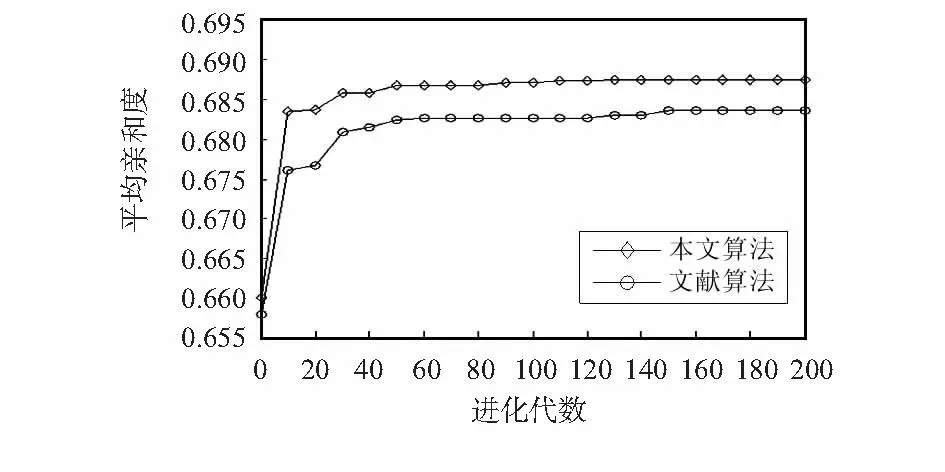
图8　平均亲和度的比较Fig 8　Comparison of average affinity

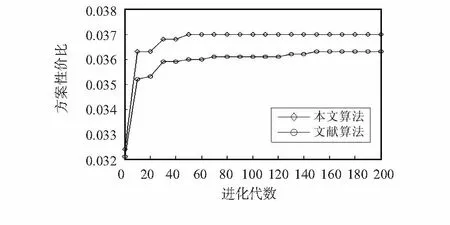
图9　方案性价比的比较Fig 9　Comparison of cost performance

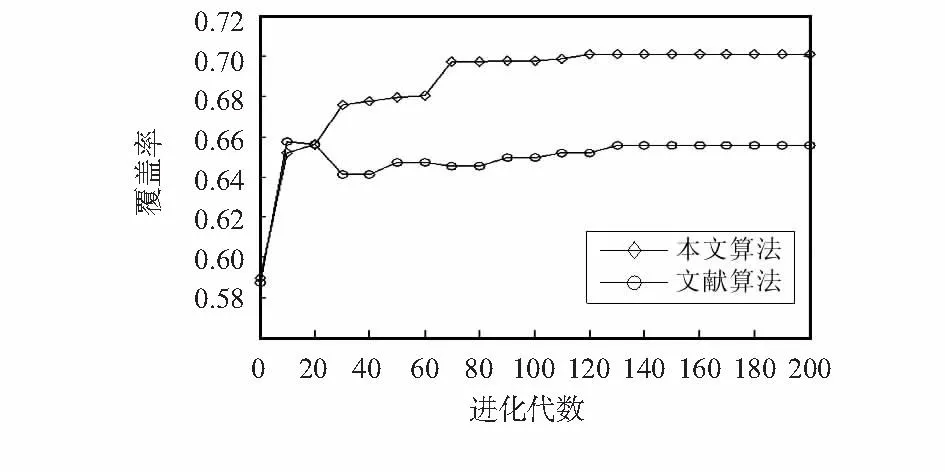
图10　覆盖率的比较Fig 10　Comparison of coverage rate

由图8可知，在进化过程中，所提算法平均亲和度曲线上升速度较快，且其值始终高于文献算法，这说明所提算法具有较好的收敛性能，且解的质量明显高于文献算法。

方案的性价比是综合评价建站成本与覆盖率的重要指标，定义为覆盖率率与建站成本的比值。由图9可知，在进化过程中，所提算法的性价比上升速度快于文献算法，且其值一直高于文献算法。这说明所提算法具有搜索能力强、收敛速度快的优点，能用相对少的基站数量满足网络的覆盖率。克隆变异算子的使用，根据抗体亲和度值和浓度值自适应地调整抗体的克隆规模，很好地保持了种群的多样性，提高了解得质量。

由图10可知，所提算法的覆盖率相比于文献算法提高了4.54 %，且收敛代数明显少于文献算法，这是因为抗体克隆规模的自适应调整，降低了算法的复杂性，提高了算法的性能。

4结束语

本文提出了一种基于矢量距的免疫算法求解基站选址优化问题，首先讨论了主要参数的变化对算法性能的影响，并与参考文献进行了对比实验。仿真结果显示，所提算法的亲和度值、覆盖率、方案性价比等性能均得到了显著的提高。另外，免疫算子的改进，增加了种群的多样性，提高了算法的收敛性能。下一步将考虑与其它智能算法相结合，同时，将地形特征等更多参数考虑到基站选址优化中，使其更贴近实际。

参考文献:

[1]Mai Wentian,Liu Hailin,Chen Lei.Multi-objective evolutionary algorithm for 4G base station planning[C]∥2013 Ninth International Conference on Computational Intelligence &Security,2013:85-89.

[2]Ali H M,Oberoi J S,Liu Jiangchuan.Base station and relay station broadband network using immune quantum evolutionary algorithm[C]∥2013 IEEE 78th Vehicular Technology Conference,2013:1-6.

[3]张英杰,毛赐平.基于免疫算法的TD-SCDMA网络基站选址优化[J].通信学报,2014,35(5):45-48.

[4]朱思峰，刘芳，柴争义.基于免疫计算的WCDMA网络基站选址优化[J].电子与信息学报，2011,33(6):1492-1495.

[5]Djalma de Melo,Carvalho Filho.Base station deployment based on artificial immune system[C]∥2008 ICCS,2008:1591-1596.

[6]石悦,邱雪松.基于免疫算法的电力通信网线路规划方法[J].北京邮电大学学报,2014,37(2):14-17.

[7]夏巧桥,田茂,汪鼎文,等.基于免疫克隆算法的认知无线电多信道联合感知方法[J].电子与信息学报,2014,36(1):55-60.

[8]朱思峰,陈国强.多目标优化量子免疫算法求解基站选址问题[J].华中科技大学学报,2012，40(1):49-52.

[9]Wang Chenshu,Chen Yidung.Base station deployment with the capacity and coverage in WCDMA systems using genetic algorithm at different height[C]∥Sixth International Conference on Genetic and Evolutionary Computing,2012:546-549.

[10] 王献荣，苏小玲.无线传感器网络中基于免疫补体优化的感知资源分配算法[J].传感器与微系统，2014,33(1):141-143.

[11] Kuang Fangjun,Jin Zhong,Xu Weihong.A novel Chaotic artificial bee colony algorithm based on tent map[C]∥2014 IEEE Congress on Evolutionary Computation(CEC),2014:235-241.

[12] Munyaneza J,Kurien A.Optimization of antenna placement in 3G network using genetic algorithm[J].The 3th International Conference on Broadband Communications &Information Technology,2009,6(2):70-80.

[13] Lu Gang,Tan Dejian,Zhao Heming.Improvement on regulating definition of antibody density of immune algorithm[C]∥Procee-dings of the 9th International Conference on Neural Information Processing,2002:2669-2672.

[14] 叶洪涛，罗飞，许玉格,等.基于新型免疫算法的污水处理过程最优控制[J].华南理工大学学报，2010，38(2):137-141.

Application of improved immune algorithm in wireless network base station location planning optimization*

MA Bao-luo1,JIA Zhen-hong1,QIN Xi-zhong1,CAO Chuan-ling2,NIU Hong-mei2

(1.School of Information Science and Engineering,Xinjiang University,Urumqi 830046,China;2.Subsidiary Company of China Mobile in Xinjiang,Urumqi 830063,China)

Abstract:In order to minimize network construction cost,improve quality of user’s service,a solution for base station location planning based on vector distance immune computation is proposed.The method for antibody concentration calculation based on vector distance is designed,a population initialization strategy based on opposition-based learning is adopted,mathematical model for problem solving is presented.The main task is to accurately determine locations and numbers of base stations,in order to reach the purpose of the minimum cost,and meet user coverage rate and system capacity.Simulation results shows that the proposed algorithm has outstanding global searching ability and fast convergence ability,can well meet user’s coverage rate needs and system capacity with low cost of station construction relatively.

Key words:wireless network;base station location planning optimization;immune optimization algorithm;opposition-based learning

DOI:10.13873/J.1000—9787(2016)05—0154—04

收稿日期：2015—08—24

*基金项目：中国移动通信集团新疆有限公司研究发展基金资助项目(XJM2013—2788)

中图分类号:TP 393

文献标识码:A

文章编号:1000—9787(2016)05—0154—04

作者简介:

马宝罗(1987-)，男，河南开封人，硕士研究生，研究方向为移动通信网络规划、无线通信。