基于矩形棱柱结构的单轴重力梯度仪设计
宋彦峥, 齐 娜, 王劲松
(中国电子科技集团公司 第四十九研究所,黑龙江 哈尔滨 150001)
基于矩形棱柱结构的单轴重力梯度仪设计
宋彦峥, 齐娜, 王劲松
(中国电子科技集团公司 第四十九研究所,黑龙江 哈尔滨 150001)
摘要:为了实现在共振的模式下进行重力梯度测量,提出一种基于矩形棱柱结构的单轴重力梯度仪。该重力梯度仪基于扭矩式测量原理,质量块采用矩形棱柱形,可减小随机噪声,提高空间分辨率。此设计结构实现了在被测方向上重力梯度值的准确测量,减少了其他方向重力场对测量的影响。给出了矩形棱柱结构重力梯度仪的系统数学模型,设计了一种单轴重力梯度仪的结构并进行了结构仿真。通过测试结果表明:该重力梯度仪实现了系统在共振的模式下进行重力梯度测量,具有结构设计简单,灵敏度高等特点。
关键词:重力梯度; 矩形棱柱; 灵敏度
0引言
重力梯度测量与重力测量相比,重力梯度测量不仅可以测量重力位的一阶导数与其分量,还可以测量重力位的二阶导数,即重力梯度张量的各个分量。根据重力梯度的异常往往能够反映出此异常体的细节,因此,综合利用各梯度张量分量信息有利于提高地质解释的准确性和描述地球动力学特性的有效性[1]。
重力梯度仪设计原理有多种,如旋转加速度计重力仪、超导重力梯度仪、静电悬浮加速度计重力梯度仪、基于扭矩测量模式重力梯度仪等。匈牙利物理学家Eotvos利用扭秤来测量水平向的重力梯度,开创了重力梯度测量的先河。后来,德国Schweydar W对Eotvos的扭秤做改进,使得重力梯度测量得到快速发展[2]。目前,重力梯度测量的重要性得到越来越广泛的认识,许多国家都投入了大量的经费进行研究,随着科学技术的发展,各种先进的重力梯度测量方法和仪器设计理念逐步应用到重力梯度系统研制中,对经济和社会的促进作用将越发明显。
1重力梯度的相关理论

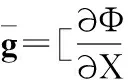
(1)
式中gx,gy,gz分别为重力在x,y,z轴上的分量。
(2)
重力梯度满足拉普拉斯方程Γxx+Γyy+Γzz=0,且重力场的旋度为零,即重力梯度张量具有对称性,因而引力梯度张量的9个分量中仅有5个是独立的,通过测量者5个重力梯度值或其线性组合即可得到全张量重力梯度值[3~5]。
2矩形棱柱结构重力梯度仪系统数学模型[6]
在有效信号振荡产生的力矩的作用下,弹性支架上质量块的运动学方程式可表示为
(3)
那么,质量块绕弹性支架偏转的角度随重力梯度的大小变化的表达式为
(4)
式中Γ为梯度张量,Ix,Iy,Iz为质量块对于相关轴的转动惯量,Ω固有振动频率、kφz为旋转钢度,ξ为摩擦系数。
当系统处于准静态方式时,转角与重力梯度关系为
(5)
当系统处于共振方式且摩擦力较小时,转角与重力梯度关系为
(6)
当系统处于临界摩擦方式时,转角与重力梯度关系为
(7)
本系统在选择在共振的模式下进行重力梯度测量,此设计方法能提高传感器的测量精度。
3重力梯度仪设计
本文设计重力梯度仪依据扭矩测量原理,通过敏感元件组件感知重力梯度信号,并将其转换为可被读取的电信号。敏感元件组件用一体化加工设计。
3.1总体结构
重力梯度仪总体结构包括敏感元件组件、力矩补偿器、角度位置传感器、敏感元件基座、下壳体、上壳体、真空阀门、高温导线、电路调理盒和电连接器。
其中,敏感元件组件为重力梯度仪的核心部件,由质量块、敏感元件机体外壳、弹性支架组成,用来感知外界重力梯度变化将其转换为可被提取的有用信号,再通过力矩补偿器、角度位置传感器将重力梯度信号转换为可识别的电流值。重力梯度仪总体结构如图1所示。
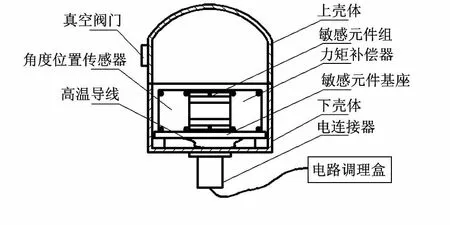
图1 重力梯度仪总体结构Fig 1 Overall structure of gravity gradiometer
3.2敏感元件组件结构设计
重力梯度仪敏感元件组件的质量块与敏感元件机体外壳在安装在同一平面上。基于敏感元件组件安装工艺的要求,将质量块与弹性支架质量块加工为一体,如图2所示。两个弹性支架位于质量块两侧和敏感元件机体外壳连接在一起,质量块、敏感元件机体外壳、弹性支架共同组成敏感元件组件。弹性支架中心线与质量块转轴的中心线为同心结构,以弹性支架为轴,质量块做微角度旋转。
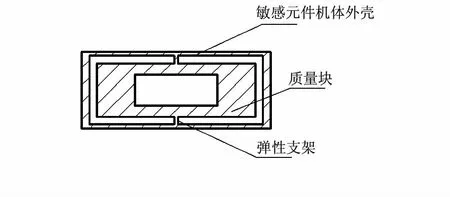
图2 敏感元件组件结构设计Fig 2 Design of sensitive element subassembly
质量块为矩形棱柱形,敏感元件机体外壳与质量块形状相同,质量块位于敏感元件机体外壳内部,且质量块与敏感元件机体外壳位于同一平面内,两个弹性支架分别固定于质量块的顶部和底部,两个弹性支架均与敏感元件机体外壳固定连接在一起,质量块能够以弹性支架为轴做微角度旋动。这样,就构成了稳定的机械耦合系统,在保证测量轴稳定性的同时,限制了其他自由度方向对测量结果的影响。
3.3质量块设计
质量块为矩形棱柱的形状,在重力场的作用下,由质量块振动方式可知,Iy-Ix值越大,则角φ摆动幅值越大。转动惯量I的值由质量块的外形尺寸和材质决定,质量块为棱柱形,延x,y,z轴的三个尺寸分别用L,w,h表示。内部切口尺寸为L1,w,h1表示,如图3所示。质量块的转动惯量计算表达式为
(8)

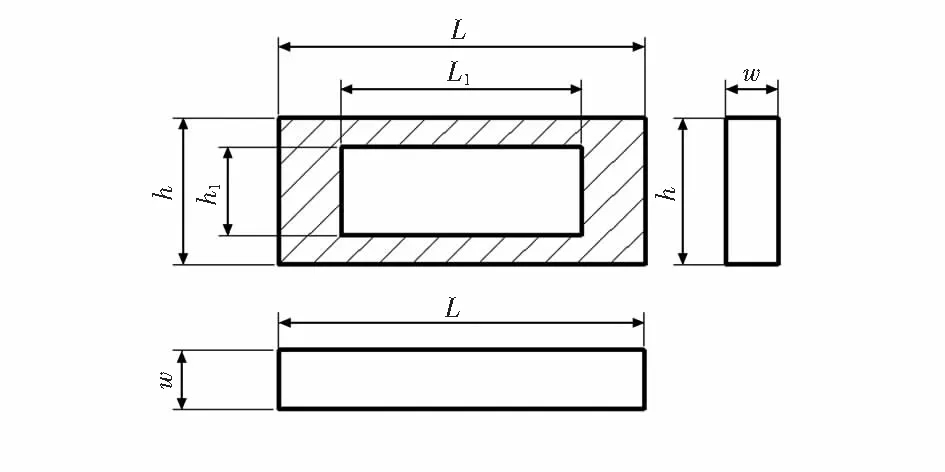
图3 质量块外形尺寸图Fig 3 Dimension diagram of mass block
3.4弹性支架设计
两个弹性支架为圆柱体分别固定于质量块的顶部和底部,两个弹性支架中心线与质量块竖直方向的中心线重合,且两个弹性支架均与敏感元件机体外壳固定连接在一起,质量块能够以弹性支架为轴做微角度旋转。

图4 弹性支架剖面图Fig 4 Profile map of elastic support
4信号调理
设计中,将重力梯度仪的敏感元件组置于电场E内,在电场的作用下使得质量块的振动频率达到系统的固有频率,则系统达到共振。根据式(9)可得出在重力梯度场Γ下的电流值[8]

(9)
如图5和图6所示,可得出与当质量块在共振的模式下电场所得出的电流随时间变化曲线偏转角随时间变化曲线一致。

图5 偏转角随时间变化的曲线关系图Fig 5 Curve diagram of deflection angle varies with time

图6 电流随时间变化的曲线关系图Fig 6 Curve diagram of current changes with time
通过式(10)可以计算本系统的设备灵敏度,单位用安培/厄缶来表达,公式如下
(10)
5设计仿真
分别将敏感元件组分别沿X,Y,Z轴3个方向的摆动以及围绕X,Y,Z轴3个方向的摆动用软件模拟出来,分析对比模拟结果,如图7、图8所示。

图7 敏感元件沿轴的固有摆动Fig 7 Inherent oscillation of sensitive element along shaft

图8 敏感元件围绕轴的固有摆动Fig 8 Inherent oscillation of sensitive element around shaft
经过对比分析得出:质量块的惰性振动的固有频率明显区别于围绕敏感轴摆动的固有频率,且工作状态下,施加电流激励时两者的差别更为明显。这样,就可以最大限度地配布测量轴和惰性自由级的频率,以敏感元件模块数值模拟来确定任何自由级质量块摆动的固有频率并优化弹性元件结构,提高模块的测量性能。
5结论
本文基于矩形棱柱结构设计重力梯度仪的敏感元件组件,通过力矩补偿器和角度传感器将重力梯度信号转换为电信号,并通过电路调理盒将信号以电流的形式输出,经研究表明,系统可以在共振的模式下进行重力梯度测量。仿真结果表明:该重力梯度仪具有结构设计简单,灵敏度高、抗干扰能力强等特点。
参考文献:
[1]彭益武,赵立珍,屈少波,等.二维簧片重力梯度仪的研制[J].物探与化探,2006,30(5):401-409.
[2]吴琼,腾云田,张兵,等.世界重力梯度仪的研究现状[J].物探与化探,2013,37(5):761-768.
[3]李纪莲,罗诗途.航空重力梯度仪研究现状[J].传感器与仪器仪表,2008,24(5-1):121-123.
[4]赵立珍,彭益武,周泽兵.基于扭矩测量的二维簧片重力梯度仪的设计[J].大地与地球动力学,2006,26(2):128-133.
[5]张昌达.航空重力测量和航空重力梯度测量问题[J].工程地球物理学报,2005,2(4):282-290.
[6]穆迪M V.带有扭转挠曲枢轴的重力梯度仪:中国,200980147536.3[P].2016-10-26.
Design of monaxial gravity gradiometer based on configuration of rectangle prism
SONG Yan-zheng, QI Na, WANG Jin-song
(49th Research Institute,China Electronics Technology Group Corporation,Harbin 150001,China)
Abstract:A monaxial gravity gradiometer based on configuration of rectangle prism is proposed in order to realize gravity gradient measurement in resonance mode.The gravity gradiometer is based on principle of torsion measurement,mass block use configuration of rectangle prism,it can reduce random noise and enhance spatial resolution.The design configuration realizes accurate measurement of gravity gradient,reduce influence of gravity field in other directions on measurement,give mathematical model for structure of rectangular prism gradiometer,structure of monaxial gradiometer is simulated. The simulation results show that the gravity gradiometer realize gravity gradient measurement in resonance mode,it has the characteristics of simple structure, high sensitivity.
Key words:gravity gradient; rectangle prism; sensitivity
DOI:10.13873/J.1000—9787(2016)04—0073—03
收稿日期:2016—02—24
中图分类号:TP 273
文献标识码:A
文章编号:1000—9787(2016)04—0073—03
作者简介:
宋彦峥(1969-),男,黑龙江哈尔滨人,研究员,主要研究方向为传感器与测量技术。

