高速公路通道路网交通诱导决策模型

王晓飞　李新伟,2　刘立能　杜锦涛

(1华南理工大学土木与交通学院， 广州 510641)(2广州市高速公路有限公司， 广州 510288)

高速公路通道路网交通诱导决策模型

王晓飞1李新伟1,2刘立能1杜锦涛1

(1华南理工大学土木与交通学院， 广州 510641)(2广州市高速公路有限公司， 广州 510288)

摘要:为解决灾变事件发生时一条最优路径和多条可绕行路径的决策问题，应用图论及最优化理论相关方法构建模型.以通道路网为研究对象、实时安全可靠度为基本约束条件，采用图论相关方法研究了诱导起终点间通路求解方法.应用最优化理论建立运营安全最优路径决策模型，并采用Dijkstra算法求解最优路径.在解决最优路径的基础上，引入重复度的概念及相应算法，研究其他可绕行路径的决策模型.针对高速公路通道路网，构建了灾变事件下的交通诱导决策模型，解决综合考虑安全、行程时间和通行需求的路径决策.结果表明，图论方法能求解任意起终点间的所有通路，Dijkstra算法能求解最优路径，应用重复度算法可寻求其他可绕行路径以满足灾变事件下的绕行需求.

关键词:高速公路；通道路网；运营安全；行程时间；路径决策

经过30多年的发展，我国公路路网基本形成，很多省份的公路网整体功能和技术水平已接近发达国家，但与此不匹配的道路管理水平尚不能自如地应对灾变事件.2008年春运期间，我国发生了严重的雪灾，在较大范围内造成交通拥堵以及一系列损失惨重的交通事故，由于没有完善的管理对策，部分高速公路只能采取关闭措施[1].为了有效利用现有公路网资源、保障高速公路的运营安全及充分发挥现有公路设施整体效能，需要适时、超前地研究基于路网的运营安全管理问题.

交通诱导系统是智能交通系统的重要子系统之一[2].诱导系统的核心理论是建立科学有效的诱导决策模型.目前，相关学者在动态路径诱导方面研究较多，但绝大多数都只给出了一条最优路径[3-7]，单条最优路径模型能满足非灾变条件下道路用户的要求.但对于道路管理者而言，发生灾变事件时，需要为事件影响范围内的交通流制定管理对策，提供足够多的疏散路径.因此，研究通道路网的多条疏散路径确定方法已成为该领域的发展趋势.此外，绝大多数的研究关注于行程时间最优，将实时运营安全作为最优化模型或基本约束条件的相关文献则较少.

基于此，本文以灾变事件下高速公路所处的局域路网为对象，从通道路网角度出发，以运营安全为基本约束条件，行车时间最短为决策依据，进行多条疏散路径决策研究，以满足安全通行要求，真正发挥路网的整体效率.

1建模基础

1.1通道路网

本文研究的通道路网由高速公路主线、邻近若干并行的其他等级道路以及相互间的连接线组成．路网中某高速公路并行线主要为路段范围内事件处理的绕行路线,作为并行线的其他等级道路应具有一定的通行能力和服务水平,并且与该高速公路相距不能太远．绕行线路不能随意确定,应根据一定的指标进行择优选用．采用关联度的方法,对高速公路的邻近道路进行关联度评价,然后根据关联度大小排序,将关联度较大的道路作为该高速公路的并行辅助线[8]．

随着路网的确定,路网节点也随之确定．其中,路网节点包括内部高速公路之间的交点及起终点．

1.2管理单元的划分

管理单元是进行公路管理的基本分析单元．管理单元的划分因系统目标而异,明确系统目标是管理单元划分的前提[9]．本文基于高速公路通道决策模型而展开研究．划分管理单元时,首先确定路网中不同等级、道路设施条件、路名的路线,然后,将上、下行公路分开考虑,以若干具有代表性的构造物作为划分管理单元的重要节点(如起终点、立交、收费站、带回转车道的隧道起终点、出入口等),从而得到各类管理单元．

1.3实时安全可靠度的确定

实时安全可靠度可定义为一定的交通、气候和道路环境下车辆能够保持安全运行的概率[1]．本文采用多个指标表征管理单元i于t时刻的实时安全可靠度S(i,t),由结构函数的期望值给出[10],即

S(i,t)=wsSS(i,t)+wDSD(i,t)

(1)

式中,SS(i,t)为管理单元i在t时刻的静态安全可靠度,可由文献[10]计算得到;ws为静态安全可靠度的权重,wD为动态安全可靠度的权重,ws+wD=1;SD(i,t)为管理单元i在t时刻的动态安全可靠度,且

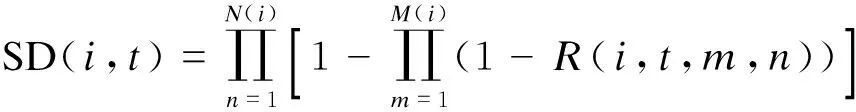
式中,N(i)为管理单元i的车辆检测器布设的断面数量;M(i)为管理单元i的车道数;R(i,t,m,n)为管理单元i中第m个车道上第n个车辆检测器处t时刻的实时安全可靠度,且

式中,φ(i,t)为管理单元i在t时刻的路面附着系数,干燥气候下水泥混凝土路面可取0.7,沥青混凝土路面可取0.6;g为重力加速度;a(i,t,m,n)为管理单元i中第m个车道上第n个车辆检测器处t时刻的安全制动减速度,且[10]

式中,V(i,t,m,n), H(i,t,m,n)分别为管理单元i在车道m处布设的第n个车辆检测器于t时刻的行驶速度和至车头的间距;ac为紧急制动减速度,根据紧急情况,一般取-3～-6m/s2; T(i,t)为t时刻管理单元i的驾驶员反应时间,一般取3s;Lsafe为车辆的安全距离．

1.4诱导范围的确定

诱导范围的确定是制定通道路网管理的基础．当事件发生时,交通诱导应为事件影响范围内的车辆提供足够数量的可绕行路线．目前的技术还难以实现对单个驾驶员的动态诱导,仅能通过布设于沿线的信息板发布诱导信息,可发布的信息量有限,无法实现任意2点间最优路径的完整发布．为此,本文将诱导起终点分为两大类:① 静态起终点,即任何环境下的主要起终点,这些节点包括高速公路的起终点、高速公路途径的重要城市、大交通量的出入口等;② 动态起终点,即灾变条件下为使车辆避开事发单元及受事件影响路段的起终点．诱导起点的确定应考虑事件影响范围和事发点与诱导起点间的交通疏导要求2个因素．诱导终点(迂回点)可直接选取离事发单元下游最近的出入口．

2通道路径诱导决策模型

本文中的路径诱导步骤如下:

① 基于OD集合中任意2点间通路求解模型;

② 以运营安全为首要约束条件,研究基于运营安全的最优路径决策模型;

③ 以通行疏散需要为前提条件,研究k条绕行路径的决策模型．

2.1两点通路求解算法

图1　带回路的通路

流体网络理论中,任意节点vr到vs的全部通路数为[11]

(2)

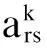
所有节点之间的全部通路求和是路网诱导系统研究中的重点,其计算公式为

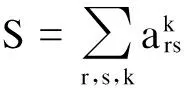
(3)

式中,V-(G)为出发点集合;V+(G)为到达点集合．通过矩阵运算直到Ak=0．

代入各弧元素e,构建成矩阵Ae,令U=Ae+I．取行列式中usr对应的余子式便可得到vr和vs之间的所有通路．

2.2基于运营安全的最优路径决策模型

在任意两点o,d间,寻找满足实时安全可靠度要求的最优路径数学表达式为

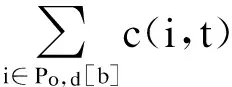
s.t.S(i,t)≥Sc

(4)

式中,c(i,t),S(i,t)分别为管理单元i在t时刻所需的行程时间和安全可靠度;Po,d为o,d间的所有通路集合;Po,d[b]为o,d间的第b条通路;Sc为临界安全可靠度．

2.2.1路阻函数

考虑以道路运营安全作为基本约束条件,对路阻函数进行如下修正:

(5)

式中,C(i,t),K(i,t)分别为管理单元i在t时刻的行程时间和车流密度;Li为管理单元i的长度;Kjam为阻塞密度;vf为自由流车速．

当主线高速发生交通事故时,车辆行程时间的计算分为2种情形:交通事故未消散和交通事故已消散．取两者中的较大值进行计算,则C(i,t)为

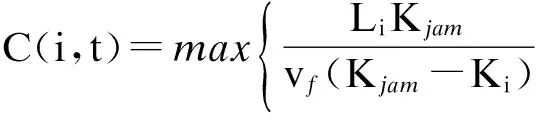
(6)

式中,Ki为管理单元i的车流密度;Kr为管理单元i的上游车流密度;L2为事发点与管理单元i终点之间的距离;te为事件清除时间;t0为事件发生时间．

2.2.2最优路径

未发生交通事件时,可直接应用Dijkstra算法进行搜索,计算流程参见文献[12]．

当高速公路发生交通事件时,车辆继续在高速上行车的行程时间按式(6)计算,其他绕行路径中最优路径的行车路线和行程时间可由最优搜索算法求得．其步骤如下:

① 应用Dijkstra算法搜索绕行路线中的最优路径,将最优路径行程时间记为TR．

② 选择在主线高速公路继续行驶,按照式(6)计算所需行程时间TF．

③ 搜索最优路径．取TPo,d[1]=min{TR,TF}和TPo,d[1]=min{TR,TF}中较小者对应的通路为最优路径,记为Po,d[1],即TPo,d[1]=min{TR,TF}.

2.3其他绕行路径决策模型

本文采用重复度R为决策变量．重复度的定义为,该路径与已选出的绕行路径共有路段的总长度与本身的总长度之比[11],其计算公式如下:

(7)

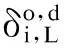
在已搜索到的最优路径的基础上,继续搜索第b条可绕行路径的决策模型表达式为

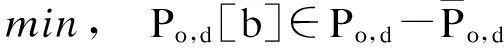
s.t.S(i,t)≥Sc,TPo,d[b]≤Tod,c

(8)

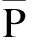
由此可知, 在已搜索到的最优路径基础上,若要继续辨识出其他b条点o至点d的绕行路径,需经过b次循环计算,具体步骤如下:

① 初始化b=1;

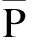
④ 采用通路法计算第b+1条路径容量,如能满足需求,则转向第⑦步,否则转向第⑤步;

⑥ 令b=b+1,返回第②步;

3实例

图2为某高速通道路网,其中v0→v1→v2→v3→v4为主线高速公路,双向六车道．假定一级路肩交通事故的清除时间为10 min;二级交通事故占用1个车道,事件清除时间为20 min;三级交通事故占用2个车道,事件清除时间为30 min;四级重大事故需封闭交通40 min．要求管理单元的实时安全可靠度不小于0.6．根据该项目背景,得到如表1所示的各管理单元数据．

图2　计算实例

道路管理单元平均速度/(km·h-1)车流量/(pcu·h-1)通行能力/(pcu·h-1)主线高速10036286750四车道高速11211204500二级公路803201200

各级事件下管理单元e4的实时安全可靠度可根据式(1)计算得到，计算过程中，wD、ws、附着系数、驾驶员反应时间等参数按文献[1]选取.不同等级事故条件下实时安全可靠度S(i,t)见表2.

表2　各级交通事件下实时安全可靠度

当管理单元e4发生一级事件时,主线高速公路通行能力满足要求,实时安全可靠度0.75满足安全通行要求,无需进行交通诱导．

当管理单元e4发生二级事件时,实时安全可靠度满足安全通行要求．根据文献[12],通行能力降低为原来的49%,按每车道基本通行能力2 200 pcu/h计算,剩余通行能力为2 200×3×0.49=3 234 pcu/h,不满足当前通行需求(3 628 pch/h)．根据通行需求、事件影响范围及路网结构,诱导范围确定为v2→v3→v4．根据2.2节中的模型,搜索到第1条可绕行路径P3,4[1]={e3,e11,e6,e13}．

对搜索到的路径需进行通行能力检验, 在节点v2→v4之间搜索到2条路径,即继续行走高速公路的路径P3,4[0]={e3,e4}和可绕行路径P3,4[1]={e3,e11,e6,e13},其通行能力为4 508 pcu/h,满足通行需求(3 948 pcu/h),故不需再搜索其他绕行路径．

当管理单元e4发生三级事件时,不满足实时安全可靠度和通行需求．诱导范围定为v2→v3→v4．根据文献[12],通行能力降低为原来的17%,剩余通行能力为2 200×3×0.17=1 122 pcu/h．根据2.2节中的模型,搜索最短路径可得P3,4[1]={e3,e11,e6,e13}．

进一步进行通行能力检验,在节点v2→v4中搜索到2条路径P3,4[1]={e3,e11,e6,e13}和P3,4[0]={e3,e4},其通行能力取瓶颈较小值2 348 pcu/h,不满足通行需求(3 948 pcu/h)．根据2.3节中的模型,需寻找其他绕行路径,具体步骤如下:

① 根据2.1节中的模型确定v2→v3→v4中的其他通路为P3,4[2]={e21,e17,e23},P3,4[3]={e3,e22,e19,e24,e23},P3,4[4]={e3,e11,e12,e8,e14,e13}．

② 按照式(7),计算各路径的重复度,得到RP2,4[2]=0,RP2,4[3]=0.25,RP2,4[4]=0.33．取重复度较小的路径P2,4[2]作为第2条绕行路径．

③ 检验通行需求是否满足要求．此处,P2,4[0],P2,4[1],P2,4[2]的通行能力之和为6 848 pcu/h,满足通行需求之和5 068 pcu/h．

当管理单元e4发生四级事件时,计算方法类似,可获得路径P2,4[0],P2,4[1],P2,4[2]．

4结语

路径决策模型是交通诱导系统中的关键决策模型．本文以高速公路主线通道路网为研究对象,构建了基于运营安全的路径决策模型,以解决灾变事件发生时一条最优路径和多条可绕行路径的决策问题．本文提出的决策模型充分考虑了诱导路径的实时安全可靠度、行程时间和通行能力,并解决了诱导起终点间可能通路的求解方法．该模型能为可变信息板为主的交通诱导方式提供决策依据．

本研究以通道路网为对象,决策方法适用于以高速公路为主线的小型局域路网．研究成果应用于大型区域路网时,需进一步开发完整可靠的应用系统,并提出相应算法．

参考文献(References)

[1]王晓飞. 灾变条件下通道路网运营安全管理及应急处置研究[D]. 上海:同济大学交通运输工程学院,2008.

[2]谢秋燕. 车联网条件下车辆动态路径诱导方法研究[R].广州:华南理工大学土木与交通学院, 2012.

[3]龙琼, 曾革, 张谨帆, 等. 面向驾驶员个性化需求的动态路径诱导方法[J]. 中南大学学报(自然科学版), 2013, 44(5):2124-2129.

Long Qiong, Zeng Ge, Zhang Jinfan, et al. Dynamic route guidance method facing driver’s individual demand[J].JournalofCentralSouthUniversity(ScienceandTechnology), 2013, 44(5):2124-2129. (in Chinese)

[4]杨群, 关伟, 张国伍. 基于合理多路径的路径选择方法的研究[J]. 管理工程学报, 2002, 16(4):42-45.DOI:10.3969/j.issn.1004-6062.2002.04.010.

Yang Qun, Guan Wei, Zhang Guowu. Study on multi-path based route choice approach[J].JournalofIndustrialEngineeringandEngineeringManagement, 2002,16(4):42-45.DOI:10.3969/j.issn.1004-6062.2002.04.010. (in Chinese)

[5]Lee C K. A multiple-path routing strategy for vehicle route guidance systems[J].TransportationResearchPartCEmergingTechnologies, 1994, 2(3):185-195.

[6]Yang Q, Zhao Y. A fuzzy logic-based frame work for route choice in vehicle navigation systems[J].JournalofSystemsScienceandSystemsEngineering, 2000, 9(4): 467-474.

[7]杨兆升, 初连禹. 动态路径诱导系统的研究进展[J]. 公路交通科技, 2000, 17(1): 34-38. DOI:10.3969/j.issn.1002-0268.2000.01.010.

Yang Zhaosheng, Chu Lianyu. Study on the development of the dynamic route guidance systems (DRGS)[J].JournalofHighwayandTransportationResearchandDevelopment, 2000, 17(1): 34-38.DOI:10.3969/j.issn.1002-0268.2000.01.010. (in Chinese)

[8]王晓飞, 柳本民, 郭忠印.并列型高速公路安全管理路网构建[C]//第七届世界华人交通运输学术会议论文集.北京:人民交通出版社,2007:8-12.

[9]邵敏华, 孙立军. 公路管理单元动态划分技术与数据模型研究[J]. 同济大学学报(自然科学版), 2004, 32(3):343-347.

Shao Minhua, Sun Lijun. Research on segmentation technique and data modeling in highway management system[J].JournalofTongjiUniversity(NaturalScience), 2004, 32(3):343-347. (in Chinese)

[10]王晓飞, 郭忠印. 高速公路网管理单元的实时安全可靠度[J]. 华南理工大学学报(自然科学版), 2009, 37(7):15-20.Wang Xiaofei, Guo Zhongyin. Real-time safety reliability of management unit of freeway network[J].JournalofSouthChinaUniversityofTechnology(NaturalScienceEdition), 2009, 37(7):15-20. (in Chinese)

[11]卢开澄, 卢华明. 图论及其应用[M]. 北京:清华大学出版社, 1995:37-49.

[12]美国交通研究委员会TRB. 道路通行能力手册(精)[M]. 任福田,等译. 北京:人民交通出版社, 2007:236-239.

Trafficrouteguidancedecision-makingmodelforfreewaycorridor

WangXiaofei1LiXinwei1,2LiuLineng1DuJintao1

(1SchoolofCivilEngineeringandTransportation,SouthChinaUniversityofTechnology,Guangzhou510641,China) (2GuangzhouExpresswayCo.,Ltd.,Guangzhou510288,China)

Abstract:To decide an optimal route and several alternate routes under disastrous conditions, a guidance decision-making model is proposed based on the graph theory and the optimization theory. Taking freeway corridor as the research object and real-time safety reliability as the basic constraint condition, the solution method for connected routes between the initial point and the ending point is studied by using the graph theory. The optimal route decision-making model based on safety is built by the optimization theory and the optimized route is solved by the Dijkstra algorithm. On the basis of the optimized route, the conception of multiplicity and the corresponding algorithm are introduced to study the models of other alternate routes. Aimed at the freeway corridor, the traffic route guidance decision-making model under disastrous conditions is proposed to solve the route decision taking safety, travel time，and traffic demand into consideration comprehensively. The results show that all connected routes between the initial point and the ending point can be solved by the graph arithmetic and the optimized route can be solved by the Dijkstra algorithm. Furthermore, other alternative routes can be solved by the multiplicity algorithm to satisfy route requirements under disastrous conditions.

Key words:freeway; corridor; operation safety; travel time; route decision

doi:10.3969/j.issn.1001-0505.2016.03.031

收稿日期:2015-06-01.

作者简介:王晓飞(1980—)，女，博士，讲师，xiaofeiw@scut.edu.cn.

基金项目:国家自然科学基金资助项目(51278202，51408229)、广东省交通运输厅科技资助项目(2013-02-068，2015-02-003， 2015-02-004).

中图分类号:U491

文献标志码:A

文章编号:1001-0505(2016)03-0641-05

引用本文:王晓飞,李新伟,刘立能,等.高速公路通道路网交通诱导决策模型[J].东南大学学报(自然科学版),2016,46(3):641-645.DOI:10.3969/j.issn.1001-0505.2016.03.031.