考虑超固结比影响的硬黏土应力灵敏度变化规律

卞　夏　 丁建文　 史　剑

(1河海大学岩土力学与堤坝工程教育部重点实验室, 南京 210098)(2河海大学岩土工程科学研究所, 南京 210098)(3东南大学岩土工程研究所, 南京 210096)

考虑超固结比影响的硬黏土应力灵敏度变化规律

卞夏1,2丁建文3史剑3

(1河海大学岩土力学与堤坝工程教育部重点实验室, 南京 210098)(2河海大学岩土工程科学研究所, 南京 210098)(3东南大学岩土工程研究所, 南京 210096)

摘要:为了分析土结构性对强超固结性硬黏土力学性状的影响,提出了考虑超固结比影响的固有压缩线的概念,重新定义了考虑超固结比影响的硬黏土应力灵敏度．通过耦合超固结比和土结构性对硬黏土力学性状的影响,并将应力灵敏度的概念从单一应力水平拓展至当前应力水平,探讨了考虑超固结比影响的硬黏土应力灵敏度随应力水平的变化规律．结果表明:在半对数坐标系中,考虑超固结比影响的硬黏土应力灵敏度与重塑孔隙指数呈线性关系．不同硬黏土应力灵敏度随应力水平的变化规律能够通过孔隙指数差进行归一化处理．基于考虑超固结比影响的硬黏土应力灵敏度变化规律,提出了屈服后阶段硬黏土压缩曲线的计算模型．

关键词:硬黏土;土结构性;应力灵敏度;超固结比

随着地面空间利用率的逐渐饱和,地下空间的开发利用变得越来越重要．例如,英国伦敦地铁系统已经延伸至地下近百米[1];核废料往往需要放置在地下几百米深处进行处置[2]．地下较深处所要面对的研究对象往往是硬黏土．Cui等[2]着重研究了硬黏土作为核废料处置中的载体,在热-水-力耦合作用下的力学性质问题;郭杨等[3]分析了硬黏土中PHC管桩中的承载力问题;周健等[4]探讨了地铁动荷载作用下硬黏土的力学特性．

天然沉积硬黏土在沉积过程和后沉积过程中受到风化、侵蚀等作用,具有很强的超固结性,一般采用超固结比(即历史上受到的最大有效应力与当前有效应力的比值)进行定量描述．硬黏土的压缩、强度等力学性状均受超固结比影响,与软黏土存在较大差异[5-8]．近期研究表明,天然沉积硬黏土同样受到土结构性的影响,使得在相同孔隙比下天然沉积硬黏土相比于重塑土能够承受更大的压力,具有更大的峰值强度和体积模量[8-9]．因此,研究硬黏土力学性状时需要着重探讨超固结比和土结构性的影响．目前,在定量评价土结构性对天然沉积土力学性状影响的研究中,最为重要的成果为Chandler等[7,10]提出的灵敏度评价体系．该体系中的评价基准线——固有压缩线ICL的应力灵敏度为1．然而,天然沉积硬黏土通常具有强超固结性,两者之间初始状态的不一致性会导致无法直接定量评价土结构性对天然沉积硬黏土力学性状的影响．因此,如何耦合考虑超固结性和土结构性对于天然沉积硬黏土力学性状的影响,以及如何定量评价土结构性对天然沉积硬黏土力学性状的影响,是值得进一步深入研究的课题．

本文通过收集已有文献中的天然沉积硬黏土压缩曲线,考虑超固结比的影响,拓展了硬黏土应力灵敏度的概念,并以此为基础探讨了硬黏土应力灵敏度随应力水平的变化规律．

1应力灵敏度

Burland[6]提出的孔隙指数定义如下:

(1)

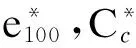
(2)

(3)

式中,eL为液限孔隙比．式(2)和(3)适用于液限范围为25%～160%的土样．

Burland[6]指出,初始含水率为1.25倍液限重塑土的压缩曲线能够归一化为唯一的固有压缩线ICL,表示为

(4)

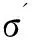
基于Burland[6]提出的固有压缩概念,Chandler等[7,10]以应力灵敏度作为定量描述天然沉积土与重塑土力学性状差异的唯一变量,提出了灵敏度评价体系,为定量评价土结构性对天然沉积土力学性状的影响提供了基础理论体系．Gasparre等[9]扩展了应力灵敏度的概念,将单一应力水平拓展至当前应力水平,假定应力灵敏度Sσ表示当前应力水平下天然沉积硬黏土压缩曲线与ICL上相同孔隙指数对应竖向有效应力的比值,即

(5)

为了研究硬黏土应力灵敏度随应力水平的变化规律,本文收集了已有文献中12组典型的硬黏土一维压缩试验数据进行分析．硬黏土的基本物性指标列于表1．由表可知,硬黏土的天然含水率与液限的比值为0.35～0.50,远低于液限含水率．硬黏土的超固结比为2.4～17.0,大部分硬黏土具有强超固结性．

采用Burland[6]提出的固有压缩参数经验公式得到的硬黏土归一化压缩曲线绘于图 1中．图中,Iv为硬黏土孔隙指数．由图可知,以Burland[6]提出的固有压缩参数经验公式计算孔隙指数,将硬黏土压缩曲线进行归一化后,常会出现归一化压缩曲线位于固有压缩线ICL下方的现象,即应力灵敏度小于1,显然与灵敏度评价理论体系矛盾．这表明应用灵敏度评价体系分析土结构性对硬黏土力学性状影响时,受超固结比影响的天然沉积硬黏土压缩曲线与固有压缩线ICL间初始状态不一致的现象将导致分析结果不合理．

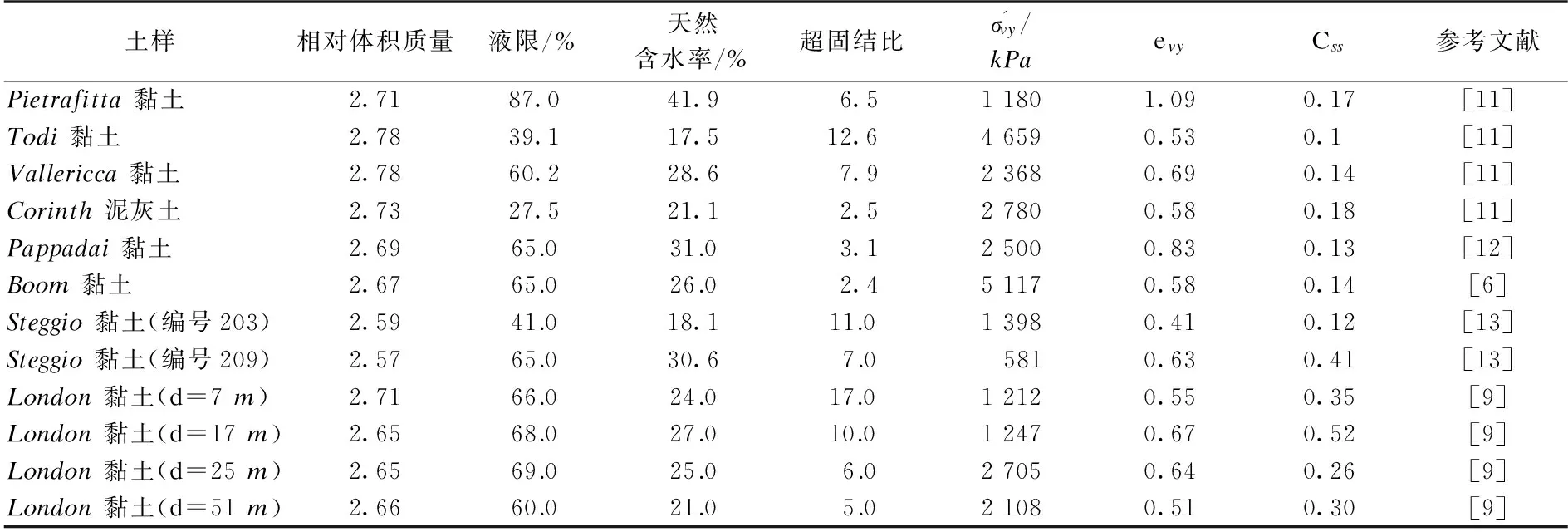
表1　12组硬黏土基本物性指标

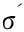
图1　归一化硬黏土压缩曲线

2考虑超固结比的应力灵敏度定义

灵敏度评价体系的评价基准固有压缩线ICL是基于正常固结重塑土压缩试验得到的,其对应的超固结比为1,而天然沉降硬黏土具有强超固结性,因此,对天然沉积硬黏土进行灵敏度评价时需要对评价基准线——固有压缩线ICL进行拓展．如图 2所示,通过将固有压缩线ICL沿横坐标向左平移可使平移后的拓展固有压缩线与天然沉积硬黏土压缩曲线具有相同的超固结比,从而耦合考虑了超固结比和土结构性对硬黏土压缩性状的影响．

因此,考虑超固结比影响的硬黏土应力灵敏度可表示为

(6)

式中,ROCR为超固结比．

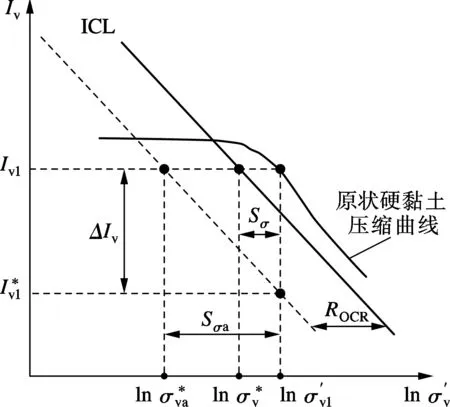
图2　考虑超固结比的硬黏土应力灵敏度定义

3硬黏土应力灵敏度的变化规律

3.1硬黏土应力灵敏度与重塑孔隙指数的关系

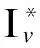
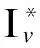
(7)

式中,bss为线性关系的截距,与土体特性相关．

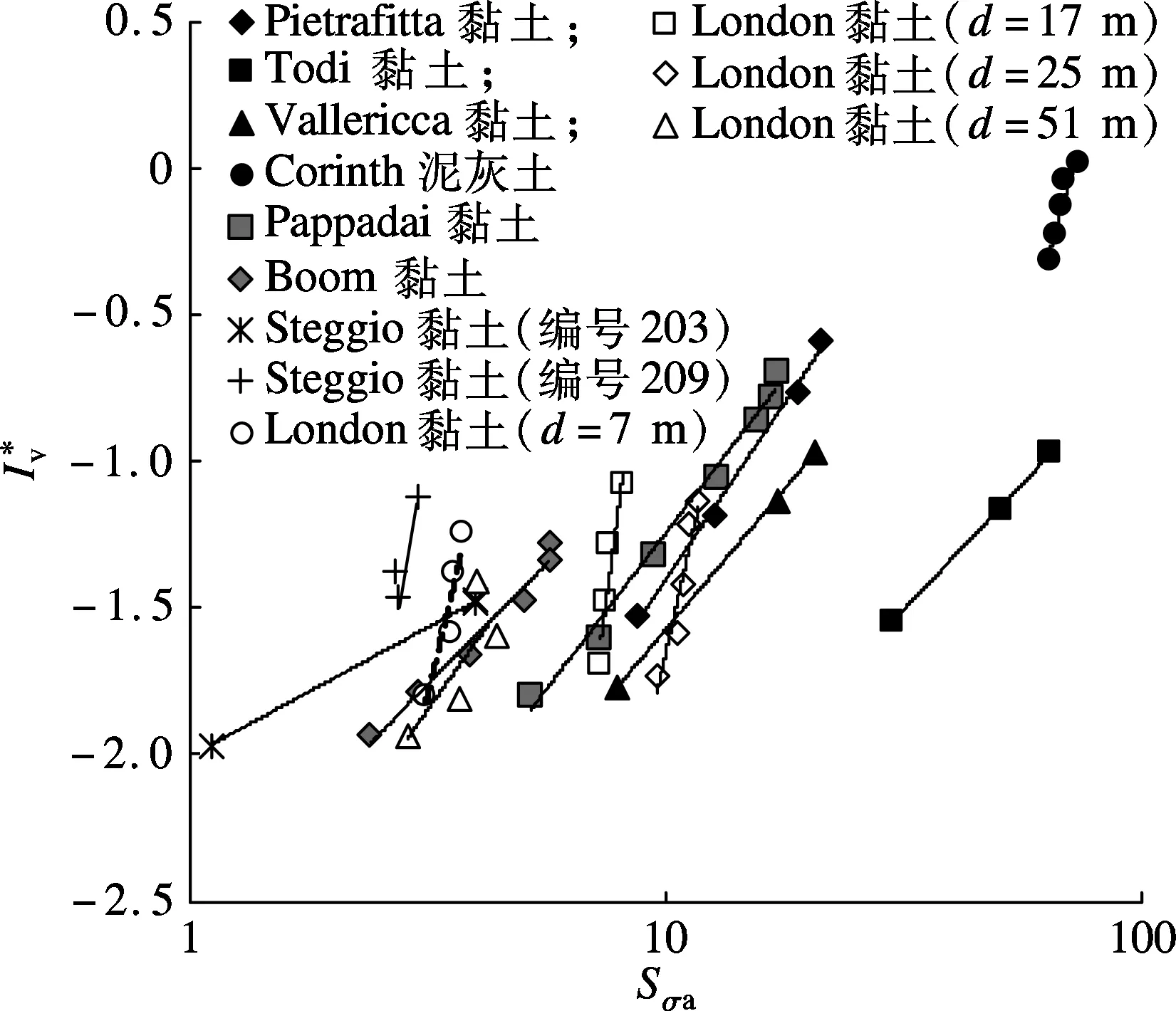
图3　硬黏土应力灵敏度与重塑孔隙指数的关系

3.2硬黏土应力灵敏度与孔隙指数差的关系

受土结构性影响,在相同固结压力下天然沉积硬黏土压缩曲线与固有压缩线ICL存在孔隙指数差ΔIv(见图2)．考虑超固结比影响的硬黏土应力灵敏度Sσa与对应孔隙指数差ΔIv的变化关系见图 4．由图可知,在半对数坐标系中,Sσa与ΔIv呈现良好的线性关系,可以表示为

ΔIv=0.25lnSσa

(8)

由式(8)可知,应力灵敏度Sσa越大,所对应的孔隙指数差ΔIv也越大,表明土结构性越强,所能抵抗的孔隙指数差越大．随着应力水平的增大,土结构性逐渐损伤,应力灵敏度Sσa伴随着孔隙指数差ΔIv逐渐减小．当Sσa=1时,ΔIv=0,土结构性完全丧失,天然沉积硬黏土压缩曲线回到固有压缩线ICL上．因此,不同天然沉积硬黏土的应力灵敏度随应力水平的变化规律可以采用孔隙指数差ΔIv进行归一化．

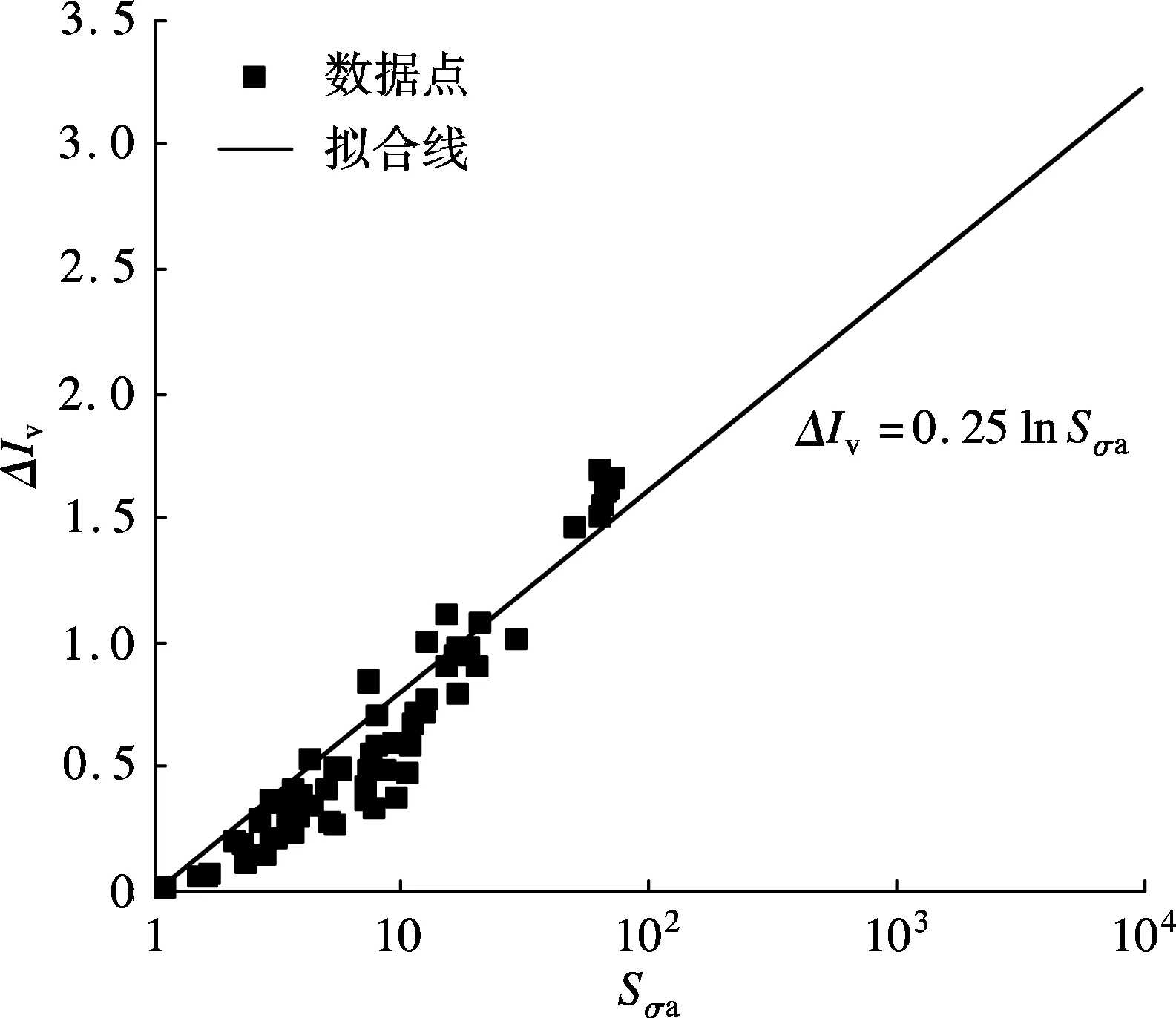
图4　硬黏土应力灵敏度与孔隙指数差的关系

4硬黏土压缩曲线计算模型

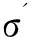
(9)

将式(7)和(8)代入式(9)中,可得

(10)

(11)

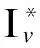
(12)

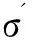
(13)

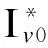
(14)

(15)

将式(13)代入式(12)中，可得

(16)

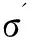
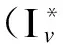
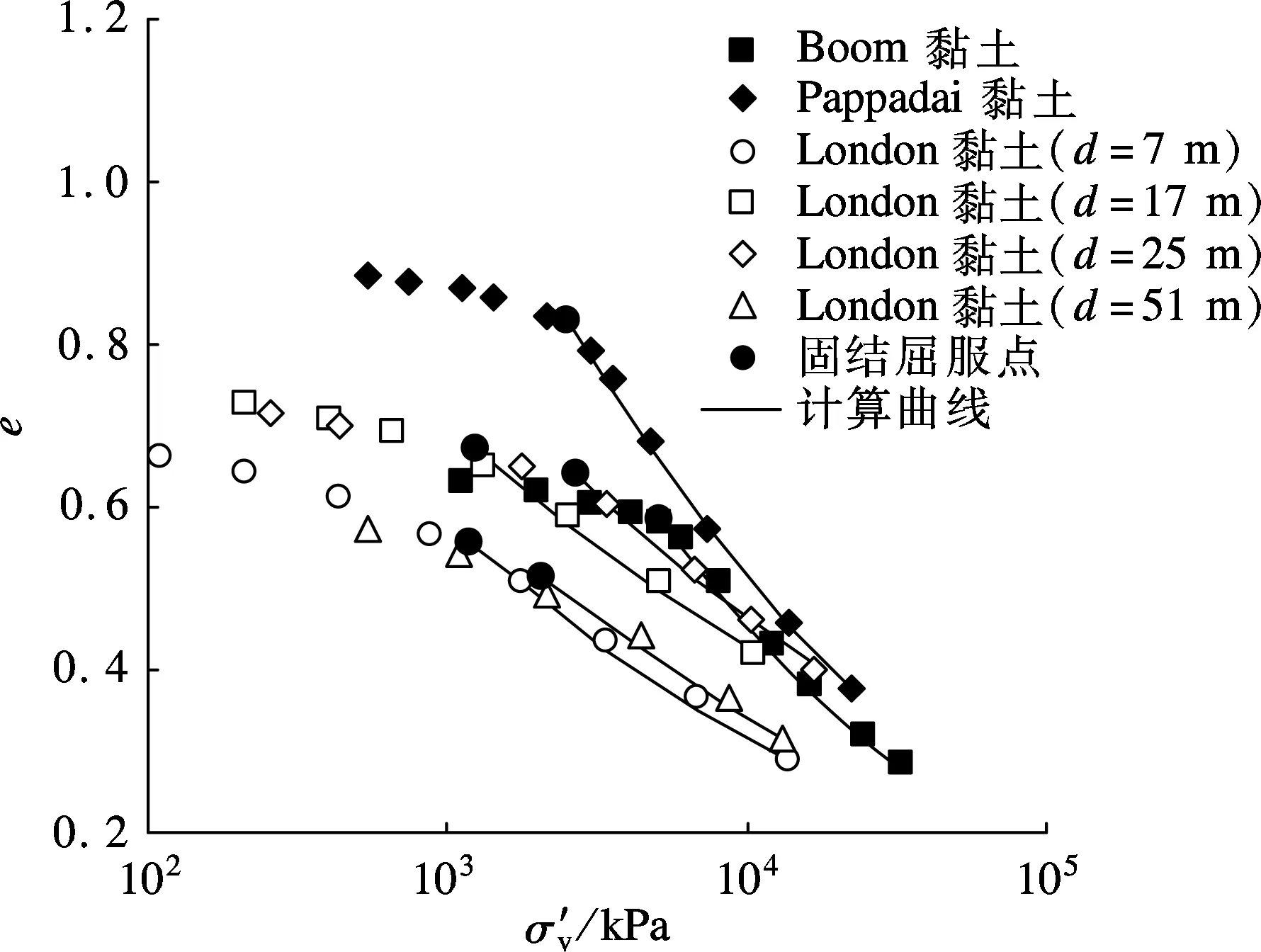
(a) 文献[6,9,11]中的试验数据

(b) 文献[12-13]中的试验数据

5结论

1) 以具有相同超固结比的固有压缩线作为评价硬黏土应力灵敏度的基准线,重新定义了考虑超固结比影响的硬黏土应力灵敏度,从而解决了受超固结比影响的硬黏土压缩曲线与固有压缩线ICL间初始状态不一致对土结构性定量评价影响的问题．

3) 基于考虑超固结比影响的应力灵敏度变化规律,提出了硬黏土屈服后阶段压缩曲线的计算模型,并且通过收集的天然沉积硬黏土一维压缩试验数据验证了其有效性．

参考文献 (References)

[1]WongsarojJ,SogaK,MairRJ.Tunnelling-inducedconsolidationsettlementsinLondonclay[J]. Géotechnique, 2013, 63(13):1103-1115.DOI:10.1680/geot.12.p.126.

[2]CuiYJ,LeTT,TangAM,etal.Investigatingthetime-dependentbehaviourofBoomclayunderthermomechanicalloading[J]. Géotechnique, 2009, 59(4):319-329.DOI:10.1680/geot.2009.59.4.319.

[3]郭杨, 崔伟.PHC管桩在老黏土地区应用的试验研究[J]. 岩土工程学报, 2011, 33(S2): 108-115.

GuoYang,CuiWei.ExperimentalstudyonapplicationofPHCpilesinpaleo-clayarea[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(S2): 108-115. (inChinese)

[4]周健, 简琦薇. 循环荷载下老黏土的动力特性试验研究[J]. 地下空间与工程学报, 2013, 9(6): 1248-1256.

ZhouJian,JianQiwei.ThedynamicresponseofoldcohesivesoilinWuhanundercyclicloading[J]. Chinese Journal of Underground Space and Engineering, 2013, 9(6): 1248-1256. (inChinese)

[5]廖济川. 硬黏土抗剪强度的研究现状[J]. 岩土工程学报, 1990, 12(4): 89-99.

MiaoJichuan.Researchstatusofshearstrengthforstiffclays[J]. Chinese Journal of Geotechnical Engineering, 1990, 12(4): 89-99. (inChinese)

[6]BurlandJB.Onthecompressibilityandshearstrengthofnaturalclays[J]. Géotechnique, 1990, 40(3):329-378.DOI:10.1680/geot.1990.40.3.329.

[7]ChandlerRJ.Thethirdglossoplecture:Claysedimentsindepositionalbasins:Thegeotechnicalcycle[J]. Quarterly Journal of Engineering Geology and Hydrogeology, 2000, 33(1):7-39.DOI:10.1144/qjegh.33.1.7.

[8]ChandlerRJ.Stiffsedimentaryclays:Geologicaloriginsandengineeringproperties[J]. Géotechnique, 2010, 60(12): 891-902.DOI:10.1680/geot.07.kp.001.

[9]GasparreA,CoopMR.Quantificationoftheeffectsofstructureonthecompressionofastiffclay[J]. Canadian Geotechnical Journal, 2008, 45(9):1324-1334.DOI:10.1139/t08-052.

[10]CotecchiaF,ChandlerRJ.Ageneralframeworkforthemechanicalbehaviourofclays[J]. Géotechnique, 2000, 50(4):431-447.DOI:10.1680/geot.2000.50.4.431.

[11]CotecchiaF,ChandlerRJ.Theinfluenceofstructureonthepre-failurebehaviourofanaturalclay[J]. Géotechnique, 1997, 47(3):523-544.DOI:10.1680/geot.1997.47.3.523.

[12]BurlandJB,RampelloS,GeorgiannouVN,etal.Alaboratorystudyofthestrengthoffourstiffclays[J]. Géotechnique, 1996, 46(3):491-514.DOI:10.1680/geot.1996.46.3.491.

[13]MeriggiR,ParonuzziP,SimeoniL.EngineeringgeologycharacterizationoflacustrineoverconsolidatedclaysinanalpineareaofItaly[J]. Canadian Geotechnical Journal, 2000, 37(6):1241-1251.DOI:10.1139/t00-059.

Variationlawofstresssensitivityforstiffclayconsideringeffectsofoverconsolidationratio

BianXia1,2DingJianwen3ShiJian3

(1KeyLaboratoryofMinistryofEducationforGeomechanicsandEmbankmentEngineering,HohaiUniversity,Nanjing210098,China) (2GeotechnicalResearchInstitute,HohaiUniversity,Nanjing210098,China) (3InstituteofGeotechnicalEngineering,SoutheastUniversity,Nanjing210096,China)

Abstract:To analyze the influences of soil structure on the mechanical behaviors of overconsolidated stiff clay, the intrinsic compression line considering the effect of the overconsoildaiton ratio is proposed. Accordingly, the stress sensitivity of stiff clay considering the effect of the overconsoildaiton ratio is redefined. By coupling the effects of soil structure and overconsolidation on the mechanical behaviors of overconsolidated stiff clay and extending the definition of stress sensitivity from single stress level to current stress level, the variation law of the stress sensitivity considering the effect of the overconsoildaition ratio with the stress level is investigated. The results show that in the semi-logarithm plot, there is a good linear relationship between the stress sensitivity of stiff clay considering the effect of the overconsolidation ratio and the intrinsic void index. The variation law of the stress sensitivity of different stiff clays with the stress level can be normalized by the void index difference. Based on the variation law of the stress sensitivity of stiff clay considering the effect of the overconsoildaition ratio, a computation model of the compression line for natural stiff clay at the post-yield state is also proposed.

Key words:stiff clay; soil structure; stress sensitivity; overconsolidation ratio

DOI:10.3969/j.issn.1001-0505.2016.03.028

收稿日期:2016-01-18.

作者简介:卞夏(1988—)，男，博士；丁建文(联系人)，男，博士，副教授， jwding@seu.edu.cn.

基金项目:国家自然科学基金资助项目(41372309，41502263)、江苏省自然科学基金资助项目(BK20150819)、中央高校基本科研业务费专项资金资助项目(2015B00914)、“十二五”国家科技支撑计划资助项目(2015BAB07B06).

中图分类号:TU 41

文献标志码:A

文章编号:1001-0505(2016)03-0624-05

引用本文: 卞夏,丁建文,史剑.考虑超固结比影响的硬黏土应力灵敏度变化规律[J].东南大学学报(自然科学版),2016,46(3):624-628.DOI:10.3969/j.issn.1001-0505.2016.03.028.