高阶多元直觉模糊时间序列预测模型

王亚男　 雷英杰　 雷　阳　 范晓诗

(1空军工程大学防空反导学院, 西安 710051)(2武警工程大学电子技术系, 西安 710086)

高阶多元直觉模糊时间序列预测模型

王亚男1雷英杰1雷阳2范晓诗1

(1空军工程大学防空反导学院, 西安 710051)(2武警工程大学电子技术系, 西安 710086)

摘要:为了突破模糊集理论的限制,更客观地描述不确定性数据,提出一种高阶多元直觉模糊时间序列预测模型．采用模糊聚类算法划分论域，并采用更具客观性的方法建立直觉模糊集的隶属度和非隶属度函数．依据直觉模糊多维取式推理的原理建立基于相似度量的启发式推理规则,作为高阶多元模型的预测规则,并且建立相应的解模糊方法．利用北京市日均气温数据集进行对比实验,结果表明，该模型的预测均方误差(0.86)和平均预测误差(2.57%)较现有方法均明显降低,预测结果优于模糊时间序列预测模型和普通直觉模糊时间序列预测模型．

关键词:高阶;多元;直觉模糊时间序列;直觉模糊多维取式推理

模糊时间序列(fuzzytimeseries,FTS)预测理论是Song等[1]于1993年首次提出的,此后该理论在预测领域(尤其是不精确数据、模糊数据或者数据发展趋势不明确的预测问题)中得到了广泛研究与发展,例如股指预测[2]和环境污染物浓度预测[3]等．FTS预测模型的研究主要集中在3个方面:① 论域划分方法．从初期的等分划分方法改进到非等分划分方法,根据历史数据的分布特征,采用基于概率分布的算法[4]、基于信息粒的算法[5]和聚类算法[6]等对论域进行划分,有效提高了预测精度．② 模糊关系和预测规则．从初期的“取大-取小”运算进化到基于神经网络方法[7]、粒子群算法[8]和矢量量化技术[9]的方法等,使模型的预测精度得到很大提升．③ 多元和高阶模型．先后出现了基于禁忌搜索算法[10]、基于人工神经网络[11]和基于关系组算法[12]等的多种高阶和多元模型,显著增强了FTS模型的适应性．

FTS模型采用传统的Zadeh模糊集对历史数据进行模糊化,即仅用隶属度来度量语言值的隶属性质,不够全面、客观,从根本上限制了预测精度的提升．而直觉模糊集引入直觉指数这一指标使得对数据的描述更加客观和细腻,因此Castillo等[13]首次将直觉模糊集理论融入时间序列分析,建立了一个直觉模糊推理系统进行预测．但这个系统本质上仍是2个隶属度模糊推理系统和非隶属度模糊推理系统的加权合成．Joshi等[14]以FTS模型为基础,建立了一个直觉模糊时间序列(intuitionisticfuzzytimeseries,IFTS)预测模型,但模型使用的直觉模糊集隶属度和非隶属度函数的确定方法存在固有缺陷．郑寇全等[15-16]利用直觉模糊C均值聚类算法实现论域的自适应划分,同时引入矢量量化技术有效提高了预测精度,但是如何有效地直觉模糊化历史数据,使其符合直觉模糊C均值聚类算法的应用条件,在模型中依然没有给出很好的解释．

直觉模糊集理论的引入极大地扩展了时间序列对模糊信息的处理能力,为模糊时间序列研究开辟了新的研究方向．然而,当前IFTS理论的研究较少,国内外仅有的研究理论深度不够,预测精度有待进一步提高．鉴于此,本文从论域划分、直觉模糊集建立和预测规则3个方面进行改进,重点建立以直觉模糊多维取式推理为基础的预测规则,提出了一个高阶多元IFTS预测模型．通过对比试验,证明所建模型有效克服了FTS预测理论的缺陷,取得了较好的预测结果．

1基本概念

定义1设X是一给定论域,则X上的一个直觉模糊集A为

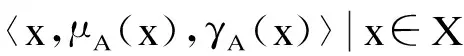
(1)

式中,μA(x):X→[0,1]和γA(x):X→[0,1]分别为A的隶属度和非隶属度函数,且∀x∈X,有0≤μA(x)+γA(x)≤1,称πA(x)=1-μA(x)-γA(x)为x的直觉指数,它是x对A的犹豫程度的测度．

定义2设X和Y是普通有限非空集合或论域．定义在直积空间X×Y上的直觉模糊子集R为从X到Y之间的二元直觉模糊关系．记为

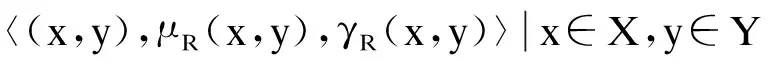
(2)

式中,μA(x,y):X×Y→[0,1],γA(x,y):X×Y→[0,1]满足条件0≤μR(x,y)+γR(x,y)≤1,∀(x,y)∈X×Y．

定义3设论域X(t) (t=1,2,…)为R的一个子集,fi(t)=〈μi(X(t)),γi(X(t))〉(i=1,2,…)为定义在X(t)上的直觉模糊集,若F(t)={f1(t),f2(t),…},则称F(t)为定义在X(t)上的直觉模糊时间序列．

定义4令F(t)为定义在X(t)上的直觉模糊时间序列．设R(t,t-1)为从F(t-1)到F(t)的直觉模糊关系,且满足F(t)=F(t-1)∘R(t,t-1),即F(t)是由F(t-1)通过直觉模糊关系R(t,t-1)推导得到的,其中“∘”表示直觉模糊合成运算,则称R(t,t-1)为F(t)上的一阶直觉模糊逻辑关系,可表示为

F(t-1)→F(t)

(3)

式中,F(t-1)和F(t)分别称为关系的前件和后件．

定义5令F(t)为定义在X(t)上的直觉模糊时间序列．若F(t)由F(t-1),F(t-2),…,F(t-k)共同推导得到,它们之间的直觉模糊逻辑关系可表示为

F(t-k),…,F(t-2),F(t-1)→F(t)

(4)

则称F(t)为一元k阶直觉模糊时间序列．

定义6令F1(t),F2(t),…,Fm(t)和F(t)为m+1个直觉模糊时间序列．如果F(t)由F1(t-1),F1(t-2),…,F1(t-k),F2(t-1),F2(t-2),…,F2(t-k),…,Fm(t-1),Fm(t-2),…,Fm(t-k)共同推导得到,则它们之间的直觉模糊逻辑关系可表示为

(F1(t-k),F2(t-k),…,Fm(t-k)),…,

(F1(t-2),F2(t-2),…,Fm(t-2)),

(F1(t-1),F2(t-1),…,Fm(t-1))→F(t)

(5)

因此称F(t)为k阶m元直觉模糊时间序列．

在k阶m元直觉模糊时间序列中,通常存在一个主元数据和m-1个次元数据．

2高阶多元直觉模糊时间序列预测模型

2.1基于模糊聚类的非等分论域划分

在k阶m元IFTS模型中,每一元数据都有一个独立论域,因此需要确定m个论域:U1,U2,…,Um．但每一元数据的论域确定方法及划分方法都是相同的．令U=[xmin-ε1,xmax+ε2],其中xmin和xmax分别表示历史数据的最小值和最大值;ε1和ε2是2个合适的正数,使得xmin和xmax分别向下、向上取合适整数．

在论域划分上,本文采取了较遗传算法等优化算法更简捷、更具实时性的基于最大生成树的直接模糊聚类算法[17]．利用该算法聚类得到的r类数据可记为

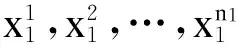
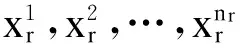
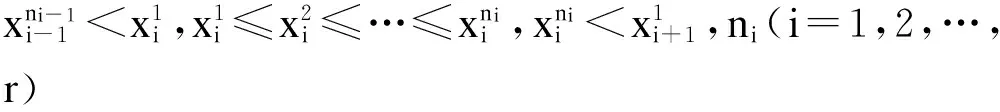
(6)

则论域U被划分成的r个非等长区间可表示为

u1=[d0,d1],u2=[d1,d2], …,ur=[dr-1,dr]

2.2历史数据直觉模糊化

对应于论域U的r个区间,定义r个代表语言

变量的直觉模糊集:

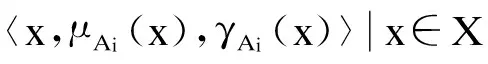
(7)

式中,i=1,2,…,r．确定Ai的隶属度和非隶属度函数是该步骤的关键．受直觉指数的影响,确定直觉模糊集的隶属度和非隶属度函数的方法具有极大的复杂性．已有方法如模糊统计法、三分法等多将直觉指数固定为一个常数[18],有失客观性．针对IFTS模型中历史数据的实际情况及划分特性,作者在前期研究中提出一种更具客观性的隶属度和非隶属度函数的确定方法[19],由于篇幅所限,本文只引用其计算结果,具体过程不再赘述．将历史数据的直觉模糊化结果记为

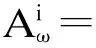
(8)

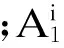
2.3直觉模糊逻辑关系和预测规则建立

2.3.1高阶多元直觉模糊逻辑关系

对历史数据直觉模糊化后,定义6中的k阶m元直觉模糊逻辑关系可表示为

(9)

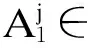
从n个历史数据中能得到n-k个k阶m元直觉模糊逻辑关系,如表1第2列所示．

表1　历史数据的k阶m元直觉模糊逻辑关系

2.3.2直觉模糊多维取式推理

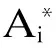
规则:IFxisA1×A2×…×AnTHENyisB．

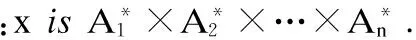
输出:yisB*．

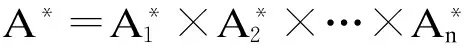
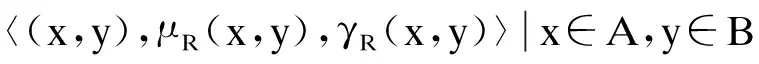
(10)

其中

μR(x,y)=μA(x)∧μB(y)

(11)

γR(x,y)=γA(x)∨γB(y)

(12)

μA(x)=μA1(x)∧μA2(x)∧…∧μAn(x)

(13)

γA(x)=γA1(x)∨γA2(x)∨…∨γAn(x)

(14)

推理输出为

B*=A*∘R

(15)

其中，直觉模糊合成运算“∘”采用取大“∨”、取小“∧”运算，即

(16)

(17)

(18)

(19)

2.3.3基于直觉模糊推理的预测规则

模糊规则的建立分为以下3个步骤:

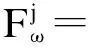
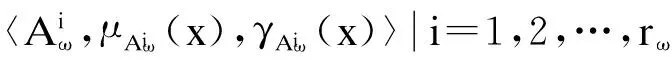
(20)

相应地,直觉模糊逻辑关系即式(9)也应变成

(21)

所有直觉模糊逻辑关系变形后如表1第3列所示．

步骤2寻找相似直觉模糊逻辑关系．分别计算表1第3列中各关系式前件与式(21)前件的相似度,其中具有最大相似度的关系式就是与式(21)相似的直觉模糊逻辑关系．记表1第3列中第α(1≤α≤t-k)个直觉模糊逻辑关系为

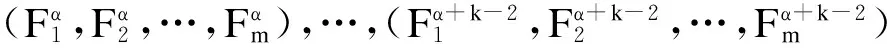
(22)

则式(21)和式(22)的前件相似度S(α,t-k)为

(23)

(24)

(25)

计算得到的相似直觉模糊逻辑关系可记为

(26)

步骤3进行直觉模糊推理,得到直觉模糊化预测结果．将式(26)的前件作为2.3.2节中直觉模糊多维取式推理的推理规则,式(21)的前件作为推理输入,可得到m个推理模型．

模型ω

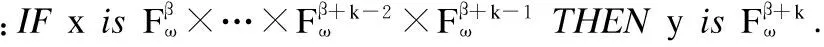
按照式(10)～(19)计算模型ω(ω=1,2,…,m)的推理结果,在结果中,拥有最大隶属度的元素即为由该模型得到的直觉模糊化预测结果．由模型ω得到的直觉模糊化预测结果可记为

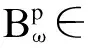
(27)

式中,p=1,2,…,Pω;ω=1,2,…,m;Pω为第ω个模型的预测结果个数．

以模型1为例,其推理结果为

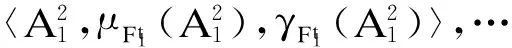
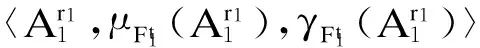
(28)

2.4预测结果去直觉模糊化

去直觉模糊化过程的具体步骤如下:

步骤1模型1得到的直觉模糊化预测结果是IFTS序列的主元,对其直接去直觉模糊化．直觉模糊集的去直觉模糊化算法通常有重心法、加权平均法和最大真值法等．由于重心法具有比较平滑的输出控制,及对应于输入信号的微小变化输出也会发生一定的变化,且这种变化明显比较平滑,因此本节采用重心法计算[18],即

(29)

模型1的去直觉模糊化预测结果为P1个元素的去直觉模糊化结果的均值,即

(30)

步骤2模型2～模型m得到的直觉模糊化预测结果是IFTS序列的次元,需要将其转化为主元结果．将模型2～模型m得到的直觉模糊化预测结果进行组合,可得到P2×…×Pm种组合:

(31)

步骤3主元和次元结果合成输出．取f1和f2,…,m的均值作为模型的最终预测结果．

(32)

当2.3.3节中得到的相似直觉模糊逻辑关系不唯一,即式(26)包含多个直觉模糊逻辑关系时,需要对每个相似直觉模糊逻辑关系按照2.3.3节和2.4节的步骤进行计算,分别得到各自的预测结果后取平均值作为最终预测结果．

3模型应用

北京市日均气温数据集是以天为单位对北京市气温进行统计得到的,其中日均气温(mean temperature, MTP)为序列的主元,日照时数(sunshine duration, SSD)和气温日较差(diurnal temperature range, DTR)为影响日均气温的2个次元．本文选取2014-06-01—2014-06-30的30组数据作为历史数据,以三阶三元模型为例预测2014-07-01的日均气温．所有数据如表2所示．

2014-07-01日均气温预测的具体步骤如下:

步骤1MTP, SSD和DTR的论域分别为U1=[20,30],U2=[1,14],U3=[6,17]．各区间划分结果如表3所示．

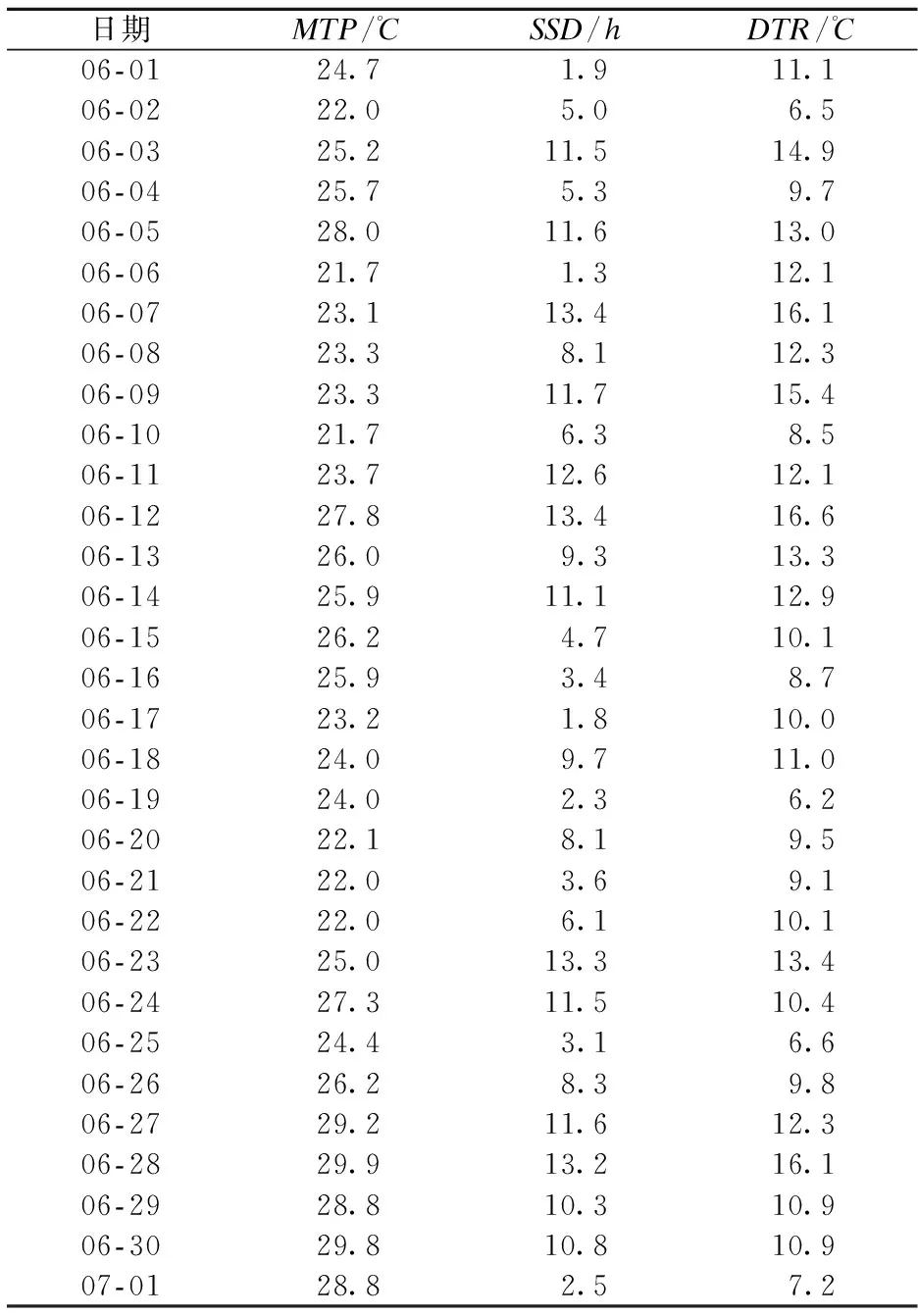
表2　2014-06-01—2014-07-01北京市日均气温

表3　MTP, SSD和DTR的区间划分

步骤2对应于MTP,SSD和DTR的划分区间,分别建立9个直觉模糊集,即Ai,Bi和Ci(i=1,2,…,9)．将30组历史数据直觉模糊化．

步骤3将2014-07-01的MTP,SSD和DTR对应的直觉模糊集分别记为At,Bt和Ct,则它们与其前3天数据之间的直觉模糊逻辑关系为

(A9,B9,C8),(A7,B7,C3),(A9,B7,C3)→At

(33)

变形后为

(F28,G28,H28),(F29,G29,H29),(F30,G30,H30)→Ft

(34)

同时,可以由历史数据得到27个三阶三元直觉模糊逻辑关系,如表4第2列所示,变形后如表4第3列所示．

表4　MTP, SSD和DTR历史数据的直觉模糊逻辑关系

经计算,与式(34)相似的直觉模糊逻辑关系为

(F27,G27,H27),(F28,G28,H28),(F29,G29,H29)→F30

(35)

将式(35)的前件作为推理规则,式(34)的前件作为推理输入,则可以得到3个推理模型,分别为

模型1

规则:IFxisF27×F28×F29THENyisF30．

输入:xisF28×F29×F30．

输出:yisFt．

模型2

规则:IFxisG27×G28×G29THENyisG30．

输入:xisG28×G29×G30．

输出:yisGt．

模型3

规则:IFxisH27×H28×H29THENyisH30．

输入:xisH28×H29×H30．

输出:yisHt．

模型1的输出Ft中隶属度最大的元素为A8和A9;模型2的输出Gt中隶属度最大的元素为B7;模型3的输出Ht中隶属度最大的元素为C2,C3,C4和C5．

步骤4预测结果去直觉模糊化．

① 对模型1的推理结果去直觉模糊化,即

(36)

② 对模型2和模型3的推理结果合并去直觉模糊化．在表4第2列中寻找包含模型2和模型3预测结果组合的直觉模糊集组合,得到

(A6,B7,C5),(A4,B7,C5),(A5,B7,C2),

(A8,B7,C4),(A7,B7,C3),(A9,B7,C3)

(37)

取直觉模糊集A6,A4,A5,A8,A7,A9对应区间中值的均值作为主元结果,即

f2,3=28.15

(38)

③ 主元和次元结果合成输出．取f1和f2,3的均值作为模型的最终预测结果,即

(39)

则2014-07-01日均气温的预测结果为28.83 ℃．

应用文献[1,11,14]中的模型及本文模型对北京市日均气温数据集的所有数据进行预测,得到各模型的预测值及实际值如图1所示．其中,文献[1]为传统FTS模型;文献[11]为高阶FTS预测模型,文中作者选择的最优预测结果所对应的“200-4-second order”模型将论域划分为35个区间,这在实际操作中会带来极大的工作量,是不现实的,因此本文在保证计算合理的基础上，选则其性能最优的“700-4-second order”模型进行比较;文献[14]为一阶IFTS预测模型,因为现有IFTS预测模型中并没有高阶模型,因此只能与一阶模型进行比较．

图1　各模型对日均气温数据集的预测结果

根据均方误差(RMSE)和平均预测误差(AFE)这2项指标对各模型的预测性能进行检验.指标的计算公式如下:

(40)

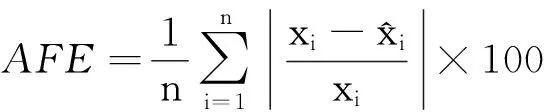
(41)

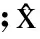
表5　各模型对日均气温数据集的预测性能

由表5可知,该模型的预测均方误差为0.86，平均预测误差为2.57%.这表明本文所建高阶IFTS模型能够有效预测通用数据集中的数据,预测效果较现有模型有了较大提升,证明该模型具有很强的可行性和有效性．

4结语

本文针对模糊时间序列预测方法的不足,利用直觉模糊集在处理不确定数据集上的优势,建立了一个新的高阶多元直觉模糊时间序列预测模型．采用基于最大支撑树的模糊聚类算法实现论域的非等分划分,使得论域划分这一基础步骤更具实时性和简捷性;采用基于相似度量的启发式直觉模糊多维取式推理建立序列数据的预测规则,更有效地预测不确定数据的模糊变化特征．在北京市日均气温数据集上与经典算法的对比实验表明，该模型具有较好的预测性能．如何优化直觉模糊推理过程,进一步提高预测性能,将是下一步研究的重点．

参考文献 (References)

[1]SongQ,ChissomBS.Forecastingenrollmentswithfuzzytimeseries—PartⅠ[J]. Fuzzy Sets and Systems, 1993, 54(1):1-9.DOI:10.1016/0165-0114(93)90355-1.

[2]SunB,GuoH,KarimiHR,etal.Predictionofstockindexfuturespricesbasedonfuzzysetsandmultivariatefuzzytimeseries[J]. Neurocomputing, 2015, 151(3): 1528-1536.DOI:10.1016/j.neucom.2014.09.018.

[3]DomańskaD,WojtylakM.Applicationoffuzzytimeseriesmodelsforforecastingpollutionconcentrations[J]. Expert Systems with Applications, 2012, 39(9): 7673-7679.DOI:10.1016/j.eswa.2012.01.023.

[4]HuarngK,YuTHK.Ratio-basedlengthsofintervalstoimprovefuzzytimeseriesforecasting[J]. IEEE Transactions on Systems, Man, and Cybernetics—Part B: Cybernetics, 2006, 36(2): 328-340.

[5]LuW,ChenX,PedryczW,etal.Usingintervalinformationgranulestoimproveforecastinginfuzzytimeseries[J]. International Journal of Approximate Reasoning, 2015, 57:1-18.DOI:10.1016/j.ijar.2014.11.002.

[6]LiuJW,ChenTL,ChengCH,etal.Adaptive-expectationbasedmulti-attributeFTSmodelforforecastingTAIEX[J]. Computers & Mathematics with Applications, 2010, 59(2):795-802.DOI:10.1016/j.camwa.2009.10.014.

[7]KhasheiM,HejaziSR,BijariM.Anewhybridartificialneuralnetworksandfuzzyregressionmodelfortimeseriesforecasting[J]. Fuzzy Sets and Systems, 2008, 159(7): 769-786.DOI:10.1016/j.fss.2007.10.011.

[8]SinghP,BorahB.ForecastingstockindexpricebasedonM-factorsfuzzytimeseriesandparticleswarmoptimization[J]. International Journal of Approximate Reasoning, 2014, 55(3):812-833.DOI:10.1016/j.ijar.2013.09.014.

[9]LiST,KuoSC,ChengYC,etal.Deterministicvectorlong-termforecastingforfuzzytimeseries[J]. Fuzzy Sets and Systems, 2010, 161(13):1852-1870.DOI:10.1016/j.fss. 2009.10.028.

[10]AvazbeigiM,DoulabiSHH,KarimiB.Choosingtheappropriateorderinfuzzytimeseries:AnewN-factorfuzzytimeseriesforpredictionoftheautoindustryproduction[J]. Expert Systems with Applications, 2010, 37(8):5630-5639.DOI:10.1016/j.eswa.2010.02.049.

[11]AladagCH,BasaranMA,EgriogluE,etal.Forecastinginhighorderfuzzytimesseriesbyusingneuralnetworkstodefinefuzzyrelations[J]. Expert Systems with Applications, 2009, 36(3):4228-4231.DOI:10.1016/j.eswa.2008.04.001.

[12]ChenSM,ChenSW.Fuzzyforecastingbasedontwo-factorsecond-orderfuzzy-trendlogicalrelationshipgroupsandtheprobabilitiesoftrendsoffuzzylogicalrelationships[J]. IEEE Transactions on Cybernetics, 2015, 45(3): 405-417.DOI:10.1109/TCYB.2014.2326888.

[13]CastilloO,AlanisA,GarciaM,etal.Anintuitionisticfuzzysystemfortimeseriesanalysisinplantmonitoringanddiagnosis[J]. Applied Soft Computing, 2007, 7(4): 1227-1233.DOI:10.1016/j.asoc.2006.01.010.

[14]JoshiBP,KumarS.Intuitionisticfuzzysetsbasedmethodforfuzzytimeseriesforecasting[J]. Cybernetics and Systems: An International Journal, 2012, 43(1): 34-47.

[15]郑寇全, 雷英杰, 王睿, 等. 直觉模糊时间序列建模及应用[J]. 控制与决策, 2013, 28(10): 1525-1530.

ZhengKouquan,LeiYingjie,WangRui,etal.ModelingandapplicationofIFTS[J]. Control and Decision, 2013, 28(10): 1525-1530. (inChinese)

[16]郑寇全, 雷英杰, 王睿, 等. 基于矢量量化的长期直觉模糊时间序列预测[J]. 吉林大学学报(工学版), 2014, 44(3):795-800.DOI:10.13229/j.cnki.jdxbgxb201403034.

ZhengKouquan,LeiYingjie,WangRui,etal.Long-termintuitionisticfuzzytimeseriesforecastingbasedonvectorquantization[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(3):795-800.DOI:10.13229/j.cnki.jdxbgxb201403034.(inChinese)

[17]梁保松, 曹殿立. 模糊数学及其应用[M]. 北京: 科学出版社, 2007: 75-77.

[18]雷阳. 基于直觉模糊核匹配追踪的目标识别方法研究[D]. 西安:空军工程大学防空反导学院, 2012.

[19]WangYN,LeiYJ,FanXS,etal.Intuitionisticfuzzytimeseriesforecastingmodelbasedonintuitionisticfuzzyreasoning[J]. Mathematical Problems in Engineering, 2016, 2016: 1-12.DOI:10.1155/2016/5035160.

[20]雷英杰, 赵杰, 路艳丽, 等. 直觉模糊集理论及应用:上册[M]. 北京: 科学出版社, 2014: 145-155.

High-ordermulti-variableintuitionisticfuzzytimeseriesforecastingmodel

WangYanan1LeiYingjie1LeiYang2FanXiaoshi1

(1AirandMissileDefenseCollege,AirForceEngineeringUniversity,Xi’an710051,China) (2DepartmentofElectronicsTechnology,EngineeringUniversityofArmedPoliceForce,Xi’an710086,China)

Abstract:In order to break the limitation of fuzzy set theory and objectively describe the uncertain data, a high-order multi-variable intuitionistic fuzzy time series forecasting model is proposed. A fuzzy clustering algorithm is adopted to partition the universe of discourse, and a more objective method is used to establish the membership and non-membership functions of intuitionistic fuzzy sets. According to the principle of multidimensional intuitionistic fuzzy modus ponens reasoning, a heuristic similarity-based reasoning technique is proposed as the forecasting rule of the high-order multi-variable forecasting model, and a corresponding defuzzification method is presented. Contrast experiments on the daily mean temperature of Beijing were carried out. Experimental results show that the root mean square error (0.86) and the average forecasting error (2.57%) of the proposed model both obviously decreased. Therefore, the forecasting performance of the model is better than that of the fuzzy time series forecasting models and the normal intuitionistic fuzzy time series forecasting models.

Key words:high-order; multi-variables; intuitionistic fuzzy time series; multidimensional intuitionistic fuzzy modus ponens reasoning

DOI:10.3969/j.issn.1001-0505.2016.03.009

收稿日期:2015-09-23.

作者简介:王亚男(1988—)，女，博士生；雷英杰(联系人)，男，博士，教授，博士生导师，leiyjie@163.com.

基金项目:国家自然科学基金青年科学基金资助项目(61309022).

中图分类号:TP393.08

文献标志码:A

文章编号:1001-0505(2016)03-0505-08

引用本文: 王亚男,雷英杰,雷阳,等.高阶多元直觉模糊时间序列预测模型[J].东南大学学报(自然科学版),2016,46(3):505-512.DOI:10.3969/j.issn.1001-0505.2016.03.009.