数字闭环光纤陀螺振动噪声处理方法

宋　锐　　陈熙源

(东南大学仪器科学与工程学院,南京210096)(东南大学微惯性仪表与先进导航技术教育部重点实验室,南京210096)

数字闭环光纤陀螺振动噪声处理方法

宋锐陈熙源

(东南大学仪器科学与工程学院,南京210096)(东南大学微惯性仪表与先进导航技术教育部重点实验室,南京210096)

摘要:为了解决数字闭环光纤陀螺在实际工程应用中易受冲击、振动等环境因素影响的问题,通过分析振动影响下陀螺输出信号特点,研究振动对光纤环的应力及信号中附加相移的影响,建立了光纤陀螺信号的振动噪声模型.首先,引入一种具有自适应能力的改进局部均值分解方法,将原信号按频率大小分解为一系列谐波信号;其次,利用核主成分分析方法,将反映振动影响的有效信号和噪声进行有效分离;然后,通过重构得到抑制了振动噪声的信号.利用线振动实验研究了光纤陀螺在车载和机载环境下的振动特性,并对采集得到的10组振动实验数据进行了分析.结果表明,处理后信号的Allan方差分析结果中量化噪声和零偏不稳定性等误差系数均减小约50%,从而有效提高了光纤陀螺在振动环境下的输出精度.

关键词:光纤陀螺;振动误差;核主成分分析

光纤陀螺是惯性系统中广泛采用的一种全固态角速度测量器件,其性能水平对惯性系统的精度存在较大影响.理论上,光纤陀螺的全固态、无运动部件等特点,使其与传统机械陀螺相比具有抗冲击、抗振动等优势;然而,鉴于光纤的弹光效应,在实际工程应用中,冲击、振动等环境因素会引起光纤环的应力产生变化,器件尾纤振动以及结构的共振都将引起陀螺误差,从而导致振动状态下器件的动态误差增加.为了提高控制系统的精度,需要对振动等复杂环境下的光纤陀螺输出信号特点开展研究.

根据典型干涉式数字闭环光纤陀螺的基本原理[1],结合已有的研究成果发现,光纤缺陷以及因光纤、器件尾纤长度、折射率和折损等变化而产生的寄生应力[2],会引起系统回路中传输光偏振性能和光功率变化,进而产生测量误差.

目前,抑制光纤陀螺振动误差的方法主要包括改善封装结构、控制黏结剂涂覆用量、加入橡胶减振装置、光纤环采用四极对称绕法、对信号进行调制等[3],但受安装工艺等方面的限制,这些改进措施的效果会受到影响,关于振动情形下光纤陀螺的信号表现形式以及环路改进后系统中的振动误差建模补偿，还需进行进一步深入的研究.对于具有非平稳性、非线性特征的陀螺振动信号,研究者们常采用小波变换[4]进行处理,但小波阈值消噪时需设定小波基、分界层数、阈值等参数,缺乏根据输入数据自适应优化的能力.

本文针对现有技术的不足,基于陀螺振动信号的特点,引入了一种改进的局域均值分解(LMD)方法[5].在改进检测电路结构等的基础上,按照所提出的改进方法对陀螺振动信号的特征进行分析,将复杂的振动信号分解为若干个乘积函数(PF)的线性组合,每一个PF分量表示原信号中某一频率段的谐波信号.然后,运用核主成分分析(KPCA)方法[6-9]将所得分量中反映振动影响的有效信号和噪声进行分离,进一步重构得到抑制了振动噪声的输出信号,从而提高光纤陀螺的测量精度.

1数字闭环光纤陀螺的基本原理及振动特性分析

干涉式数字闭环光纤陀螺由光路和数字逻辑电路2个部分组成.光路部分主要的光电元器件包括保偏光纤、宽带光源、光电探测组件、耦合器、多功能集成光学器件(MIOC)等[10].

冲击、振动等环境因素下光纤陀螺的光路部分受到应力作用,一方面会产生附加非互易相移,另一方面又会引起光纤中传输光的光功率波动.具体来看,陀螺误差振动影响下光纤陀螺的输出信号I可表示为

I=-4KP0(1+ΔP(fv)cos(ωvt+θ2))·

sin(Δφ+φ(fv)cos(ωvt+θ1))sinφ

(1)

式中,K为系统增益;P0为光源的平均功率幅值;fv为振动频率;ΔP(fv)为受振动影响的光功率幅值;ωv=2πfv为振动角频率;θ2为受振动影响的光功率初始相角; Δφ为含有Sagnac相位差与反馈相位差的相移;φ(fv),θ1分别为受振动影响的非互易相移误差的幅值和初始相角;φ为偏置调制相移.

基于振动环境下光纤陀螺输出信号的表现形式,可进一步提出光纤陀螺振动误差的建模方法.

2改进的LMD 算法

假设原始信号为x(t),改进的LMD算法步骤如下:

① 分别对原始信号x(t)中极大值和极小值进行3次样条插值,形成上包络函数Eu(t)和下包络函数El(t),从而得到局部均值函数值m11(t)和局部包络函数值a11(t),即

(2)

(3)

② 从原始信号中分离出局部均值函数值m11(t)后得到

h11(t)=x(t)-m11(t)

(4)

对h11(t)做进一步解调得到

(5)

③ 根据解调后得到的s11(t),重复步骤①和步骤②,得到对应的局部包络函数值a12(t).将相邻2次迭代得到的差值e小于0作为运算终止条件.若不满足该条件,则重复步骤① 和步骤②,直至第r次运行结果满足条件为止.第j次循环后得到的差值ej可表示为

治疗后，常规组优5例、良27例、中6例、差2例，优良率为80.0%(32/40)；观察组优20例、良18例、中2例，优良率为95.0%(38/40)；观察组优良率显著高于常规组，两组比较，差异有统计学意义(P<0.05)。观察组手术时间、住院时间、并发症发生率均显著低于常规组，两组比较，差异有统计学意义(P<0.05)。见表1。两组患者术前VAS评分、ODI评分比较，差异无统计学意义(P>0.05)；术后观察组的VAS评分与ODI评分均显著优于常规组，且优于治疗前，组间比较，差异有统计学意义(P<0.05)。见表2。典型病例见图1。

(6)

式中,mij(t)为求解第i个PF分量时计算得到的第j次局部均值函数值.

④ 将迭代过程中得到的所有局部包络函数相乘,便可得到纯调频信号的包络信号,即

(7)

包络信号a1(t)与对应调频信号s1r(t)的乘积即为第1个PF分量S1(t),即

S1(t)=a1(t)s1r(t)

(8)

⑤ 若残差信号u1(t)=x(t)-S1(t)不满足单调性,则将u1(t)作为初始信号循环执行步骤①～步骤④,直到第L个残差信号uL(t)是单调函数为止.故原始信号可表示为

(9)

3核主成分分析方法

针对分解得到的高频信号,运用核主成分分析方法进行处理,基本原理如下.

将第q个分量信号表示为Sq={pk}，其中,k=1,2，…,M,pk∈RN,M,N分别为分量参数的个数和维数.

利用非线性函数φ将分量信号所在的输入空间映射到对应的特征空间中.

(10)

对协方差矩阵进行特征值分解可得

CFλF=λFWF

(11)

式中,λF为特征值.所有对应于特征值λF≠0的特征向量WF都处于φ(p1),φ(p2),…,φ(pM)所组成的空间中,则有

λF(φ(pk)·WF)=φ(pk)·CF·WF

k=1,2,…,M

(12)

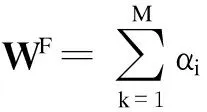
综上可得

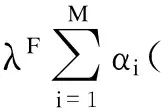
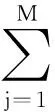
k=1,2,…,M

(13)

定义一个M×M矩阵K(pm,pn),且

K(pm,pn)=φ(pm)·φ(pn)

则式(13)可表示为

MλFK·α=K2·α

(14)

式中,α为α1,α2,…,αM构成的列向量.

式(11)转化为求解式(14)的特征值和特征向量的问题,即

MλFα=K·α

(15)

用λ1≥λ2≥…≥λM表示矩阵K的特征值,则α为其对应的特征向量.

对于输入空间中的点b,其在特征空间F中的像为φ(b),则所求得的主成分为

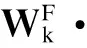
(16)

式(16)计算得到的主成分为分量信号中能量所占比例较大的部分,即消除了高频振动噪声影响的有效信号.通过重构方法便可得到所需的光纤陀螺输出信号.

4实验结果与分析

在实验室条件下,通过线振动实验研究数字闭环光纤陀螺在车载和机载环境下的振动特性.光纤陀螺输出信号如图1所示.

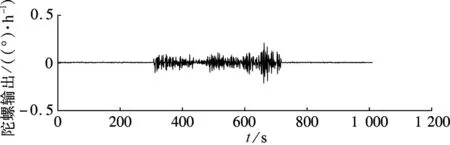
(a) 车载环境

(b) 机载环境

运用改进的LMD方法将信号按照频率大小分解,得到主要分量S1(t)～S4(t)和残差量R(t)(见图2).对于分解得到的高频分量,运用核主成分分析方法将反映振动影响的有效信号和噪声进行有效分离,其中核函数为多项式核函数K(x′,y′)=(x′·y′+1)d,其中x′,y′为函数输入,d为函数阶数.然后,通过重构得到满足要求的输出信号.图3为最终得到的滤除高频噪声的信号和光纤陀螺原始振动信号比较图.由图可知,所提方法对于振动前、振动中和取消振动后的光纤陀螺输出信号均有较好的改善.

(a) 车载环境

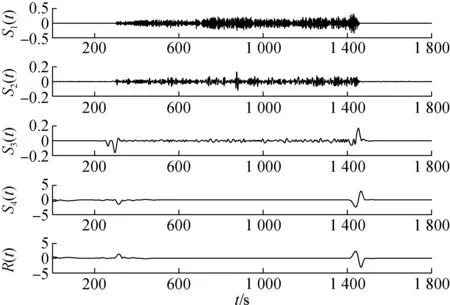
(b) 机载环境

(a) 车载环境

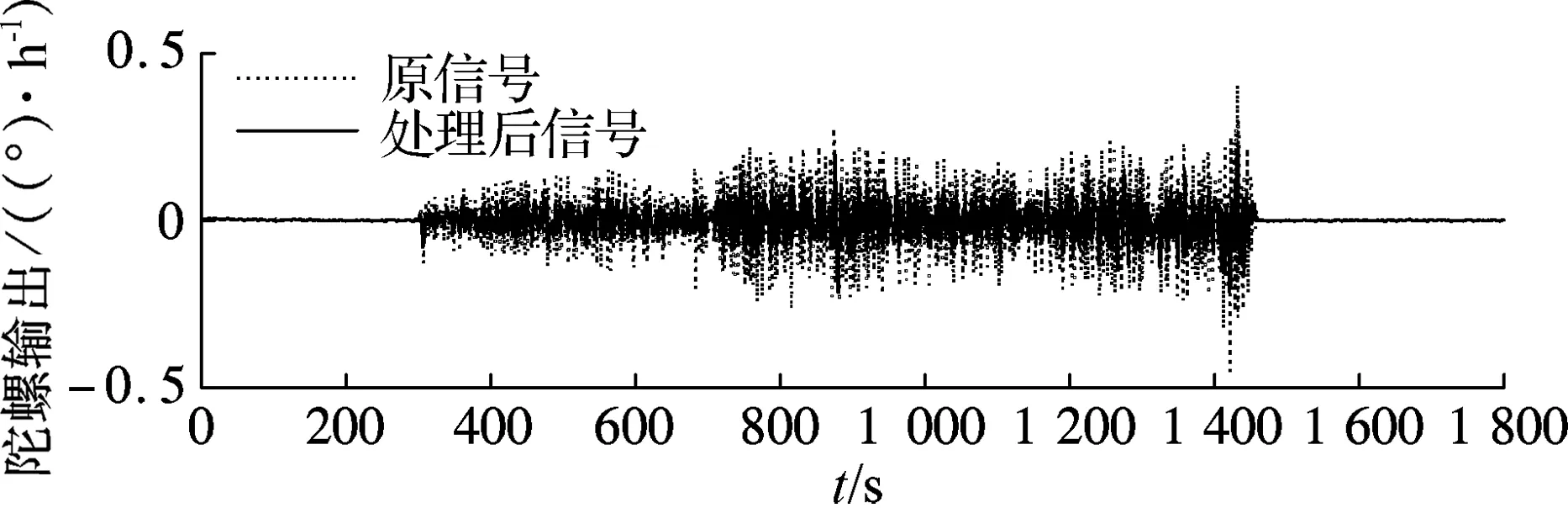
(b) 机载环境

为了进一步验证所提算法的有效性,分别采集10组振动试验下陀螺的输出信号并加以分析.利用Allan方差分析方法对光纤陀螺原始输出信号和经过改进的LMD方法处理后的信号进行量化比较,结果见表1和表2.由表可知,利用改进的LMD方法进行处理后,信号中量化噪声和零偏不稳定性等误差系数均减小约50%,从而提高了光纤陀螺的测量精度.

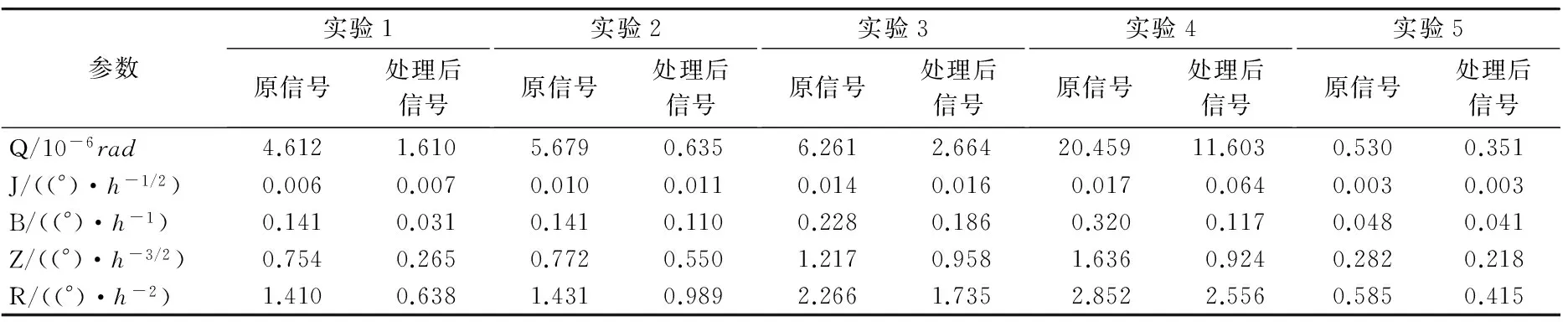
表1　车载环境下原信号及改进LMD方法处理结果的Allan方差分析

注:Q为量化噪声系数;J为角度随机游走系数;B为零偏不稳定性系数;Z为速率随机游走系数;R为速率斜坡系数.

表2　机载环境下原信号及改进LMD方法处理结果的Allan方差分析

5结语

本文从干涉型数字闭环光纤陀螺的基本原理出发,分析了线振动对光纤陀螺输出的影响,提出了一种基于改进局部均值分解的陀螺振动误差建模方法.与小波变换等常见信号处理方法相比,该方法能够运用核主成分分析方法将振动影响下的有效信号和噪声进行分离,有效地抑制了振动影响下光纤陀螺输出中的噪声和漂移.Allan方差分析结果表明,利用所提方法有效地提高了光纤陀螺在振动环境下的输出精度.

参考文献 (References)

[1]OhnoA,MotoharaS,UsuiR,etal.Developmentoffiber-opticgyroscopewithenvironmentalruggedness[C]//Fiber Optic Gyros: 15th Anniversary Conference International Society for Optics and Photonics.Boston,USA,1991, 1585: 82-88.DOI:10.1117/12.135037.

[2]宋凝芳, 张春熹, 李立京, 等. 数字闭环光纤陀螺振动误差分析[J]. 北京航空航天大学学报, 2004, 30(8):702-704.DOI:10.3969/j.issn.1001-5965.2004.08.003.

SongNingfang,ZhangChunxi,LiLijing,etal.Analysisofvibrationerrorindigitalclosed-loopfiberopticgyroscope[J]. Journal of Beijing University of Aeronautics and Astronautics, 2004, 30(8):702-704.DOI:10.3969/j.issn.1001-5965.2004.08.003.(inChinese)

[3]舒建涛, 李绪友, 吴磊, 等. 高精度光纤陀螺振动误差抑制技术[J]. 红外与激光工程, 2011, 40(11):2201-2206.DOI:10.3969/j.issn.1007-2276.2011.11.026.

ShuJiantao,LiXuyou,WuLei,etal.Vibrationerrorrestraintechnologyforhigh-precisionfiberopticgyroscope[J]. Infrared and Laser Engineering, 2011, 40(11):2201-2206.DOI:10.3969/j.issn.1007-2276.2011.11.026.(inChinese)

[4]申冲, 陈熙源. 基于提升小波与灰色神经网络的光纤陀螺振动误差建模[J]. 中国惯性技术学报, 2011, 19(5):611-614,620.

ShenChong,ChenXiyuan.Vibrationerrormodelingoffogbasedonliftingwaveletandgreyneuralnetwork[J]. Journal of Chinese Inertial Technology, 2011, 19(5):611-614,620.(inChinese)

[5]TianY,MaJ,LuC,etal.RollingbearingfaultdiagnosisundervariableconditionsusingLMD-SVDandextremelearningmachine[J]. Mechanism and Machine Theory, 2015, 90:175-186.DOI:10.1016/j.mechmachtheory.2015.03.014.

[6]YangY,ChengJ,ZhangK.Anensemblelocalmeansdecompositionmethodanditsapplicationtolocalrub-impactfaultdiagnosisoftherotorsystems[J]. Measurement, 2012, 45(3):561-570.DOI:10.1016/j.measurement.2011.10.010.

[7]DongS,SunD,TangB,etal.AfaultdiagnosismethodforrotatingmachinerybasedonPCAandMorletkernelSVM[J]. Mathematical Problems in Engineering, 2014, 2014:1-8.DOI:10.1155/2014/293878.

[8]陈斌,陆从德,刘光鼎. 基于核主成分分析的时间域航空电磁去噪方法[J]. 地球物理学报,2014,57(1):295-302.

ChenBin,LuCongde,LiuGuangding.Adenoisingmethodbasedonkernelprincipalcomponentanalysisforairbornetimedomainelectromagneticdata[J].China Journal of Geophysics,2014,57(1):295-302. (inChinese)

[9]ŽvokeljM,ZupanS,PrebilI.Non-linearmultivariateandmultiscalemonitoringandsignaldenoisingstrategyusingkernelprincipalcomponentanalysiscombinedwithensembleempiricalmodedecompositionmethod[J]. Mechanical Systems and Signal Processing, 2011, 25(7):2631-2653.DOI:10.1016/j.ymssp.2011.03.002.

[10]ZhangYonggang,GaoZhongxing,WangGuochen,etal.Modelingandsimulationofthesecondfeedbackloopforfiberopticgyroscope[C]//5th International Symposium on Photoelectronic Detection and Imaging 2013: Fiber Optic Sensors and Optical Coherence.Beijing,China, 2013: 89140E1-89140E7.

Vibrationnoiseprocessingmethodfordigitalclosed-loopfiberopticgyroscope

SongRuiChenXiyuan

(SchoolofInstrumentScienceandEngineering,SoutheastUniversity,Nanjing210096,China) (KeyLaboratoryofMicro-InertialInstrumentandAdvancedNavigationTechnologyofMinistryofEducation,SoutheastUniversity,Nanjing210096,China)

Abstract:To solve the problem that the digital closed-loop fiber optic gyroscope (FOG) is easily affected by environmental factors such as shock, vibration and so on in practical engineering applications, the vibration noise model for the FOG signal is established based on the analysis of the output signal characteristics under the influence of vibration and the study of the effects of vibration on the stresses in the fiber coil and the additional phase in the signal. First, a modified local mean decomposition (LMD) method with self-adaptive ability is introduced to decompose the signal to a series of harmonic waves according to the frequencies. Secondly, the kernel principal component analysis (KPCA) method is used to separate the valid signal which reflects the vibration effects from noise. Then, the signal with the eliminated vibration errors is obtained after reconstruction. The vibration characteristics of the FOG in the vehicle-mounted and airborne environments are studied by the line vibration experiments, and ten groups of vibration experimental data are collected and analyzed. The results show that the error coefficients including the quantization noise and the bias instability in Allan variance analysis results of the signal after processing decrease by about 50%, thus improving effectively the output accuracy of the FOG in vibration environment.

Key words:fiber optic gyroscope; vibration error; kernel principle component analysis

DOI:10.3969/j.issn.1001-0505.2016.03.006

收稿日期:2015-11-25.

作者简介:宋锐(1991—),男,博士生;陈熙源(联系人),男,博士,教授,博士生导师,chxiyuan@seu.edu.cn.

基金项目:国家自然科学基金资助项目(51375087)、中央高校基本科研业务费专项资金资助项目、江苏省普通高校研究生科研创新计划资助项目(KYLX15_0138)、东南大学优秀博士学位论文培育基金资助项目(YBJJ1636).

中图分类号:V241.5

文献标志码:A

文章编号:1001-0505(2016)03-0489-05

引用本文: 宋锐，陈熙源.数字闭环光纤陀螺振动噪声处理方法[J].东南大学学报(自然科学版),2016,46(3):489-493.DOI:10.3969/j.issn.1001-0505.2016.03.006.