天津10,m深粉质粘土释水模型试验研究
刘文浩,张淑朝
(天津城建大学土木工程学院 天津300384)
天津10,m深粉质粘土释水模型试验研究
刘文浩,张淑朝
(天津城建大学土木工程学院 天津300384)
土的给水度是基坑工程降水设计的基本参数,其精度直接影响着基坑降水量、降水井的数量和降水时间等的计算。取天津市埋深 10,m的粉质粘土为代表性土样,经室内两次模型槽释水试验,揭示了含水层释水过程和给水度变化过程的内在机理,得出过程给水度与释水时间存在着双曲线的变化规律,进而推出过程给水度与释水时间的关系式,可为今后天津市的基坑降水设计及施工提供一定的参考。
给水度 基坑降水 释水时间 粉质粘土
饱和土在重力作用下通过自由流出方式排出水分的能力一般常称为土的释水性。从单位体积的饱和土中可以释放出来的水的体积称为土的给水度,[1]是表征土释水性的主要指标,是地下水资源评价中最主要的参数。
为准确测定给水度值,国内外学者进行了大量实验。刘俊民等[2]以原状黄土为研究对象进行了室内饱水、释水试验,得出过程给水度与释水时间呈双曲线关系变化,且过程给水度随释水时间的延长而增大,当时间无穷大时得到的给水度才是理论上的真正给水度等结论。张蔚榛等[3]提出无论土壤的质地如何,水位下降时给水度的数值都随水位降深的加大而增大,以及在降深相等的情况下,水位下降速度越来越大的结论。Nachabe[4]提出了水位在浅埋深情况下,排水过程中给水度随时间和水位埋深变化的公式。Said等[5]等提出了在水位浅埋深情况下,用土壤水分探针对土壤剖面水分进行连续监测来估算积水度的方法。王玉红等[6]通过风积砂的室内排水实验,研究了浅层地下水给水度与水位埋深的关系,并用不同的公式计算给水度。赵延风等[7]用介质和渗透液的物理性质指标来表述给水度计算公式。刘学军等[8]在给水度测定方法研究中用原状土筒测法,在室内进行安装、充水并模拟地下水位变化,进行释水试验。在测得不同地下水位降幅时的释水量后,推求给水度。前期研究主要基于土壤学和水文地质学角度,很少从基坑降水的角度去考虑给水度对基坑降水的影响。
本文以天津市埋深为10,m的灰色粉质粘土为代表性土样,开展室内模型降水试验,模拟基坑降水土体释水的真实状态,得到的过程给水度和最终给水度可以为基坑降水设计和施工过程控制提供一定的参考。
1 试验简介
1.1 试验装置
为有效测出土样过程给水度与释水时间之间的关系,设计了试验装置(见图1),采取试验装置四周夹层注水的方式使土样饱水,通过观察侧面开孔的PVC管中水位高度与模型箱周围水体高度的关系来判定土体的饱水情况。饱水时,夹层中的水通过内夹壁的小孔渗入土层,待土层充分饱水后进行释水。释水过程排出模型箱的外围水和监测管中的水,即使土层中的水在重力作用下由通水孔流出。
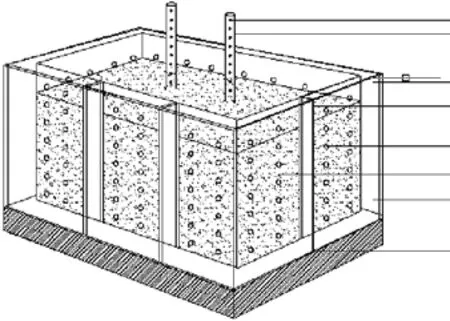
图1 试验模型装置Fig.1 Test model
1.2 试验过程
取天津市地铁6号线宜宾里站10,m深灰色粉质粘土作为土样,土样基本物理性质见表1。

表1 土样物理性质Tab.1 Physical properties of the soil
首先,将取回土样风干后过 2,mm筛,均匀密实地填入实验槽,然后将土样进行饱水,即将水注入到装置四周的夹层,水经通水孔渗入到土层中,当夹层与监测管中的水位达到一致后,取不同深度的土样,采取烘干法进行测定,当不同土样含水率误差不超过±0.2%,[2]时,则认定土层饱水完成。然后打开测定装置下方的水龙头,同时使用水管在 30,s内将模型箱中的外围水和监测管中的水全部排出,开始进行释水试验。试验开始时,每隔 2,h观察夹层和监测管中水位上升的高度,进而得出在这一时间段内土层在重力作用下排出的水的体积。随着排水时间的延续,土层的释水速度会逐步减缓,观察时间的间隔也相应拉长。直至夹层中和监测管中水位高度相同,且高度不再增加时,认为释水阶段结束。
为确保最终数据的可靠性,同时采用烘干法对上述试验进行校核,以保证数据的可靠性。为减小水分蒸发对试验结果的影响,在试验装置上附一层塑料薄膜。
2 原始试验数据整理
2.1 试验原理
给水度 u是单位土体在重力作用下所能排出水的体积占土体体积的体积份额,其计算公式为:

式中:VW——土体所排出水的体积;A——含水层的面积;Δ——土层上表面距离水面的高度。
为校核给水度的准确性,给水度u还可与过程含水率差Δw相互验证。过程含水率差Δw可由下式计算[9]得到:

式中:Wn——饱和土层的含水率;Wt——土层过程含水率,即某个任意时刻的含水率。
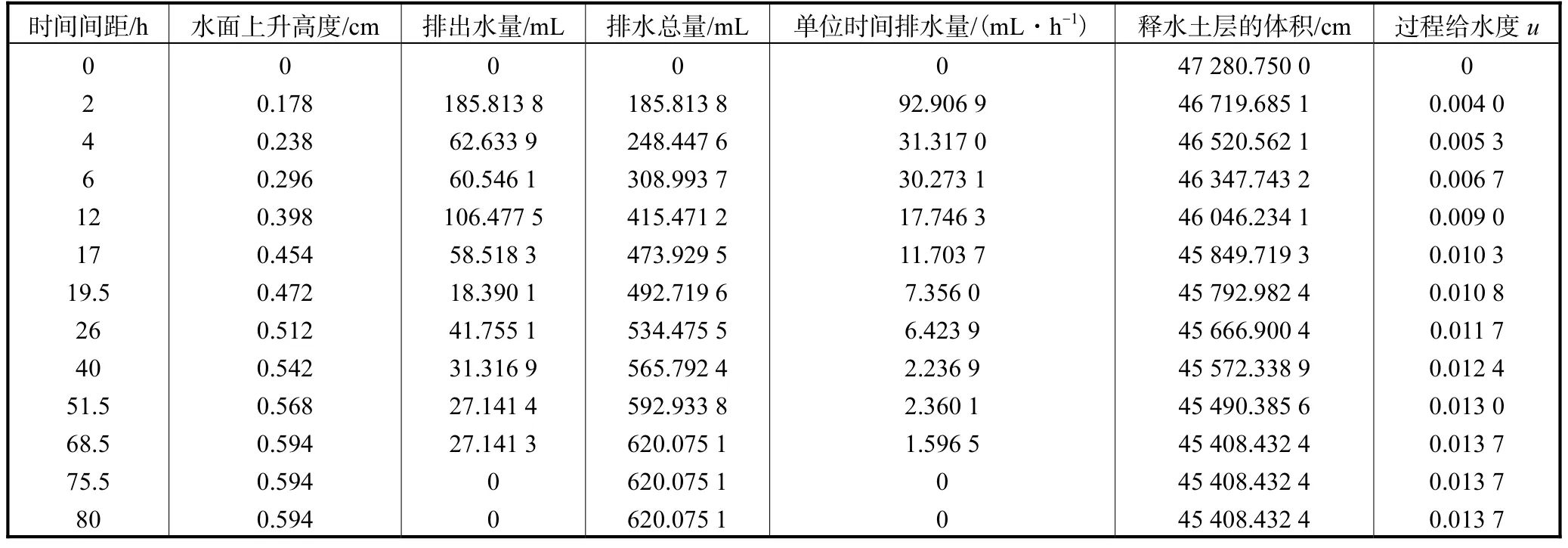
表2 释水时间与过程给水度的关系Tab.2 Relationship between release time and process specific yield
2.2 试验数据
将取得的试验数据填入表2、表3中,表2为释水时间与过程给水度的关系表,且根据式(1)算出过程给水度。
表3 为释水时间与过程含水率之间的关系表,且根据(2)式算出过程含水率差。
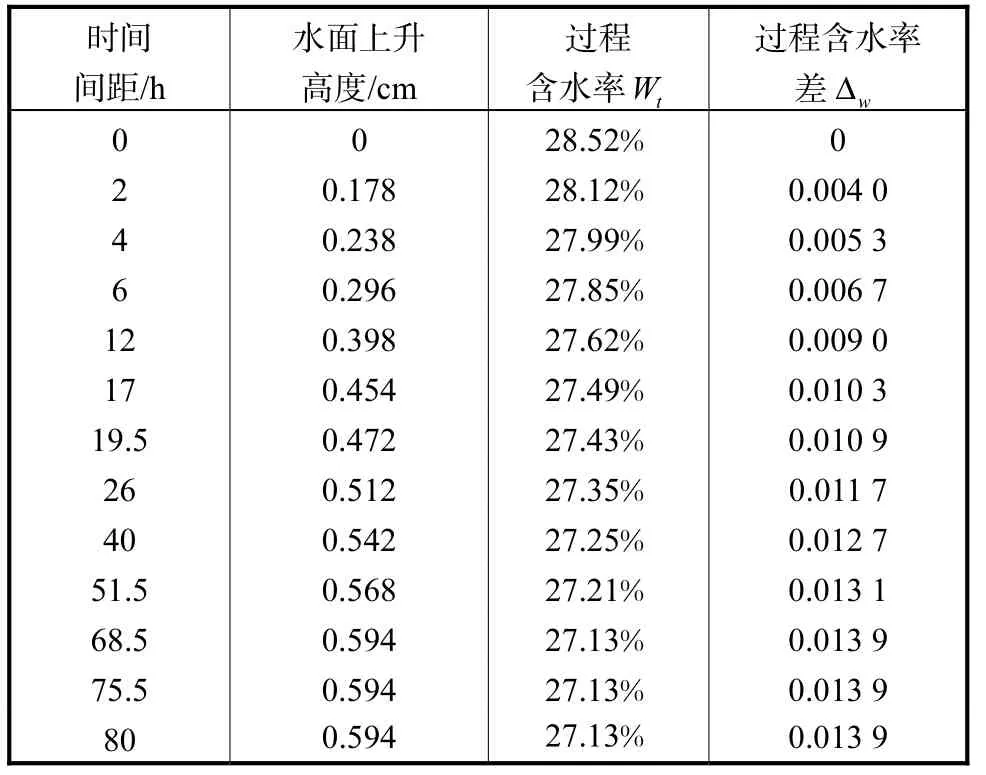
表3 释水时间与过程含水率的关系Tab.3 Relationship between release time and process moisture content
3 试验结果分析
3.1 土层排出水量与释水时间关系
试验取得的排水量和释水时间关系如图2所示,结合表2中所得出的数据可知,单位时间内的排出水量随着时间的增加而减小。而累计排水量随时间不断的累计而不断增加,且增长幅度随释水时间的累计而不断减小,26,h前增长迅速,达到总排出水量的86%,;大致68.5,h时,排出水量达到稳定值。
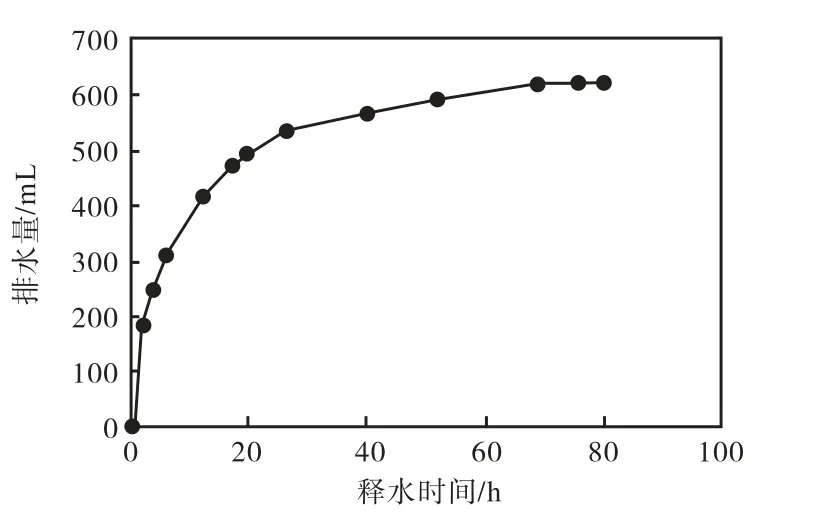
图2 排水量与释水时间的关系曲线Fig.2 Relationship curve between discharged water and release time
3.2 过程含水率与释水时间关系
试验取得的含水率和释水时间关系如图3所示,结合表3中所得出的数据和图2可知,含水率随着时间的增加而减小,且变化幅度随着时间的增加而逐渐减小,26,h前降速很快,26,h后降速趋缓。
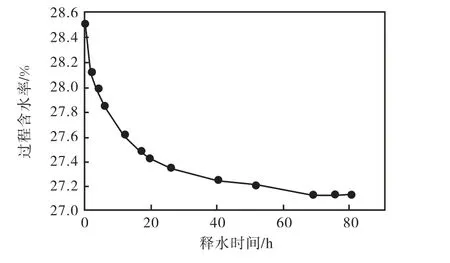
图3 过程含水率与释水时间的关系曲线Fig.3 Relationship curve between process moisture content and release time
3.3 过程给水度与释水时间关系
试验取得的过程给水度和释水时间关系如图 4所示,结合表 2中数据可知,给水度随着释水时间的不断累积逐渐增大,26,h前增长迅速,随后变化幅度随时间延续趋于平缓,68.5,h时给水度不再变化,最终给水度稳定为0.013,7。这与释水时间与排水总量、过程含水率的关系大致吻合,且由两种方法算出的最终给水度分别为0.013,7和0.013,9,仅相差0.000,2,近似视为一致。
以上分析表明,基坑降水施工过程中,26,h内土层释水速度较快,释水量大,需安排较多的水泵抽水,后期随着排水量变化可适当减少水泵数量,3,d后要随时观测抽水井内水位,防止抽干水后水泵空转而损坏。
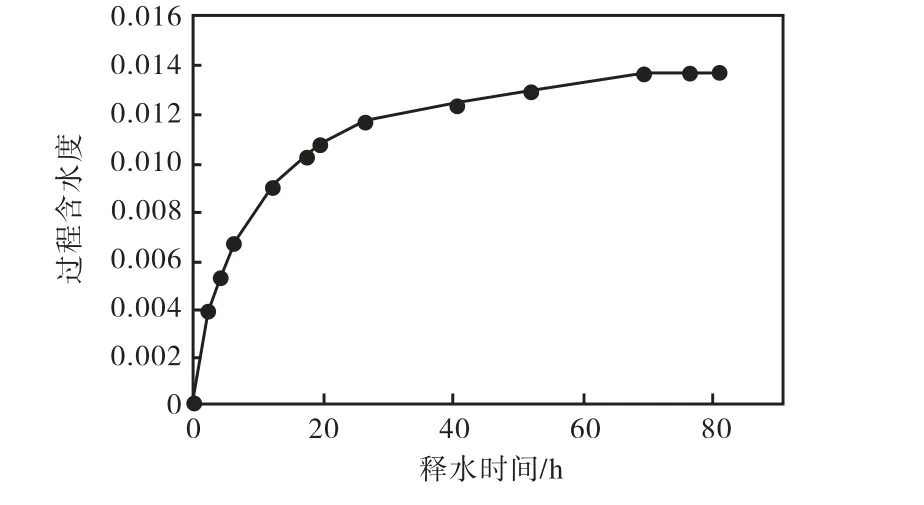
图4 过程给水度与释水时间的关系曲线Fig.4 Relationship curve between process specific yield content and release time
3.4 经验公式的建立
当时间趋向于无穷大时,排出水量趋向于零,由给水度定义可知,给水度也趋向于一个稳定值。由李佩成[6]教授提出的给水度u值与释水时间t呈双曲线关系变化,其表达式为:
u=t/(a+bt)
所以,只要确定a、b值,则可得到给水度与释水时间的关系式。
由试验所得数据可以得出 a=562,b=64.8,结合本次试验可得给水度u与释水时间t的关系为:

由表 4可知,当时间趋向于无穷大时,给水度值u=t/64.8,t,u=0.015,4,与试验最终给水度值相差0.001,7。所以最终得出的 u=t/(562+64.8,t)关系式能较好地反映天津市10,m深粉质粘土的给水度随释水时间的变化规律。
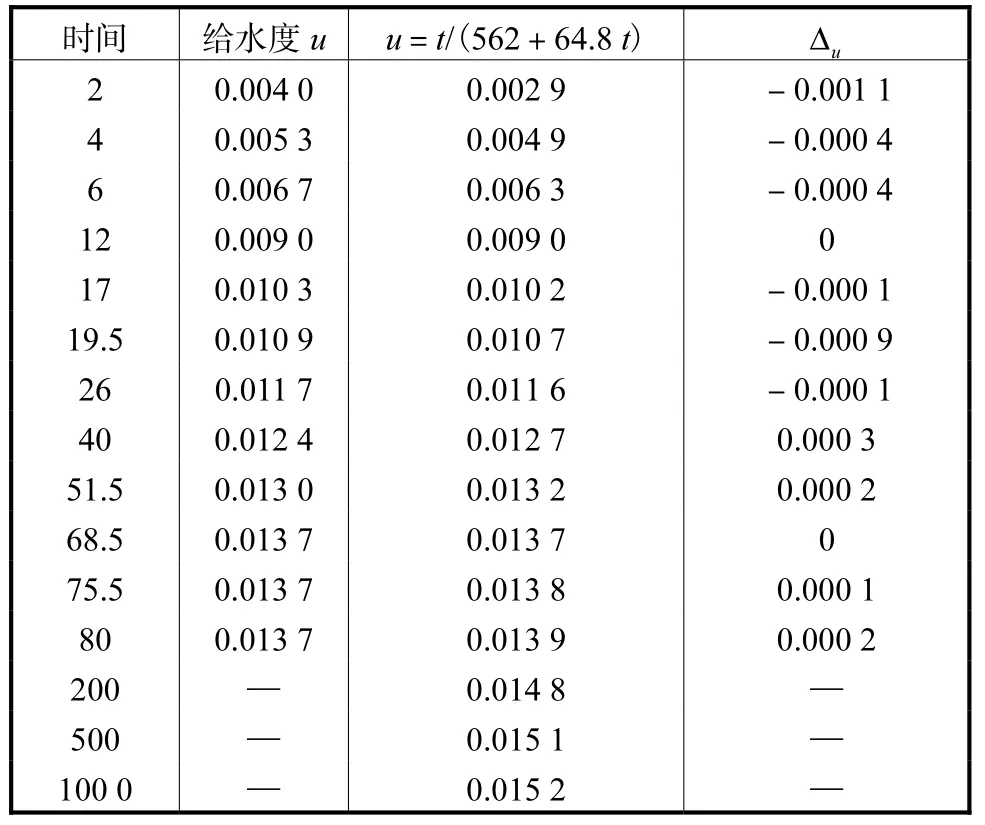
表4 由式(3)算出的给水度值与真实给水度值对比Tab.4 A comparison between the specific yield value and the real value of specific yield by formula(3)
4 结 论
①通过试验得出,降水过程中天津市 10,m深灰色粉质粘土的过程给水度随着时间的增加而增大,26,h前增长迅速,随后增长幅度随着时间的增加而逐渐减小,68.5,h时给水度不再变化,最终给水度值为0.013,7。②天津市 10,m深灰色粉质粘土给水度与释水时间呈现双曲线的关系,并可用关系式 u=t/(a+bt)表示给水度与释水时间二者的关系。当 a=562,b=64.8时,关系式 u=t/(562+64.8,t)能较好地反映该土层的给水度与释水时间之间的关系。③通过过程给水度,可准确计算不同时间段的基坑降水量,合理安排工期,精确控制基坑降水施工过程。④受时间限制,本文只对 10,m深粉质粘土进行了实验研究,要想为天津市基坑降水工程提供整体参考,还需对基坑降水深度范围内的多层土进行进一步研究。■
[1] 邹立芝,杨昌,兵侯杰. 关于给水度的定义[J]. 水文地质工程地质,1994(1):31-33.
[2] 刘俊民,杨平,陈艳霞. 黄土新含水层释水过程和给水度试验研究[J]. 人民黄河,2007,29(3):18-20.
[3] 张蔚榛,蔡美娟. 均质土壤给水度的空间试验和数值模拟[J]. 武汉水利电力学院学报,1988(2):1-11.
[4] Nachabe M H. Analytical expressions for transient specific yiele and shallow water table drainage [J]. Water Resources Research,2002,38(10):1193-1198.
[5] Said A,Nachabe M,Ross M,et al. Methodology for estimating specific yield in shallow water environment using continuous soil moisture data [J]. Journal of Irrigation and Drainage Engineering,2005,131(6):533-538.
[6] 王玉红,程东会,段吉波. 浅层地下水给水度与水位埋深关系的试验研究[J]. 人民长江,2013,45(5):60-65.
[7] 赵延风,王正中,刘计良. 给水度测定仪设计[J]. 农业机械学报,2011,42(9):69-72.
[8] 刘学军,扬维仁. 给水度测定方法研究[J]. 地下水,2003,25(4):221-229.
[9] 李佩成. 给水度合理取值的研究[J]. 地下水,2000(22):21-44.
[10] 李佩成. 黄土含水层给水度合理取值的研究[J]. 水利学报,1999(11):38-41.
A Model Test of the Water Release of 10 m Deep Silty Clay in Tianjin
LIU Wenhao,ZHANG Shuchao
(School of Civil Engineering,Tianjin Chengjian University,Tianjin 300384,China)
Specific yield of soil is the basic parameter for the engineering design of foundation pit precipitation. Its precision directly affects the calculation of foundation pit precipitation, precipitation well number and precipitation time etc. In this paper, silty clay in Tianjin, with a depth of 10 m was taken as a representative sample to carry out water releasing tests for two times. According to test results, internal mechanics of the water releasing process and the change of specific yield of aquifer were shown, namely, the relationship between specific yield and water releasing time is hyperbolic type. Then, the formula indicating the relationship between the two was obtained, which can be used as a reference to foundation pit dewatering design and construction in Tianjin.
specific yield;foundation pit precipitation;water release time;silty clay
TU46+3
A
1006-8945(2016)02-0039-04
大学生创新创业训练计划项目——天津地铁工程减压降水对周边环境的影响分析(201410792025)。
2016-01-15

