冲击噪声背景下独立信号与相干信号并存的测向自适应新方法

刁鸣，刘磊,2，安春莲(.哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨，5000; 2.泰山学院 物理与电子工程学院，山东 泰安，27000)



冲击噪声背景下独立信号与相干信号并存的测向自适应新方法

刁鸣1，刘磊1,2，安春莲1
(1.哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨，150001; 2.泰山学院 物理与电子工程学院，山东 泰安，271000)

摘要：根据冲击噪声的幅值特点和快拍数数量，通过对阵列接收数据进行去冲击预处理后进行数据重构，提出一种冲击噪声背景下独立信号与相干信号并存的 DOA 估计的新自适应方法。首先，估计出阵列接收数据中信号成分的幅值上限；然后，对阵列接收数据中受到冲击噪声影响的数据进行归一化处理，削弱冲击噪声；最后，根据快拍数量对噪声残差数据进行采样后重构信号，利用传统的二阶统计量方法分别对独立信号和相干信号进行达波方向(DOA)估计。研究结果表明：该方法阵列利用率较高，估计性能好，且在强冲击噪声环境和小快拍数下仍然具有良好的估计性能。

关键词：DOA估计；冲击噪声；独立信号；相干信号；二阶统计量；分数低阶统计量

波达方向(direction of arrival,DOA)估计一直是雷达阵列信号处理领域的研究热点，广泛应用于军事和民用[1−2]。传统的DOA估计算法一般假设信号的背景噪声是符合高斯分布的，但随着时间和环境的变化，当今很多实际应用环境中的噪声并不一定完全符合高斯特性分布，往往具有一定的冲击特性，即为冲击噪声。由于冲击噪声信号本身特性决定了其不具备二阶及以上的统计量，因此，传统的基于二阶或高阶统计量的DOA估计方法在冲击噪声背景下失效。为了解决这一问题，人们提出了基于分数低阶统计量方法[3−7]，如分数低阶矩(fractional lower order moment，FLOM)方法[5]、共变系数矩阵(robustCo-variation，ROC)法[6]以及分数低阶协方差(fractional lower orderCovariance，FLOC)方法[7]等。但上述方法都需要事先估计合适的分数低阶参数 p，计算较复杂且不同的参数 p 会产生不同的估计结果。随着电磁环境的日益复杂化尤其是在电子战环境下，捕捉到足够的快拍数越来越难[8]，而且现有算法一般要有数量足够多的快拍数才能保证其测向精度。为此，本文作者利用门限处理思想[9−10]，通过对阵列接收数据进行去冲击预处理，根据快拍数量，利用 bootstrap 方法[11−12]对噪声残差数据进行重构，提出一种在冲击噪声背景下的独立信号与相干信号共存的测向自适应新方法。

1数据模型

且

其中：A 为接收信号的阵列流型矩阵，可分解为非相干的 Au和相干的 Ac；a(θi) =[1,ui, L,]T；ui=e−jπcosθi；B=blkdiag{τ1,L ,τK}；τi为第 i 组相干信号的复衰落因子；Sc(t)=[sC1(t),L,scK(t)]T为K组相干信号的生成信源。对于 SαS 分布的随机过程，由于其不存在固定的概率密度函数，故常用特征函数对其进行描述，其特征函数可以表示为

其中：α为特征指数，且 α∈(0,2]，当 α=2 时，表示高斯分布，α取值越小，则 SαS 过程的冲击性越强；ε 为位置参数，它是 SαS 分布概率密度函数在横坐标上的对称点。本文讨论的冲击噪声为标准 SαS 分布，即ε=0，γ=1。

2　基于二阶矩的 DOA 估计

2.1SαS 噪声滤波去冲击预处理

根据 SαS 分布的特性，其幅值较大的位置对应的是少数冲击分量，而在绝大多数没有冲击分量的位置，幅值较小，因此，可通过滤波预处理的方式对接收到的数据进行处理。首先估算所接收的阵列数据的幅值有效上限Bm作为门限值；然后，对所接收的阵列数据中幅值大于门限值的数据进行归一化处理，将其幅值改为Bm，处理后的数据就能有效地消减冲击噪声对其产生的影响。经过以上去冲击滤波预处理的数据可以直接利用经典的基于二阶矩的方法进行 DOA 估算。去冲击预处理的具体方法如下。

1)根据所接收阵列数据 X(t)估计出幅度门限值Bm。设矩阵 X1(t)为 X(t)中各个对应位置的元素值取绝对值后所构成的M×L维矩阵(L表示数据快拍数)。从X1(t)的L列数据中随机选出Q列构成M×Q维数据矩阵G，最后从矩阵G抽取数据产生向量h：

其中：i=1,2,L ,Q。由于矩阵G中数据是从X1(t)中随机产生的，且由冲击信号的特性分布可知其只在极少数位置出现冲击分量，所以，向量h中的元素既含有受噪声影响不大且幅值相对较小的数据，也有可能含有受到冲击分量影响较大的大幅值数据[13]。

2)为了估算幅度门限值 Bm，需要判断 h 中的各个数据元素是否受到冲击噪声分量的影响，根据影响程度对对应幅值进行修改调整，然后由调整后h中的数据估计出门限值 Bm。设 h0为 h 中数据值最小的元素，根据文献[14]整理出具体的估计步骤和计算过程为：

1)对 h 中的元素按从小到大进行排序，并设h1≤ h2≤ L≤hQ。

2)判断元素中最大值与kh0，若最大值大于kh0，则调整为 hQ=qh0(k和q为常数)；

3)若 hQ＜ kh1，则计算h的均值 Bm=mean{h }。

重复步骤1)～3)，直到计算出Bm为止。

在估计Bm的过程中，k和q为可调参数，对于常见的固定信号而言，既可通过实验得到其最优值，也可通过经验来估计设定。其取值为：

其中：c是取值为0到1之间的随机数。

当求得相应的幅度门限Bm后，就可以得到对X(t)进行归一化处理后新的数据阵列Y(t)，其第i行、第j 列(i=1,…,M,j=1,…,L)的元素为

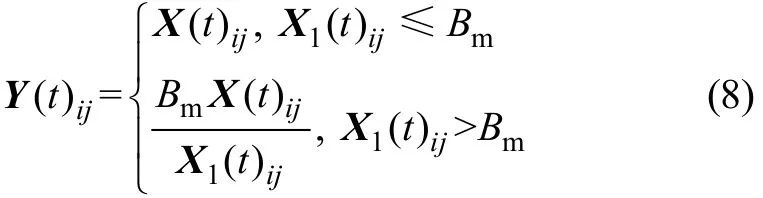
Y(t)可进一步表示为

其中：N1(t)表示被消除冲击后的噪声，其不再具有冲击噪声特性。因此，Y(t)即可采用基于二阶统计量的测向算法进行估计。

2.2小块拍数下的自适应处理方法

由于各种复杂电磁环境的存在，在很多情况下不能顺利获得大快拍数据，所以，利用bootstrap方法重构矩阵来获得满足算法要求的数据。设去冲击预处理后的数据 Y(t)求数据协方差矩阵 R 并进行奇异值分解：

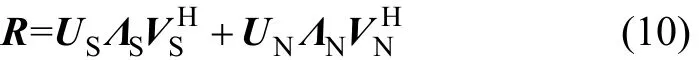
或表达为其中：ΛS和 ΛN分别为较大奇异值和较小奇异值所构成的对角线矩阵；US和 VS分别为大奇异值所表示的左、右2个奇异值矢量矩阵；UN和 VN分别为小奇异值对应的左、右2个奇异值矢量矩阵；RN表示残余噪声的协方差矩阵。根据bootstrap残差法的原则，可对RN进行重采样构成新的后重组矩阵：

为了满足不同条件下采集到的不同数量的快拍数L都能保证有合适的计算量，根据文献[15]对采样数据采用自适应判断的方法：

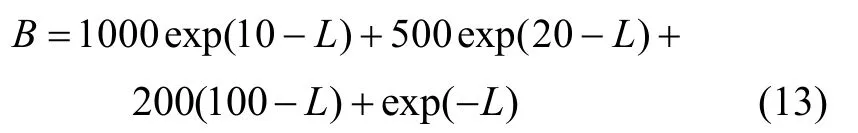
小块拍数数据重构DOA估计方法步骤如下：

1)设接收到的数据矩阵 X=[x(1),L,x(L)]快拍数为L，计算其协方差R；

2)对协方差进行奇异值分解得到US和UN；

3)计算残差数据RN，对其重采样得到，并且重构 R∗；

4)估计样本的特征值，利用 root-music 计算到达角；

5)重复步骤3)和4)B次，得到一系列角度；

6)利用分布函数和置信区间来重新计算角度。

2.3独立信号与相干信号共存的测向新方法

当相干信号和非相干信号同时存在入射信号时，接收数据的协方差矩阵可具体表示为

其中：RSu=E[Su(t)Su(t)H]；RSc=E[Sc(t)Sc(t)H]；RN为残余噪声的协方差矩阵。将R进行奇异值分解得：

其中：较大奇异值个数为 Nu+K 个；较小奇异值个数为 M− Nu− K 个。首先，对独立信号进行DOA估计。利用经典的root-MUSIC算法进行估计：

其中：p(u)=[1LuM −1]T；u=e−jπcosθ。若θ为独立信号对应的角度，则 f(u)=0。由于相干信号的相互干扰，因此，实际上会估算出的根为 Nu+K 个，即包含了 Nu个独立信号对应的根和 K 个相干信号对应的相互干扰。由于相干信号所对应的根比独立信号的对应的根距离单位圆较远，因此，选择距离单位圆较近的Nu对根为独立信号的估计值，其估算公式为

然后，对相干信号进行DOA估计。根据 Ru的结构可知其为 Toeplitz 矩阵，而 Rc不是 Toeplitz 矩阵，因此，利用这一特性，可以分离出相干信号信息：

因为信号子空间与阵列流型所张成的空间为同一空间，所以，必然有1个K维满秩矩阵T满足：

其中：T′=BT，为 Nc×K 维列满秩矩阵。根据压缩感知理论，USc可以表示为

其中：A0=[a (φ1)L a(φD)]，为1个 M×D 维感知矩阵，且D的取值远大于M；φn为对信号的目标空间进行 D 点均匀采样时第 n 次采样所对应的角度；T0为D×K 维行稀疏矩阵，且稀疏度为 Nc。在已知 USc和A0时，利 用稀疏重构算法对T0进行稀疏求解，即 可根据 T0中非零行元素位置获得其在 A0中对应的角度，从而实现相干信号的DOA估计。

3 实验仿真及结果

为了验证所提方法的有效性，本文进行了仿真试验，并采用文献[18]中的MORMP方法进行稀疏求解。由于目前还没有冲击噪声背景下独立信号与相干信号并存的测向算法，故将 RFLOC 方法扩展到独立信号与相干信号并存情况，并与所提方法进行仿真比较。设定估计的信号角度与真实角度的绝对值之差在1°之内时，即可认为估计成功。计算信号角度均方根误差QMSE的公式为

仿真1为了验证所提方法的去冲击噪声能力，取广义信噪比为10 dB。图1所示为特征指数为1.6时去冲击噪声处理效果，其中，图1(a)所示为包含噪声干扰的雷达阵列接收的仿真数据，图1(b)所示为经过滤波预处理去除干扰后的数据。

从图1(a)和图1(b)可以看出：本文所提出的去冲击滤波预处理方法能够有效地去除 SαS 分布中的冲击分量；经过预处理后，原冲击位置处的数据幅度较大幅度降低，能与信号真实幅值相比拟，这表明处理过程有效地平滑了冲击噪声分量，经过处理后的数据已经存在二阶统计量。此外，数据恢复效果随着特征指数的增大而更优。

图1　特征指数为1.6时预处理效果Fig.1　Effects of pre=processing whenCharacteristic index is1.6

仿真2 假设雷达阵列接收到4个窄带远场信号，其中独立信号和相干信号各有 2个。设独立信号的入射角度分别为 30°和120°，相干信号的入射角度分别为25°和65°，特征指数α=1.3。图2所示为本文所提出的方法与 RFLOC 随着广义信噪比变化的估计性能的对比结果。

从图2可以看出：本文所提出的方法无论是对于独立信号还是对于相干信号的估计性能都要比RFLOC方法优越。对于相干信号的DOA估计，本文采用基于压缩感知(CS)的测向方法既不需要进行相干处理，也不降低阵列孔径，有效地提高了算法的估计性能。从图 2(b)可以看出：由于 RFLOC 方法本身的不稳定性，无论对于相干信号还是非相干信号，其估计的均方根误差均比所提方法的大。

仿真3 入射信源的基本参数和仿真2的相同，广义信噪比为10 dB。图3所示为本文所提出的方法的估计性能与 RFLOC 随特征指数α变化的对比曲线。图3中的估计均方根误差计算方法与图2中的一样。

图2估计性能随广义信噪比变化曲线Fig.2Curve of estimated performanceChanged with generalized SNR

从图 3(a)和和图 3(b)可以看出：这2种方法的估计性能随着特征指数逐渐增加均不断提高，但本文所提出的方法的性能依然明显优于RFLOC；在特征指数α小于1时，本文所提出的方法依然具有优良的估计性能；而只有在特征指数α大于1.5时，RFLOC方法才能具有良好的估计性能。故本文所提出的方法在冲击噪声下具有更强的测向能力。

图3　估计性能随α变化曲线Fig.3　Curve of estimated performanceChanged with α

图4不同快拍数下估计成功概率对比Fig.4Probability of successful estimation in different snapshots

仿真4入射信号的结构和角度与仿真2的相同，广义信噪比为5 dB。图4所示为本文所提出的方法与FLOC 方法和 RFLOC 在不同快拍数下的成功概率估计。从图 4可以看出：本文所提出的方法在小快拍数下远优于 FLOC 和 RFLOC 方法；只有在快拍数大于500 时，后2种方法才有较高的估计成功概率。故所提方法能够在小快拍数下依然保持良好的估计性能。

4 结论

1)对阵列接收数据进行去冲击预处理，使得传统的二阶统计量方法可以适用于冲击噪声背景，提出一种新的基于二阶统计量的独立信号与相干信号的测向自适应方法。

2)所提出的方法的估计性能优于传统的分数低阶统计量方法。自适应快拍数算法的引入使得所提算法在小块拍数下依然有着良好的测向性能。所提出的算法将独立信号与相干信号并存的测向算法扩展到冲击噪声背景，进一步提高了测向算法的估计性能。所提出的方法具有适应性强、能抵抗强冲击噪声干扰等优点。

参考文献：

[1]LEONG P H,ABHAYAPALA T D,LAMAHEWA T A.Multiple target localization using wideband echoChirp signals[J].Signal Processing,IEEE Transactions on,2013,61(16): 4077−4089.

[2]DEVENDRA M,MANJUNATHACHARI K.DOA estimation of a system using MUSIC method[C]//RAJU G S N.Signal Processing andCommunication Engineering Systems.Guntur,India: IEEE,2015: 309−313.

[3]HARI K V S,LALITHA V.Subspace-based DOA estimation using fractional lower order statistics[C]//TICHAVSKY P.2011IEEE InternationalConference on Acoustics Speech and Signal Processing Proceedings.Prague,Czech Republic: IEEE,2011: 2580−2583.

[4]ZHAO Xiaoou,LI Li,JING Xiaojun.A fast direction-of-arrival estimation based on the fractional lowerCyclicCorrelation[C]//GUO Limin.Proceedings of Advance Intelligence and Awareness Internet 2010.Beijing,China: IET,2010: 255−258.

[5]LIMC H,SEE SC M,ZOUBIR A M.Robust adaptive trimming for high-resolution direction finding[J].IEEE Transactions Signal Processing Letters,2009,16(7): 580−583.

[6]PANAGIOTIS T,CHRYSOSTOMOS L N.The robustCovariantion-based MUSIC(ROC-MUSIC)algorithm for bearing estimation in impulsive noise environments[J].IEEE Transactions on Signal Processing,1996,44(7):1623−1633.

[7]高洪元.重构分数低阶协方差的子空间拟合测向算法[J].电波科学学报,2009,44(4): 729−734.GAO Hongyuan,DIAO Ming.Direction finding of signal subspace fitting algorithm based on reconstructed fractional lower orderCovariance[J].Chinese Journal of Radio Science,2009,44(4): 729−734.

[8]ERRASTI-ALCALA B,FERNANDEZ-RECIO R.Metaheuristic approach for single-snapshot 2D-DOA and frequency estimation: Array topologies and performance analysis[J].Antennas and Propagation Magazine,IEEE,2013,55(1): 222−238.

[9]EFRON A J,JEEN H.Detection in impulsive noise based on robust whitening[J].IEEE Transactions on Signal Processing,1994,42(6):1572−1576.

[10]TORIO P,SANCHEZ M G.Using polarization diversity to detect and analyze impulsive noise[J].IEEE ElectromagneticCompatibility Magazine,2012,1(3): 39−45.

[11]EFRON B.Bootstrap methods: another look at the jackknife[J].The Annals of Statistics,1979,7(1):1−26.

[12]FENG Hao,LIU Lutao,WEN Biyang.DOA estimation by bootstrap method[C]//WANG Jun.2012 IEEE fifth InternationalConference on AdvancedComputational Intelligence(ICACI).Nanjing,China: IEEE,2012:1153−1157.

[13]刁鸣,安春莲.冲击噪声背景下的 DOA 估计新方法[J].北京邮电大学学报,2013,36(5): 99−104.DIAO Ming,AnChunlian.A novel DOA estimation method in impulsive noise[J].Journal of Beijing University of Posts and Telecommunications,2013,36(5): 99−104.

[14]安春莲.独立信号与相干信号并存的测向算法研究[D].哈尔滨: 哈尔滨工程大学信息与通信工程学院,2013: 96.ANChunlian,DIAO Ming.Research on direction finding forCoexisted uncorrelated andCoherent sources[D].Harbin: Harbin Engineering University.College of Information andCommunication Engineering,2013: 96.

[15]LIU Lei.Applications of bootstrap in radar signal processing[J].Communications inComputer and Information Science,2015,50(3): 474−479.

[16]BILIK I.SpatialCompressive sensing for direction-of-arrival estimation of multiple sources using dynamic sensor arrays[J].IEEE Transactions on Aerospace and Electronic Systems,2011,47(3):1754−1769.

[17]XU Xu,WEI Xiaohan,YE Zhongfu.DOA estimation based on sparse signal recovery utilizing weighted l1-norm penalty[J].IEEE Signal Processing Letters,2012,19(3):155−158.

[18]TRAPP J A,WRIGHT S J.Computational methods for sparse solution of linear inverse problems[J].Proceedings of IEEE,2010,98(6): 948−958.

(编辑 陈灿华)

DOA estimation for uncorrelated andCoherent signals in impulsive noise

DIAO Ming1,LIU Lei1,2,ANChunlian1
(1.College of Information andCommunication Engineering,Harbin Engineering University,Harbin150001,China; 2.School of Physics and Electronic Engineering,Taishan University,Taian 271000,China)

Abstract:An effective self-adaptive method was proposed to eliminate the impulsive noise.Firstly,a threshold value was set up according to the amplitude feature of the array received data.Then,the amplitude of the array received data,whose amplitude is higher than the threshold value,was modified as the threshold value,and the residual noise was re-sampled to reconstruct the data according to the number of snapshot.Finally,theCommon second-order statistics method was utilized to estimate the directions of arrival(DOAs),and the DOAs of the uncorrelated andCoherent signals were estimated separately.The results show that the proposed method is effective in the presence of strong impulsive noise and fewer snapshots.

Key words:DOA estimation; impulsive noise;Coexisted uncorrelated signals;Coherent signals; second-order moment; fractional lower order statistics

中图分类号：TN911.7

文献标志码：A

文章编号：1672−7207(2016)01−0108−06

DOI:10.11817/j.issn.1672-7207.2016.01.016

收稿日期：2015−01−20；修回日期：2015−03−25

基金项目(Foundation item)：国家自然科学基金资助项目(61571149)；中央高校基本科研业务费专项基金资助项目(HEUCF1508)(Project(61571149)supported by the National Natural Science Foundation ofChina; Project(HEUCF1508)supported by the Fundamental Research Funds for theCentral Universities)

通信作者：刁鸣，教授，博士生导师，从事宽带信号检测、处理与识别研究；E-mail: diaoming@hrbeu.edu.cn