新式复合立管弯曲刚度的研究
徐兴振,刘晓娜,王庆丰
(江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003)
新式复合立管弯曲刚度的研究
徐兴振,刘晓娜,王庆丰
(江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003)
摘要:基于目前使用的深海立管,研究设计了一种新式复合立管,并通过理论推导得出新式复合立管的弯曲刚度计算公式,采用有限元模拟的方法,对该类型立管在弯曲载荷作用下响应进行分析。研究表明,有限元方法较好地模拟了新式复合立管的弯曲动态过程,验证了新式复合立管的弯曲刚度计算公式的正确性。
关键词:复合立管;弯曲刚度;计算公式;有限元法
0引言
随着社会的进步和科技的发展,全世界对石油和天然气的需求日益加剧。百年来的不断开发,使得陆上的油气资源不断的消耗枯竭,人们逐步加强了对海洋油气资源的开发力度。我国拥有世界第5的大陆架面积,石油天然气资源相当丰富,但是海上油气发现率很低,更为严峻的是勘探、开发、生产的水域水深不超过300 m,而南海海域水较深处没有得到很大的开发,反而被其他国家大肆钻探开发,这归结为我国缺少深水油气勘探、开发技术装备,因此深水油气勘探、开发技术装备的研究迫在眉睫。
由于海洋油气开发不管采用哪种浮式体系,立管都是油气开发工程的关键部分[1],因而海洋立管工程一直以来都是石油天然气开发的重点工程。深海立管所处的环境特别复杂,需要具备良好的力学性能,一般单层立管很难达到此标准[2]。复合立管结构形式丰富,力学性能良好,在深海采油领域应用日益广泛[3—4]。本文采用理论推导的方法,得出复合立管的弯曲刚度的计算公式,并利用大型有限元软件ABAQUS对在弯曲载荷下钢带缠绕式复合立管进行数值模拟分析,验证了计算公式的正确性。
1复合立管结构形式及弯曲响应理论推导
1.1复合立管的结构形式
钢带缠绕式深海立管是一种结构复合的新式立管。它以高强度钢带为增强体,以内管为基体,并在安装钢带时施加预紧力,使钢带与内管紧密地连接在一起。复合立管分为4层,第1层为内管,第2层为轴向钢带层,第3层为顺时缠绕钢带层,第4层为逆时缠绕钢带层。逆时缠绕钢带与顺时缠绕钢带的起始角度为45°。每层钢带有40根小钢带组成。复合立管结构形式如图1所示,几何参数见表1。

1.内管 2.轴向钢带层 3.顺时缠绕钢带层
表1复合立管各层几何参数 mm

几何参数第1层内管轴向钢带层螺旋钢带层1螺旋钢带层2内径200230246262厚度15888外径230246262278中面半径107.5119127135宽度18.0619.3220.56
1.2弯曲响应理论推导
复合立管在预紧力的作用下使各层紧密地贴在一起,所以可近似认为各层之间是一种粘结状态,忽略各层之间的相对滑移。复合立管满足平断面假定,而且在同一个立管截面上,不同螺旋钢带层由于弯曲引起的轴向应变不同。某个钢带层的轴向应变εi可用式(1)表示:
εi=kRcos2αsinθi
(1)
式中:R为钢带层的中面半径;α为该螺旋钢带层的螺旋角度;k为弯曲曲率;θi为螺旋钢带层第i根钢带的角度坐标,其计算方法见式(2):
(2)
式中:如图2所示,在坐标系XYZ中,Z沿着轴向方向,X、Y沿径向方向;θi1为某螺旋钢带层其中第i根钢带由于所选截面轴向坐标的变化,导致角坐标引起的变化;θi2为第i根钢带在端部截面处的角度坐标;L为管的总长度。
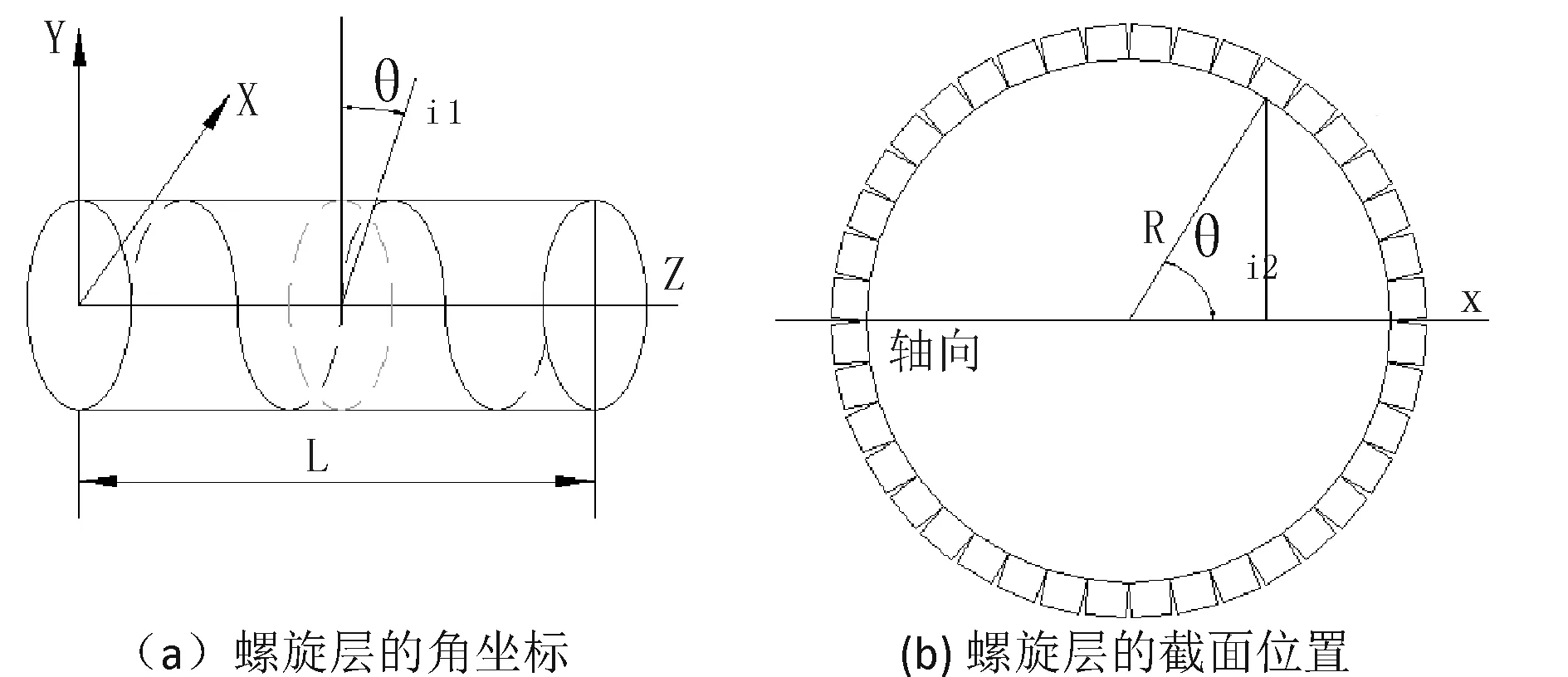
图2 螺旋钢带层结构图
当螺旋钢带层发生轴向应变时,引起的应变能U见式(3):
(3)
式中:E、A分别为钢带层的弹性模量和截面面积;ε为钢带轴向应力;j为第j层钢带层。
由于钢带层具有对称性,其长度和角坐标的关系见式(4):
(4)
式中:s为钢带层长度;θ为在横截面上,钢带层上的点与截面圆心的连线与钢带起始点与截面圆心连线在截面上的投影的夹角。
将式(1)带入式(3),可以得到钢带层的应变能计算公式:
(5)
式中:n为钢带总个数。
外力矩M所做的功W可以表示为:
W=MLk
(6)
根据能量守恒得出外载荷的做功W与钢带层内部产生的应变能U相等,即U=W,联立式(5)和式(6),可以推导出螺旋钢带层外力矩M与弯曲曲率的关系式以及弯曲刚度EI的求解公式如下:
(7)
(8)
根据复合立管的基本参数,计算该复合立管的弯曲刚度。内管的弯曲刚度可由式(9)求得。
(9)
式中:r0为管的外半径;r1为管的内半径。
1.3临界弯矩值的推导
材料处于弹性变形范围时,变形与外力成正比关系。当外力达到一定值时,材料会发生屈服,变形与外力不再成正比关系。在实际的工作中,许多构件不是受单一载荷的作用,而是受多种载荷共同作用。当复合立管受到弯矩的作用时,平衡方程如下:
(10)
M总=M1+M2+M3+M4
(11)
式中:M总为立管所受的总弯矩;M1为内管所承受的弯矩;M2为第1层钢带所承受的弯矩;M3为第1层螺旋钢带所承受的弯矩;M4为第2层螺旋钢带所承受的弯矩。
当复合立管受到拉力的作用时,平衡方程见式(12):
E1εA1+E2εA2+E3εA3cosα+E4εA4cosα=F
(12)
式中:F为立管所受的拉力;A1为内管的截面积;A2为第1层钢带的截面积;A3为第1层螺旋钢带层截面积;A4为第2层螺旋钢带层的截面积。
(13)
σ≤σs
(14)
式中:Fn为第n层所受到的力;σ为距中性轴为y点的应力;σn为轴向力产生的轴向应力;σm为弯矩在距中性轴y处产生的应力;An为管截面积;Mn为第n层分担的弯矩值;y为距中性轴的距离;In为轴向惯性矩;σs为屈服应力。
2复合立管有限元模型的建立
2.1有限元模型
本次计算选用3 m长新式复合立管模型作为研究对象,进行数值仿真研究。内管材料选用强度级别相对较低的可焊管X60,而钢带选用强度级别较高的不可焊接钢材料TC3;建模时内管使用实体单元,钢带使用梁单元。有限元模型如图3所示。材料属性设置见表2。
2.2边界条件
在立管的2个端面中心点处分别建立1个参考点,两端的所有节点与该参考点全自由度耦合如图3(b)所示。表3为具体自由度限制情况。
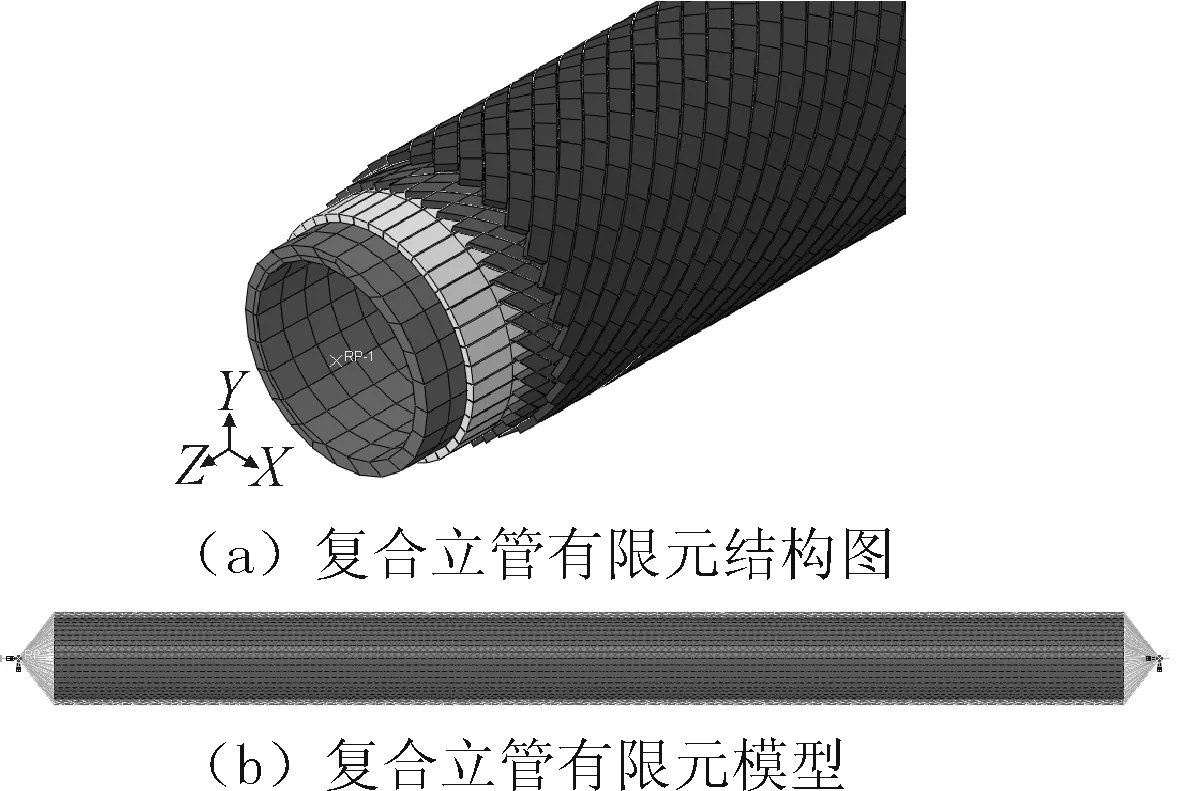
图3 复合立管弯曲响应分析有限元模型

材料名称杨氏模量/MPa泊松比密度/(kg·cm-3)屈服强度/MPaX602070000.37850414TC31180000.3444301000
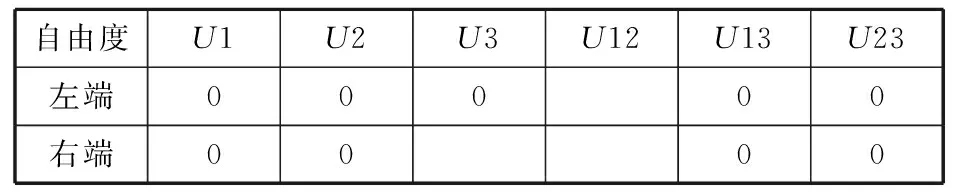
表3 复合立管弯曲载荷作用下模型边界条件
为了减小计算结果的误差,在计算时需加1个轴向的拉力。轴向拉力使各层之间形成良好的相互作用,施加轴向拉力的大小为4 000 kN。在两端施加1个均匀的角速度ω=0.001 rad/s,如图4所示。

图4 复合立管弯曲载荷作用下边界条件示意图
在模型处理上,假设管与钢带以及钢带与钢带之间的接触为理想状态,即立管各层之间没有相对滑动,此时立管的复合刚度最大。计算分析中可以采用无相对滑移条件下的弯曲刚度来描述复合立管的弯曲特性。
3结果对比分析
3.1理论推导计算结果
当立管受到4 000 kN的拉力时,可推导临界弯矩值为:M=2.32×105N·m。
将复合立管的数据带入式(8)与式(9),得出复合立管各层弯曲刚度,具体数值见表4。
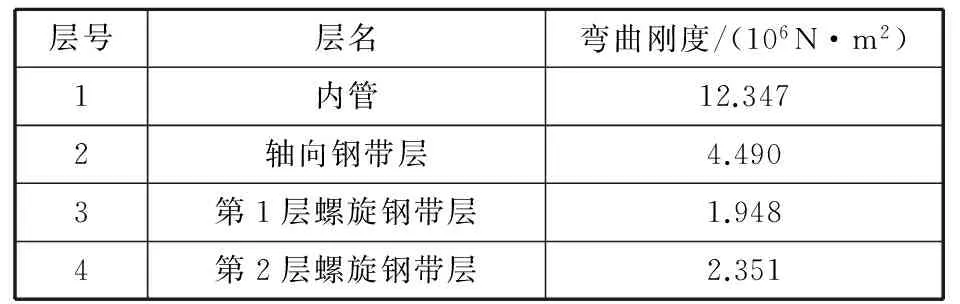
表4 复合立管各层弯曲刚度
通过理论计算,得出复合立管弯矩与弯曲曲率为线性正比例关系,如图5所示。
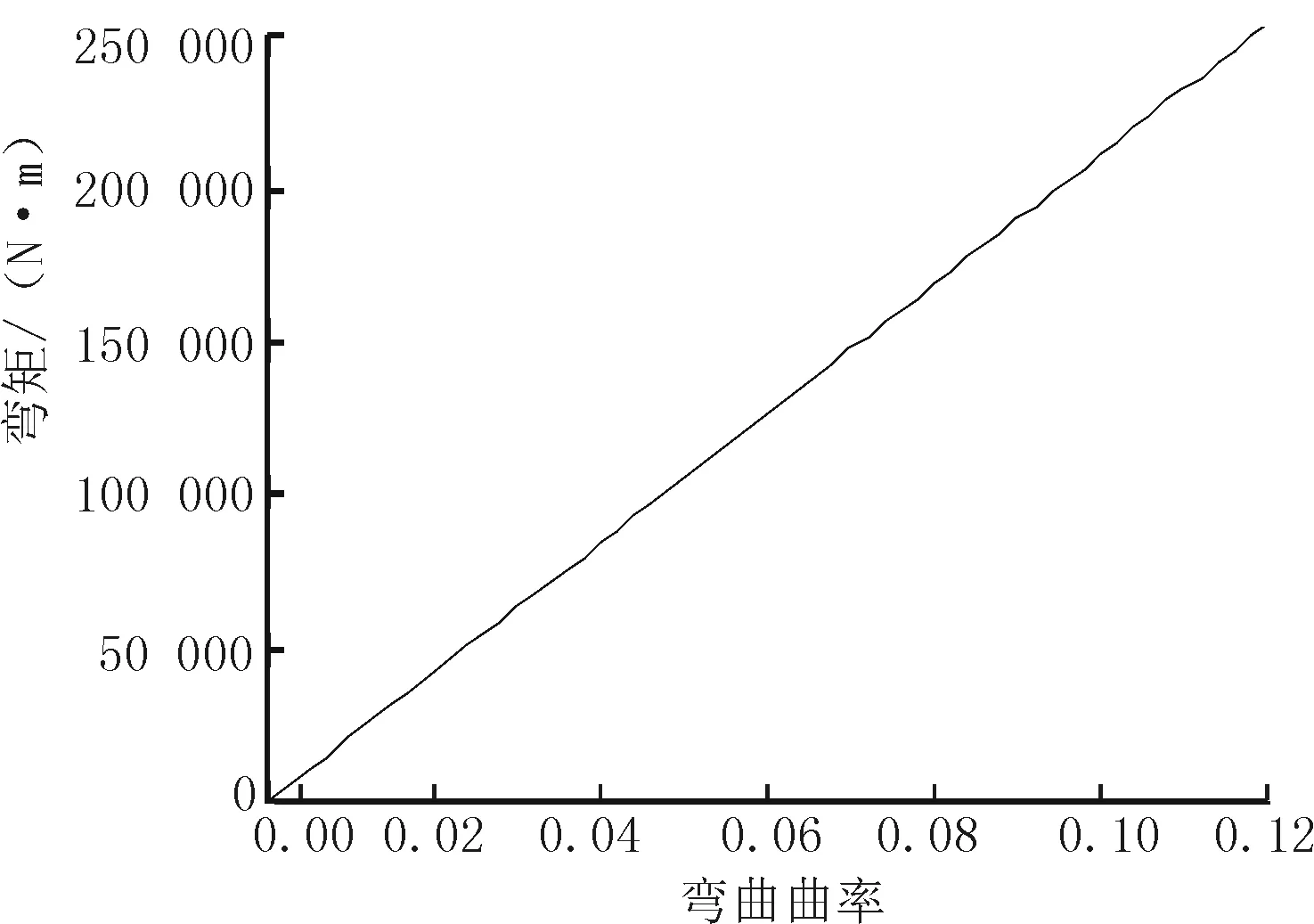
图5 复合立管弯矩与弯曲曲率关系曲线
3.2有限元计算结果
通过有限元计算,得到复合立管弯矩与转角的关系曲线,如图6所示。
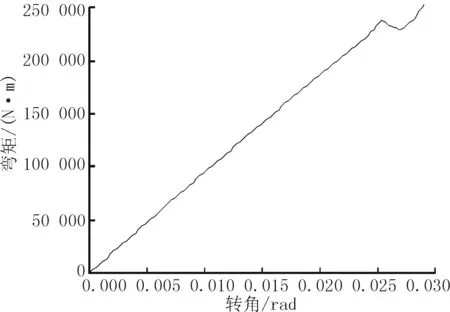
图6 复合立管弯曲载荷与转角的关系曲线
梁的复杂弯曲计算公式:
(15)
(16)
(17)
式中:Φ为管受弯矩变形后,起始点切线与水平方向的夹角;T为轴向拉力;Ψ1(μ)和Ψ2(μ)分别为梁的复杂弯曲辅助函数。
通过计算得出μ值,经查表可知Ψ1(μ)=0.563,Ψ2(μ)=0.32。
(18)
提取有限元计算结果,带入式(13),即可获得复合立管弯矩-弯曲曲率关系曲线,如图7所示。图中曲线的斜率即为复合立管的弯曲刚度。当曲率在0~0.104区间时,曲线的斜率恒定,材料为弹性变形;曲率在0.104~0.120时曲线的斜率出现波动,此时结构材料出现了塑性变形。
3.3有限元计算结果与理论推导对比
将图5的理论计算结果和图7有限元计算结果进行对比如图8所示。通过观察2条曲线发现,材料在弹性阶段有限元计算结果和理论计算结果吻合性较好,理论推导计算得出的新式立管的弯曲刚度与有限元仿真得到的弯曲刚度基本一致。这说明理论推导出的新式复合立管弯曲刚度计算公式在材料弹性变形阶段是正确的。

图7 复合立管弯矩与弯曲曲率关系曲线
4结论
(1)材料在没有发生塑形变形前,复合立管的结构响应基本呈现线性关系。
(2)通过理论公式与有限元结果的对比,显示新式复合立管在弹性阶段的弯曲强度理论推导结果与有限元结果一致,说明理论推导公式能够正确地计算螺旋钢带的弯曲强度。

图8 有限元结果和理论结果的对比
参考文献:
[1]郭宇. 深海立管涡激振动的大涡模拟与涡激疲劳累积损伤分析[D]. 哈尔滨:哈尔滨工业大学,2012.
[2]罗佐县.我国海洋油气生产对外合作现状及展望[J].化学工业,2009(7):23-25.
[3]肖帅. 深水顶张式立管疲劳与裂纹扩展研究[D]. 北京:北京化工大学,2012.
[4]董小林,王法力,邢春雷,等.驳船横荡运动下海洋立管的动力响应[J].海洋湖沼通报,2007(3):143-149.
[5]FeretJJ,BournazelCL.CalculationofStressesandSlipinStructuralLayersofUnbondedFlexiblePipes[J].JournalofOffshoreMechanicsandArcticEngineering,1987,109(3):263-269.
[6]吕莉.海洋立管法兰结构设计与有限元分析[D]. 哈尔滨:哈尔滨工程大学,2008.
收稿日期:2015-10-14
作者简介:徐兴振(1988—),男,硕士研究生,研究方向为船舶结构设计及强度;刘哓娜(1990—),女,硕士研究生,研究方向为船舶结构设计及强度;王庆丰(1976—),男,副教授,硕士生导师,主要研究方向为船舶结构设计及强度、船舶制造工艺力学。
中图分类号:P756.2
文献标志码:A

