圆环形薄板大挠度变形有限元分析比较研究

陈杰平，李　进，乔印虎(安徽科技学院　机械工程学院，安徽　凤阳　233100)



圆环形薄板大挠度变形有限元分析比较研究

陈杰平，李进，乔印虎
(安徽科技学院机械工程学院，安徽凤阳233100)

摘要:环形薄板是汽车减振器中的一个重要零件，属于典型的大挠度非线性变形，传统的计算方法要么产生误差较大，或者计算繁琐不利于工程应用。本文借助于现代分析软件，利用有限元分析方法对汽车减振器中不同规格环形薄板的大挠度变形情况进行了研究。根据von Kármán提出的微分方程，结合钱氏摄动法给出了求解大挠曲变形的解析表达式，拟合出了解析式中的待定系数的数学表达式，并针对固定半径比、内/外径等不同情况进行了计算分析和误差比较。数值计算证明，使用的方法合理可靠，求解精度高、简单快捷实用，误差在3%以下，完全可以满足工程设计分析的需要。

关键词:圆环薄板;大挠度变形;有限元;钱氏摄动法

汽车减振器是汽车悬架中的重要零部件之一，其工作原理是利用活塞和底阀上的阀片式节流阀产生的节流缝隙而产生阻尼减振作用，圆环形阀片的最大挠度变形量直接决定减振器工作性能，影响车辆平顺性和操纵稳定性。减振器阀系设计一直是困扰减振器设计的关键问题［1］。目前，国内、外还没有准确、可靠的设计方法［2－3］，大都是利用经验确定设计参数［4］、经过反复试验和修改来完成设计参数的确定。因此，对环形节流阀片挠曲变形进行高精度计算具有重要意义［5－6］。

由于减振器环形阀片的厚度h远小于半径r，属于环形薄板情况，需要使用弹性力学的薄板理论计算，其挠曲变形主要由基于小挠曲和大挠曲两种理论，针对小挠曲变形的研究已经比较深入和成熟［7－10］。由于按照小挠度弹性变形的方法进行分析计算简单和便捷［11－12］，在工程设计实际应用中得到了广泛应用。但实践证明，减振器环形阀片的工作状况大多都属于大挠度变形，是一个典型的非线性问题，按照小挠曲理论或经验公式［13］计算的挠度值与实际挠度值差异较大，不能满足产品开发和优化设计要求。但环形薄板的大挠度变形的精确解求解较为困难，钱伟长先生提出了钱氏摄动法进行大挠度变形的求解，可以达到很高的精度［14］，但由于其方法的繁琐限制了在工程上应用。

本实验在对环形薄板的挠曲变形进行了认真分析和比较基础上，采用摄动法与有限元数值解法相结合，拟合得到变形解析式来进行环形薄板大挠曲变形设计计算，并对拟合精度进行了验证，探索一种便于工程应用的方法和途径。

1　圆环薄板的挠曲数学模型建立

1.1力学模型

汽车减振器中的环形阀片工作为轴对称结构，可简化为内边缘固定夹紧，在均布压力q作用下外边缘可以自由发生挠曲的力学结构。假设外圆半径为a、内圆半径为b，可建立如图1所示坐标系下的力学模型。

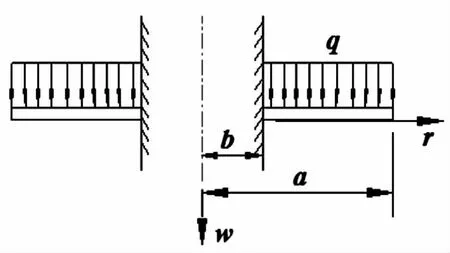
图1　环形阀片的力学模型Fig.1　 Mechanical model of Circular slice－plate

1.2圆环薄板的von Kármán数学模型

针对以上环形阀片轴对称形式的力学模型，1910年von Kármán提出的非线性微分方程表达式如下:

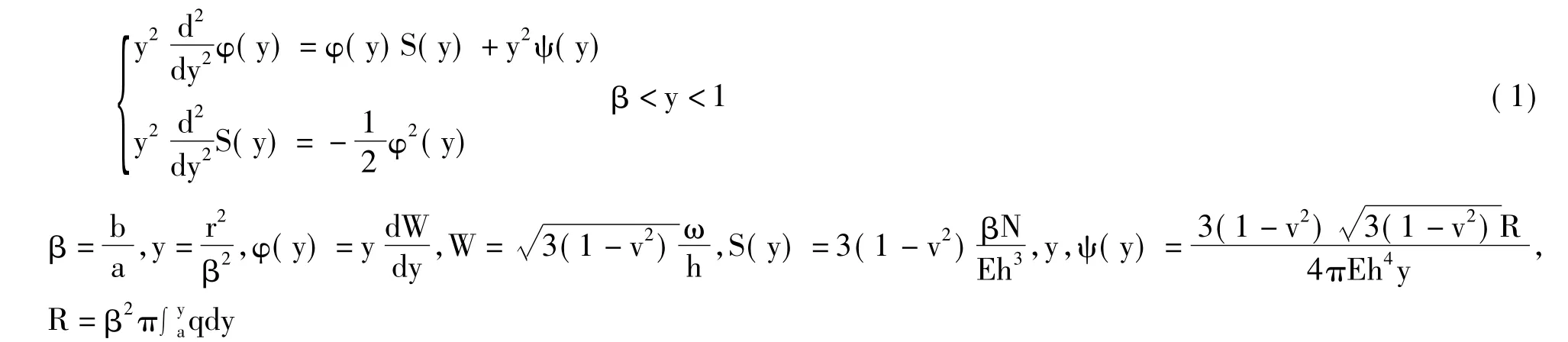
其中: a——圆环薄板外径(mm)

b——圆环薄板内径(mm)

ν——材料的泊松比

E——弹性模量(Pa)

h——圆环薄板的厚度(mm)

w——薄板的挠度(mm)

q——薄板上作用的分布载荷(Pa)

Nr——薄板的径向薄膜张力(N)

r——径向坐标

边界条件为:

1.3大挠曲变形的钱氏摄动解法

钱氏摄动法广泛用于求解各种弹性薄板的大挠曲变形问题，一般取二阶摄动即可获得足够高的精度。取r = a外边缘处的挠度为摄动参数Wm，且有:

根据钱氏摄动法，将所有未知函数展开为Wm的幂级数，即有

将(3)代入(1)、(2)和边界条件中，比较Wm的同次幂系数，从而求解各待定系数，即可得到环形阀片大挠曲刚度曲线方程为

2　Abaqus有限元分析与曲线拟合

由式(4)可知，待定系数λ1、λ2的确定是求解环形阀片挠曲变形关键，但其解析求解依然不便。Abaqus具有很强的非线性分析功能，工程应用中可以采用利用Abaqus进行有限元，然后数值实验结果拟合得到λ1、λ2，进而得到大挠曲变形的解析方程。

2.1有限元分析模型与实验

以某款汽车减振器环形阀片为例，主要参数为a =11 mm，b =5 mm，h =0.3 mm，E =210GPa，υ=0.3，q =1.0Mpa。实际建模中采取Abaqus默认的单位制，即m、N、kg及其导出单位。可建立不同网格密度的环形阀片有限元模型并得到分析结果，如图2和图3所示。

图3　环形阀片有限元分析Fig．3　 Finite Element of Circular thin－plate

在不同网格密度情况下进行有限元分析，可得到圆环薄板边缘处的大挠度变形结果如表1。

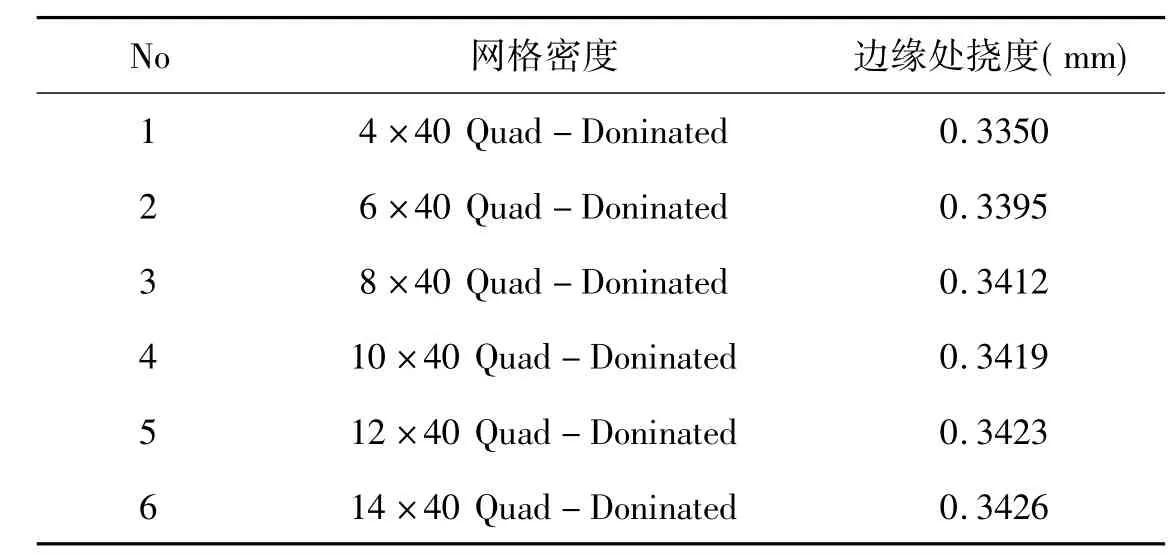
表1　不同网格密度圆环的最大挠曲变形值Table 1　 Maximum deflection value in various grid density rings

将表1按序号和挠度为坐标绘制曲线，如图4所示。可以看出，在序号4(即当周向单元为40、径向单元达到10以上)时，即可得到较高的求解精度。

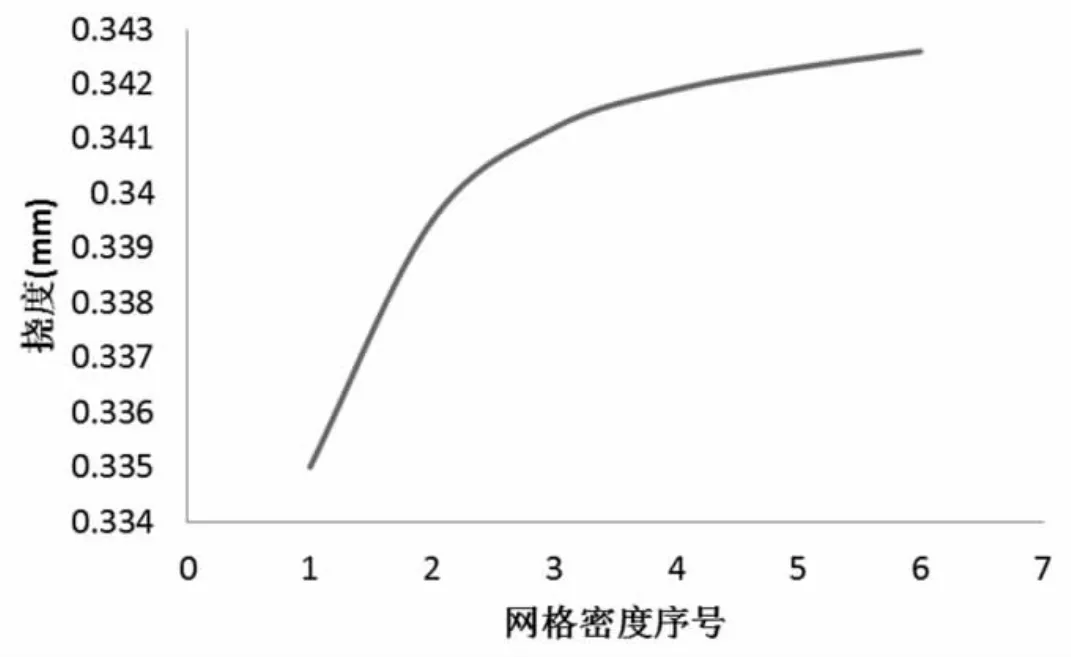
图4　不同网格划分边缘挠度Fig.4　 edge deflection in different mesh

2.2曲线拟合

为进行有限元数值实验，定义β= b/a为环形阀片内外半径之比。考虑到阀片实际几何尺寸及材料特性，令h =0.3 mm，E =210 GPa，υ=0.3，q =1.0MPa。对于轿车减振器来说，环形阀片圆环内圆半径一般为5 ～8mm，外圆半径处于8.5～15之间，即β一般位于0.35～0.75之间。可根据不同的β取值来确定外径，然后按照14×40 Quad－Doninated划分网格，利用有限元分析确定环形阀片外边缘处挠度，如表2。

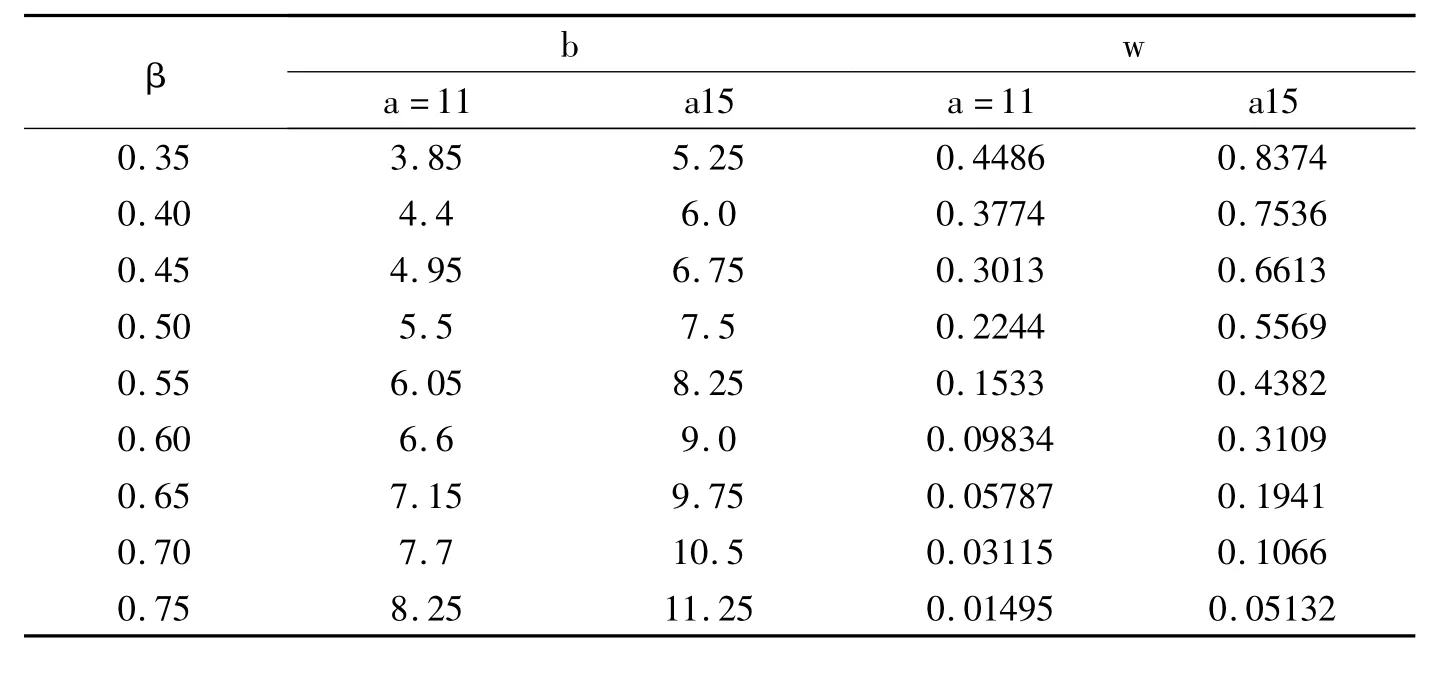
表2　不同内外径比最大挠曲值Table 2 Maximum deflection value in various I/O diameter ratio

将表2中得到的同一β值下的两个挠度值代入式(4)，即可确定待定系数λ1、λ2，见表3。

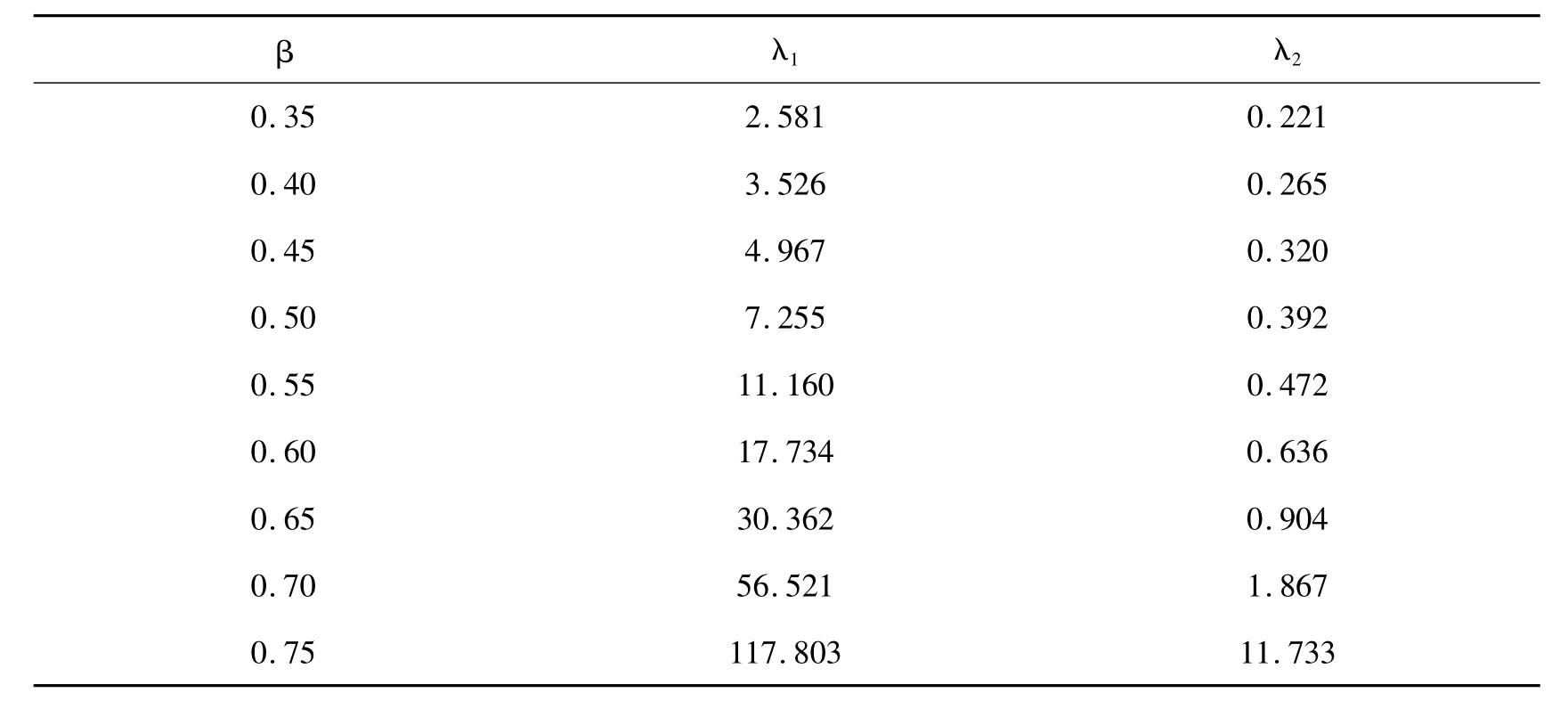
表3　待定系数Table 3 Undetermined coefficient

根据以上得到的待定系数值，可以确定采用Rational待定系数拟合公式分别为:

其中: c1=3.258、c2=－1.054、c1=0.6139、d1=－1.692、d2=0.7206; e1=255.5、e2=－217.9、e3= 157.5、l1=－1176、l2=893.1。

λ1和λ2拟合曲线如下图所示:

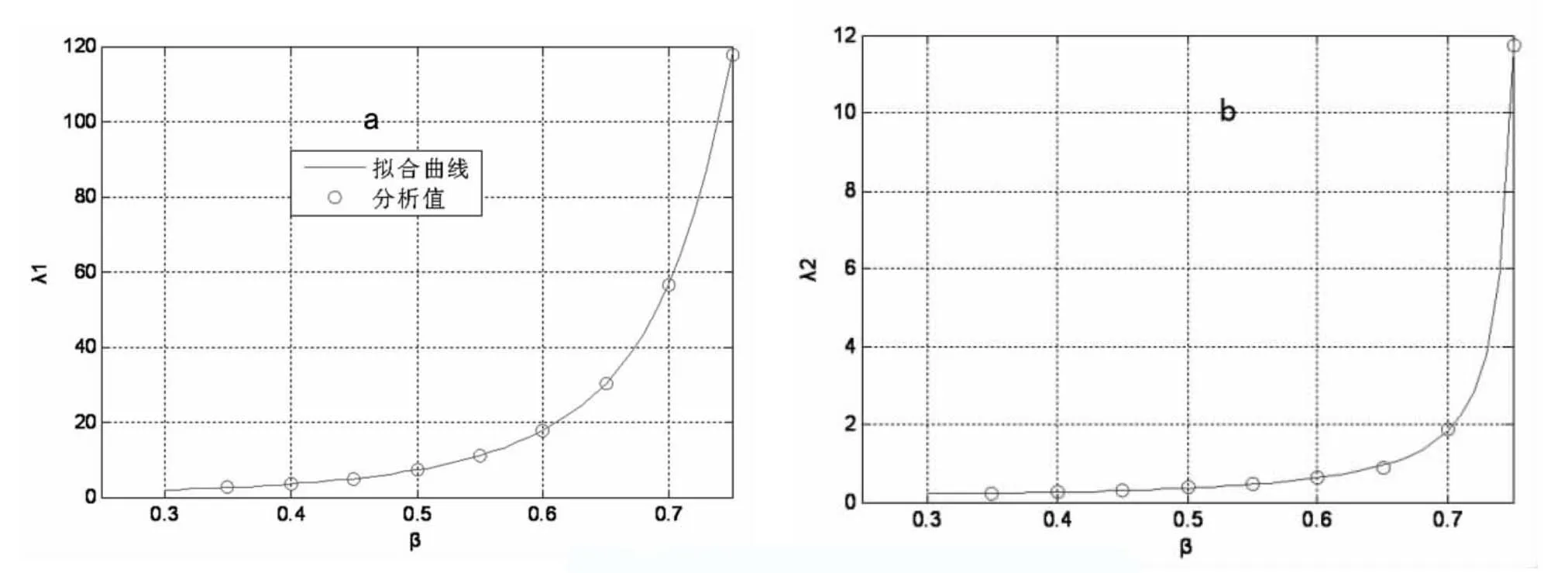
图5 λ1和λ2拟合曲线a.λ1　 b.λ2Fig.5　 Fitting Curve of λ1and λ2

3　验证比较

为验证解析解的正确性，结合前述汽车减振器阀片参数，保持材料特性及薄板厚度h =0.3 mm，E = 210 GPa、υ=0.3、q =1.0 Mpa不变，分别在不同情况下下进行有限元分析并与数值解比较验证。

(1)环形阀片的结构参数及为a =11 mm，b =5 mm，可知其β=0.455。同时改变a、b参数，而保持β不变，利用式(5)可以确定:λ1=5.162和λ2 =0.3105。利用解析式(4)，可以求得的不同a、b时的最大挠曲变形解析解与有限元分析结果，见表4:

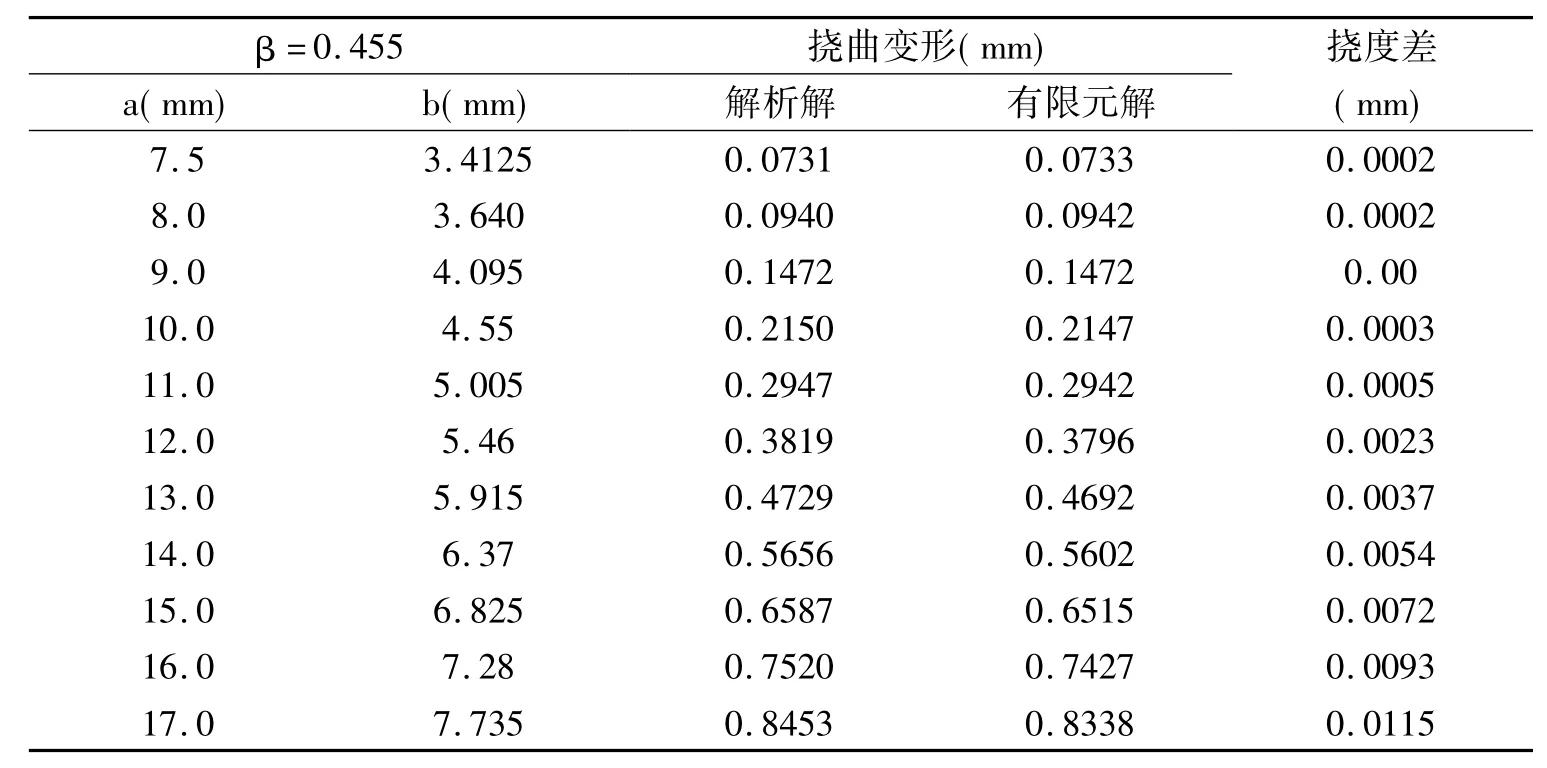
表4　β=0.455不变情况下挠度变形Table 4 The deflection in β=0.455

(2)内径b不变，改变外径a，即β在0.35～0.75之间变化情况下的最大挠曲变形解析解与有限元分析结果，见表5。

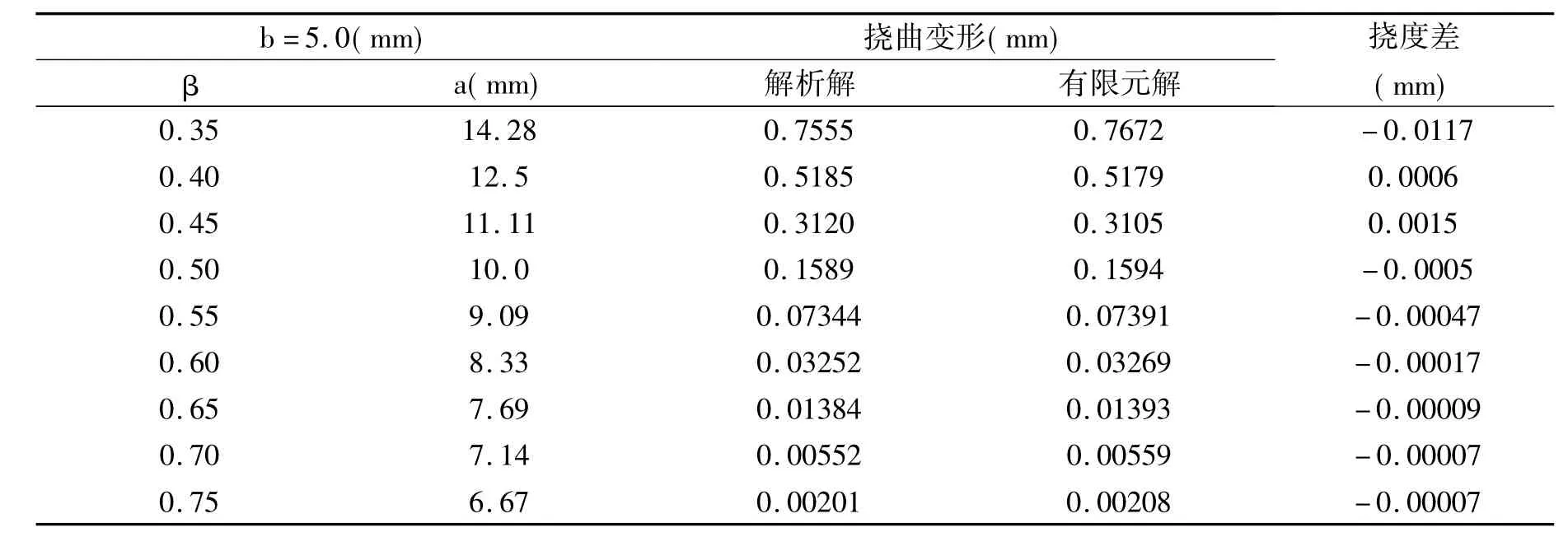
表5　固定内径情况下的挠曲变形Table 5 Flexural deformation of determined inner diameter case

(3)外径a不变，改变内径b，使β在0.35～0.75之间变化情况下的最大挠曲变形解析解与有限元分析结果，见表6。

表6　固定外径情况下的挠曲变形Table 6　 Flexural deformation of determined outer diameter case

通过以上各类情况下的有限元仿真结果与数值计算结果比较可知，两种方法产生的误差在0.02mm以内，具有较高的模拟计算精度。

4　结论与讨论

本实验根据von Kármán微分方程，结合钱氏摄动法推导了减振器环形阀片大挠曲变形的计算方程，利用现代工程软件进行了大量的仿真分析，在进行数值实验的基础上拟合出了环形阀片大挠曲变形的解析计算公式。验证结果表明，该解析式在不同情况下都具有较高的计算精度，产生的误差在3%以下，完全可以满足工程设计的需要。该方法将有限元方法与传统解析计算方法进行了有机结合，使复杂的环形阀片大变形问题求解得到简化。可以证明，所推导的解析式完全不但可以适用于环形阀片大挠度薄板计算，同样也可以适用于环形阀片小挠曲变形的计算，使计算精度得到显著提高。该方法可以为解决汽车减振器节流阀片的设计计算、分析研究、优化设计等工程实际问题提供了新的途径，同时也可用于解决其他领域同类问题。

参考文献:

［1］李世民，吕振华.汽车筒式液阻减振器技术的发展［J］.汽车技术，2001(8) : 10－16.

［2］周长城，顾亮，王丽.节流阀片弯曲变形与变形系数［J］.北京理工大学学报，2006，26(7) : 581－584.

［3］姚嘉伶，蔡伟义，陈宁.汽车半主动悬架系统发展状况［J］.汽车工程，2006，28(3) : 276－280.

［4］陈勇，何辉，白金福.夏利轿车液力减振器簧片的变形分析［J］.汽车技术，2000(1) : 19－20.

［5］Duym S.Simulation tools，modelling and identification，for an automotive shock absorber in the context of vehicle dynamics ［J］.Vehicle System Dynamics，2000，33: 261－285

［6］贺李平，顾亮，辛国国，等.减振器环形阀片大挠曲变形的高精度解析式［J］.北京理工大学学报，2009，29(6) : 510－514.

［7］吕振华，李世民.筒式液阻减振器动态特性模拟分析技术的发展［J］.清华大学学报:自然科学版，2002，42(11) : 1532－1536.

［8］周长城，任传波.最佳阻尼匹配减振器阀片厚度优化设计与特性试验［J］.振动工程学报，2009，22(1) : 54－59.

［9］ZHOU Chang－cheng，ZHENG Zhi－yun，GU Liang，et al.Study on the availability opening size of throttle and affect－tion to the velocity characteristic of shock absorber［J］.Beijing Institute of Technology，2007，16(1) : 23－27.

［10］周长城，顾亮.减振器叠加节流阀片与节流阀开度研究［J］.流体机械，2006，34(7) : 19－23.

［11］周长城.汽车减振器设计与特性仿真［M］.北京:机械工业出版社，2012.

［12］陈轶杰，顾亮，管继富.减振装置节流阀片均布载荷变形解析计算［J］.重庆大学学报:自然科学版，2008，31(9) : 988－991.

［13］成大先.机械设计手册［M］.第3版.北京:化学工业出版社，1994.

［14］WEIZANG C.Large deflection of a circular clamped plate under uniform pressure［J］.Chinese Journal of Physics，1947(2) : 102－113.

(责任编辑:李孟良)

Comparative Study of Finite Element of Large Deflection of Circular Thin Plates

CHEN Jie－ping，LI Jin，QIAO Yin－hu
(College of Mechanical Engineering，Anhui Science and Technology University，Fengyang 233100，China)

Abstract:Annular thin plate is an important part of automobile shock absorber，which belongs to the typical nonlinear deformation of large deflection.Traditional calculation method will cause large errors，or complicated calculation which can not be used in engineering conveniently.With the aid of and modern engineering analysis software，the large deflection of circular thin plate of different shock absorbers specifications were studied using the method of finite element analysis.According to von Kármán differential equation，combining with Chien perturbation method，the analytical expression of the large deflection were presented.Undetermined coefficients of the analytical expression were been fitting out.For different situations，such as fixed radial ratio，or inner/outside diameter，the calculation analysis and error comparison were carried out.Numerical calculation showed that the method is reasonable and reliable，simple and quick，with an error below 3%，and precision is higher，which can meet with the needs of engineering design and analysis.

Key words:Circle thin plate; Large deflection; Finite element; Chien perturbation method

中图分类号:U461.4; U467

文献标识码:A

文章编号:1673－8772(2016) 02－0032－07

收稿日期:2015－12－10

基金项目:安徽省优秀青年基金重点项目(2013SQRL062ZD) ;安徽科技学院青年基金(ZRC2013337)，安徽科技学院重点建设学科(AKZDXK2015C03)。

作者简介:陈杰平(1963－)，男，河南省巩义市人，博士，教授，主要从事机械CAD和控制研究。