环境温度对飞机部件测量数据的影响

张　俐，王炜辰

(北京航空航天大学，北京 100083)

环境温度对飞机部件测量数据的影响

张俐，王炜辰

(北京航空航天大学，北京 100083)

摘要：采用激光跟踪仪检测数据作为研究依据，从被测对象在工程应用环境下的热变形与仪器自身受温度影响所引入的不确定度变化趋势两个方面对测量结果进行评定，分析了计算热变形过程中模型简化的可行性并绘制出相应的温度-不确定度趋势线。

关键词：激光跟踪仪；热变形；温度-不确定度趋势线

1引言

飞机产品气动外形装配要求的不断提高，促进了数字化测量技术与设备的不断发展。在飞机产品装配过程中，除了传统的内应力、自重、制造误差等因素会对飞机部件装配精度产生影响外[1]，由于受生产检测环节的实际工作环境所限，检测人员往往不能将环境温度控制在理想条件下，因此产生的热变形误差与仪器测量误差对最终装配精度的影响同样不可忽略。

针对上述情况，本文从测量条件误差与仪器测量过程中受温度影响所引入的不确定度变化趋势两方面入手，采用机翼前缘模拟样件作为被测对象，应用简化后的模型计算其理论热变形量，并与实际测量数据进行对比，分析影响热变形量的相关因素。同时，应用不确定度相关理论计算在不同环境温度下激光跟踪仪测量数据的不确定度，从而绘制出对应的温度-不确定度趋势线。

2模型简化可行性分析

飞机部件通常由若干零件装配而成，结构比较复杂，采用规则零件在无约束状态下的热变形分析方式对其进行研究并不适合。为保证部件在后续装配中的精度要求，应先对其相应工艺关键特征进行分析并提取检验测量点，而后依据测量点所属的结构与位置对部件进行简化并计算热变形量。

2.1测量点提取

就机翼前缘模拟样件而言，装配过程中的具体约束状态如图1所示。通过铰链上交点孔与工装固定，上部用V型卡板卡紧以限制其摆动。

图1　机翼前缘装配状态示意图

由于模拟样件后续整体装配精度主要靠交点孔位置进行保证，故试验选用其两个外端铰链上的外侧交点孔作为检验测量点，以机翼展开方向作为测量方向，以两点之间的距离作为测量结果，具体如图2所示。

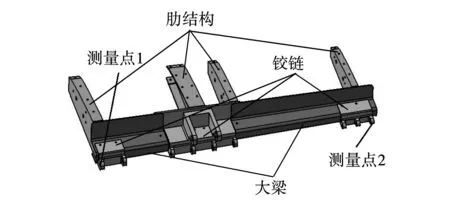
图2　机翼前缘模拟样件数模

2.2简化模型热变形分析

模拟样件与工装固定处为大梁与铰链结合的分段式结构，连接处用螺栓连接。垂直方向有4个依次分布的肋，由于其方向与被测方向垂直，故不会对所选机翼展开方向热变形产生影响。

综上所述，结合所选测量点位置，考虑将该模拟样件简化为由大梁与铰链组成的杆状零件进行理论分析，并采用ABAQUS软件对该想法进行仿真验证。

在具体分析过程中，若假设工装交点孔位置固定不变，即工装在任何温度下热变形为零，则需对所有交点孔位置处设置边界条件，并将环境温度由设计温度22℃上升至26℃，得出上述结构的热变形位移运算结果，如图3所示。

图3　约束状态下仿真结果示意图

从图3分析结果可知，受工装在各交点处的固定作用，机翼展开方向热变形几乎为零，但会造成部件其它部位的严重翘曲，这在实际的生产过程中是不允许的。

为了解决这一问题，减少部件因环境温度变化而产生的内应力与热变形，工程实际应用中常将工装与装配部件采用同一材料进行制造[2]。这样既可以保证两者连接处的热变形量一致，以减少部分装配应力，又可以起到对部件装配过程中的固定作用，以保证装配精度。在该条件下，部件热变形可以忽略工装对大梁交点孔处的约束作用，近似于自由状态，其仿真结果如图4所示。

图4　无约束状态下仿真结果示意图

由此，认为该结构在环境温度变化情况下，其热变形方向沿测量方向均匀分布，故可以将其按杆类零件计算理论热变形量，并与后续实际测量结果进行对比，分析相关影响因素。

3试验方案

本试验测量条件模拟飞机部件装配实际操作环境，采用机翼前缘模拟样件作为被测对象，拆去其蒙皮等非关键结构。同时，为了保证样件的完整性且更贴近实际变形情况，故在测量过程中不对肋结构进行拆除，如图5所示。

图5　机翼前缘模拟样件

试验方案采用数理统计法，4个水平分别为17℃、22℃、26℃和30℃，其中，22℃为飞机设计状态下的理论环境温度。4个温度均为实际生产过程中，在不同季节不同时点下可测量到的现场温度。

试验开始前，先将被测对象放置在22℃的理论温度下24h，并将此状态下测量得到的外端两交点孔之间的距离作为理论长度。在此基础上，将被测对象依次放置在其他3个待测温度下进行测量，对每个温度采集30组数据，最后通过与理论值的比较得出理论-实际长度线。此外，在试验过程中，应保证除温度以外的其他干扰因素，如空气扰动、光照、大气压强等数值稳定，以排除其对试验结果的影响。

4热变形分析

试验以22℃环境下实际测量得到的883.237mm作为设计长度，并通过公式(1)计算被测样件在不同温度下的理论长度，公式如下：

ΔL=αLΔT

(1)

式(1)中，α为材料热膨胀系数。将计算结果与实际测量结果进行比对，具体如图6所示。

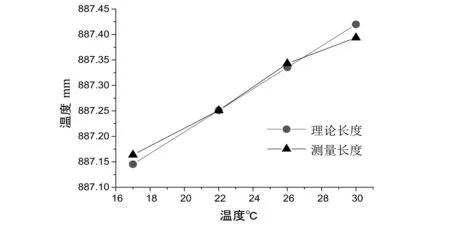
图6　理论—实际长度对比

由图6可知，当温度由22℃上升到26℃时，理论值与测量值基本相符。而当温度下降到17℃或上升到30℃时，实际测量的缩短或者伸长量都小于理论计算量。

造成上述结果主要有以下两方面原因：(1)材料的热膨胀系数实际并非常数，而是经过大量试验所取得的平均值，其取值带有一定的不确定度。热膨胀系数不仅与材料有关，也会受到温度的影响[3]。(2)由于被测样件是分段结构，每两段结构间靠螺栓连接，该连接形式在热变形中可能会由于接触面之间的应力作用影响最终的测量结果。

针对上述第二点原因，在ABAQUS下建立相应仿真模型，模拟板与板之间的螺栓连接状态。在该仿真分析中，受剪连接模型包含了3组共5个接触，分别是螺帽与连接板之间的接触、两个连接板之间的接触和螺栓杆与螺栓孔之间的接触。

为了更直观地揭示螺栓对部件连接处热变形的影响，将有螺栓与无螺栓状态下的仿真结果进行对比，如图7、图8所示。

图8　自由状态分析结果

由图中分析结果可知，在板材均匀受热的情况下，孔与螺栓接触面产生的内应力会阻碍该部分的热变形，使整体变形量减小。同时，通过调节仿真中温度参数至不同数值可知，温度变化越大，对整体测量值影响越大。

综上所述，整体热变形的分析过程中可以对模型进行简化，但也应考虑零件内部或零件之间相互约束关系所带来的影响。

5温度—不确定度趋势分析

激光跟踪仪作为数字化测量手段，已经被广泛应用于航空航天检测、汽车船舶制造等各个领域[4-6]。针对激光跟踪仪的误差研究也涉及多个方面，如转站误差、测距误差、测角误差等。由于仪器自身携带的温度传感器能够对测量数据受温度影响产生的测量误差进行补偿，故在上述文献中均假设环境温度对测量结果没有影响。

该假设前提主要有以下两方面不足：(1)温度传感器自身带有不确定度，其测量精度不能达到100%，故不能完全补偿温度所引入的误差。(2)环境温度的变化会对仪器内部零部件的工作状态产生影响，该影响造成的误差难以用数学方法量化归纳并进行补偿。

此外，温度通过影响激光跟踪仪中光的传播频率，也会影响激光干涉仪的测距结果，艾德伦经验公式可以表示为：

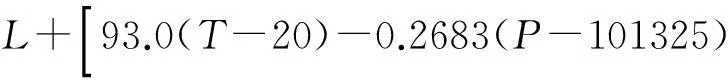
(2)

式(2)中，L为标准激光干涉仪标称波长在测量环境条件下测得的位移值，m；T为光路的平均温度，℃；P为光路的气压，Pa；F为光路中的空气水蒸气分压，Pa。

因此，研究温度对激光跟踪仪测量数据不确定度的影响是必要的。将不同环境温度下得到的试验数据汇总，并将其绘制成数据分布图，如图9-图12所示。

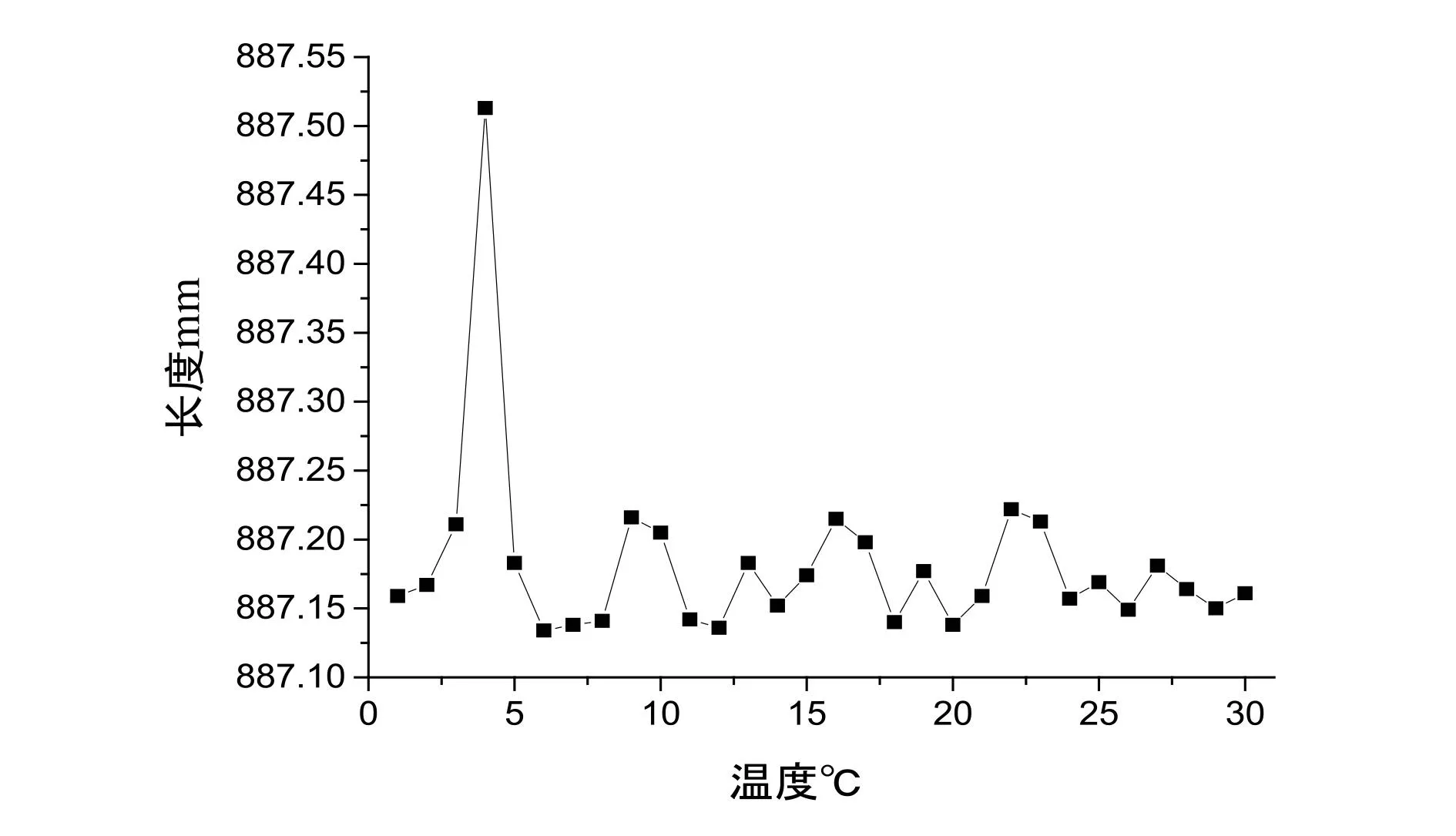
图9　17℃数据分布图

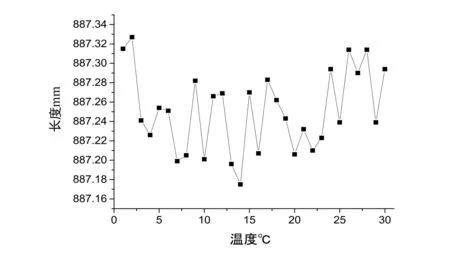
图10　22℃数据分布图

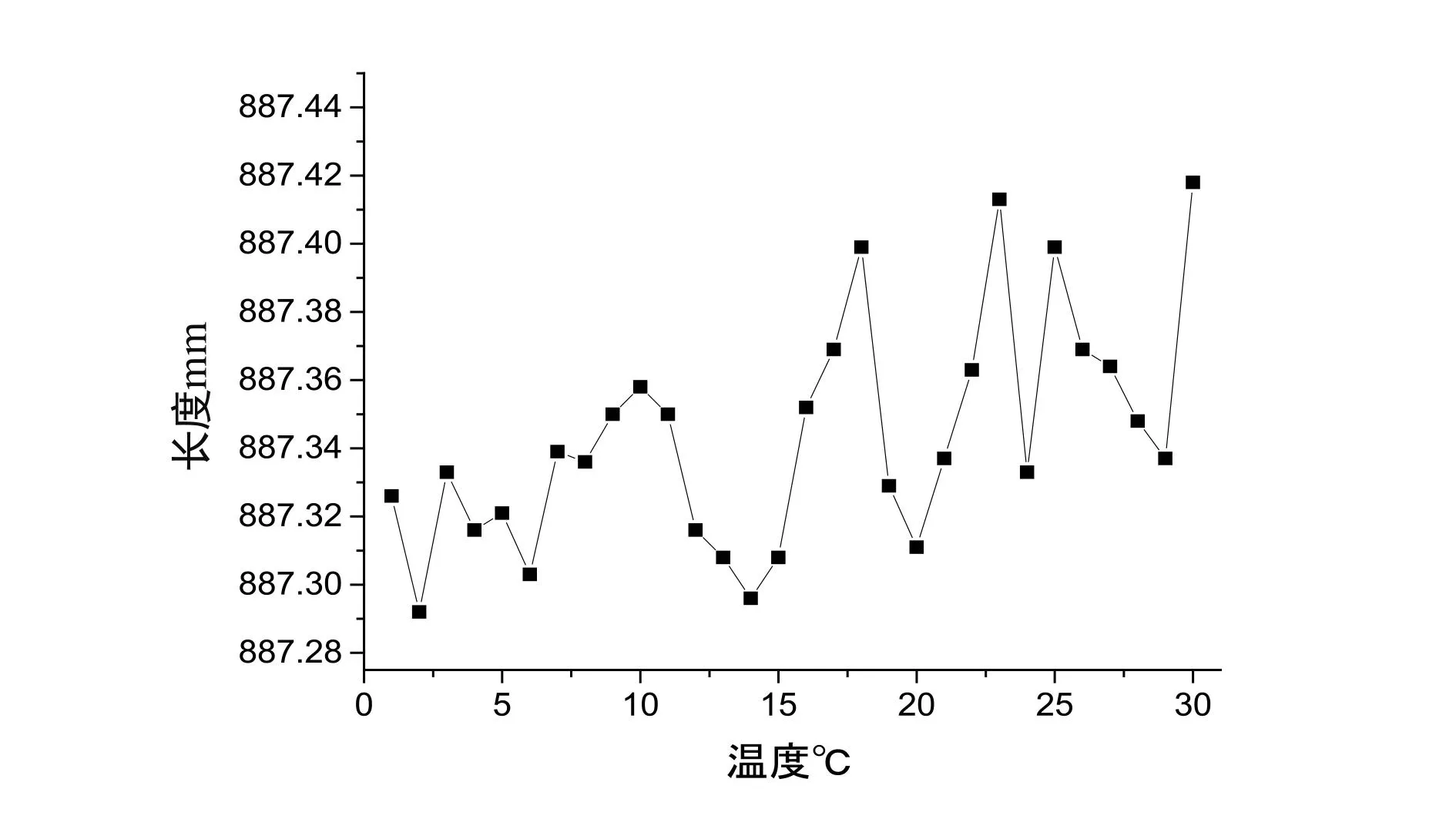
图11　26℃数据分布图

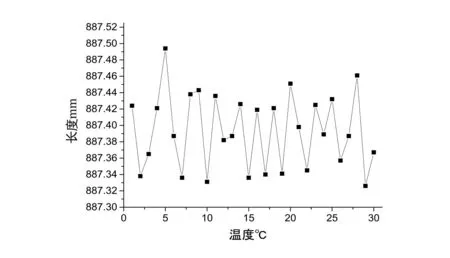
图12　30℃数据分布图

从数据分布图可以清晰地看出每组数据的波动状态。在图9中，由于第4个测量点的测量值大大高于其他测量点，分析原因是靶球基座的松动所致，为粗大误差点，故在之后的不确定度计算过程中对其进行删除。

通常情况下，评价试验结果的最终不确定度采用A类与B类相结合的方式，即：

(3)

针对上述试验数据，A类不确定度的计算表达式为：

(4)

变量Xi在相同条件下独立测量得到的xi1，xi2，…，xin观测列见式(5)，最终计算结果如表1所示。

(5)

表1　A类不确定度

B类不确定度主要是传感器测量误差引入的不确定度，参考艾德伦公式，主要分为以下3个方面：

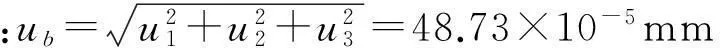
由上述结果可知，B类不确定度与A类不确定度相比数值较小，可忽略不计。最终的计算结果以温度为横坐标、不确定度为纵坐标绘制成图，如图13所示。

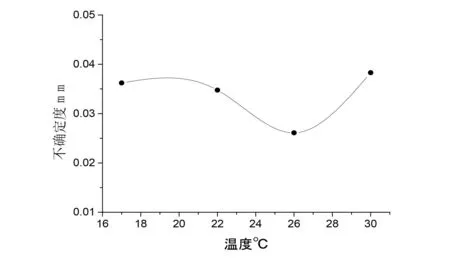
图13　温度—不确定趋势线

由图13的趋势线可知，在24℃-28℃左右的不确定度相对较小，实际操作时，应优先选择在该环境温度下对试验对象进行测量。

该分析结果在环境温度取值范围上跨度较大，主要由以下两个方面原因造成：(1)一般的温度传感器精度为±0.5℃，当试验各组之间取值范围缩小时，由温度传感器测量温度所带来的偏差会影响试验结果的分析，从而会对不确定度的评定产生影响；(2)在一般试验条件下，难以达到试验设计对硬件条件的要求。

6总结

非设计温度下，按照理论的工艺要求进行飞机部件的装配会使整体产生一定内应力，通过模型简化计算被测对象的理论热变形量，并给予相应的位置补偿可以减少上述现象的发生。同时，研究温度对测量仪器不确定度的影响，可以应用温度-不确定度的趋势分析更好地评价不同环境温度下所得到的测量数据结果。

试验中所述的机翼前缘模拟样件模型简化过程是在分析了测量点位置以及自身结构以后得出的，不同的研究对象应遵循该思路具体分析。

综上所述，本文通过将实际测量数据与模型简化后计算出的热变形量进行对比，验证了模型简化方法的可行性，同时对影响热变形的相关因素以及温度-不确定度趋势进行分析。结合以上两者，可以更好地对环境温度引入的误差进行控制，从而提高生产制造装配过程中的整体精度。

参考文献

[1]梁涛.飞机柔性装配误差累积与容差分析技术研究[D].沈阳航空航天大学,2013.

[2]田欢欢.飞机工装典型结构的快速设计[D].南京航空航天大学,2014.

[3]卢荣胜.简单形体零件受温变形理论及其应用研究[D].合肥工业大学,1995.

[4]孙大许,马强,闫勇刚,等.激光跟踪测量系统原理及在制造业中的应用[J].机械,2005,32(8):56-56.

[5]邵建新,邱自学,袁江,等.大量程自由曲面的自适应跟踪测量方法研究[J].中国机械工程,2009,20(9):1045-1047.

[6]Greenleaf A H,Watson J T.Self calibrating contour measuring system using fringe counting interferometers:U.S.Patent 4,457,625[P].1984-7-3.

Influence of Ambient Temperature on Measurement Data of Aircraft Parts

Zhang Li,Wang Weichen

(BeiHang University,Beijing 100083,China)

Abstract：The measurement data of laser tracker is used as the research basis,and the measurement results are assessed from the aspects of the thermal deformation and instrument uncertainty trend affected by the ambient temperature.Then,the feasibility of simplified model is verified,and the corresponding temperature-uncertainty trend lines are drawn.

Keywords:laser tracker;thermal deformation;temperature-uncertainty trend line

[收稿日期]2016-02-23

[作者简介]张俐(1961-)，女，北京人，高级工程师，主要研究方向：飞机数字化装配检测技术。

[基金项目]资助项目(2014ZX04001-081-07)；资助项目(2013E11222)。

中图分类号：V214.1+1

文献标识码：B

doi：10.3969/j.issn.1674-3407.2016.01.003