基于LVQ工况识别的混合动力汽车自适应能量管理控制策略

邓　涛　卢任之　李亚南　林椿松

重庆交通大学，重庆，400074

基于LVQ工况识别的混合动力汽车自适应能量管理控制策略

邓涛卢任之李亚南林椿松

重庆交通大学，重庆，400074

摘要：为提高混合动力汽车的燃油经济性，选取6种典型行驶工况代表“市区”、“郊区”和“高速公路”3类主要工况，采用基于规则的模糊能量管理控制策略，以整车燃油经济性为目标，在3类主要工况下用改进型粒子群优化算法优化发动机联合工作曲线与发动机关闭曲线系数，得到相应的优化后的隶属度函数的参数；运用学习向量量化(LVQ)算法识别车辆运行工况，动态选择相应的模糊控制策略，使混合动力汽车控制策略对选定的几种代表性工况具有自适应性，从而提高整车的燃油经济性。仿真对比结果表明，相比于传统混合动力汽车，燃油经济性提高了3.4%。

关键词：混合动力汽车；工况识别；燃油经济性；粒子群优化算法；学习向量量化(LVQ)算法

0引言

运行工况对混合动力汽车(hybrid electric vehicle,HEV)的燃油经济性与排放性影响较大，是设计与评价混合动力汽车的一项重要指标，也是能量管理控制策略必须考虑的关键因素。然而,当前大多数能量管理控制只考虑单一工况，燃油经济性的提升受到局限，而且无法使控制策略适应各种不同工况。Williamson等[1]对并联柴-电混合巴士在7种运行工况下进行研究，发现柴油机具有不同效率和运行参数。Sharer等[2]在past软件中建立了经典混合动力模型即Toyota Prius和Ford Focus汽车模型,在多种运行工况下仿真分析得出运行工况对混合动力汽车的影响比对传统汽油机汽车的影响要大。汽车的运行工况是混合动力汽车控制策略制定的必要条件，工况的不同会对控制策略的发挥有影响，进而影响整车的燃油经济性与排放性。所以,对混合动力汽车的运行工况进行识别，从而采用相应工况的控制策略参数，建立满足不同工况的控制策略越来越重要[3-5]。

本文以NYCC、MANHATTAN、WVUSUB、CSHVR、US06_HWY、HWFET 6种典型工况代表车辆的6种不同行驶工况，作为仿真道路行驶工况,这6种工况涵盖了“市区”、“郊区”、“高速公路”3类主要工况[6]，以基于规则的控制策略为基础，以整车燃油经济性为优化目标，采用改进的粒子群优化(particle swarm optimization，PSO)算法优化发动机联合工作曲线系数和发动机关闭曲线系数，采用学习向量量化(learning vector quantization， LVQ)算法对行驶工况进行识别，得到基线法中3个参数优化后的取值，由此得到以上几种工况下各自不同参数的能量管理控制策略，该控制策略能够适应以上几种不同工况，并且可有效提高整车燃油经济性。

1基于规则的发动机基线控制策略

以某并联式中度混合动力汽车为研究对象，整车结构如图1所示，整车参数配置如表1所示。图1中，AMT表示机械自动变速器(auto mechanical transmission)。

图1　某型并联式中度混合动力汽车结构

名称项目参数整车部分整备质量(kg)1535发动机发动机型号1.0LSI排量(L)1.0峰值(kW)47最高转速(r/min)5700动力电池电池类型锂电池额定容量(A·h)6额定电压(V)290.5AMT挡位数6电机额定功率(kW)75额定电压(V)240

为了达到实车运用的目的，采用了简单的基于规则的发动机基线控制策略[7]，如图2所示。设Treq为混合动力汽车的需求转矩，Tm为电机转矩(放电为正，充电为负)，Te为发动机输出转矩，基本控制规则如下：

图2　HEV发动机工作区域控制策略

(1)当车速v低于某一值或者需求转矩Treq小于某一值时，电机单独提供驱动转矩， Treq=Tm。

(2)当发动机在给定转速与需求功率下高效率工作时，发动机单独驱动，Treq=Te；并且当蓄电池荷电状态(SOC)值较低时，发动机驱动汽车的同时给电池充电，Treq=Te+Tm，此时Tm为负值。

(3)当汽车的需求转矩Treq较大、超过了发动机的最优效率曲线时，发动机与电机同时提供汽车所需转矩，Treq=Te+Tm。

(4)当混合动力汽车运行于怠速模式并且电池的SOC值较低时，发动机提供需求转矩Treq的同时驱动发电机给电池充电，Treq=Te+Tm；如果电池SOC充足，则发动机停止工作，电机提供需求转矩，Treq=Tm。

(5)当电池SOC值低于电池SOC值的上限时，混合动力汽车制动时，制动能量通过电机转化为电能给电池充电,Treq=Tm。

由此建立整车控制策略，如图3所示。

图3　基于工况识别的控制策略

2模糊控制器

基线法控制策略就是将发动机外特性曲线乘以某系数，得到发动机联合工作曲线和发动机关闭曲线，它一定程度上确定了混合动力源分配。但是基线法控制策略并没有优化发动机联合工作曲线系数与发动机关闭曲线系数。考虑到系统精确的数学模型难以确立且其他全局优化算法计算量大，目前难以有实车运用的可能，而模糊控制器计算量小，鲁棒性好，因此本文采用模糊控制器控制发动机联合工作曲线系数和发动机关闭曲线系数。如图2所示，Temin对应的曲线系数为K1，Temax对应的曲线系数为K2，K1与K2的初始值为0，K1∈[-1, 1], K2∈[-1, 1]。取值为1时对应曲线向上平移200N·m，取值为-1时对应曲线向下平移200N·m。K1与电池SOC以及电机转速有关，K2影响到发动机的高效工作区域，与电池SOC、电机转速、汽车需求转矩Treq有关。模糊控制器的输入变量为这些对参数有影响的量，即SOC值、电机转速ωe和需求功率Treq，输出为K1、K2。

采用带参数的三角形隶属度函数作为模糊控制器的隶属度函数，输出变量K1的模糊语言变量为{VS(很小)，S(小)，LS(稍小)，M(中)，LL(稍大)，L(大)，VL(很大)}。定义输出变量K1的隶属度函数VS的论域为[-100, P1, P2]，定义函数S的论域为[P3, P4, P5]，定义函数LS的论域为[P6, P7, P8]，定义函数M的论域为[P9, P10, P11]，定义函数LL的论域为[P12, P13, P14]，定义函数L的论域为[P15, P16, P17]，定义函数VL的论域为[P18, P19, 100]。输入变量蓄电池SOC值的模糊语言变量为{VL(很低)，L(低)，LL(稍低)，LH(稍高)，H(高)，VH(很高)}；定义函数VL的论域为[-100, P20, P21]，定义函数L的论域为[P22, P23, P24]，定义函数LL的论域为[P25, P26, P27]，定义函数LH的论域为[P28, P29, P30]，定义函数H的论域为[P31, P32, P33]，定义函数VH的论域为[P34, P35, 100]。输入变量电机转速的模糊语言为{VS(很慢)，S(慢)，LS(稍慢)，LF(稍快)，F(快)，VF(很快)}；定义电机转速的隶属度函数VS的论域为[-100, P36, P37]，定义函数S的论域为[P38, P39, P40]，定义函数LS的论域为[P41, P42, P43]，定义函数LF的论域为[P44, P45, P46]，定义函数F的论域为[P47, P48, P49]，定义函数VF的论域为[P50, P51, 100]。

同理，K2的模糊隶属度函数选择三角形隶属度函数，输入变量蓄电池SOC值的模糊语言变量定义与上文相同，不再赘述。输入变量需求转矩Treq的模糊语言变量为{VS(很小),S(小),LS(稍小),LB(稍大),B(大),VB(很大)}；定义汽车需求转矩的隶属度函数VS的论域为[-100, P53, P54]，中间的定义与上文的相同，不再赘述。定义函数VH的论域为[P89, P90, 100]。两者的模糊规则如表2、表3所示。

表2　K1的模糊控制规则表

表3　K2的模糊控制规则表

3基于改进型PSO算法的隶属度函数

PSO算法相对于其他智能算法具有参数设置简单、收敛速度快的优点，且适用于非线性寻优问题，对于像隶属度函数参数较多的问题应用起来特别方便。由于标准PSO算法收敛速度慢，容易陷入局部最优，因此采用改进型PSO算法优化模糊控制器隶属度函数参数。对标准PSO算法收敛速度过慢、迭代后期容易陷入局部最优的缺陷进行改进，引入自适应权重因子与突变因子，当粒子的最优位置变化很小，如前后位置差值的绝对值小于0.001时，可认定粒子群陷入局部优化，保留记录这个陷入局部优化的解的坐标点，以此位置为基础，将10%的粒子重新随机初始化，在记录下来的陷入局部最优解的坐标位置的基础上，以变异数值(介于0.05～0.1)为半径随机分布粒子群的位置。为了在获得全局优化效果的同时不影响收敛性，惯性权重因子w的取值应该是：迭代初期取值比较大，达到一定迭代次数后w的取值变小。惯性权重用下式进行调节：

(1)

式中，fbest(t)为种群历史最佳位置的适应值；fpi(t)为第i个粒子个体历史最佳位置的适应值；r为(0，1)之间的常数；N为种群中粒子个数。

以粒子的最佳适应值与种群的历史最佳的适应值的“距离”作为惯性权重调节依据。该距离越小w越小，集中搜索以保证最优解收敛；该距离越大，w越大，保证全局性的搜索。

本文以燃油经济性为粒子群算法优化的目标，上述模糊控制器的隶属度函数的参数作为算法的粒子群，改进的PSO算法的优化流程如图4所示。

图4　改进的PSO算法的优化流程

4典型行驶工况

实际道路的行驶工况比较复杂，混合动力汽车在实际运行中可能连续运行于各种复杂的行驶工况。本文选取6种行驶工况作为3类典型工况：代表城市中心道路工况的NYCC和MANHATTAN，代表郊区道路工况的WVUSUB和CSHVR，代表高速路工况的US06_HWY和HWFET，如图5所示。

(a)WVUSUB(b)CSHVR

(c)US06_HWY(d)HWFET

(e)NYCC(f)MAHATTAN图5　6种典型工况

5基于LVQ方法的工况识别

5.1工况特征参数的计算

根据以往研究结果，如果采用的工况历史数据样本时间长度太小，则可能不能正确地包含循环工况的特征信息，相反，如果采用的样本时间长度太大，则在实时控制情况下计算负担太大[8]。另外，样本时间数据段也是可以变化的，但为了方便计算运行，采用固定时间段。根据以往研究，大部分时间样本工况片段选取在150～300 s之间。综上所述，为了获取道路工况特征参数的样本数据，将道路工况分成片段，每个片段为180 s，并且可以叠加[4]，叠加选择情况如图6所示，1～9代表工况片段的序号。

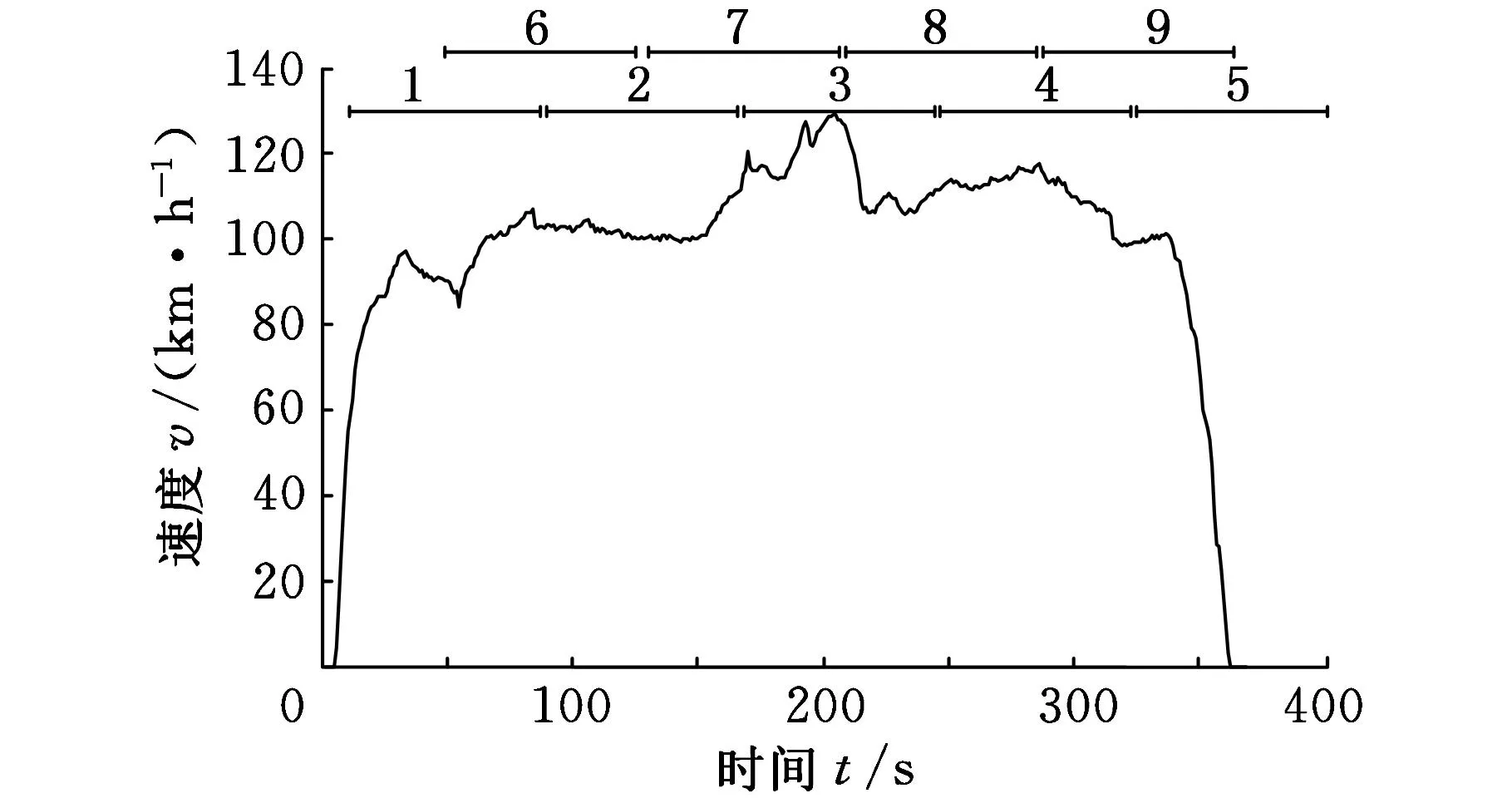
图6　道路工况分段示意图(US06_HWY)

5.2道路工况的特征参数选取

道路工况的特征参数原则上是要包含各自循环工况的特征，但工况的特征参数选取太多的话，计算量太大；特征参数选取太少则不能正确包含循环工况的特有信息，工况识别的误差太大。为了达到特征参数选择最优化，必须满足每个特征参数各自独立地包含一种工况特征信息，根据文献[9]的研究，特征参数种类选取平均速度、正向平均加速度(a>0.1 m/s2)、低速(15～30 km/h)时间比例、中高速(70～90 km/h)时间比例、高速(>90 km/h)时间比例、极低减速度(a<-2.5 m/s2)时间比例、高减速度(a<-2 m/s2且a>-2.5 m/s2)时间比例、最大循环工况加速度(m/s2)、最大循环工况速度(km/h)、工况速度标准差(km/h)、中等减速度(a<-1 m/s2且a>-1.5 m/s2)时间比例、中高减速度(a>-2 m/s2且a<-1.5 m/s2)时间比例、高加速度(a>1.5 m/s2且a<2.5 m/s2)时间比例、极高加速度(a>2.5 m/s2)时间比例。

5.3LVQ神经网络方法介绍

用于工况识别的分类识别算法有贝叶斯归类算法、决策树、粗集理论、模糊聚类分析算法、LVQ算法、支持向量机等。支持向量机模式识别方法特别适用于二维的问题， LVQ神经网络结合了竞争学习与监视学习算法，已经成功应用于模式识别、数据压缩等领域。对于工况识别问题，神经网络比较常用，因此采用LVQ算法作为行驶工况识别的方法。LVQ神经网络由三部分组成：输入向量层、竞争层、线性输出层，其结构如图7所示。图7中，P为R维的输入模式；R表示输入训练样本向量的维数；上角标1、2分别表示竞争层、线性输出层；S为神经元的个数；n为神经元的输入；a为神经元的输出；IW(1,1)为输入层神经元与竞争层神经元的权系数矩阵；LW(2,1)为竞争层神经元与线性输出层神经元之间的连接权系数矩阵；‖ndist‖表示求两个多维度向量组的距离；compet(·)表示竞争层神经网络计算处理；purelin(·)表示线性输出层神经网络计算处理 。

图7　LVQ神经网络结构

道路工况有10个特征参数，因此输入层有10个节点。竞争层通过竞争学习算法对输入向量进行分类。通过了学习算法处理的类称之为子类，这些子类被分为明确定义的目标类。线性输出层的6个神经元代表6种道路工况，采用第二代LVQ神经网络算法(即LVQ2算法)来训练样本，以提高分类的正确率。训练80代后，识别误差降到0.01。当识别误差不再下降之后，可认为神经网络训练过程完成。具体实现过程参见文献[10]。分段计算后得到3类典型工况的训练样本，然后进行神经网络训练，获取工况识别参数。

6仿真分析

6.1典型工况模糊控制器参数获取

按照图4所示的流程将上述6种行驶工况输入到改进型PSO算法模型中，经过改进型PSO算法优化后得到“城市”、“郊区”、“高速公路”3类典型工况的模糊控制器隶属度函数的参数。因为隶属度函数参数比较多，在此仅列出NYCC工况优化后的隶属度函数参数取值，如表4所示，其他工况的参数不一一列出。

6.2实时工况识别仿真分析

将上述6种行驶工况以混合搭配的方式组合形成一个大的实时测试工况，其中1代表城市工况，2代表郊区工况，3代表高速路工况，依次类推。然而，针对整个工况直接进行工况识别，难度较大，而且准确性不高。因此，采取工况分段识别的方法，不仅能提高燃油经济性[11]，而且可大大提高识别精确性。时间段选择180s，然后进行仿真分析，测试工况如图8所示，模式识别结果如图9所示。

表4　NYCC工况控制策略模糊控制器的优化结果

图8　测试工况图

图9　工况识别模式结果

因为工况被划分为片段的形式进行工况识别，所以片段之间可能会因为划分得过于相似，使得LVQ神经网络算法识别产生误差，但LVQ神经网络算法是可以大致识别出工况类型的。将得到的结果输入到控制策略中，进行整车控制策略的仿真分析，其自适应过程如图10所示。

图10　基于LVQ算法识别的自适应控制示意图

基于LVQ神经网络算法的工况识别的控制策略与无工况识别的基本模糊规则控制策略仿真结果对比如表5所示，表中数据是6种工况统计结果的平均值。

表5　工况识别计算结果

注：SSOC，e为仿真运行结束时的SOC值，SSOC，s为仿真运行开始时的SOC值。

从表5结果中可以看出，采用LVQ神经网络算法工况识别后，混合动力汽车的燃油消耗减少了3.4%，SOC值变化减小了2.7%，SOC值波动(即SSOC，e-SSOC，s)减小了19.64%，因此采用有工况识别的控制策略的混合动力汽车在以上6种工况下运行，总的百公里燃油消耗可减少3.4%。

7结论

(1)在基本的规则控制策略的基础上建立了以发动机关闭曲线、发动机联合工作曲线为基础的工作区域动态调整的模糊能量管理控制策略。

(2)采用改进的PSO算法优化发动联合工作曲线系数与发动机关闭曲线系数， 得到三类典型工况的模糊控制器的参数。

(3)利用LVQ神经网络算法的模式识别能力在组合工况下仿真分析，使混合动力汽车在不同工况下采用相应的模糊能量管理控制策略，由Simulink模型仿真结果可知，相比一般的无工况识别与算法优化的模糊控制策略，该能量管理控制策略可使整车百公里油耗减少3.4%。

参考文献：

[1]Williamson S S, Emadi A, Dewan A. Effects of Varying Driving Schedules on the Drive Train Efficiency and Performance Characteristics of a Parallel Diesel-Hybrid Bus[J].SAE Technical Paper, 2005-01-3477.

[2]Sharer P, Leydier R, Rousseau A. Impact of Drive Cycle Aggressiveness and Speed on HEV’s Fuel Consumption Sensitivity[J].SAE Technical Paper, 2007-01-0281.

[3]Jeon Soon-Il, Jo Sung-Tae, Park Yeong-Il,et al.Multi-Mode Driving Control of a Parallel Hybrid Electric Vehicle Using Driving Pattern Recognition[J]. Journal of Dynamic Systems, Measurement, and Control, 2002,124(1):141-149.

[4]Langari R, Won Jong-Seob. Intelligent Energy Management Agent for a Parallel Hybrid Vehicle-Part I: System Architecture and Design of the Driving Situation Identification Process[J]. IEEE Transactions on Vehicular Technology, 2005, 54(3): 925-934.

[5]田毅, 张欣, 张良, 等. 神经网络工况识别的混合动力电动汽车模糊控制策略[J]. 控制理论与应用, 2011,28(3):363-369.

Tian Yi, Zhang Xin, Zhang Liang, et al. Fuzzy Control Strategy for Hybrid Electric Vehicle Based on Neural Network Identification of Driving Conditions[J]. Control Theory & Applications,2011,28(3):363-369.

[6]吴剑. 并联式混合动力汽车能量管理策略优化研究[D] 济南: 山东大学, 2008.

[7]Brooker A, Haraldsson K, Hendricks T, et al.ADVISOR Documentation[EB/OL]. Colorado:National Renewable Energy Laboratory, 2002.http://www.ctts.nrel.gov/analysis/advisor_doc/.html.

[8]Wang R, Lukic S M. Review of Driving Conditions Prediction and Driving Style Recognition Based Control Algorithms for Hybrid Electric Vehicles[C]//Vehicle Power and Propulsion Conference (VPPC), IEEE. Chicago,2011: 1-7.

[9]Feng Lei, Liu Wenjia, Chen Bo. Driving Pattern Recognition for Adaptive Hybrid Vehicle Control[J].SAE Technical Paper, 2012-01-0742.

[10]Jie Xing, Han Xuefeng, Ye Hui, et al. Driving Cycle Recognition for Hybrid Electric Vehicle[C]//Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), IEEE Conference and Expo. Beijing, 2014:1-6.

[11]林歆悠, 孙冬野. 基于工况识别的混联式混合动力客车控制策略研究[J]. 中国机械工程, 2012,23(7):869-874.

Lin Xinyou, Sun Dongye. Development of Control Strategy Fora Series-Parallel Hybrid Electric City Bus Based on Roadway Type Recognition[J]. China Mechanical Engineering,2012,23(7):869-874.

(编辑苏卫国)

Adaptive Energy Control Strategy of HEV Based on Driving Cycle Recognition by LVQ Algorithm

Deng TaoLu RenzhiLi YananLin Chunsong

Chongqing Jiaotong University,Chongqing,400074

Abstract:In order to reduce fuel consumption, six kinds of typical driving cycles were chosen to represent the “urban”, “suburban” and “highway”. And for vehicle fuel economy, based on fuzzy control strategy with rules,an improved PSO algorithm was adopted to optimize the engine working with motor curve factor and the engine shutting off curve factor, then the optimized parameters of membership function could be achieved under the above typical driving cycles. Furthermore, LVQ algorithm was adopted to recognize real-time driving cycle, the corresponding fuzzy control strategy could be chosen according to the recognition results, which maintained the adaptability for those driving cycles, and improved HEV’s fuel economy. Simulation results show that fuel economy adopted with this control strategy is improved by 3.4% comparing to the traditional methods without cycle recognition.

Key words:hybrid electric vehicle(HEV); driving cycle recognition; fuel economy; particle swarm optimization(PSO) algorithm;learning vector quantization(LVQ) algorithm

收稿日期：2015-04-23

基金项目：国家自然科学基金资助项目(51305473)；中国博士后科学基金资助项目(2014M552317)；重庆市基础与前沿研究计划资助项目(cstc2013jcyjA60007)；重庆市教委科学技术研究项目(KJ120421)；重庆市博士后研究人员科研项目特别资助(xm2014032)

中图分类号：U469.72

DOI：10.3969/j.issn.1004-132X.2016.03.025

作者简介：邓涛，男，1982年生。重庆交通大学机电与车辆工程学院副教授。主要研究方向为混合动力控制。发表论文30余篇。卢任之，男，1990年生。重庆交通大学机电与车辆工程学院硕士研究生。李亚南，男，1989年生。重庆交通大学机电与车辆工程学院硕士研究生。林椿松，男，1990年生。重庆交通大学机电与车辆工程学院硕士研究生。