波形曲率延拓在局域均值分解中的应用

魏永合　牛保国　刘雪丽　赵旭宁

沈阳理工大学，沈阳，110159

波形曲率延拓在局域均值分解中的应用

魏永合牛保国刘雪丽赵旭宁

沈阳理工大学，沈阳，110159

摘要：局域均值分解(LMD)是一种能够将复杂的调幅调频信号自适应地分解为一系列单分量的调幅调频信号的处理方法，其分解过程存在端点效应，分解结果有一定程度的失真。针对此问题，提出根据波形曲率特征对信号端点进行极值延拓，通过特征波的曲率波动来筛选与边界波形最为相似的数据段，在此基础上将波形匹配曲率估计应用于LMD分解过程中, 并与镜像延拓及自适应波形匹配延拓方法相比较，验证了所提方法的优点。使用仿真信号与实际的齿轮故障数据进行试验与检测，结果表明，所提方法可以有效改善LMD分解过程的端点效应，提高分解精度。

关键词：局域均值分解(LMD)；端点效应；波形匹配；曲率特征

0引言

Smith[1]于2005年首次提出局域均值分解(local mean decomposition，LMD)方法。作为能够处理信号数据的新的时域故障诊断方法，LMD可以自适应地处理繁琐的非线性、非平稳、多分量的调幅调频信号，将其分解为多个乘积函数(product function,PF)分量。每一个PF分量都由一个包络信号和一个纯调频信号相乘组成，包络信号就是该PF分量的瞬时幅值，由纯调频信号可以直接求出该PF分量的瞬时频率。进一步组合所有乘积函数的瞬时幅值和瞬时频率，便可以获得原始信号完整的时频分布。

经典LMD方法自身有一些缺陷，端点效应就是其中之一。对于迭代筛选分解信号方法中存在的端点效应问题，许多学者已提出了很多改进方法。文献[2-4]针对LMD分解过程，提出使用自适应波形匹配方法来延拓原始信号，然后再进行LMD分解，该方法抑制了端点效应，并在工程实际中得到应用；文献 [5]提出在信号中添加窗函数来抑制经验模态分解(empirical mode decomposition, EMD)过程的端点效应。文献[6]对比分析了端点效应在LMD和EMD分解过程中对分解结果的影响，提出了一种使用镜像延拓方法抑制端点效应的处理技术。文献[7]提出了基于对称差分能量算子解调的LMD端点效应抑制方法。文献[8]针对局域波分解端点效应问题提出使用三角波形相似估计法对信号端点局部均值进行估计。

经过人们的不断研究，已经出现了许多抑制端点效应的技术方法,但是这些方法或多或少存在一些缺陷，如镜像延拓方法通常需要将镜像点置于端点极值处，但实际中往往无法确定端点是否为极值，因此通常会导致结果具有一定程度的失真。本文在目前经典抑制端点效应方法的基础上，提出一种基于信号波形曲率特征的估计匹配法来抑制LMD分解过程中的端点效应，并将该方法与自适应波形曲率延拓以及镜像延拓方法进行对比，选取相关性数据以及能量评价指标[5-6]综合说明该方法的优点。在此基础上将其应用到LMD分解中，通过仿真信号与工程实际案例分析，证明该方法能够有效地抑制端点效应对LMD分解结果的影响，显著提高分解精度，从而为准确提取故障特征提供参考。

1LMD方法及端点效应

1.1LMD基本原理

LMD是一种能够有效处理非线性、非平稳信号的方法，其具体步骤如下：

(1)求出原始信号x(t)的全部局部极值点ni，计算相邻极值点ni和ni+1之间的均值mi:

(1)

将所有的均值mi进行线性直线延拓，获取局部均值线段，对局部均值线段进行平滑处理，获取局部均值函数m11(t)。

(2)根据局部极值点及其时刻，计算局部幅值ai：

(2)

将获得的局部幅值ai进行线性直线延拓，获取信号的局部幅值线段，对局部幅值线段进行平滑处理，获取信号的包络估计函数a11(t)。

(3)从原始信号x(t)中分离出局部均值函数m11(t)，对分离后的信号按照下式进行解调处理：

(3)

h11(t)=x(t)-m11(t)

(4)

假如s11(t)的包络估计函数不等于1，则对s11(t)重复上述迭代过程，直到s1n(t)表现出纯调频信号的特征，即它的包络函数值为1。所以有

(6)

(4)求包络信号a1(t)，即

(7)

(5)计算乘积函数，即

PF1(t)=a1(t)s1n(t)

(8)

(6)从原始信号x(t)中分离PF分量，获取新的信号u1(t)，将其作为对象数据重复上述迭代过程，迭代n次，直至un(t)呈现单调函数的特征为止，即

u1(t)=x(t)-PF1(t)u2(t) =u1(t)-PF2(t) ︙un(t)=un-1(t)-PFn(t)üþýïïïï

(9)

原始信号x(t)被解调处理分解为 n个PF分量和一个余量un(t)，即

(10)

1.2端点效应

LMD分解是以信号的局部极值点作为基础，循环地多次对局部均值函数与局部包络函数等进行迭代处理。但是在迭代过程中，端点以外的极值点情况不能确定，这样就会使分解结果在两端处产生误差，迭代次数越多，这种误差就会越向信号内部扩散，对于低频PF分量，由于时间尺度大，这种误差影响就会更加明显，这就是端点效应。

由LMD原理及过程可知，产生端点误差的主要原因是端点可能不是极值点。假设在求局部均值函数以及局部包络函数时，所使用的端点均是原信号的极值点，这样端点处的误差就会得到抑制，端点效应的影响就会减小。进行LMD分解处理之前，先对对象信号数据进行端点极值延拓，以求更加真实地表现对象信号端点以外的极值分布情况，便于进行后续迭代处理。分解完成以后，按照左右延拓的点数，再对分解结果进行适当的截取。这样就可以抑制端点。

2波形曲率估计延拓及仿真

2.1波形曲率估计延拓

波形曲率估计匹配延拓是一种基于曲线采样点曲率的端点极值预测方法。对信号端部进行极值延拓，在一定程度上可以减轻端点效应，其实现方法关键步骤如下：

(1)截取匹配特征波形，计算特征曲率。定义e(i)为待处理信号x(t)的极值点位置矩阵，选取x(1)-x(e(1))-x(e(2))波段为特征波段，采用多项式拟合方法拟合特征波段离散数据，按照下式计算波段内采样点附近曲率，将其作为特征曲率C：

(11)

(2)划分采样信号。以极值点为基准、特征波段长为步长划分整个采样信号。对模拟信号进行左端延拓，进一步说明该延拓方法步骤。定义采样信号x(t)的极大值、极小值位置的矩阵数组分别为max(i)、min(j)。其中i是从1至m的整数，m是极大值个数；j为从1至n的整数，n是极小值个数。假设信号左端第一个极值点是极大值点，则特征波段就是x(1)-x(max(1))-x(min(1))，特征波形长度为l，图1中波形段a为特征波形段。再以剩余信号内部极小值序列为匹配波形段终点，向左取步长为l的点为起点，截取波形段为匹配波形段，图1中a1即为匹配的第一个波形段，以此类推。

图1　波形段划分示意图

(3)选取指标，寻找最优波形段。选择相关系数ρ及曲率匹配误差ε作为指标进行波形段筛选。采用多项式拟合方法拟合每个波形段采样数据，然后利用式(11)计算n个波形段内采样点附近的曲率Cn(i)。根据下面的公式分别计算特征波段曲率与匹配波段曲率之间的相关系数和匹配误差：

(12)

(13)

式中，Cov(C，Ci)表示特征曲率C与第i个波形段曲率Ci的协方差；D(C)为特征波形曲率的标准差；D(Ci)为第i个匹配波形段内曲率的标准差。

分别设定阈值ρ1、ε1。在匹配波形段集合里搜索出阈值ρC-Ci>ρ1且ε(i)<ε1的波形段为目标波形段。为了更加准确地找出符合信号内部规律的波形段，阈值ρ1、ε1可分别选定为0.999、0.0001，具体阈值设定要视实际情况而定。

(4)以步骤(3)中的目标波形段为基准，截取两个极值长度数据段，延拓到信号一端，按照同样的方法延拓数据另一端。

2.2仿真实验

将波形曲率延拓方法应用于LMD分解中，在进行LMD分解之前进行一次波形曲率延拓。进行仿真实验检验。选取仿真信号x(t)如下：

x(t)=x1(t)+x2(t)

(14)

x1(t)=(1+0.9(sin(0.04πt))cos(0.1πt+sin(0.01πt))

(15)

x2(t)=sin(0.03πt)cos(0.08πt)

(16)

x(t)为两个分量信号的叠加，其中x1(t)为调幅调频信号；x2(t)为调幅信号。t取值范围为[0,500 s]。首先对原始信号x(t)进行波形曲率延拓，延拓左右端两个极值，由于信号的规律性特别强，故设定误差阈值ρ1=0.9999，ε1=0.0001。

延拓前后的信号如图2所示，可以看出，左右端点延拓后的信号趋势非常符合原始信号内部规律。

图2　波形延拓前后信号图像对比

求取延拓前后信号的局域均值线段以及局部包络线段，如图3所示。从图3中可以看出，延拓前后的局部均值线段及局部包络线段端部有所不同。

(a) 延拓前后信号局部均值线段

(b) 延拓前后信号局部包络线段图3　延拓前后信号线段对比

分别求取原始信号及延拓信号的局部均值函数和局部包络函数，如图4所示。从图4中可以看出，原始信号的局部均值函数和局部包络函数在端部有一定程度的失真。

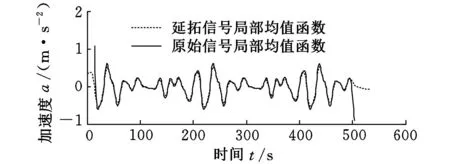
(a)延拓前后信号局部均值函数

(b)延拓前后信号局部包络函数图4　延拓前后信号局部均值函数和包络函数对比

曲率波形延拓后进行LMD分解，得到4阶PF分量如图5所示。由图5可以看出，信号的主要信息集中在前两阶PF分量PF1(t)、PF2(t)中，第3、4阶PF分量PF3(t)、PF4(t)幅值明显减小，不是信息集中区域，为LMD分解的“虚假”成分；u4(t)是残余分量信号。理论上，分解结果只有两阶，出现这些“虚假”成分的主要原因是求局部均值函数和局部包络函数产生的误差以及估计端点极值所产生的延拓误差，这些误差不可避免。

图5　波形曲率延拓后再进行LMD分解的结果

2.3与其他延拓方法对比

将波形曲率匹配延拓法与镜像延拓法及自适应波形匹配方法相比较。取式(14)的仿真信号x(t)为分析研究对象，分析参数的设置也相同。分别比较波形曲率估计匹配法、镜像延拓法及自适应波形匹配方法在LMD方法中的应用及其对端点效应的改进程度。

2.3.1延拓处理及LMD分解对比

采用波形曲率匹配法、自适应波形匹配法、镜像方法对模拟采样信号进行延拓，延拓结果如图6所示。由图6可得出：镜像延拓缺乏自适应性，延拓结果和其他两种方法相比，不是特别满足信号内部规律；波形曲率延拓和自适应波形匹配延拓都能够自适应地选取最优波形段进行极值延拓，但是相比较来说，波形曲率延拓选取的波形段更加符合信号内部规律。

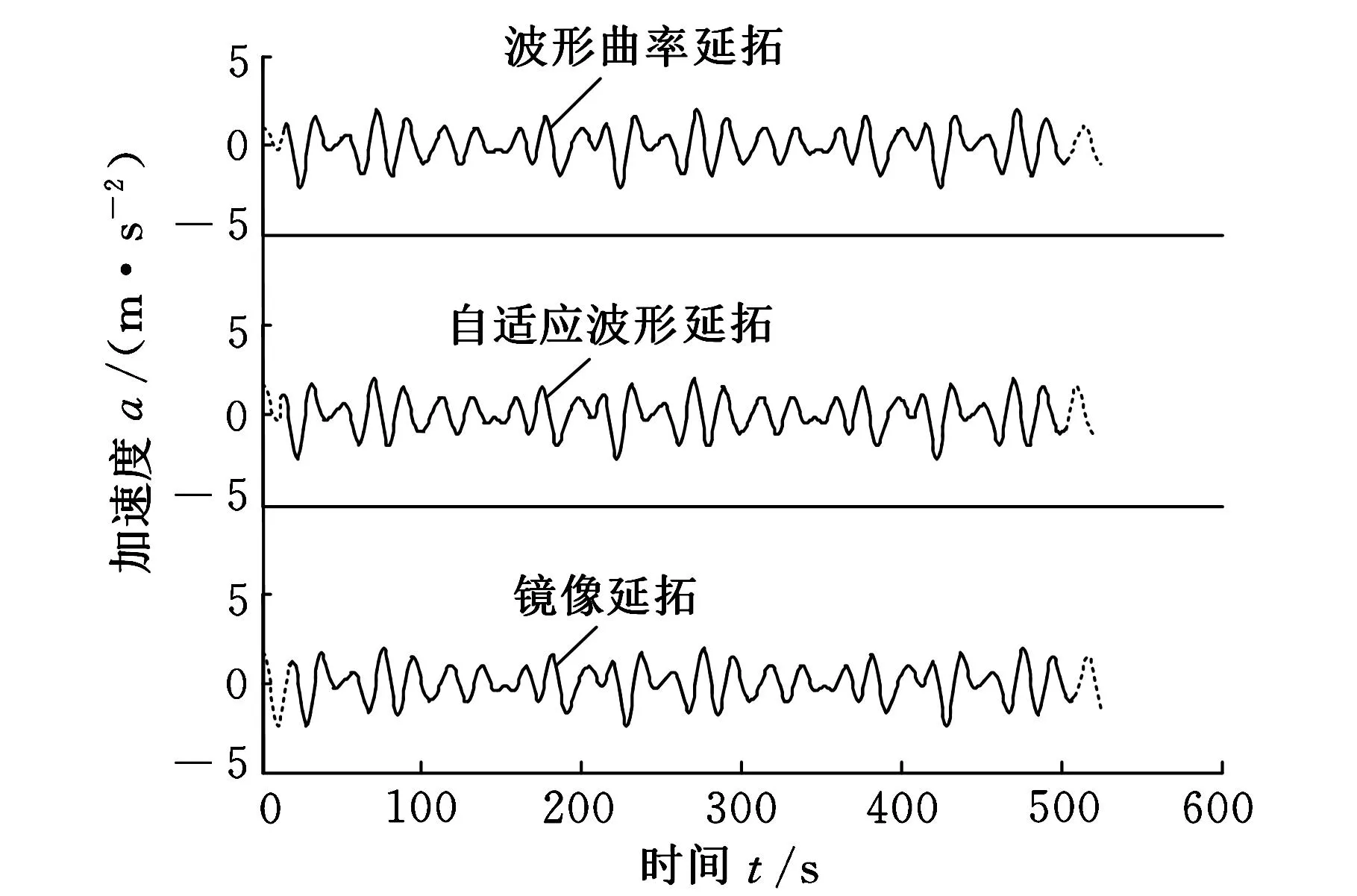
图6　各种延拓方法延拓后的信号

信号经过波形曲率匹配延拓之后的LMD分解结果如图5所示；信号经过自适应波形匹配法、镜像延拓法延拓后的LMD分解结果分别如图7、图8所示；信号未经延拓处理的LMD分解结果如图9所示。

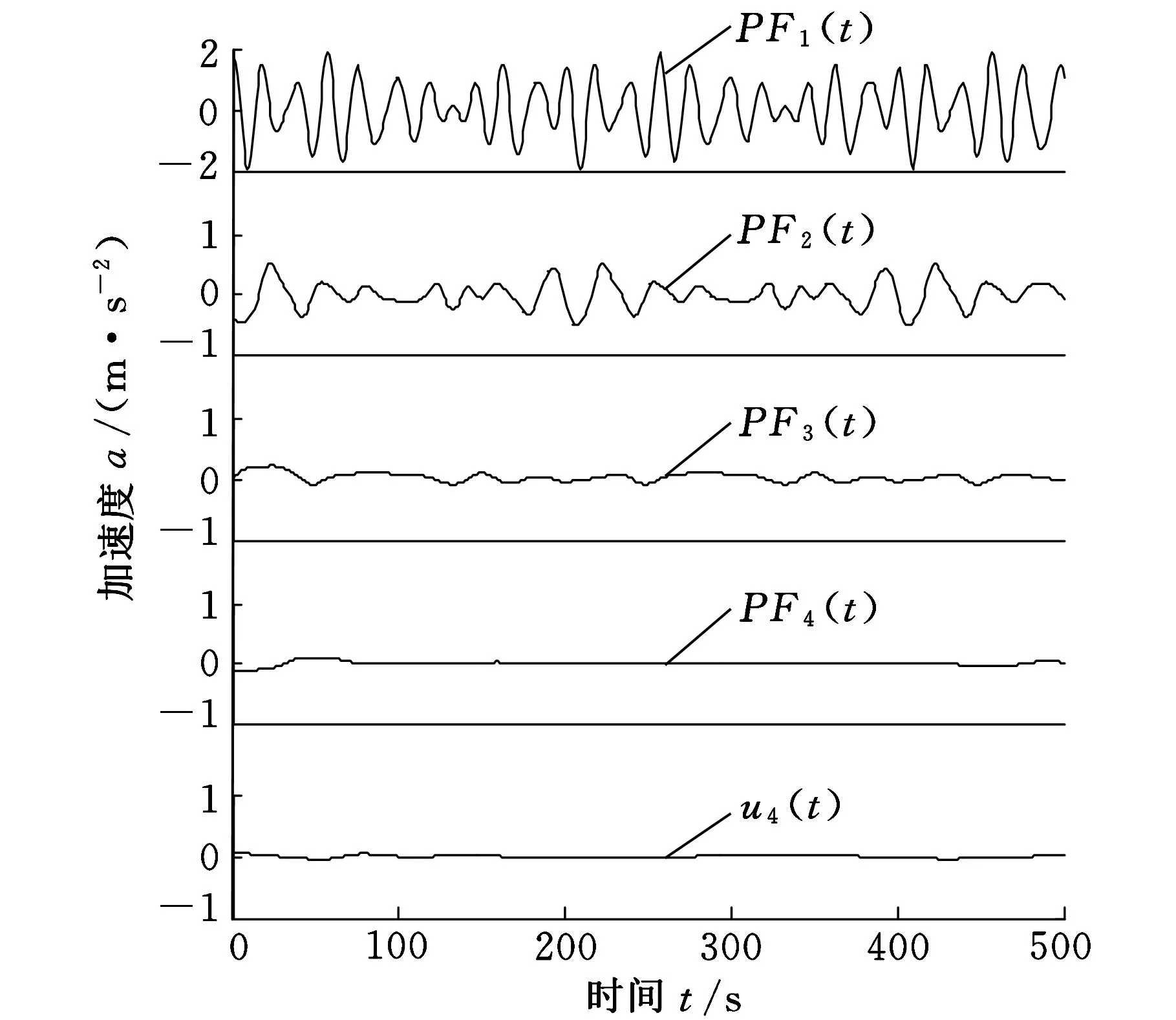
图8　镜像延拓后信号的LMD分解结果

图9　未经延拓信号的LMD分解结果

2.3.2端点效应检测

根据LMD分解结果分别选取各延拓情况下所得的PF分量，将PF分量分别与原始模拟信号x(t)之间进行相关性分析，结果如表1所示。

根据LMD分解理论，原始模拟信号x(t)延拓之后通过LMD分解处理，其主要特征信息集中在前两阶PF分量PF1(t)、PF2(t)中。理论上，前两阶PF分量相关性越大则后两阶PF分量相关性越小，说明延拓效果越好则端点效应影响越小。

表1　各PF分量与原始模拟信号间的相关系数

从表1中的相关性数值能明显看出，经过波形曲率延拓后再进行LMD分解所得的第一阶PF分量PF1(t)与x(t)相关性最大，高达0.963；后两阶PF分量与x(t)相关性非常小，几乎可以忽略，说明波形曲率特征匹配法对端点效应的抑制效果非常显著。

采用文献[5-6]提出的基于能量评价指标检验曲率延拓前后端点效应对乘积函数的影响程度。信号有效值计算公式为

(17)

式中，R为信号的有效值；i为信号序列编号；n为信号长度。

端点效应影响因子θ定义为

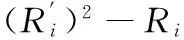
(18)

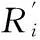
根据θ定义可以得出，端点效应对PF分量影响越小，θ值就越小；如果没有产生端点效应，则θ值为0。相应的θ值结果如表2所示。

表2　延拓前后θ能量表

由表2可以得出结论：相对于其他两种方法，波形曲率匹配延拓对LMD分解中端点效应的抑制效果最好，可以有效提高分解精度。

3工程实验

为进一步验证波形曲率匹配延拓对LMD分解端点效应的改善情况，进行了故障模拟检测实验。试验选取的齿轮箱故障状态是大齿轮点蚀。小齿轮连接电机输入轴，电机轴转动速度为880 r/mim，实验所用减速器大小齿轮齿数分别为75和55。采样频率为51 200 Hz，采样点数为256 000。根据输入轴转速及齿轮参数，计算齿轮理论啮合频率为806.67 Hz，大小齿轮转频分别为10.76 Hz 、14.67 Hz。

对原始数据进行中心化、异常点剔除、小波降噪等一系列预处理，以降低干扰项的干扰，然后进行波形曲率延拓。工程信号数据掺杂其他无关分量较多，虽然周期性明显，但还是会影响延拓结果，所以经过多次试验总结，分别将误差阈值ρ1、ε1设置为0.95、0.01。由于数据较长，故截取左右端部局部信号放大，如图10所示，图中实线为原始信号，虚线为端点延拓部分。

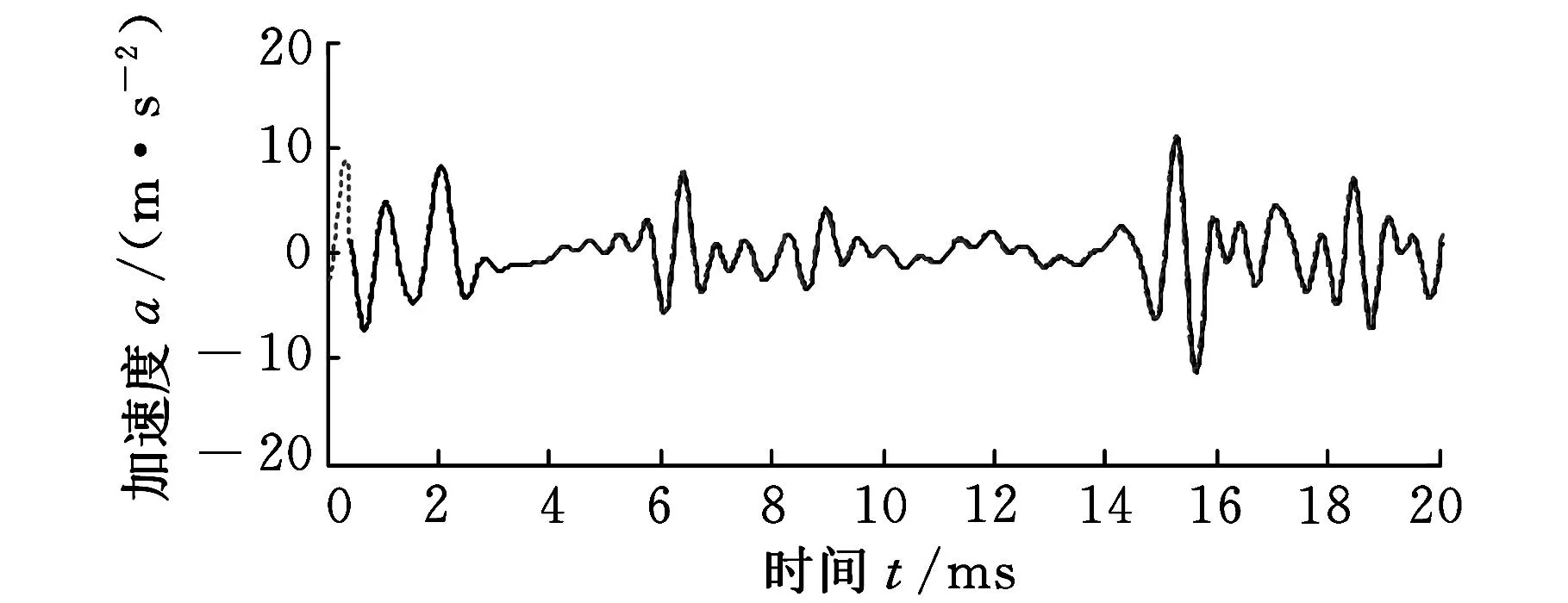
(a)左端点延拓

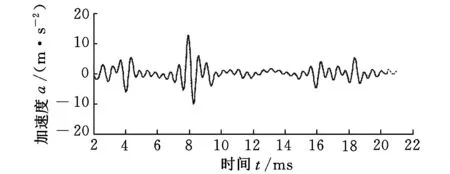
(b)右端点延拓图10　原始信号左右延拓情况

对延拓后的信号及未经波形曲率延拓的信号进行LMD分解，结果如图11、图12所示。

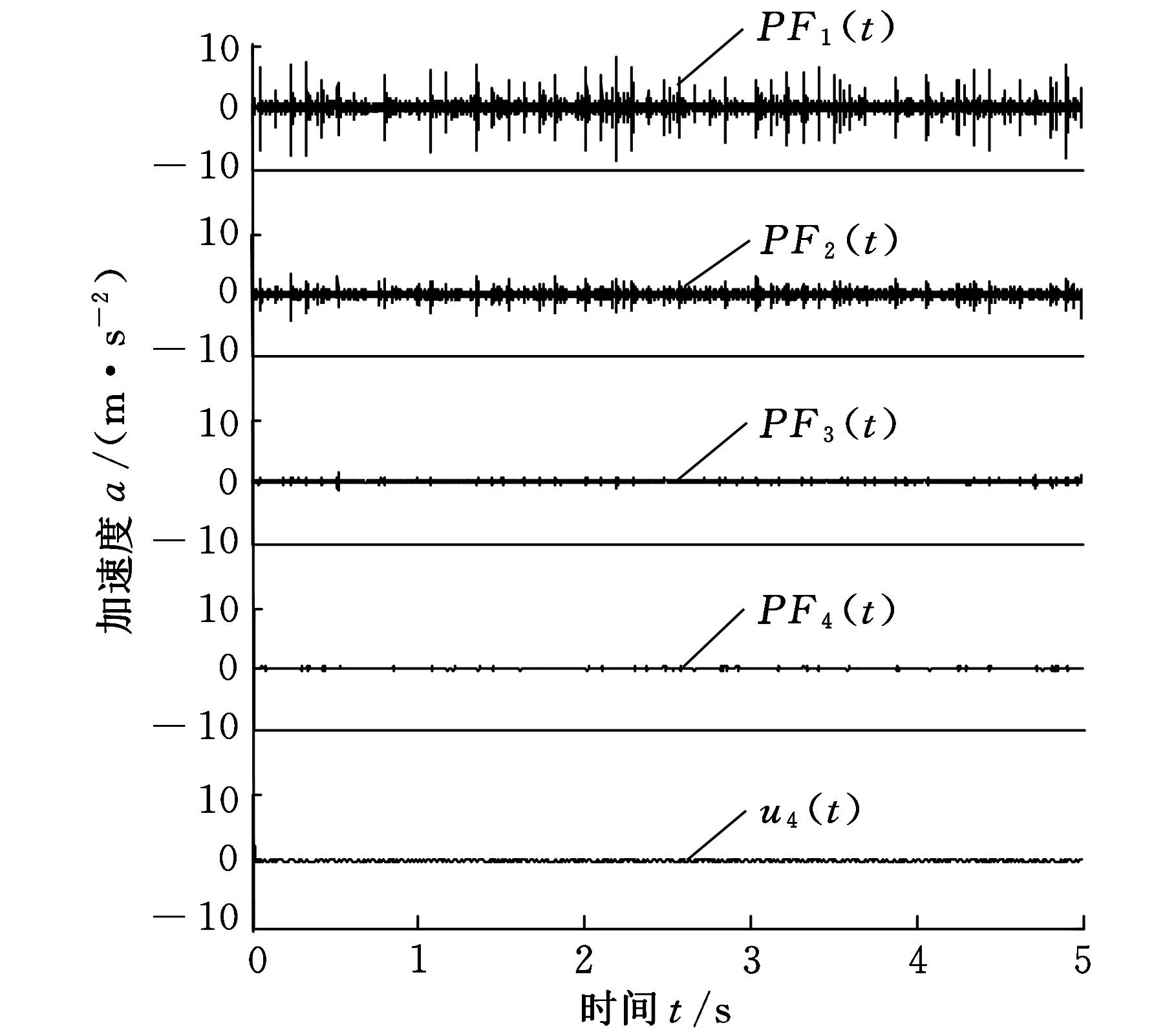
图11　波形曲率延拓后工程信号的LMD分解结果

图12　未经波形曲率延拓工程信号的LMD分解结果

使用相关系数理论方法来计算各个乘积函数与原始信号数据之间的相关情况，结果如表3所示。

表3　各PF分量与原始工程信号之间的相关系数表

由LMD分解原理可知，其分解过程实际上是从高频到低频的“筛选”过程，分解得到的PF分量的频率是由高到低。在所有理论频率中啮合频率及其倍频是最大的，故第一个PF分量PF1(t)对应的是啮合频率及其倍频。由相关系数表可知，信号的主要特征信息集中在第一个PF分量PF1(t)中，故分别选取延拓之前信号及延拓之后信号经LMD分解的第一个PF分量，对其作包络谱分析，结果如图13所示。

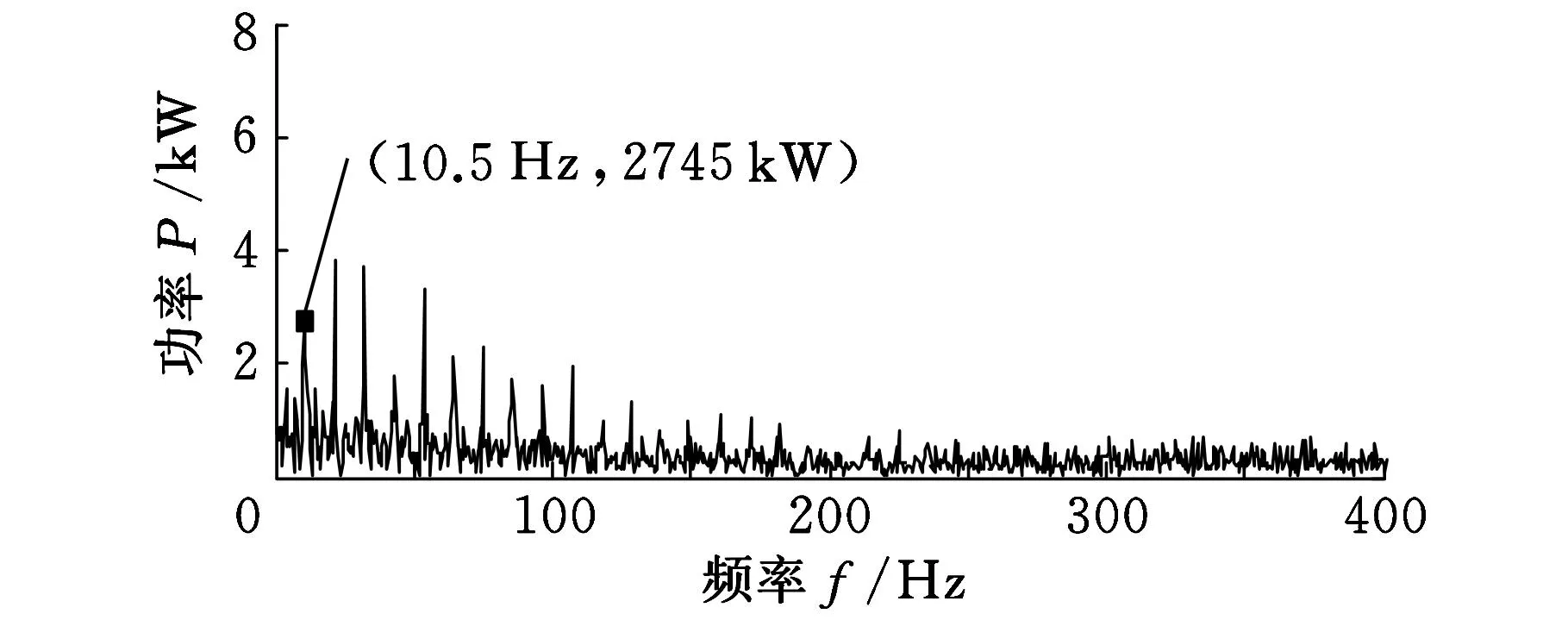
(a)延拓之前

(b)延拓之后图13　延拓前后第一个PF分量PF1(t)的功率谱

由图13可知，对未经延拓的信号和经过延拓之后的信号进行特征信息提取，得到的特征故障频率都能够接近大齿轮的转频10.76 Hz，由此可判断，大齿轮出现故障。但是未经延拓得到的故障调制频率是10.5 Hz，而经过延拓之后得到的故障调制频率是10.75 Hz，相比较而言，10.75 Hz与大齿轮的转频10.76 Hz更加接近，故可以得出结论：经过波形曲率匹配延拓之后的信号能够改善LMD分解过程中的端点效应，提高分解精度，在后续的故障诊断中能够更加精确地提取故障特征。

4总结

根据局域均值分解端点效应产生的原因，提出使用波形曲率匹配延拓方法来从根源上抑制端点效应。波形曲率匹配延拓法基于信号内部的曲率波动来匹配特征波形进行端点延拓，同时设定阈值，提高了匹配精度以及估计精度。通过仿真信号与工程故障齿轮的实验，验证了信号经波形曲率匹配延拓后再进行局域均值分解，能够对端点效应进行有效的抑制。

参考文献：

[1]Smith J S. The Local Mean Decomposition and Its Application to EEG Perception Data[J]. Journal of the Royal Society Interface，2005，2(5)： 443-454．

[2]张亢，程军圣，杨宇．基于自适应波形匹配延拓的局部均值分解端点效应处理方法[J]．中国机械工程，2010，21(4)：457-462．

Zhang Kang, Cheng Junsheng, Yang Yu. Processing Method for End Effects of Local Mean Decomposition Based on Self-adaptive Waveform Matching Extending[J]. China Mechanical Engineering, 2010,21(4): 457-462.

[3]张亢，程军圣，杨宇．局部均值分解方法及其在轴承故障诊断中的应用[J]．中国机械工程，2009，20(22)：2711-2717．

Zhang Kang, Cheng Junsheng, Yang Yu. Local Mean Decomposition Method and Its Application to Roller Bearing Fault Diagnosis[J].China Mechanical Engineering, 2009，20(22)：2711-2717．

[4]程军圣，杨宇，于德介．局部均值分解方法及其在齿轮故障诊断中的应用[J]．振动工程学报，2009，22(1)：76-83．

Cheng Junsheng, Yang Yu, Yu Dejie. Local Mean Decomposition Method and Its Application in Gear Fault Diagnosis Fault Diagnosis[J]. Journal of Vibration Engineering, 2009，22(1)：76-83．

[5]任达千，吴昭同，严拱标．EMD 端点效应的评价指标及抑制端点效应的窗函数法[J]．制造业自动化，2007，29(1)：21-24．

Ren Daqian, Wu Zhaotong, Yan Gongbiao. Evaluation of the EMD End Effect and Its Window Based Method[J]. Manufacturing Automation, 2007，29(1)：21-24．

[6]任达千，杨世锡，吴昭同，等．LMD 时频分析方法的端点效应在旋转机械故障诊断中的影响[J]．中国机械工程，2012，23(8)：951-956．

Ren Daqian, Yang Shixi, Wu Zhaotong,et al. Research on End Effect of LMD Based Time-frequency Analysis in rotating Machinery Fault Diagnosis[J]. China Mechanical Engineering,2012,23(8):951-956．

[7]孟宗，李珊珊，季艳．基于对称差分能量算子解调的局部均值分解端点效应抑制方法[J]．机械工程学报，2014，50(13)：80-87．

Meng Zong, Li Shanshan, Ji Yan. Restraining Method for End Effect of Local Mean Decomposition Based on Energy Operator Demodulation of Symmetrical Differencing[J]. China Mechanical Engineering, 2014，50(13)：80-87．

[8]宁宁，张俊，秦文娟．抑制局域波分解端点效应方法的研究[J]．计算机仿真，2008，25(11)：312-315．

Ning Ning, Zhang Jun, Qin Wenjuan. A Method for Restraining the Ending Effect in Local Wave Method[J]. Computer Simulation, 2008，25(11)：312-315．

(编辑苏卫国)

Waveform Curvature Extension in Applications of Local Mean Decomposition

Wei YongheNiu BaoguoLiu XueliZhao Xuning

Shenyang Ligong University,Shenyang,110159

Abstract:LMD was a kind of signal processing method to self-adaptively decompose the complex amplitude modulation-frequency modulation signals into a series of single-component amplitude modulation-frequency modulation. To some degrees, the decomposition results were of distortions because of the influences of end effects. In order to improve the end effects from LMD, the data segments which were most similar to wave boundary data segments were searched according to the curvature fluctuations of characteristic waves. The waveform curvature was applied in LMD. According to the comparison of mirror extension and self-adaptive waveform match, the advantages of waveform curvature extension were verified. The experiments of simulation signals and actual gear failure were made, the results show that this method can suppress the end effect effectively and improve the decomposition precision.

Key words：local mean decomposition(LMD); end effect; waveform matching;curvature characteristic

收稿日期：2015-08-31

基金项目：国家高技术研究发展计划(863计划)资助项目(2012AA041303)

中图分类号：TH132.4；TH165.3

DOI：10.3969/j.issn.1004-132X.2016.03.011

作者简介：魏永合，男，1971年生。沈阳理工大学机械工程学院教授、博士。研究方向为机械设备的故障诊断、预测和健康管理。牛保国，男，1989年生。沈阳理工大学机械工程学院硕士研究生。刘雪丽，女，1990年生。沈阳理工大学机械工程学院硕士研究生。赵旭宁，女，1990年生。沈阳理工大学机械工程学院硕士研究生。