车辆调度问题的全局
—局部最优信息比粒子群算法研究
朱婷婷,单小红
(桂林电子科技大学 商学院,广西 桂林 541004)
车辆调度问题的全局
—局部最优信息比粒子群算法研究
朱婷婷,单小红
(桂林电子科技大学商学院,广西桂林541004)
[摘要]文章提出了一种新的改进标准粒子群算法即全局—局部最优信息比粒子群算法。该算法与标准粒子群算法和全局—局部最优最小值粒子群优化算法作了比较,仿真实验结果表明,该算法在收敛速度、解的质量和鲁棒性上都表现出了较优的性能,是求解车辆调度问题的一种较好方法。
[关键词]车辆调度问题;粒子群算法;全局—局部最优信息比;数学模型
[DOI]10.13939/j.cnki.zgsc.2016.10.145
1引言
近年来,研究者们先后将一般启发式算法和智能化启发式算法用于车辆调度问题,取得了一些较好的效果。[1]粒子群算法(ParticleSwarmOptimization,PSO)是一种模拟鸟群飞行的仿生算法,有着个体数目少、计算简单、鲁棒性好等优点。[2]
2车辆调度问题(VRP)的描述及数学模型
VRP描述为:有一个配送中心0,配送车辆K辆和货运点个N,每辆车的载重量为qi,各个送货点的需求量为gi,且maxqi≤maxgi,把货物配送到N个送货点,使车辆调度问题的目标函数达到最小。
定义变量如下:
(1)
(2)
cij是配送点之间的距离,则VRP的数学模型表示为:
(3)
(4)
(5)
(6)
(7)
xijk=0或1, i, j=1, 2, …, N; k=1, 2, …, K
(8)
yik=0或1, i, j=1, 2, …, N; k=1, 2, …, K
(9)
X=(xijk)∈S
(10)
式(3)为目标函数:车辆行驶的总路径最小;式(4):每条线路上配送点需求量之和不超过最大载重量;式(5):每个配送点仅被访问一次;式(6)(7):每个送货点的需求量只能由一辆车完成;式(8)(9):变量取值范围;式(10):支路消去约束。该问题在约束条件下,使所有车辆的总路径最小。
3粒子群算法及其改进
3.1粒子群算法
PSO算法初始化粒子群,在迭代过程中,粒子将跟踪个体极值pbest和全局极值gbest来更新下一时刻的位置,设搜索空间为D维,总粒子数为n,粒子i在t时刻的位置为:
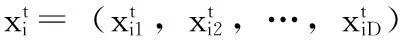
粒子在t+1时刻的位置通过下式进行更新:
(11)
(12)
c1和c2代表学习因子;r1和r2为均匀分布在(0,1)区间的随机数;第d维的位置取值范围为[-xmax,xmax],速度的取值范围为[-vmax, vmax];w代表惯性权重,令w=初始w-当前迭代次数(初始w-终止w)/最大迭代次数,最后得到的gbes就是粒子群算法的最优解。
3.2改进的粒子群算法
粒子群算法参数的设置对算法的寻优性能起着重要的作用。全局—局部最优最小值粒子群算法(GLBest-PSO)对标准PSO进行了改进,即:
(13)
(14)
受到GLBest-PSO的启发,本文构造了全局-局部最优信息比粒子群算法(Global-LocalOptimalInformationRatioParticleSwarmOptimization,GLIR-PSO),原速度更新公式(11)改进为:
(15)
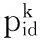
4车辆调度问题的GLIR-PSO算法
4.1问题的编码与解码
实现该算法的关键问题之一是找到一种合适的表达方法,使粒子与解对应。本文根据文献[3]的思路,将车辆和对应的送货点的顺序表示出来。对于N个送货点的VRP问题,每个送货点对应两个属性:完成该配送任务的车辆号k和在车辆中的配送顺序r,每个粒子对应的2N维向量被分解为两个N维向量:Xk和Xr,其中Xk表示各配送点的车辆编号,Xr表示各配送点对应的配送顺序。速度向量V对应的被分解为Vk和Vr。
假设有7个送货点的VRP问题,所需车辆数为3,编码过程如表1所示。

表1 粒子编码过程
将表1粒子的状态对应为配送方案[4]为:
车辆1:0→1→0
车辆2:0→4→5→3→2→0
车辆3:0→7→6→0
这种编码方式使得每个配送点都能得到服务并且每个送货点的需求量只能由一辆车完成,粒子更新的方式简单、易懂,求解过程的计算量大大减少。
4.2GLIR-PSO算法实现过程
粒子群算法的具体实现步骤如下:
步骤1:初始化粒子群。
①初始化种群规模P,粒子维数2N,w,c1,c2,最大迭代次数Loop count;
②初始化Xk和Xr,使其分别属于1~K的随机整数和1~L的随机实数;初始化Vk和Vr的分量,使其分别属于-(K-1)~(K-1)的随机整数和-(L-1)~(L-1)的随机实数;
③用评价函数Eval评价所有粒子的适应度,若不满足约束条件则令f=fmax,fmax是一个很大的数;
④初始评价值作为每个粒子的局部极值,最优的初始评价值作为全局极值。
步骤2:更新位置、速度,并输出优化结果。
①按式(15)计算Vk和Vr,按式(12)计算Xk和Xr,如果超过边界值则取边界值;
②用Eval评价所有粒子的适应度;
③更新局部极值和全局极值,若某粒子当前的位置优于pbest,则更新pbest,若粒子群的当前位置优于gbest,则更新gbest;
④若满足终止条件,输出gbest;否则返回①。
5仿真实验结果与分析
现有一个配送中心,7个送货点,设所有车辆的最大装载量为1t,需求量矩阵为P=[0.89,0.14,0.28,0.33,0.21,0.41,0.57],距离矩阵如表2所示。
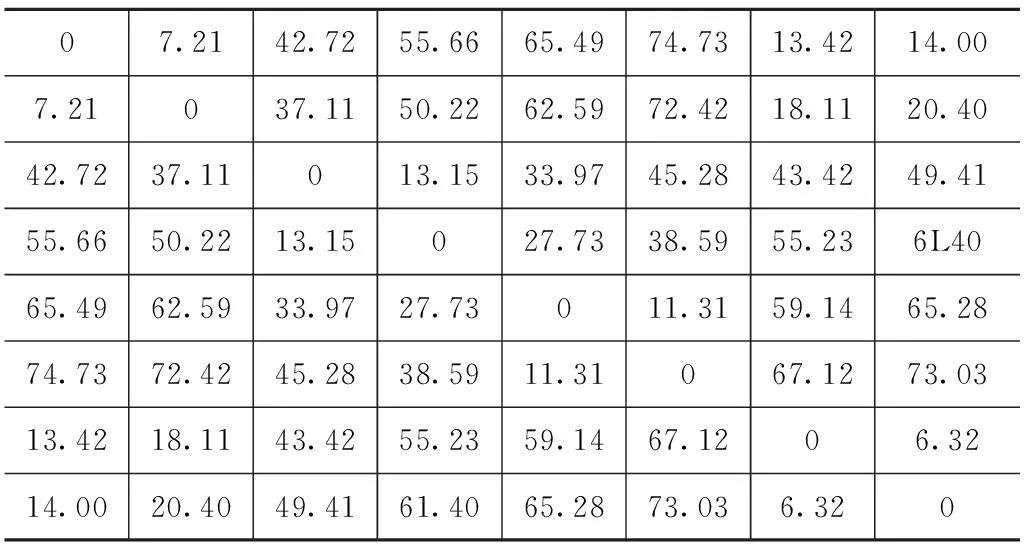
表2 距离矩阵
使用Matlab7.0编程,参数设置:P=30,2N=14,wstar=0.9,wend=0.4,c1=c2=2,Loopcount=500,惩罚因子R=100000,最终由3辆车完成配送任务,并且最短总路径为217.81。车辆最优调度方案如表3所示。
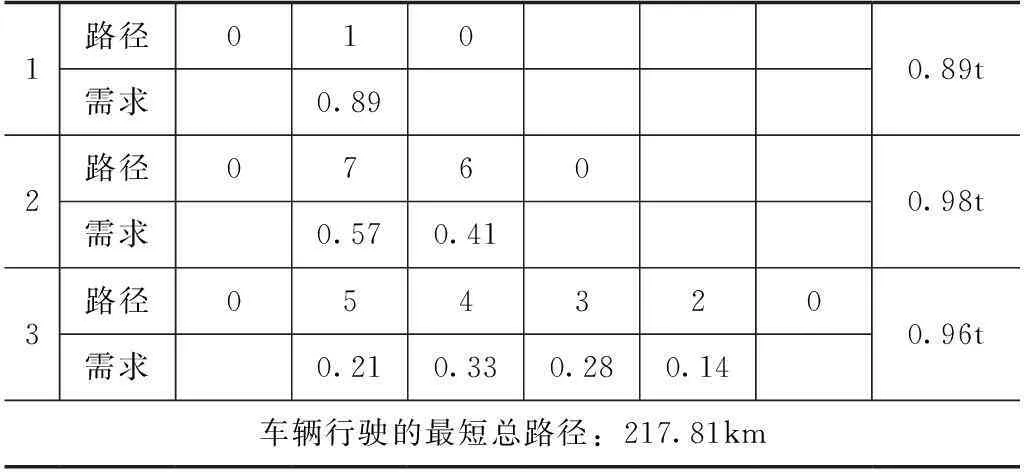
表3 车辆最优调度方案
本文将 GLIR-PSO算法与BPSO和GLBest-PSO进行仿真实验,并对优化结果进行比较。每种算法依次运行20次,其中,GLIR-PSO有13次搜索到最优解,而BPSO和GLBest-PSO分别只有11次和10次,并且GLIR-PSO的20次实验平均路径252.73km优于BPSO和GLBest-PSO算法所得结果(304.96km和276.44km),说明GLIR-PSO算法解的质量在一定程度上得到了提高,收敛速度变快。
在20次实验中,GLIR-PSO的最短路径的方差小于BPSO和GLBest-PSO算法所得结果(137.12645和86.28476),其最短路径的方差为61.11745,比BPSO和GLBest-PSO算法的结果小55.4%和29.2%,所以GLIR-PSO算法在解的鲁棒性上表现出了较优的性能。以上结论在表4中显示:
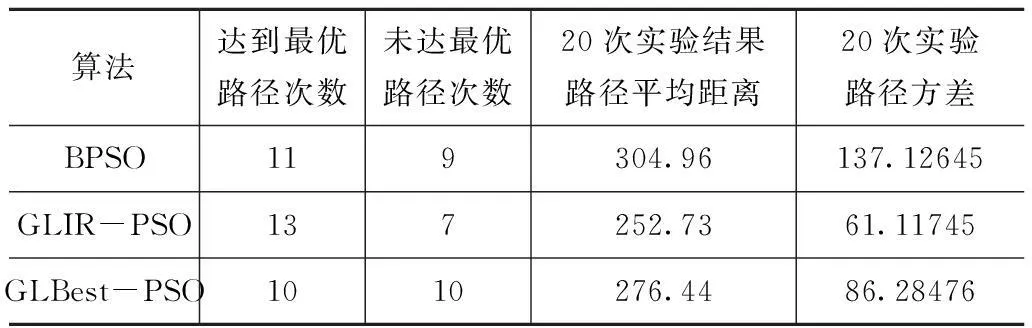
表4 优化结果对比
通过上述仿真实验有效地验证了这种新的改进算法——GLIR-PSO算法,有效地避免了标准粒子群算法的“趋同性”,确保正确的搜索方向,且持续地找到全局最优解。
6结论
目前,虽然车辆调度系统已在国内一些领域得到初步应用,但发展很不成熟,存在算法复杂和运行不稳定等缺陷,针对此现状,本文提出一种新型的GLIR-PSO算法以有效提高车辆调度系统运行的效率性和稳定性,将全局和局部最优信息比引入到算法的更新过程,来对标准粒子群算法进行有效改进,该新型算法有效克服了早熟收敛现象,在收敛速度、解的质量和鲁棒性上都表现出了较优的性能。
参考文献:
[1]李军,郭耀煌.物流配送车辆优化调度理论与方法[M].北京: 中国物资出版社,2001:76-77.
[2]Kennedy J,Eberhart R C.Particle swarm optimization[C]//Proc.IEEE international conference on neural networks,IV.Piscataway,NJ: IEEE service center,1995: 1942-1948.
[3]Salmen A,Ahmad I,Al-Madani S.Particle swarm optimization for task assignment problem[J].Microprocessors and microsystems,2002(26): 367-371.
[4]李宁,邹彤,孙德宝.带时间窗车辆路径问题的粒子群算法[J].系统工程理论与实践,2004,4(4): 130-135.
[基金项目]国家自然科学基金资助项目(项目编号:71162017);广西自然科学基金资助项目(项目编号:2011GXNSFB018061);桂林电子科技大学研究生教育创新计划资助项目(项目编号:GDYCSZ201438)。
[作者简介]朱婷婷(1987—),女,河南信阳人,桂林电子科技大学硕士研究生。研究方向:物流管理与运作;单小红(1989—),女,江西上饶人,桂林电子科技大学硕士研究生。研究方向:物流管理与运作。

