对流边界层湍流通量及逆梯度输送参数化分析

韩永翔,宋昊冬*,刘烽,赵天良

① 南京信息工程大学 气象灾害预报预警与评估协同创新中心,江苏 南京 210044;② 南京信息工程大学 中国气象局气溶胶与云降水重点开放实验室,江苏 南京 210044

对流边界层湍流通量及逆梯度输送参数化分析

韩永翔①②,宋昊冬①②*,刘烽①②,赵天良①②

① 南京信息工程大学 气象灾害预报预警与评估协同创新中心,江苏 南京 210044;② 南京信息工程大学 中国气象局气溶胶与云降水重点开放实验室,江苏 南京 210044

2013-05-10收稿,2015-06-11接受

国家自然科学基金资助项目(41075113;41175093);南京信息工程大学引进人才启动资助项目(20110304)

摘要“K”理论是众多气象预报模式中运用最广泛的湍流参数化方案之一,但无法解释“逆梯度”的输送,必须进行修正。最具代表性的修正方案有三种:方案Ⅰ(Deardroff方案)、方案Ⅱ(Holtslag和Moeng方案)和方案Ⅲ(刘烽方案)。本文利用香河的边界层观测资料对上述三种方案进行验证和比较,发现方案Ⅰ的结果在整个对流边界层(Convective Boundary Layer,CBL)呈系统性偏低,与观测不符;方案Ⅱ在CBL中上部能够再现逆梯度输送现象,基本能给出合理的湍流通量垂直分布,但在CBL的下部和上部与观测不符;方案Ⅲ的逆梯度项与高度有关,并在CBL中部达到最大,而其他两个方案中逆梯度项随高度不变。该方案不但在CBL中上部与方案Ⅱ的结果一致,并能合理表达整个CBL内的湍流通量分布,更接近观测结果。

关键词

对流边界层

湍流通量

参数化

逆梯度

输送

目前各种尺度的数值气象预报模式和空气质量预报模式,都无法分辨出小于模式网格尺度的边界层湍涡,如要定量求解边界层内部的热量、水汽和污染物的传输,必须要对湍流通量进行参数化(郭光等,1992;张燕和徐玉貌,2002;周德刚等,2012),即需要一个针对湍流封闭问题的解决方案。“K”理论就是一个表述一阶湍流封闭通量和梯度关系的解决方案,因其表述简单,已被成功运用于气候和气象预报模式中,是目前运用最广泛的湍流参数化方案之一。同时,运用于各种大气污染与气候模式中的一阶半闭合(如k-ε或k-e闭合)及理论研究中的二阶、三阶等高阶闭合中,其更高阶矩湍流输送项的参数化仍以“K”理论为基础,但“K”理论的最大缺陷是无法解释“逆梯度”的输送现象。在以热力主导的对流边界层中上部,热量通量可突破温度梯度的束缚,从温度低的区域向温度高的区域输送;或者仅有很小的温度梯度,仍有显著的热流存在。这两种现象即“逆梯度”输送。早在20世纪50和60年代的野外观测就发现“逆梯度”的存在,如Bunker(1956)利用飞机观测到在大西洋上空150～550 m的高度范围内,温度梯度是正值,而热量仍向上传输。随后Lettau and Davidson(1957)在观测过程中发现在距离地面100 m高度处存在逆梯度输送的热流量。Telford and Warner(1964)在观测中两次发现了逆梯度传输的热量流,其高度分别为150～350 m和150～1 250 m之间。最近的关于逆梯度输送的观测报道来自WL-ARPDD94实验资料的分析(Qian et al.,2000)。

因为对流层上部的位温梯度非常小,如果继续使用“K”理论,湍流热扩散系数必须为负值,这与基于分子扩散理论建立的通量梯度关系相违背。因此,必须对“K”理论进行修正。最具代表性的“K”理论修正方案来自Deardorff(1972)、Holtslag and Moeng(1991),二者都在湍流闭合方案中引入了“逆梯度”项,但他们基于不同的湍流物理过程来导出“逆梯度”项,故而对逆梯度现象的物理解释也就不同。Deardorff认为逆梯度效应来源于热浮力项,而Holtslag and Moeng则认为逆梯度效应来源于湍流输送项,该论点被大家所普遍接受(Cheng et al.,2002;De Roode et al.,2004)。刘烽和毕雪岩(2000)、刘烽(2001)则认为逆梯度项是由湍流时间尺度、湍流强度以及平均场的空间非均匀性共同决定,与湍流输送项和热浮力并无显含关系。显然,这三种“K”理论修正方案中关于逆梯度项的来源具有完全不同的解释,哪一个更符合实际呢?目前没有任何有关这方面的工作。

由于湍流物理量观测资料极端缺乏,用外场实验观测资料进行边界层中逆梯度输送的研究极为罕见,对其分析和验证主要借助于大涡模拟来进行(Cheng et al.,2002;De Roode et al.,2004)。众所周知,数值模拟尽管能够给边界层涡动力学提供洞察力,但仍无法代替实际观测。因而,用实际的外场观测资料进行边界层逆梯度输送的研究更为重要。本文利用WL-ARPDD94在北京香河的实验资料对Deardorff方案(简称方案Ⅰ),Holtslag and Moeng方案(简称方案Ⅱ)以及刘烽方案(简称方案Ⅲ)进行对比,分析其在实际运用中的表现,进而探讨逆梯度传输的实质原因,寻找普适的湍流方案。对这一科学问题的研究,将有助于提出更为合理的湍流参数方案,增加对边界层污染物扩散和传输过程的认识,为进一步发展湍流闭合方案提供科学依据。

1湍流参数化方案和资料简介

经典的湍流参数化方法是基于混合长理论,其假设湍流动量交换与分子粘性引起的动量交换在形式上相似。因此,在分子运动论中,分子粘性切应力τ′为:

(1)

(2)

由以上方程可得:

(3)

同样对于热力湍流通量可得:

(4)

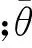
(5)

其中,γθ称为逆梯度项。

假设水平均匀和Boussinesq近似的条件下,湍流热量通量方程表达如下(Deardorff,1972):

(6)

Deardroff(1972)忽略湍流输送项(即方程(6)右端第一项)并认为对流边界层中的逆梯度是由于热浮力引起的,得到湍流闭合方案(即方案Ⅰ)如下:

(7)

(8)

其中,τD为与湍能和混合长有关的时间尺度。

Holtslag and Moeng(1991)通过利用大涡模拟的结果,发现湍流输送项不能够忽略,并给出一个准定常条件下湍流输送项与压力脉动贡献的经验参数化公式:

(9)

其中,w*为对流速度尺度;θ*为对流温度尺度;τi为各向同性下的时间尺度;zi为对流边界层高度;α、b分别为常数1/2、2。

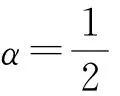
(10)

(11)

方案Ⅲ基于混合长理论,并在保留高阶项后,得到湍流通量分布为:

(12)

因此有:

局地顺梯度:Kh=l|w′|。

(13)

(14)

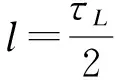
则有:

(15)

(16)

(17)

(18)

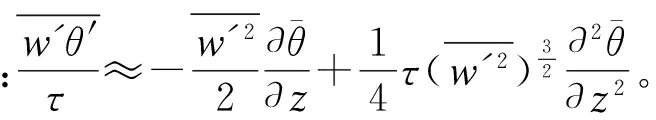
(19)

本文所用的观测数据来源于WL-ARPDD94外场实验计划(Qian et al.,2000)。该实验于1994年8月15日起在北京香河实验区(116°59′E,39°40′N)实施,历时1个月,其科学目的是研究边界层结构的动力和热力学特征,处理后的资料满足大气边界层基本热力特征研究。基于观测资料和现有湍流理论,Qian et al.(2000)给出了以下主要关系:

(20)

由上可得:

(21)

此外,由香河实验资料拟合得到的归一化垂直速度方差:

(22)

这和前人空气质量输送实验(Air Mass Transformation EXperiment,AMTEX)的结果非常相近(Lenschow et al.,1980):

(23)

表1香河边界层实验观测参数(Qian et al.,2000)

Table 1Boundary layer parameters in Xianghe(Qian et al.,2000)

时间zi/mU12/(m·s-1)u*/(m·s-1)w*/(m·s-1)θ*/Kw'θ'0/(K·m·s-1·10-3)τi/s1994-08-25T11:305101.00.090.920.50462791994-08-25T12:305101.40.120.900.49442831994-08-25T13:304801.80.140.860.48412781994-08-30T12:304502.00.140.960.63602351994-09-05T11:006002.60.131.060.57602841994-09-05T15:006602.80.470.950.42403471994-09-07T10:004802.20.220.820.43352931994-09-07T10:303902.50.350.870.59512251994-09-07T12:007202.50.331.040.46483461994-09-07T12:306202.40.361.000.4949311

2三种方案的热通量计算结果与分析

利用在香河所获得10个对流边界层过程的垂直廓线资料,对方程(17—19)逐一计算3个方案的湍流热通量。

由于直接观测的位温脉动方差资料不能直接利用方程(17),必须找出热浮力与垂直速度方差的关系。在计算方案Ⅰ的湍流热通量时,根据逆梯度效应来源于热浮力项(机械产生项以及湍流输送项忽略不计)的假设条件,利用Coulter and Wesely(1980)提出一个关于热浮力与垂直速度方差简化关系来估计热力混合边界层的热通量随高度的变化。其热浮力与垂直速度方差简化方程为:

(24)

(25)

方案Ⅱ提出在边界层中部的湍涡时间尺度可由下式给出:τ=0.50 zi/w*,最大的湍涡可以达到混合层高度。

方案Ⅲ认为时间尺度与含能涡的大小有关,所以随高度发生变化。在CBL中上部的湍涡明显要大于近地层小湍涡,那里有足够大的含能涡可以实现非局地逆梯度输送,这种关系可以从方案Ⅲ(方程(19))中看出。

图1为3个方案计算出的10个独立观测个例的顺梯度、逆梯度以及总的通量结果。由图1可见,在热浮力为逆梯度来源的假设条件下,利用方程(24、25)可得到逆梯度项,在每个个例中所得结果都非常一致(见图1中粉红和绿色虚线),证明用这种方法求取的逆梯度是可信的。此外,方案Ⅰ估计的湍流通量普遍偏低(见图1中FL-D黑色虚线),而方案Ⅱ、Ⅲ接近于观测结果。因此,下文重点讨论和比较方案Ⅱ和Ⅲ的结果。

10个个例中(图1a—j表示个例a—j),发现有4个(个例d、e、i和j)方案Ⅲ的湍流通量在整个CBL内小于方案Ⅱ的结果。其他个例中用两种方案所计算的湍流通量垂直分布则有所差异,如个例a,方案Ⅱ和Ⅲ在无量纲高度0.35以上基本吻合,0.35以下,方案Ⅲ小于方案Ⅱ;个例b,方案Ⅲ首先在底部小于Ⅱ,然后趋于一致,并在0.45高度以后大于方案Ⅱ,但在CBL上部与Ⅱ再次吻合;个例c,在CBL底部,方案Ⅲ小于Ⅱ,但在0.2高度以上,均大于方案Ⅲ的结果;个例f,方案Ⅲ首先小于Ⅱ,在中部0.55吻合,以后略微小于方案Ⅱ;个例g,在0.2高度以下相同,0.2以上,方案Ⅲ总是大于Ⅱ;个例h,其湍流通量较其他个例大,方案Ⅲ在0.25高度以上大于方案Ⅱ。

由于顺梯度分量在三个方案中相同,因此逆梯度分量的贡献决定了湍流通量的差异,逆梯度项达到一致时,后两个方案结果相等或差异极小。

图1　平均湍流热通量除以时间尺度随无量纲高度的变化(蓝色实线表示顺梯度输送的湍流通量分量(DG);粉红色虚线、实线和点画线分别表示方案Ⅰ(CG-D)、Ⅱ(CG-H)和Ⅲ(CG-L)中逆梯度输送引起的湍流通量分量;绿色虚线表示方案Ⅰ(CG-D)的参考值;黑色虚线、实线和点画线分别表示方案Ⅰ(FL-D)、Ⅱ(FL-H)和Ⅲ(FL-L)的湍流热通量)Fig.1　Vertical profiles of turbulent heat flux divided by the time scale with dimensionless (the solid lines in blue represent the turbulent flux component due to local or downward gradient transport(DG);the dotted,solid,and dashed-dotted lines in pink denote the turbulent heat flux component caused by the counter-gradient term in scheme Ⅰ(CG-D),Ⅱ(CG-H) and Ⅲ(CG-L),respectively;the green dotted line is the reference of the counter-gradient term for scheme Ⅰ(CG-D);the dotted,solid and dashed-dotted lines in black represent the turbulent heat flux calculated by scheme Ⅰ(FL-D),Ⅱ(FL-H) and Ⅲ(FL-L),respectively)

图2　平均湍流热通量除以时间尺度随无量纲高度的变化(10个CBL个例的平均廓线;蓝色实线表示顺梯度输送的湍流通量分量(DG);粉红色虚线、实线和点画线分别表示方案Ⅰ(CG-D)、Ⅱ(CG-H)和Ⅲ(CG-L)中逆梯度输送引起的湍流通量分量;绿色虚线表示方案Ⅰ(CG-D)的参考值;黑色虚线、实线和点画线分别表示方案Ⅰ(FL-D)、Ⅱ(FL-H)和Ⅲ(FL-L)的湍流热通量)Fig.2　Vertical profile of averaged turbulent heat flux divided by the time as a function of dimensionless (the results are averaged over 10 CBL cases from datasets at Xianghe;the solid lines in blue represent the turbulent flux component due to local or downward gradient transport(DG);the dotted,solid,and dashed-dotted lines in pink denote the turbulent heat flux component caused by the counter-gradient term in scheme Ⅰ(CG-D),Ⅱ(CG-H) and Ⅲ(CG-L),respectively;the green dotted line is the reference of the counter-gradient term for scheme Ⅰ(CG-D);the dotted,solid and dashed-dotted lines in black represent the turbulent heat flux calculated by scheme Ⅰ(FL-D),Ⅱ(FL-H) and Ⅲ(FL-L),respectively)

为了更清楚地看出二者的差异,本文计算了10个个例的湍流通量平均值(图2)。可见,方案Ⅱ和Ⅲ仅仅在CBL中部(0.45～0.65)相吻合。在下部和上部,方案Ⅲ的结果均低于方案Ⅱ,二者之差的绝对值下部大于上部。对比Qian et al.(2000)给出的更多个例的观测以及方案Ⅱ计算结果的平均廓线,发现观测值在中部与计算结果一致,而在下部与上部均小于方案Ⅱ的计算值,这与由方案Ⅲ的通量廓线行为非常一致,因此方案Ⅲ更接近观测事实。

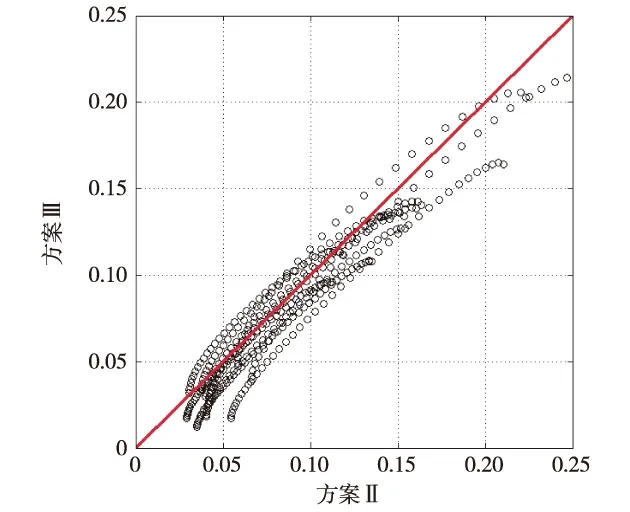
图3　方案Ⅱ和Ⅲ湍流热通量计算值的相关点聚图Fig.3　Scatter plot showing the relationship of turbulent heat fluxes between scheme Ⅱ and scheme Ⅲ

图4　平均湍流热通量除以时间尺度随无量纲高度在整个CBL中的变化(蓝色实线表示顺梯度输送的湍流通量分量(DG);粉红色虚线、实线和点画线分别表示方案Ⅰ(CG-D)、Ⅱ(CG-H)和Ⅲ(CG-L)中逆梯度输送引起的湍流通量分量;绿色虚线表示方案Ⅰ(CG-D)的参考值;黑色虚线、实线和点画线分别表示方案Ⅰ(FL-D)、Ⅱ(FL-H)和Ⅲ(FL-L)的湍流热通量)Fig.4　Vertical profile of averaged turbulent heat flux divided by the time as a function of the full range of within the CBL(the solid lines in blue represent the turbulent flux component due to local or downward gradient transport(DG);the dotted,solid,and dashed-dotted lines in pink denote the turbulent heat flux component caused by the counter-gradient term in scheme Ⅰ(CG-D),Ⅱ(CG-H) and Ⅲ(CG-L),respectively;the green dotted line is the reference of the counter-gradient term for scheme Ⅰ(CG-D);the dotted,solid and dashed-dotted lines in black represent the turbulent heat flux calculated by scheme Ⅰ(FL-D),Ⅱ(FL-H) and Ⅲ(FL-L),respectively)

方案Ⅲ的理论也可以解释为何优于方案Ⅰ和Ⅱ,且与观测事实相符。其理论核心认为逆梯度项应该与湍涡尺度随高度的变化有关。在边界层下层主要以由风切变造成的小尺度机械湍流为主,而中上部以热力湍流造成的大尺度湍涡为主,其非局地特征是造成逆梯度输送的主要原因。虽然逆梯度项本身的值一般在对流边界层中部达到最大值,然后随高度减少(与温度随高度的二阶导数有关),在CBL的上半部分随着局地梯度项(与温度随高度的一阶导数成正比)贡献的增加和逆梯度项的迅速减弱,其综合结果使得向上的热通量减弱和消失,甚至转为向下的热通量。所以逆梯度效应并未出现在对流边界层的顶部而在对流层中上部,那里的温度梯度值非常小并几乎为零,但显著的热量传输仍然存在(即逆梯度项的作用),所以方案Ⅲ值与观测事实相符合。

3三种方案物理基础回顾与讨论

存在时,方案Ⅰ退化为传统的一阶封闭。

方案Ⅲ从基本的混合长理论出发,保留二级近似而非传统的一级近似,从数学上讲,物理变量对空间的二阶导数说明某点湍流物理量的变化不但取决于局地变化而且与其周围其他点上的变化有关,这就是所谓的非局地效应。方案Ⅲ并未强调湍流逆梯度来源,而是由湍流强度、时间尺度以及空间非均匀性决定。无论是热力湍流或是机械湍流,均以其时间尺度和强度等基本量决定逆梯度的大小和湍涡尺度在垂直空间上的变化,湍涡尺度随高度的变化使得逆梯度项的贡献随高度发生变化而非一个常数。目前普遍认为,逆梯度传输是由大湍涡作用产生的现象,在CBL中上层以热力湍流造成的大尺度湍涡为主,而在边界层底部主要以小尺度机械湍流为主。方案Ⅲ不再强调逆梯度输送是由热浮力产生或湍流输送项引起,而认为逆梯度输送可能就是湍流本身的一种属性。因此,方案Ⅲ不仅适合于CBL而且能同时满足稳定边界层,使后者中的逆梯度项自动失去控制效应。因此,方案Ⅲ的湍流方案无需以边界层的热力稳定性为前提,可视为一种普适的湍流方案,为建立一个统一的、适应于任何标量物质在湍流环境中的扩散、迁移等参数化方案提供了新的思路。此外,在本文个例分析中也可以看出,延伸至其他参数化方案以外的CBL区域,方案Ⅲ同样可以给出合理的结果。

4结论

本文利用香河地区的实验数据对三种湍流参数化方案作了对比和分析,结果发现:

1)方案Ⅰ估算的湍流通量在整个CBL中系统偏低。

2)方案Ⅱ在边界层中部与观测结果一致,但在CBL下部和上部均估计过高。

3)方案Ⅲ在整层CBL中与观测结果一致,其估算结果在下部和上部均小于方案Ⅱ的结果。在到达向一个稳定层过度的CBL顶端和超绝热底部,仅方案Ⅲ能给出合理的分布。方案Ⅲ从理论和个例分析中能更好地反映和解释CBL热量传输机制以及逆梯度的传输现象,并可用于整个CBL。

本文仅仅利用了香河地区的实验数据,比较和分析了三个方案的结果,但其结论是否具有普适性仍需要更多的观测数据来支持和验证。

参考文献(References)

Blackadar A K.1997.Turbulence and diffusion in the atmosphere[M].Berlin:Springer.

Bunker A F.1956.Measurements of counter-gradient heat flux in the atmosphere[J].Aust J Phys,9(1):133-143.

Cheng Y,Canuto V M,Howard A M.2002.An improved model for the turbulent PBL[J].J Atmos Sci,59(9):1550-1565.

Coulter R L,Wesely M L.1980.Estimates of surface heat flux from sodar and laser scintillation measurements in the unstable boundary layer[J].Journal of Applied Meteorology,19(10):1209-1222.

Deardroff J W.1972.Theoretical expression for the counter-gradient vertical heat flux[J].J Geophys Res,77(30):5900-5904.

De Roode S R,Duynkerke P G,Jonker H J J.2004.Large eddy simulation:How large is large enough?[J].J Atmos Sci,61(4):403-421.

郭光,严绍瑾,张培昌.1992.大气边界层湍流的混沌特性[J].南京气象学院学报,15(4):476-484.Guo G,Yan S J,Zhang P C.1992.The chaotic characteristics of the atmospheric boundary layer turbulence[J].J Nanjing Inst Meteor,15(4):476-484.(in Chinese).

Holtslag A A M,Moeng C H.1991.Eddy diffusivity and countergradient transport in the convective atmospheric boundary layer[J].J Atmos Sci,48(14):1690-1698.

Lenschow D H,Wyngaard J C,Pennell W T.1980.Mean-field and second-moment budgets in a baroclinic,convective boundary layer[J].J Atmos Sci,37(6):1313-1326.

Lettau H H,Davidson B.1957.Exploring the atmosphere’s first mile[M].London:Pergamon Press.

刘烽.2001.逆梯度输运与大气边界层湍流参数化研究[D].青岛:青岛海洋大学.Liu F.2001.A study of counter gradient transport and turbulent paramerization in atmospheric boundary layer[D].Qingdao:Ocean University of Qingdao.(in Chinese).

刘烽,毕雪岩.2000.一阶湍封闭的某些改进[J].青岛海洋大学学报,30(3):376-386.Liu F,Bi X Y.2000.Some improvement in first order closure scheme for turbulent diffusion[J].Journal of Ocean University of Qingdao,30(3):376-386.(in Chinese).

Qian M W,Longhetto A,Cassardo C,et al.2000.Heat energy balance in the convective atmospheric boundary layer at Xianghe(Beijing Area),China[J].J Atmos Sci,57(23):3881-3891.

Telford J W,Warner J.1964.Fluxes of heat and vapor in the lower atmosphere derived from aircraft observations[J].J Atmos Sci,21(5):539-548.

Wyngaard J C.1984.Toward convective boundary layer parameterization:A scalar transport module[J].J.Atmos Sci,41(12):1959-1969.

Wyngaard J C.1987.A physical mechanism for the asymmetry in top-down and bottom-up diffusion[J].J Atmos Sci,44(7):1083-1087.

Wyngaard J C,Weil J C.1991.Transport asymmetry in skewed turbulence[J].Physics of Fluids A:Fluid Dynamics,3(1):155-162.

张燕,徐玉貌.2002.三维非静力二阶闭合PBL模式的初步研究[J].南京气象学院学报,25(1):69-70.Zhang Y,Xu Y M.2002.Study on the 3-D nonhydrostatic 2nd-closure PBL model[J].J Nanjing Inst Meteor,25(1):69-70.(in Chinese).

周德刚,黄刚,马耀明.2012.中国西北干旱区戈壁下垫面夏季的热力输送[J].大气科学学报,35(5):541-549.Zhou D G,Huang G,Ma Y M.2012.Summer heat transfer over a Gobi underlying surface in the arid region of Northwest China[J].Trans Atmos Sci,35(5):541-549.(in Chinese).

K-theory is one of the most extensive turbulent closure revision schemes using weather patterns.However,because it cannot explain the counter-gradient transportation phenomenon,it must be corrected.There are three turbulent closure revision schemes representative of the convective boundary layer(CBL):the first was developed by Deardorff(1972),the second scheme by Holtslag and Moeng(1991),and the third by Liu Feng(2001).Because these schemes are based on different physical assumptions,they present different parameterizations and interpretations of counter-gradient transportation within the CBL.In the present work,using part of the published database obtained from the WL-ARPDD94 Experiment in Xianghe,the three schemes were tested and compared.The results showed that the first scheme systematically underestimates the heat flux within the entire CBL,and is inconsistent with the observations of the Xianghe CBL Experiment.The second scheme can reproduce inverse gradient transportation phenomena in most of the CBL,and can basically depict the vertical distribution of turbulent flux.However,it is not in agreement with observations in the lower and upper CBL.The third scheme’s counter-gradient item is related to height,reaching a maximum in the central CBL,while the other two schemes’ counter-gradient items remain constant with changes in height.The third scheme’s results are not only consistent with the second scheme in most of the CBL,but can also reasonably describe the turbulent flux distribution within the entire CBL.Liu’s parameterization exhibits good agreement with observations in the whole CBL.The analysis suggests that Liu’s scheme,first used to determine heat flux based on field experiment data,is able to represent the heat flux profile for the CBL.On the basis of reviewing the physical interpretation of counter-gradient transport phenomena by the different closure schemes,a universal scheme for the planetary boundary layer,suitable for numerical weather forecasting models,is urgently needed.

convective boundary layer;turbulent flux;parameterization;counter-gradient;transportation

(责任编辑：孙宁)

A case study of turbulent flux and counter gradient transport in the convective boundary layer

HAN Yongxiang1,2,SONG Haodong1,2,LIU Feng1,2,ZHAO Tianliang1,2

1CollaborativeInnovationCenteronForecastandEvaluationofMeteorologicalDisasters(CIC-FEMD),NanjingUniversityofInformationScience&Technology,Nanjing210044,China;2KeyLaboratoryforAerosol-Cloud-PrecipitationofChinaMeteorologicalAdministration,NanjingUniversityofInformationScience&Technology,Nanjing210044,China

doi：10.13878/j.cnki.dqkxxb.20130510001

引用格式:韩永翔,宋昊冬,刘烽,等.2016.对流边界层湍流通量及逆梯度输送参数化分析[J].大气科学学报,39(3):417-425.

HanYX,SongHD,LiuF,etal.2016.Acasestudyofturbulentfluxandcountergradienttransportintheconvectiveboundarylayer[J].TransAtmosSci,39(3):417-425.doi:10.13878/j.cnki.dqkxxb.20130510001.(inChinese).

*联系人，E-mail:shdly5330978@163.com