基于Nussbaum增益方法的UUV路径跟踪控制

齐　雪，才治军(.安徽科技学院　信息与网络工程学院，安徽　凤阳　3300;.安徽科技学院　财经学院，安徽　凤阳　3300)



基于Nussbaum增益方法的UUV路径跟踪控制

齐雪1，才治军2
(1.安徽科技学院信息与网络工程学院，安徽凤阳233100;2.安徽科技学院财经学院，安徽凤阳233100)

摘要:研究有界控制输入下欠驱动水下机器人(UUV)路径跟踪问题。UUV的水下运动通常靠推进器来实现，推进器所产生的推力大小受推进器形状、电力、水流情况以及UUV外形所决定，并且推力大小有一定的变化范围，这就要求对UUV进行控制器设计时要考虑控制的有界性这一限制。本实验以UUV路径跟踪为控制目标，引入一个辅助系统和Nussbaum增益函数来解决控制输入有界约束问题，其中辅助系统用来实现有界输入控制设计问题，Nussbaum增益用来估计控制器未知参数。通过Lyapunov稳定理论和仿真分析表明，所设计的控制器在保证闭环系统稳定的同时能使系统的控制输入增益始终保持在实际约束的范围内。

关键词:欠驱动水下机器人;路径跟踪;有界控制; Nussbaum增益

欠驱动水下机器人(UUV)动力学系统中各自由度相互耦合，水动力系数受UUV自身运动和外界环境的影响而发生变化，所以UUV动态系统是一个复杂的非线性控制系统，对于此系统控制问题的研究具有重要的理论意义和实际应用价值。研究UUV在二维水平面内的路径跟踪控制问题，不仅要求UUV路径跟踪精度达到要求的范围，还要求UUV的运动时间符合任务的时间规划需要［1］。这就需要同时考虑路径跟踪误差系统和速度跟踪误差系统稳定性的问题。

针对自治水下机器人采用Back stepping技术设计路径跟踪控制器［2］。此控制方法在保证路径跟踪精度的同时也能满足时间上的要求，而且控制器不存在奇异问题，便于理论和工程上的应用。通过采用滑模变结构控制方法进行自治水下机器人路径跟踪控制器设计，所设计的控制器对于系统模型参数不确定性和海流干扰有很强的鲁棒性［3－5］。通过将动态补偿器、神经网络与鲁棒控制相结合，提高了AUV在不确定环境中的路径跟踪能力［6－7］。通过采用虚拟向导牵引的方法，基于Lyapunov稳定理论和后推法设计自适应状态反馈控制器，实现AUV路径跟踪控制［8－9］。通过针对欠驱动水下机器人三维空间路径跟踪控制问题采用反步法设计动力学控制器，通过合理的选择控制器参数消除了部分非线性项，简化了虚拟控制量的形式，避免了采用传统反步法设计控制器时存在的奇异值问题［10］。

上述研究成果很少考虑控制输入约束的问题，而实际上UUV的水下运动通常靠推进器来实现，推进器所产生的推力大小受推进器形状、电力、水流情况以及UUV外形所决定，并且推力大小有一定的变化范围。所以UUV的纵向控制力和艏摇控制力矩不能无限增大，它们的变化是严格限制在某一区间上的，即输入量幅值约束。为了解决上述问题，基于Nussbaum增益方法设计了光滑有界的控制输入。通过引入一个辅助系统和Nussbaum增益函数，将系统增加一维，解决系统输入量幅值约束问题。另外，基于文献［11－12］，采用虚拟向导技术在Serret－Frenet坐标系下建立误差动态系统。基于视线角导航原理，设计虚拟控制量使UUV快速运动到目标路径上。同时结合Back stepping控制技术设计有界控制输入，从而实现闭环系统所有误差信号最终有界。

1　问题描述

欠驱动水下机器人(UUV)在水平方向的运动控制，分别存在纵向作用力和艏摇方向控制力矩。

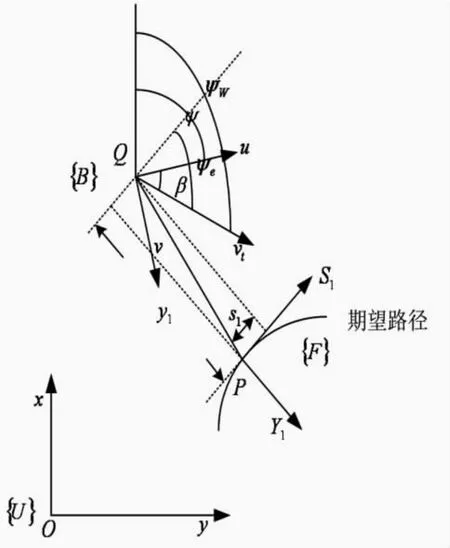
图1　路径跟踪示意图Fig.1 Path following reference frame for UUV

图1为UUV二维水平面路径跟踪示意图。{ U}、{ F}和{ B}分别代表惯性坐标系、Serret－Frenet坐标系和载体坐标系。P为期望路径上任意一点，以P点的切线方向S1和垂线方向Y1为坐标轴建立{ F}坐标系。Q为UUV的重心，与体坐标系原点OB重合。［x，y，ψ］T表示Q在惯性坐标系{ U}中的位置和姿态向量。ψ为艏摇角，用来确定从{ B}到{ U}的转换矩阵。［u，v，r］T为重心Q在{ B}中的线速度和角速度 向量，并且假设u≠0为合速度，当UUV横荡速度v≠0时，在载体坐标系下，径向方向u与合速度方向vt不一致，所以存在侧漂角s1，y1分别表示P点与Q点间距离在PS1轴，PY1轴上的投影长度。ψw为合速度vt与x轴之间的夹角，且为合速度vt与PS1轴之间的夹角。

UUV二维水平运动方程为:

将UUV载体坐标系{ B}绕ZB轴旋转角度β得到新的坐标系{ W}，在{ W}坐标系下，UUV水平运动学方程可以表示为:

合理忽略垂荡、纵摇和横摇运动后可以将UUV水平面运动和垂直面运动解耦［13］，此时，UUV水平动力学方程为:

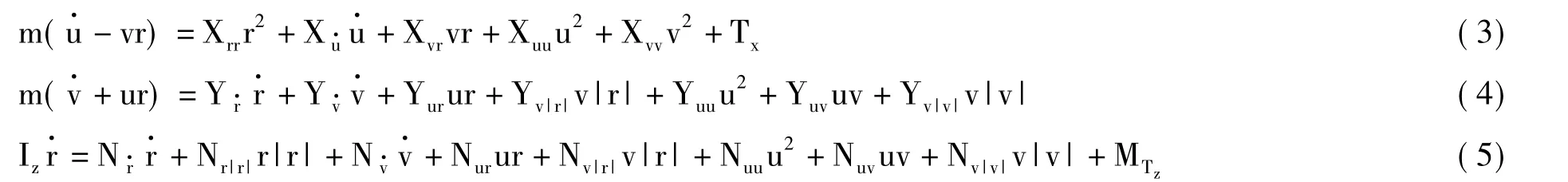
其中，m为UUV质量，X(·)，Y(·)和N(·)分别代表水动力系数，Iz为转动惯量，Tx为控制力，MTz为控制力矩。

公式(3)－(5)结构复杂，通过引入新的符号可以将其结构简化为以下形式:

式中，

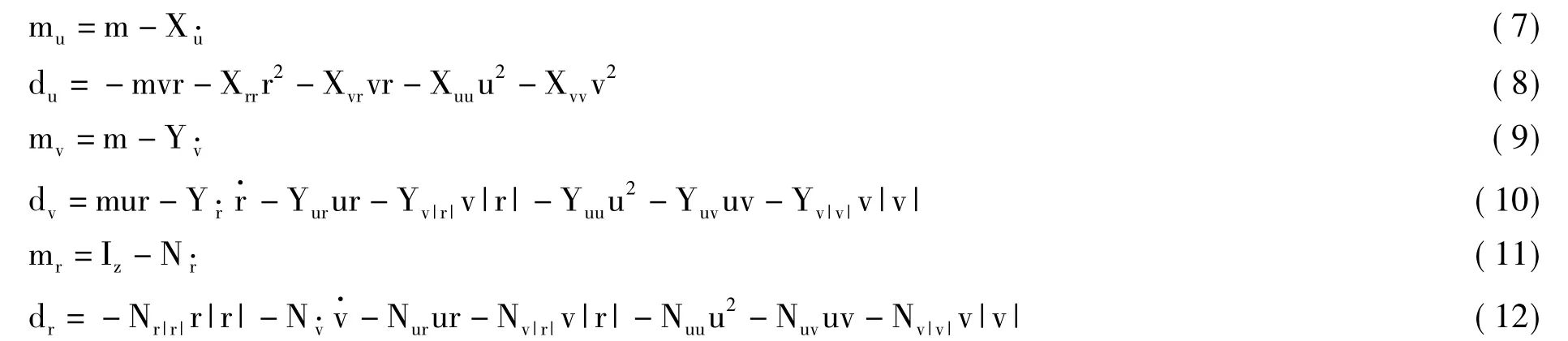
由于控制量Tx和MTz有界，即|Tx|＜TM，|MTz|＜MzM，TM＞0，MzM＞0.因此选择如下的光滑函数作为控制量:

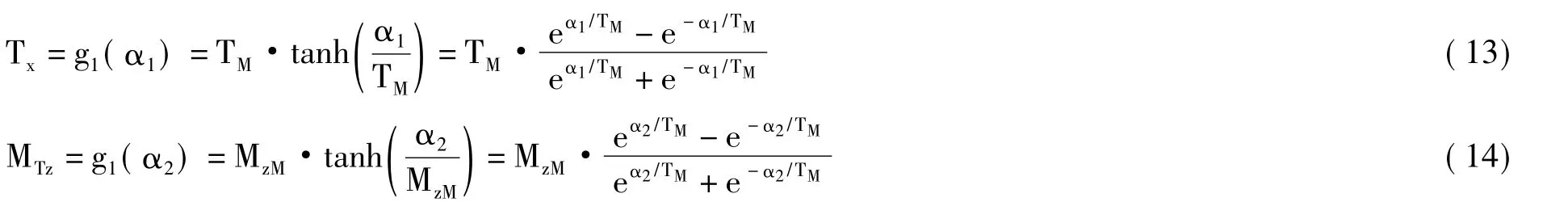
其中α1和α2是可设计的变量，其结构形式将在后文给出。

后文推导将用到如下假设:

假设1: gi(·)是紧集Ω上的光滑有界函数，即存在使得即函数gi(·)是严格为正或者为负的，在这里我们认为

假设2:存在正数gid＞0使得

下面给出控制器设计过程中将使用的定义和引理:

定义1:如果函数N(x)满足如下条件，则称N(x)为Nussbaum函数:

Nussbaum函数具有无限增益和无限转换频率的特点［14］。具有此类性质的函数如等.本文选用如下Nussbaum函数:

引理1:令V(·)和χ(·)都是［0，tf)上的光滑函数，并且为Nussbaum函数。若满足以下不等式:

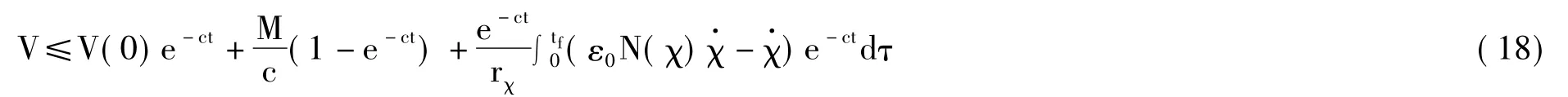
其中c＞0，rχ＞0，ε0＞0，M为正常数，则V(·)和χ(·)在［0，tf)上一定有界。

2　UUV路径跟踪控制器设计

为了保证UUV在路径跟踪过程中同时满足空间和时间的要求，结合图1，UUV路径跟踪控制器必须实现以下两个目标:

(I) UUV迅速运动到期望目标点，即控制实现UUV质心Q与期望路径上任意目标点P的距离为零，即，s1=0，y1=0 ;

(II) UUV沿着目标路径运动，即控制实现UUV合速度vt与PS1轴的夹角为零，即ψe=0.

基于上述讨论，需要建立相应的误差动力学系统，下面给出UUV在坐标系{ F}中的运动学模型:

其中cc(s)为期望路径的曲率，s为期望路径的参数变量。结合控制目标和模型(19)，对于给定的目标路径和期望纵向速度ud＞umin＞0，需要设计虚拟控制律r和，使得y1，s1，ψe渐进趋于零。为了实现上述控制目标，选择如下形式的视线角:

其中k0＞0，ε＞0均为视线角参数，为了保证视线角的存在，需要满足不等式k20－4ε≤0.

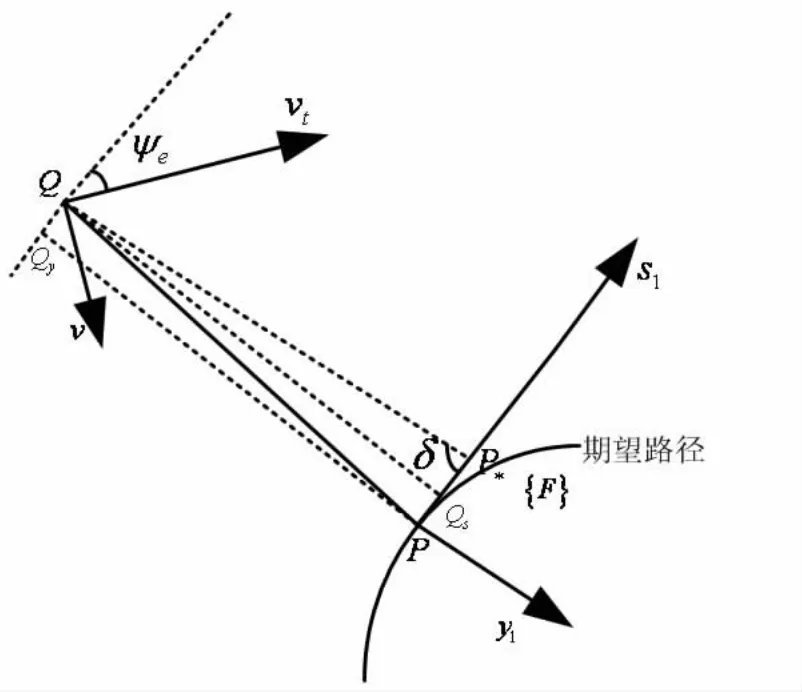
图2　曲线路径跟踪的视线角Fig.2　 Line of sight of curve path following

UUV路径跟踪控制器为(13)和(14)，其中，

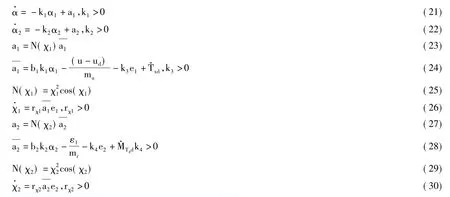
期望控制输入Txd和MTzd设计如下:

令控制输入误差为:

下面给出UUV路径跟踪控制问题的结论:

定理1:考虑UUV运动学模型(1)和动力学模型(6)，相应的跟踪路径误差模型(19)，利用视线角导航(20)，期望速度ud＞umin＞0.采用动力学控制律(13)，(14)，(21)－(32)，可使闭环系统所有误差信号最终有界。

证明:第一步:选择Lyapunov函数如下:

则Lyapunov函数的导数计算如下:

基于式(22)设计控制律为:

其中，k7＞0为控制器增益.则在此控制律作用下，Lyapunov函数的导数有如下结果:

第二步:选择新的Lyapunov函数如下:

则

其中，k8＞0为控制增益.使得

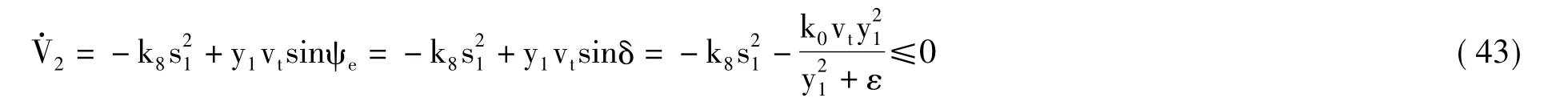
因此，(s1，y1) = (0，0)为系统平衡点。

第三步:对于r，定义虚拟控制律为

令ε1= r－r1为r的真实值和期望值之差，则

考虑总的Lyapunov函数为:

则

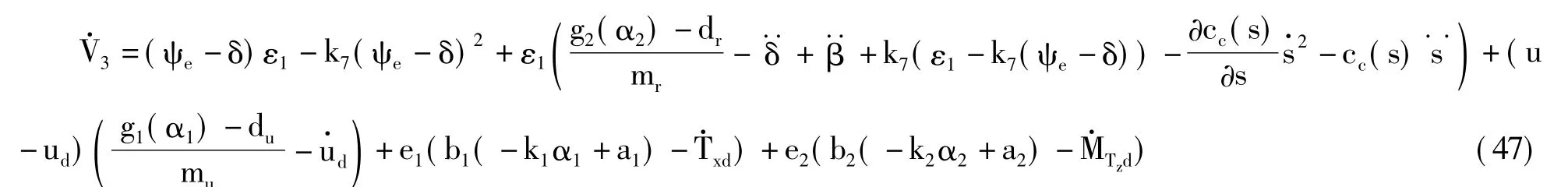
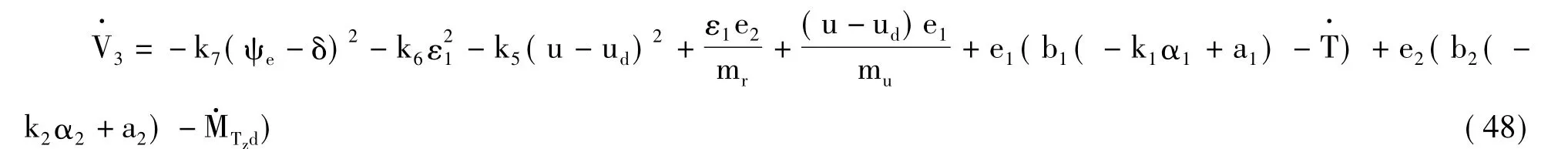
因为bi是随αi变化的，i =1，2.因此选取Nussbaum函数N(χi)替代bi.将控制项(21)－(30)带入(48)，得出如下不等式:

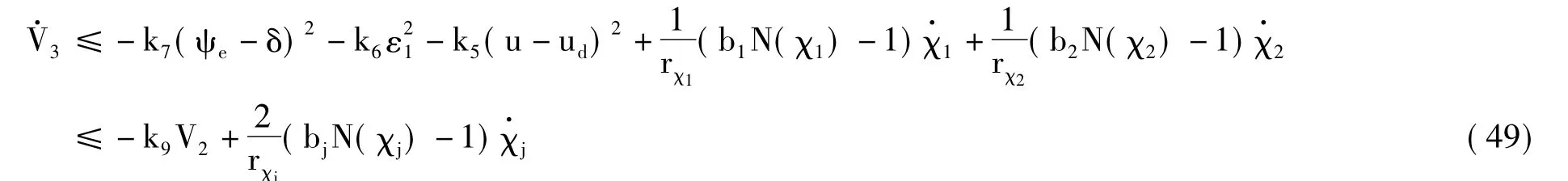
令不等式(49)在时间［0，t)上积分得:

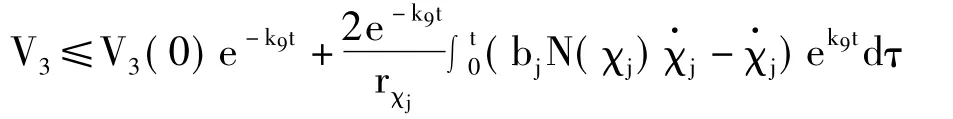
系统满足假设1－2和引理1，所设计的约束控制器能够保证闭环误差系统状态收敛，即闭环系统所有误差信号最终有界。

3　仿真分析

为了证明设计的控制器的有效性，本节基于INFANTE UUV进行了一些相关的数值仿真.所有仿真均基于MATLAB软件平台。下面给出INFANTE UUV动态系统相关参数:

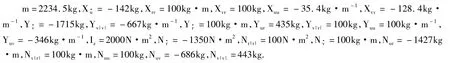
控制器参数选择如下:

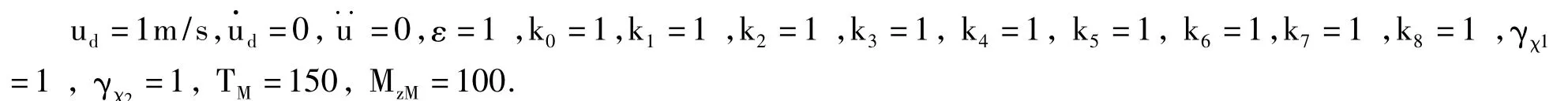
目标路径方程为:

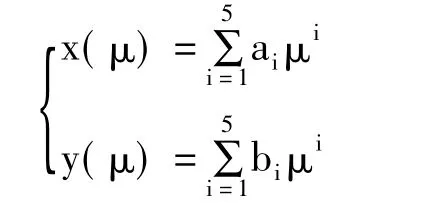
式中，

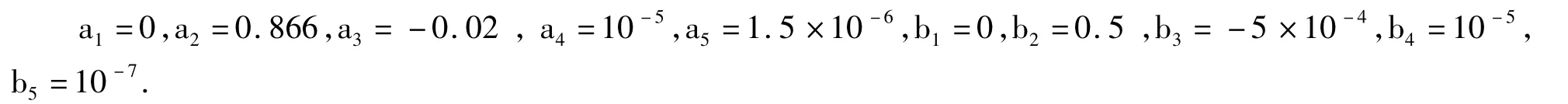
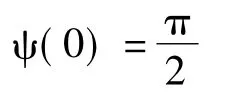
图3为UUV路径跟踪示意图，其中虚线为目标路径，实线为UUV实际运动路径。从图3可以看出: UUV能够在控制力和力矩的作用下运动到目标路径点上，并能沿目标路径运动。图4为UUV跟踪误差［s1，y1，ψe］T示意图。图5为UUV速度［u，v，r］T曲线图。由于S形曲线路径最后趋于直线，因此横荡速度v和首摇角速度r均趋于零，纵荡速度u趋于期望值ud=1m/s。图6为UUV控制输入［Tx，MTz］曲线图。

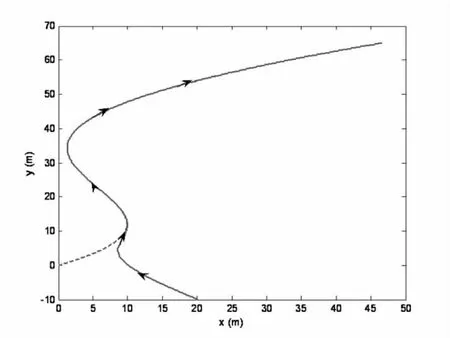
图3　UUV曲线路径跟踪图Fig.3 Curve path following for UUV

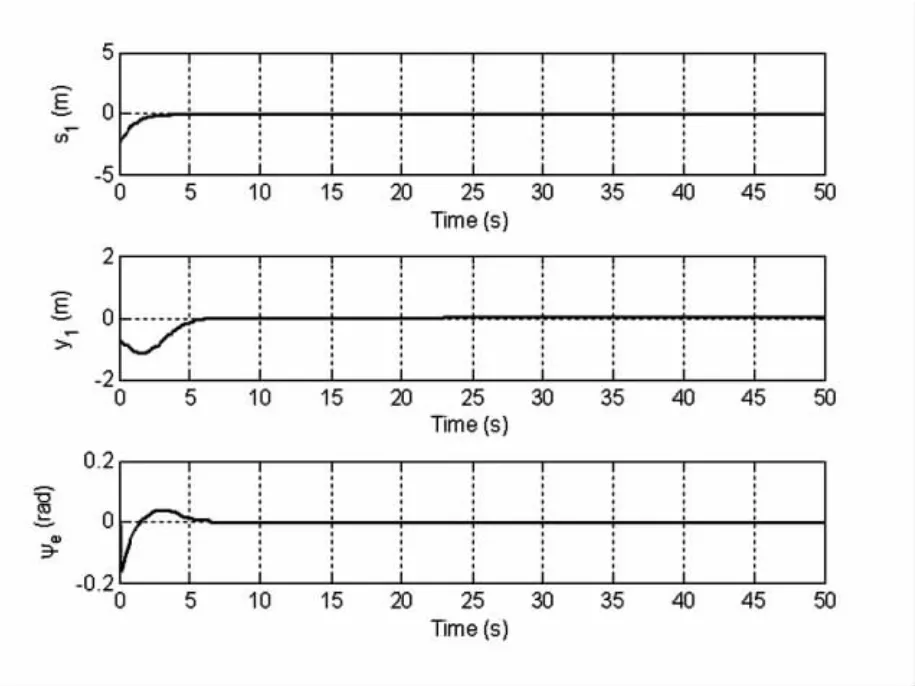
图4　UUV曲线路径跟踪误差Fig.4 Curve path following errors for UUV

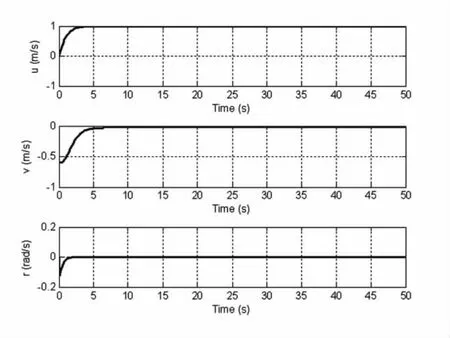
图5　UUV曲线路径跟踪速度Fig.5　 Curve path following velocities for UUV

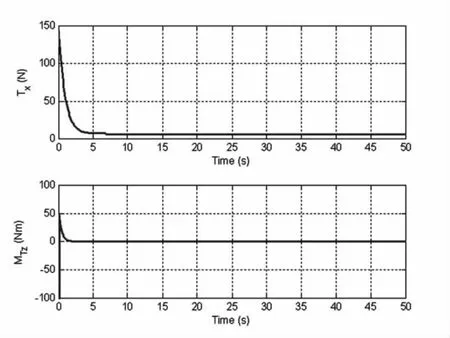
图6　UUV曲线路径跟踪控制输入Fig.6 Curve path following controllers for UUV

4　结论

本实验研究了有界输入限制下的UUV路径跟踪控制问题，给出了控制律光滑有界的设计方法，该方法的主要特点为:考虑了控制输入有界的限制，选择光滑有界函数设计控制器;对于控制器中的时变参数，选择Nussbaum函数对其进行补偿，使得控制输入具备适定性;同时考虑了UUV路径跟踪在空间和时间上的要求，使得所设计的控制器同时满足控制精度和时间约束的限制。

参考文献:

［1］向先波.二阶非完整性水下机器人的路径跟踪与协调控制研究［D］.武汉:华中科技大学，2010.

［2］LAPIERRE L，SOETANTO D.Nonlinear path－following control of an AUV［J］.Ocean Engineering，2007，34(11/12) : 1734－1744.

［3］马岭，崔维成.基于模糊混合控制的自治水下机器人路径跟踪控制［J］.控制理论与应用，2006，23(3) : 341－346.

［4］贾鹤鸣，程相勤，张利军，等.基于离散滑模预测的欠驱动AUV三维航迹跟踪控制［J］.控制与决策，2011，26(10) : 1452 －1458.

［5］边信黔，程相勤，贾鹤鸣，等.基于迭代滑模增量反馈的欠驱动AUV地形跟踪控制［J］.控制与决策，2011，26(2) : 289－292，296.

［6］Park B S，Yoo S J，Park J B，et al.Adaptive output－feedback control for trajectory tracking of electrically driven non－holonomic mobile robots［J］.Iet Control Theory＆Applications，2011，5(6) : 830－838.

［7］ZHANG Li－jun，QI Xu－e，PANG Yong－jie.Adaptive output feedback control based on DRFNN for AUV［J］.Ocean Engineering，2009，36(9/10) : 716－722.

［8］QI Xue.Adaptive coordinated tracking control of multiple autonomous underwater vehicles［J］.Ocean Engineering，2014，91 (S0029/8018) : 84－90.

［9］QI Xue，ZHANG Li－jun，ZHAO Jie－mei.Adaptive path following and coordinated control of autonomous underwater vehicles ［C］/ /2014 33RD CHINESE CONTROL CONFERENCE (CCC)，7，2014: 2127－2132.

［10］王宏健，陈子印，贾鹤鸣，等.基于反馈增益反步法欠驱动无人水下航行器三维路径跟踪控制［J］.控制理论与应用，2014，31(1) : 66－77.

［11］齐雪.自主水下机器人操纵运动的非线性控制方法研究［D］.哈尔滨:哈尔滨工程大学，2012.

［12］Peri A，Danza G，Benvenuti S，et al.New insights on the neuroprotective role of sterols and sex steroids: The seladin－1/ DHCR24 paradigm［J］.Frontiers in Neuroendocrinology，2009，30(2) : 119－29.

［13］蒋新松，封锡盛，王棣棠.水下机器人［M］.沈阳:辽宁科学技术出版社，2002.

［14］李利占.输入有界的TCSC自适应Backstepping控制设计［D］.锦州:辽宁工业大学，2014.

(责任编辑:马世堂)

Path following Control Based on Nussbaum Gain Method for Underactuated Underwater Vehicle

QI Xue1，CAI Zhi－jun2
(1.College of Information and Network Engineering，Anhui Science and Technology University，Fengyang 233100，China;
2.College of Finance and Economics，Anhui Science and Technology University，Fengyang 233100，China)

Abstract:Path following control problem of underactuated underwater vehicle (UUV) with bounded control input is studied in this paper.The underwater movement of UUV is usually achieved by the propeller.The thrust generated by the propeller is determined by the shape，power，water flow and UUV shape，and there is a certain extent of the thrust force，which is required to be considered in the UUV controller designing process.In this paper，based on the UUV path following control target，an auxiliary system and Nussbaum gain functions are proposed to overcome the problem of input constraint.Based on Lyapunov stability theorem and simulation analysis，the designed controller can keep the closed－loop system stable and make the system control input gain always stay within the scope of the actual constraints as well.

Key words:Underactuated underwater vehicle; Path following; Bounded control; Nussbaum gain

中图分类号:TP242.6

文献标识码:A

文章编号:1673－8772(2016) 02－0051－08

收稿日期:2015－11－16

基金项目:安徽高校自然科学研究重点项目(KJ2016A174，KJ2015A242)。

作者简介:齐雪(1981－)，女，黑龙江省牡丹江市人，博士，讲师，主要从事非线性系统控制理论与应用研究。