双轴汽车制动力分配因数的优化设计

卫文涛，高　峰

(北京航空航天大学 交通科学与工程学院,北京 100191)



双轴汽车制动力分配因数的优化设计

卫文涛，高峰

(北京航空航天大学 交通科学与工程学院,北京 100191)

摘要：根据制动时整车的受力模型，确定了整车同步附着因数、利用附着因数和制动效率的计算方法。将制动力分配因数作为优化变量，满载与空载的使用频率、实际利用附着因数作为考虑因素，提出了一种使整车具有良好制动性的优化方法，得到的优化结果既符合联合国欧洲经济委员会(ECE)制动法规的要求，又能保证制动效率不小于70%。本文以某轻型货车作为分析实例并进行了优化设计，优化结果显示：在法规要求的速度条件下，制动距离有明显的减小。

关键词：ECE法规；制动力；分配因数；优化设计

0引言

在车辆制动系统的设计过程中，首先要考虑的就是制动性能。制动系统必须尽可能快地使汽车减速或停止，并且维持汽车在路面上行驶时方向的稳定和可操控[1-4]。前后制动力分配是汽车制动性能很重要的影响因素。文献[5-6]根据联合国欧洲经济委员会(ECE)制动法规求出了前后轴制动力分配比的取值范围，但结果仅仅满足了制动法规的要求，并未实现制动性能的最优。文献[7-9]虽然提出了一种考虑满载和空载使用频率的情况下，满足整车具有良好制动性能的优化方法，但没有考虑到同步附着因数对于前后轴车轮利用附着因数的影响。实现制动力的合理分配，既要考虑不同载荷的使用频率，也要考虑同步附着因数对汽车实际使用附着因数的影响。在充分考虑以上两种影响因素的情况下，本文提出了一种能够使整车具有良好制动性能的前后制动力分配方法。

1模型的建立

图1　制动时汽车受力图

理想制动器制动力分配曲线与实际制动器制动力分配曲线交点处的附着因数称为同步附着因数，用φ0表示，可得：

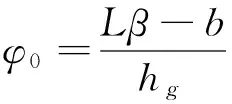
(1)

其中：β为制动力分配因数。

用φi表示汽车的利用附着因数，z表示地面附着因数，则前后轴的利用附着因数分别为：

(2)

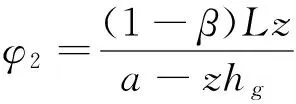
(3)

制动效率通常也用来描述地面附着因数的利用程度，其值可用来说明制动力分配的合理性。前轴的制动效率为：

(4)

后轴的制动效率为：

(5)

2制动力分配的优化设计

2.1优化变量的选取

对汽车进行制动时，汽车产生总的制动力，通过前后制动力分配因数β在前后轴之间进行分配。制动力分配因数对前后轴制动力的取值以及制动效率有决定性的影响，因此在优化过程中将β作为变量。

2.2目标函数的确定

汽车以一定的减速度进行制动时，不发生车轮抱死所要求的最小路面附着因数总大于其制动强度(制动强度与地面附着因数相等时除外)。附着因数与制动强度越接近，地面的附着性能发挥得越充分，则汽车的制动力分配合理程度越高[10]。因此，在制动强度范围内(z=0.15～0.80)，汽车的利用附着因数在尽可能接近车轮刚要抱死需要的利用附着因数时，地面的附着条件发挥得越充分，汽车轴间制动力分配越合理。

在实际设计过程中，考虑到汽车在不同载荷工况下的使用概率存在差异，分别为满载与空载工况赋予相应的权值，从而实现对不同工况的综合考虑。在目标函数的实际中，满载工况的权值设定为w，那么相应的空载工况的权值为(1-w)。

设汽车行驶时的同步附着因数为φ0，则进行制动的路面上φ<φ0时，前轮提前抱死，则在这个范围内后轴的利用附着因数φ2曲线无意义。因此在φ<φ0时，汽车的利用附着因数曲线应取φ1所确定的曲线。在φ>φ0的路面上制动时，情况正好相反，即φ1曲线无意义。因此φ>φ0时，汽车的利用附着因数应取φ2所确定的曲线[12]。

综合考虑以上因素，以制动减速度因数z为被积函数的自变量，z的取值范围为被积函数的积分区间。当φ<φ0时，以汽车前轴实际利用附着因数曲线与理想线间差值的平方和为被积函数；当φ>φ0时，以汽车后轴实际利用附着因数曲线与理想线间差值的平方和为被积函数。以β为优化变量，分别考虑满载与空载，建立目标函数。通过对目标函数进一步分析，当目标函数取最小值时，所求得β为最优值。

只考虑满载时的目标函数为：

(6)

只考虑空载时的目标函数为：

(7)

考虑到实际的装载情况，最终确定的目标函数为：

F(β)=w×P1+(1-w)×P2。

(8)

式(6)～式(8)中：w为满载工况的权值；φ01和φ02分别为满载和空载时同步附着因数；φ11和φ21分别为满载时前、后轴车轮利用附着因数；φ12和φ22分别为空载时前、后轴车轮利用附着因数。

2.3约束条件

(Ⅰ)为了保证制动时汽车的方向稳定性和有足够的制动效率，ECE R13 制动法规[13]对双轴汽车前、后轮制动器制动力提出了明确的要求，因此将ECE制动法规作为约束条件。

(Ⅱ)整车的最小制动效率应满足Emin>70%[7]。

2.4对ECE制动法规的分析

ECE制动法规对各类两轴车辆的规定[13-14]如下：

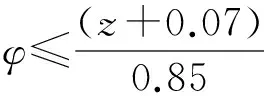
对除M1、N1类型以外车辆有如下规定：(Ⅰ)制动强度z=0.10～0.61，满足于附着因数φ≤(z+0.07)/0.85。(Ⅱ)当制动强度z=0.15～0.30，若各轴利用附着因数曲线位于由φ=z+0.08和φ=z-0.08确定的两条平行于理想利用附着因数曲线之间，则认为满足要求；当z≥0.03时，后轴利用附着因数要满足φ≤(z-0.02)/0.74。

经过化简并将满载和空载情况下的各参数代入以上各种情况，便可初步确定β的取值范围。

3优化模型的求解及结果

将某轻型货车作为研究对象，进行制动力分配的优化设计。表1为该车型相关的技术参数[7]。

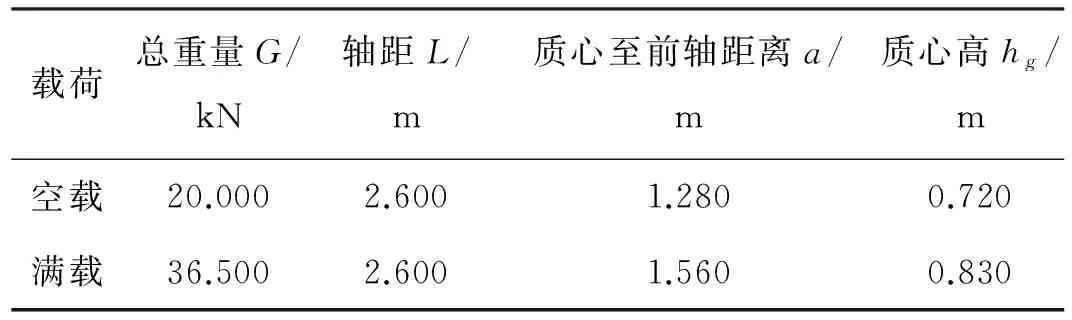
表1　某轻型货车相关技术参数

利用表1中的数据建立该车的数学模型，根据前面所叙述的方法对该轻型货车的制动力分配进行优化设计。本文采用的是美国PTC公司旗下的一款工程计算软件mathCAD，利用mathCAD环境中的求解与优化扩展库，求解在约束条件下的最优解问题。

由于该车属于N2类汽车，将相应约束条件代入可得：空载时汽车制动力分配因数的取值为0.576≤β≤0.700；满载时制动力分配因数的取值为0.469≤β≤0.628。因此，综合考虑两种工况，汽车制动力分配因数的约束条件为：0.576≤β≤0.628。

由于在这个制动力分配因数取值范围内，满载和空载的同步附着因数均位于区间[0.15，0.80]，从而可通过式(6)和式(7)确定P1、P2的取值，将P1与P2的值代入式(8)可得最终目标函数的形式为：

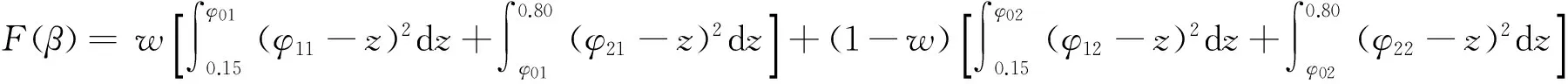
(9)

设定考虑满载的权重分别为0，0.2，…，1.0，对目标函数的变化趋势进行分析，将目标函数与制动力分配因数的关系绘制成曲线，如图2所示。

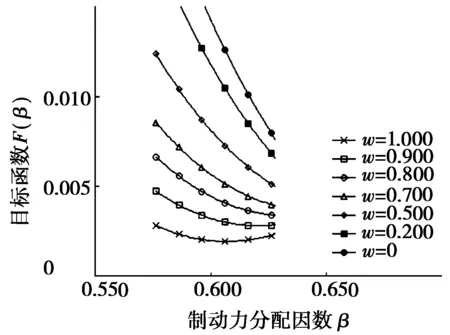
图2　目标函数随制动力分配因数变化曲线

图2中，在较小满载权重w的情况下，目标函数的曲线是单调递减的，因而有单一的最小值，目标函数取最小值时，自变量取上限值为优化结果，此时β=0.628。在较大满载权重的情况下，目标函数的变化趋势为一凹形曲线，因此有单一的最小值，在最小值时所对应的制动力分配因数是优化结果。经计算，当w≤0.848时，目标函数为一单调递减的曲线；当w>0.848时，目标函数为一凹形曲线。因而，使得目标函数达到最小值的优化变量取值如下：当w≤0.848时，使目标函数F(β)取得最小值，所对应的β为0.628；当w=0.900时，使目标函数F(β)取得最小值，所对应的β为0.621；当w=1.000时，使目标函数F(β)取得最小值，所对应的β为0.607。

4结果验证

4.1ECE制动法规验证

为了验证所得的结果是否符合ECE制动法规的要求，将ECE制动法规的曲线和满载与空载时整车利用附着因数曲线进行对比，其结果见图3～图5。经过对比发现：在w取不同值的情况下，满载与空载优化后的利用附着因数曲线均在ECE制动法规所要求的范围之内。

图3 w≤0.848时,优化后的利用附着因数曲线图4 w=0.900时,优化后的利用附着因数曲线

4.2制动效率验证

当w取不同值时，整车的制动效率随地面附着因数变化见表2～表4。由w取不同值时，所求得的前后轴制动力分配因数β也完全不一样。由优化后制动效率与地面附着因数的关系可知：w取不同值时，整车满载与空载状况时的制动效率均大于70%，达到了约束条件对制动效率的要求。

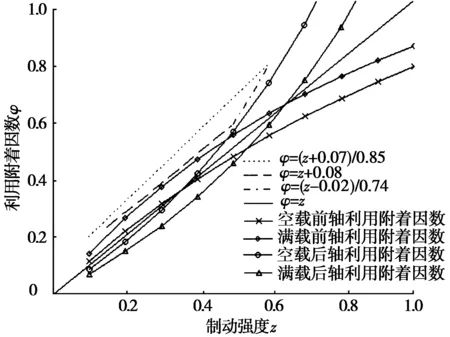
图5　w=1.000时，优化后的利用附着因数曲线

4.3制动距离验证

制动距离是制动效能的评价指标。根据制动效率与地面附着因数的关系来确定汽车所能达到的最大减速度，按照下式进行制动距离的计算[15]：

(10)

表2　w≤0.848时，各地面附着因数情况下整车制动效率

表3　w=0.900时，各地面附着因数情况下整车制动效率

表4　w=1.000时，各地面附着因数情况下整车制动效率

为了证明本文优化后的效果，与文献[7]中的优化后制动距离进行比较，对比结果如表5所示。

表5　优化后制动距离的对比

由表5可知：当w=0.500时，本文优化后制动距离较文献[7]提出的优化方法，满载时缩短了0.1 m，空载时缩短了0.3 m。当w=0.750时，本文优化后制动距离较文献[7]提出的优化方法，满载时缩短了0.1 m，空载时缩短了0.7 m。当w=1.000时，本文优化后制动距离较文献[7]提出的优化方法，满载时缩短了0.3 m，空载时缩短了0.2 m。

通过与文献[7]中优化方法所得的制动距离的对比，w取不同值时，在法规规定的路面上优化后，该轻型货车制动距离均小于文献[7]中优化后所得的制动距离。因此，该车在充分考虑满载与空载的情况下，优化设计制动效能与整车行驶安全性均能得到提高。

5结论

(1)提出了使各类双轴车辆制动效能达到最优值时，制动力分配因数β的求解方法。

(2)以某一车型为例进行计算，得到了优化设计的结果，验证了优化结果既满足ECE制动法规，也满足制动效率的要求。

(3)为了验证所得到的结果是否可以使整车具有更好的制动效能，将优化后的制动距离与文献[7]所提出方法的优化结果进行对比，表明本文优化方法具有更高的优化效果。

参考文献：

[1]胡爱军,王朝晖.汽车主动安全技术[J].机械设计与制造,2010(7):97-99.

[2]BUSCHMANN G,HANS T,KUHN W.Electronic brake force distribution control-a sophisticated addition to ABS[J].SAE paper,1992:920646.

[3]LIMPERT R.Brake design and safety[M].2nd ed.Warrendale:Society of Automotive Engineers,1999.

[4]KIMBROUGH S,ELWELL M.An advanced braking and stability controller for two vehicle and trailer combinations[J].SAE paper,1993:931878.

[5]张立军,朱博,贾云雷.依ECE法规进行汽车制动力分配新方法[J].辽宁工程技术大学学报,2005,24(2):276-279.

[6]杨啟梁.低速货车制动力分配因数研究[J].拖拉机与农用运输车,2006,33(2):65-67.

[7]王亚晴,张代胜,沈国清.汽车制动力分配比的优化设计与仿真计算[J].合肥工业大学报(自然科学版),2005,28(11):1393-1396.

[8]汪文国.农用运输车制动系优化设计与仿真计算[J].农业机械学报,1998,14(1):108-111.

[9]陈春生.商用车联合制动系统制动力分配因数的优化[J].机电技术,2013(2):115-118.

[10]余志生.汽车理论[M].北京:机械工业出版社,2001:89-129.

[11]LIAN Y F,TIAN Y T,HU L L,et al.A new braking force distribution strategy for electric vehicle based on regenerative braking strength continuity[J].Journal of central south university,2013,12(20):3481-3489.

[12]刘惟信.汽车制动系的结构分析与设计计算[M].北京:清华大学出版社,2004:44-48.

[13]欧洲经济委员会.有关M、N和O类车辆制动认证的统一规定[S/OL].2001.http://www.docin.com/p-986856722.html.

[14]方泳龙.汽车制动理论与设计[M].北京:国防工业出版社,2005:32-37.

[15]王宣锋,应国增,黄朝胜.某微型客车制动力分配优化设计[J].汽车技术,2009(9):1-5.

[16]中国国家标准化管理委员会.机动车运行安全技术条件:GB 7258—2004[S].北京:中国标准出版社,2012:19.

基金项目：国家自然科学基金项目(51275019)

作者简介：卫文涛(1991-),男,河南项城人,硕士生;高峰(1955-),男,河南洛阳人,教授,博士，博士生导师，主要从事智能车辆/特种车辆及车辆非常规行走机构等方面的研究.

收稿日期：2016-01-30

文章编号：1672-6871(2016)04-0020-06

DOI:10.15926/j.cnki.issn1672-6871.2016.04.005

中图分类号：U461.3

文献标志码：A