政府主导、固定资产投资对城镇化地区差异影响分析

■ 赵旭宏　博士生（北京大学经济学院　北京　100871）



政府主导、固定资产投资对城镇化地区差异影响分析

■ 赵旭宏博士生（北京大学经济学院北京100871）

内容摘要：本文通过建立VAR模型发现，城镇化水平差异和城镇固定资产投资差异具有长期协整关系，政府在不同地区的非均衡投资是城镇化区域差异的长期原因。基于VECM的Granger因果关系表明，城镇固定资产投资地区差距是城镇化地区差距的短期和长期Granger原因。长期内，城镇化地区差距将会影响城镇固定资产投资的地区差距。要实现区域间的均衡发展，政府必须调整区域发展政策，使各个地区逐步享受全国统一的国民待遇。

关键词：城镇化政府引导固定资产投资VAR模型

改革开放初期，我国政府实施东南沿海区域优先发展的政策。在政府引导下，我国出现了大规模的人口跨区域流动。刘玉（2008）利用第五次人口普查数据，分析发现中国人口流动具有显著的地域集中性和空间指向性，东部地区是主要人口流入地，中部地区是主要人口流出地。鲁奇、王国霞等（2006）利用“四普”、“五普”数据发现流动人口的地理分布向东部地区集中的趋势不断加强，而在环渤海地区有所下降，有进一步向长三角和珠三角及福建集中的趋势。农村人口向这些地区流动，直接提高了流入区的城镇化水平。

农村人口向沿海地区流动，与沿海地区经济高速增长有直接相关性。而我国作为投资驱动型国家，固定资产投资对经济增长的地区差异具有显著的影响。这样，地区固定资产投资差异导致经济增长水平的差异，从而引发人口跨地区流动，形成城镇化发展水平的区域差异。在我国现行体制下，各级政府拥有土地审批权，固定资产投资一般需要政府土地审批支持。因此，政府能够在很大程度上影响固定资产投资的规模。固定资产投资一般来源于国家财政直接投资、银行贷款、外商直接投资、民间资本等渠道。政府对这些渠道无论是通过财政转移支付、影响银行信贷资金投向、招商引资等政府行为均有较大的影响力。

为了通过固定资产投资地区间差异来分析政府政策效果。本文对作为人口输入区的京津沪、江苏、浙江、福建和广东等7个省份和其他作为人口输出区的省市，在1978-2011年间城镇化水平的差异与在固定资产投资差异变动的关系进行实证分析，来定量分析政府政策的作用。实证分析过程使用Eviews7.1完成。

模型构建

（一）构建模型

本文建立了向量自回归模型（VAR）和误差修正模型（VECM），并进行协整检验和格兰杰因果关系检验，利用脉冲响应函数来检验二者之间的动态关系。VAR模型由Sims（1980）年提出，是AR模型的一种推广，常用作分析相互关联的时间序列系统及随机扰动项的动态变化。VAR模型不以经济理论为基础，把系统中每一个内生变量作为所有内生变量的滞后值的函数来构造模型，从而避开了结构化建模的需要。一般的VAR（p）模型的表达式为：

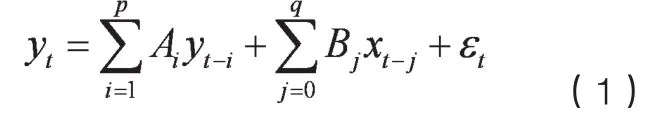
其中，yt是k维内生变量，xt是n维外生变量，At和Bj是待估计的参数矩阵，p是内生变量的滞后期，q是外生变量的滞后期。

（二）区域差异的测度

对区域经济差异的研究，目前已经有多种测度方法，包括基尼系数法、变异系数法和Theil指数法等。Theil指数法能够将总体的区域差异分解成不同空间尺度的内部差异和外部差异，刻画各个区域对总体差异的贡献和区域内部差异的变化情况。Theil指数T与基尼系数（Gini coefficient）具有相似和相同之处，本质上是一个研究对象的收入与群组收入平均水平对比的测度。但在分组情况下Theil指数可以将组内差异完美地分配到组间差异上。

如果以各地区城镇常住人口数量为“收入”，假设Uij为i区域j地区的城市人口数量，为i区域城市人口，Pij表示i区域j地区的城乡总人口数量，为地区总人口，U=∑Ui，P=∑Pi则根据Shorrocks（1980）的推论，有：

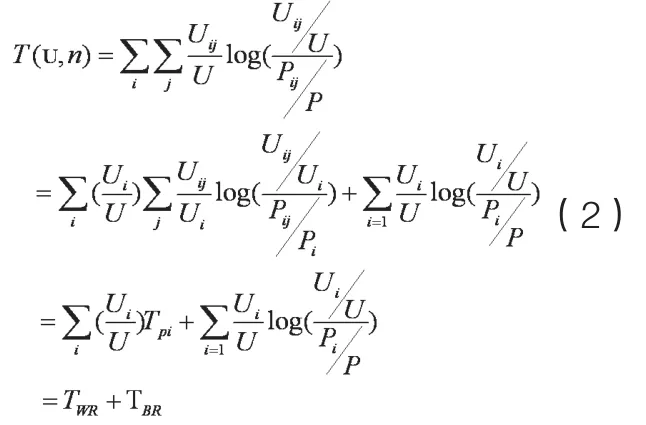
其中，Tpi为区域i内部的各省的城镇化水平差异。

可以看出，T可以分解为组内差异TWR和组间差异TBR，可以计算组内差距和组间差距对总差距的贡献。T（u，n）考虑了各地区不同的城乡总人口规模，其研究对象是一个地区的人口所能达到的“收入”—城镇常住人口数量。

固定资产投资的地区差异也可以使用同样的方法来测算，本文对输入区和输出区城镇化水平差距用THLt来表示，城镇固定资产投资的差异用IFAt来表示。各地区城镇固定资产投资数据取自《新中国60年统计资料汇编》、国家统计局网站国家数据库。

实证分析

（一）变量平稳性检验

为了避免建模过程中的“伪回归”现象，所研究的变量必须具有同阶平稳性并且具有协整关系。因此，首先检验THLt和IFAt是否存在单位根。对单位根的检验有DF检验、ADF检验、PP检验、ERS检验、NP检验等方式，后三种新兴方法克服了前者原序列可能含有常数项和趋势项的假设，但应用比较复杂。本文使用ADF检验法进行单位根检验。ADF检验法可以设定三种模式，分别包括趋势项和常数项、只包含常数项、两者都不包含。对于滞后期p值的选择，采用赤池信息准则（AIC）和施瓦茨信息准则（SC）来确定最优。通过单位根检验可知，在三种模式下，变量THLt和IFAt水平序列（原序列）均拒绝了零假设，为非平稳序列。而经过一阶差分后△THL和△IFA为平稳序列，即原序列均为一阶单整过程I（1）。单位根检验结果如表1所示。

（二）协整检验

由于变量THLt和IFAt均是一阶平稳序列，需要进行协整分析来判断二者之间是否存在协整关系。常用的协整检验方法有EG两步法和JJ （Johanse-Juselius）协整检验，由于JJ协整检验采用极大似然估计，可以给出全部协整关系且功效更稳定，因此本文使用这一检验方法。

进行JJ协整检验首先要建立VAR模型，此时需要选择合理的滞后区间。对于VAR模型滞后区间的选择一般采取LR（似然比）统计量、FPE（最终预测误差）、AIC信息准则、SC信息准则、HQ信息准则等。其中，LR统计量越大越好，其它4个统计量越小越好。如果5个信息准则给出的滞后期数不同，则选择通过3个标准以上的准则为准，且LR是最重要的参考标准。这样，VAR模型既可以尽可能完整地显示模型的动态过程，又不至于因为待估计的参数过多而使模型自由度太小，影响参数估计的有效性（高铁梅，2009）。

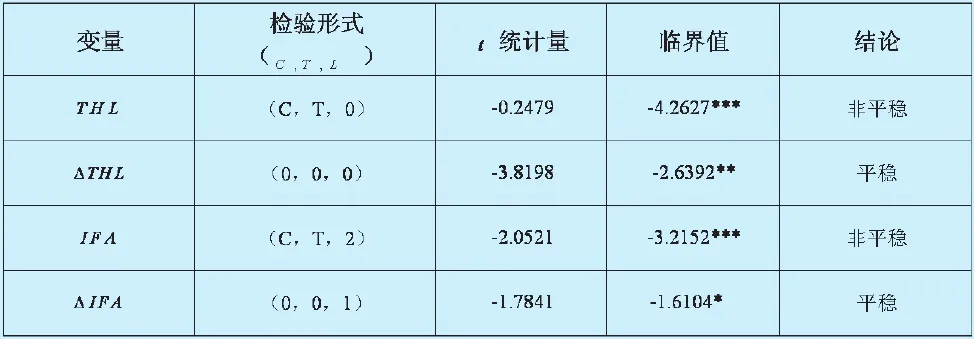
表1　ADF单位根检验结果

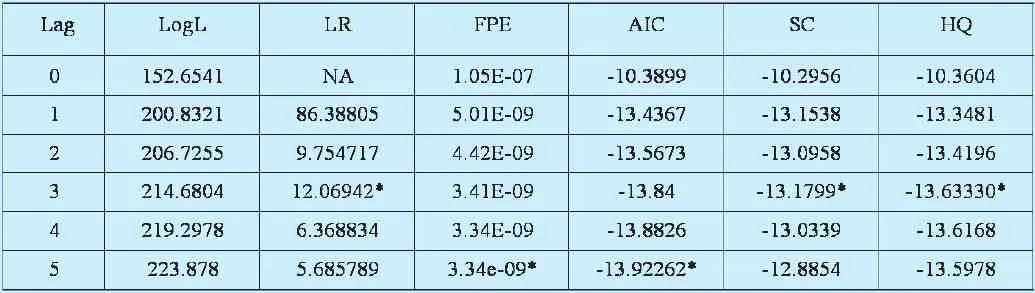
表2　VAR模型最优滞后期的选择

表3　JJ协整检验迹检验结果

表4　JJ协整检验最大特征根检验结果

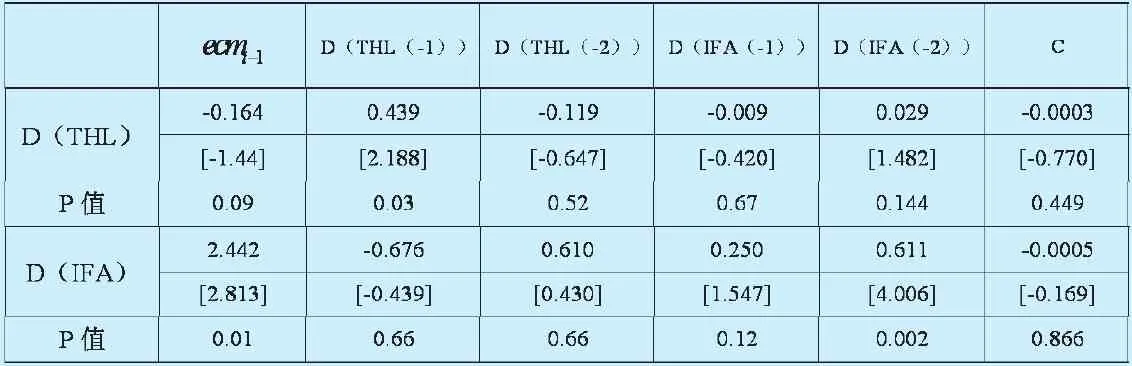
表5　VECM的估计结果

表6　短期Granger因果关系检验1

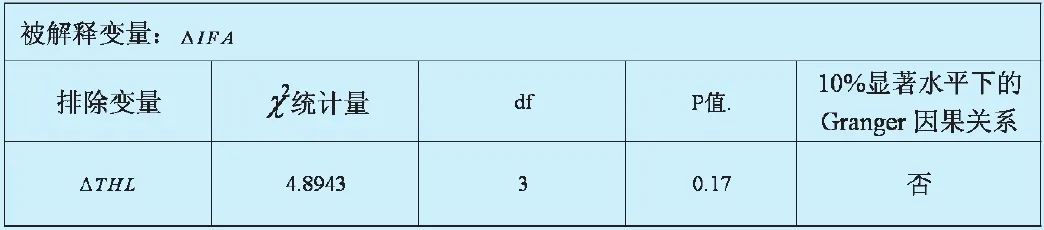
表7　短期Granger因果关系检验2

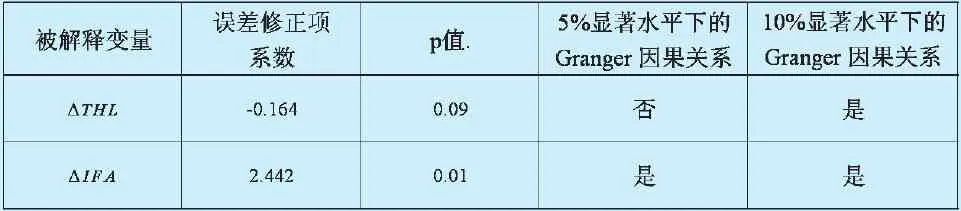
表8　基于VECM的长期Granger因果关系检验

由表2可知，LR、SC和HQ 三种方法选择的最优滞后期数均为4期，按照少数服从多数的原则，本文选取滞后3期阶数，建立VAR（3）模型：

根据Johansen（1995），协整方程同原时间序列一样，也可能有截距和确定的趋势。由于本文建立的VAR（2）允许有确定性趋势，协整方程只有截距项，因此采取结构（3）进行检验。内生变量的一阶差分滞后阶数按照P-1选取滞后阶数2。JJ协整检验迹检验结果如表3所示。

根据迹检验的结果，由于迹统计量16.83大于5%显著水平下的临界值15.49，即在95%的置信水平上拒绝了原假设，说明存在协整方程。为了进一步验证协整关系是否存在，进行最大特征根检验。JJ协整检验最大特征根检验结果如表4所示。

迹统计量和最大特征根检验结果表明，在95%的置信水平上，可以接受存在一个协整关系的假设，固定资产投资和城镇化的地区差异之间存在长期的协整关系。标准化的协整方程如下：

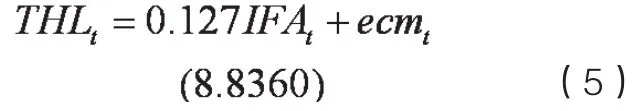
上式中，ecmt表示城镇化和固定资产投资地区差异线性组合的残差，括号里表示t值。通过协整方程可以看出，城镇化和固定资产投资差距存在稳定的正向协整关系，当固定资产投资的地区差距每扩大1个单位，城镇化地区差异相应上升0.127个单位。而当固定资产投资的地区差距下降时，城镇化地区差距也相应下降，与常理比较符合。

在确定了变量之间的协整关系之后，可以通过AR根验证协整关系的稳定性。AR特征方程的特征根的倒数绝对值如果小于1，即位于单位圆内，则模型是稳定的，否则就是不稳定的。本文共有p×k=4个AR特征根，观察AR根分布图，可以看出所有特征根均在单位圆内，协整模型是稳定的。

（三）向量误差修正模型

由协整检验可知，变量THLt和IFAt存在长期均衡关系，但实际经济数据却是由“非均衡过程”生成的，不仅有长期趋势，还有短期波动的影响。为此，Enger 和Granger（1981）将协整和单方程误差修正模型（ECM）结合起来，建立起了向量误差修正模型（VECM）。这可以看作是含有协整约束的向量自回归VAR模型。对于一般的VAR（p）模型，有：

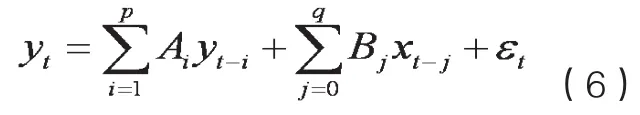
经过差分变换后有：

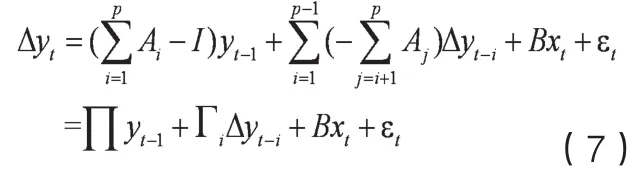
假设∏矩阵的秩为r且0＜r＜k，则矩阵可以分解成两个k×r阶、秩为r的矩阵α和β的乘积：

代入上式可得：

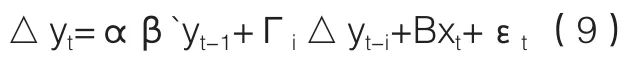
其中，β`为协整向量矩阵，β`yt-1是误差修正项，反映变量之间的长期均衡关系，用ecmt-1表示；调整系数向量α反映变量之间均衡关系偏离长期均衡状态时调回到均衡状态时的速度。Γi反映各变量短期波动的冲击。在进行协整检验的基础上，误差修正模型VECM表示为：

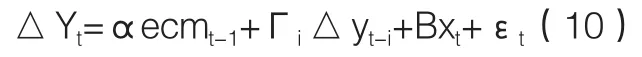
根据这一思路，在VECM中协整关系可以表达成为误差修正项的形式：

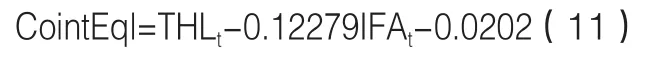
误差修正项的表达式与JJ协整检验中得到的协整关系的系数是一致的。进行估计时VECM模型中两个方程的解释变量不再是原序列，而是原序列的差分序列（用D表示）。△THLt和△IFAt方程均满足负向修正机制，系数如表5所示。

从△THLt方程可以看出，误差修正项ecmt-1在10%的显著水平上对城镇化的地区差距的短期变动具有负向影响。当城镇化和城镇固定资产投资地区差距偏离长期均衡时，长期修正关系将以0.164的力度拉回均衡状态，即在IFA不变的情况下，THL 在t期的变化（D（THL）=THL-THL（-1）将会消除前一期16.4%的非均衡误差。从变量自身的短期波动看，滞后一期城镇化区域间差异自身的波动对当期城镇化的区域间差距在5%的显著性水平上有显著的影响，其他变量则不显著。方程的R2值为0.32，AIC=-8.98，SC=-8.70，取值比较理想。△IFAt方程不满足负向修正机制，在此不做分析。通常我们更关心VECM整体的检验结果，AIC=-13.94，SC=-13.29，都比较小，说明VECM模型比较合理。

（四）短期和长期因果关系检验

由VAR模型协整检验可知，THLt和IFAt存在长期协整关系。本文长期因果关系检验应基于VECM进行，它可以从短期和长期两个方面来分析变量之间的动态影响。短期Granger因果关系检验可以分析短期影响，即解释变量从1到p-1 阶滞后值系数的联合分布显著性。如果联合分布的零约束检验被拒绝，则说明滞后项变量对被解释变量存在Granger因果关系。

从表6结果可以看出，在△THLt方程中在10%的显著水平下能够拒绝城镇固定资产投资差距不是城镇化地区差距的Granger原因的原假设，表明城镇固定资产投资内生于系统，在Granger意义下短期内影响城镇化地区差距。这与改革开放后我国经济作为投资驱动型经济模式，固定资产投资对工业化和城镇化具有实质性影响的实际相吻合。

从表7的结果可以看出，在△IFA方程中在10%的显著水平下不能拒绝城镇化地区差距不是固定资产投资差距的Granger原因的原假设，表明城镇化地区差距外生于系统，在Granger意义下短期内不影响城镇固定资产投资的地区差距。在我国现实中，中央政府和高层级政府以GDP为导向，在考虑政府投资布局时，各地区城镇化水平的高低并不作为直接的考虑因素。

长期因果关系的判断可以从VECM误差修正项系数的显著性水平来考察。表8给出了两个方程误差修正项的系数值和显著性水平。

可以看出，在10%的显著性水平下，IFA变动都是THL变动的长期Granger原因。在5%的显著性水平下，THL变动是IFA变动的长期Granger原因，说明城镇化水平高的地区，其所能吸引的固定资产投资从长期来说也会很高，尽管这种投资吸引能力在短期内并不明显。这在一定程度上可以体现城市集聚效应所能产生的吸引力的大小，城镇化水平高、集聚效应高的地区，其吸引固定资产投资的能力会更强，下一步大都市圈发展、区域极化发展的趋势可能进一步加强。

结论和建议

本文以利用1978-2011年我国人口输入区和输出区城镇化水平差异与城镇固定资产投资的地区差异为研究对象，通过建立VAR模型，对政府作用效果进行了实证分析。城镇化水平差异和城镇固定资产投资差异具有长期协整关系，不同地区的非均衡投资政策是城镇化区域差异的长期原因。政府主导对不同区域的非均衡投资，将会扩大区域间城镇化水平的差异。基于VECM的Granger因果关系表明，城镇固定资产投资地区差距是城镇化地区差距的短期和长期Granger原因，城镇固定资产投资地区差距的扩大，将会导致城镇化地区差距的扩大。而在短期内，城镇化地区差距不是城镇固定资产投资地区差距的Granger原因，不会影响城镇固定资产投资的地区差距。但在长期内，城镇化地区差距将会影响城镇固定资产投资的地区差距，说明城镇化水平高的地区其所能产生的集聚效应将会吸引更多的投资。

以上研究结论对于我国实现新型城镇化、缩小城镇化的区域差距具有以下启示：首先，要实现城镇化区域间的均衡发展，政府必须调整区域发展政策，各个区域在固定资产投资及其配套的财税、金融政策要均等化，避免地区差距进一步拉大；其次，为缩小中部和西部在城镇化水平上同东部的差距，中央政府可针对性地加大对中部和西部地带的投资比重，使后进地区能够在较短时间内追上先发地区；最后，城镇化水平较高的地区对固定资产投资具有较大的吸引力，下一步我国城镇化很有可能会出现区域极化的现象，特大型、超大型的都市圈和区域核心城市将会出现，国家在宏观政策层面上需要早作应对。

参考文献：

1.经济增长前沿课题组.经济增长、结构调整的累积效应与资本形成［J］.经济研究，2003（8）

2.李庆云.真心实意做好城镇化的大文章［J］.中国经济，2011（2）

3.刘玉.中国流动人口的时空特征及其发展态势［J］.中国人口·资源与环境，2008（1）

4.鲁奇，王国霞等.流动人口分布与区域经济发展关系若干解释（1990、2000）［J］.地理研究，2006（5）

5.马忠东，王建平.区域竞争下流动人口的规模及分布［J］.人口研究，2010（3）

6.宋丽智.我国固定资产投资与经济增长关系再检验：1980-2010年［J］.宏观经济研究，2011（11）

7.王小鲁，樊纲.中国地区差异的变动趋势和影响因素［J］.经济研究，2004

8.中国发展基金研究会.促进人的发展的中国新型城镇化战略［M］.人民出版社，2010

9.高铁梅.计量经济分析方法与建模（第二版）［M］.清华大学出版社，2009

中图分类号：◆F812.45

文献标识码：A