基于多选项二次联合背包的态势感知资源分配算法

孙岩炜，郭云川，张玲翠，方滨兴

(1.中国科学院信息工程研究所信息安全国家重点实验室，北京 100093；2.东莞电子科技大学电子信息工程研究院，广东 东莞 523808)

基于多选项二次联合背包的态势感知资源分配算法

孙岩炜1，郭云川1，张玲翠1，方滨兴2

(1.中国科学院信息工程研究所信息安全国家重点实验室，北京 100093；2.东莞电子科技大学电子信息工程研究院，广东 东莞 523808)

为了有效应对潜在网络威胁，通过合理利用资源达到最大化提升当前环境安全态势的目的，研究了有限资源的最优分配方案。网络态势的整体性特点使针对某一指标的改善可能会间接影响其他指标，并且投入力度不同，影响程度也有所差异。针对上述特性，将问题抽象成多选项二次联合背包模型，通过二次背包特性表示态势评估指标项之间的相互影响，通过多选项背包特性来表示单个指标项的多种投入可能。最后对其做半定规划松弛，采用分支定界法对问题进行求解。实验证明了算法的准确性和高效性。

资源分配；态势感知；多选项二次联合背包；半定松弛

1 引言

态势感知的定义最早由Endsley在1988年提出，强调在一定的空间和时间范围内对环境中元素的获取和理解，并且对未来的状态进行预测。随后在1995年又提出了态势感知模型[1]，如图1所示。该定义被应用到网络中，引起了众多学者的注意，近年来，涌现出了大量的研究文献，研究内容主要包括数据采集[2]、数据融合[3,4]、未知异常检测[5]和态势可视化展示[6]等，而对用户进行决策支持的研究则相对较少。正如Tadda等[7]的阐述，目前态势感知的讨论还仅局限于某一个特定的时间点。理想化的模型应像Webb等[8]提出的，分析当前网络环境态势，产生相应的措施，态势受措施影响，进而形成新的态势，如此循环往复。由此可见，决策支持模块的研究，是保证整体态势感知实时性的关键。

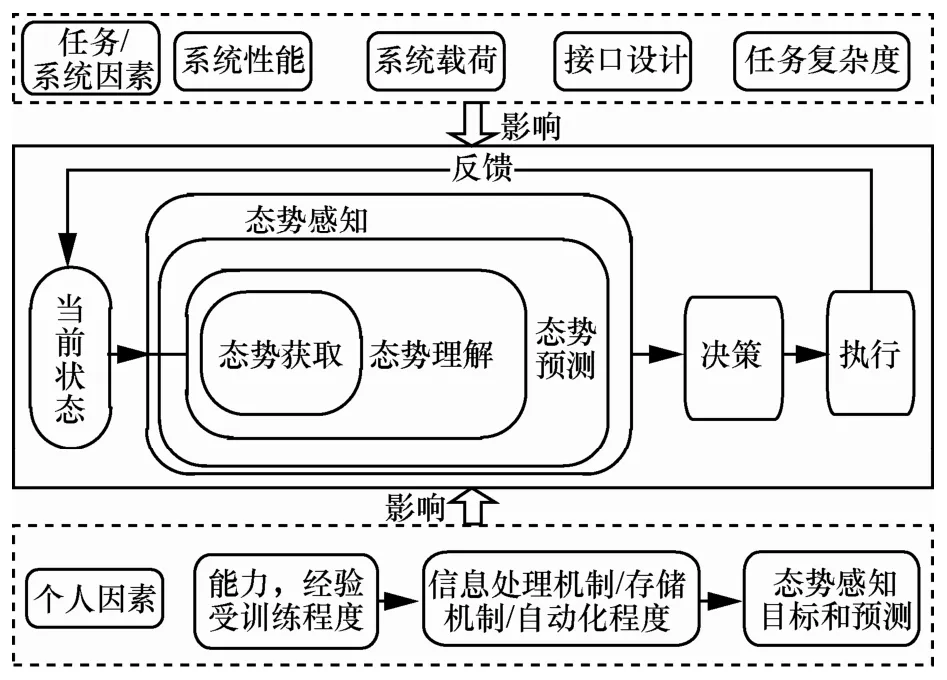
图1 态势感知模型

依照ISO27001、NIST SP800等现有的风险评估准则，以及细化的安全评估指标子项[9]，用户很容易将当前环境的各个指标进行量化考核，最终加权得到整体的态势评估结果。但是面对亟待改进的指标子项以及受限的资源总量，如何将资源在指标子项之间进行分配，从而最大化地提升整体的态势评估结果，是一个复杂的规划问题。因为态势是一个整体的概念，各指标子项之间存在着相互的影响关系，牵一发而动全身。例如，通过态势评估，发现某些关键区域缺乏管理和监督，并且工作人员安全意识不足。针对此情况，如果投入大量资源，加大人员考核力度和监管力度，虽然在一定程度上有利于员工提升自己的安全意识，但同时对员工的过分监督、怀疑与不信任，也会产生不可忽视的社会心理学问题[10]，员工有可能表现出消极怠工甚至报复的行为，即对态势的其他指标子项产生负面影响。正是由于这些错综复杂的关联关系，管理者面对大量有待改进的指标子项，即使有很多改进手段，但容易因考虑不周投入不适当而造成资源的不均衡分配，使最后收益甚微。

面对大量的指标子项，如何分配有限的资源使收益最大化，是典型的背包问题。虽然背包问题有很多种变形，而且相应的算法也很成熟，但是应用到态势感知环境下，依然有一些问题没有得到很好的解决。首先，本场景指标子项之间存在相互影响，并且不同的投入力度，其影响程度也有所差异，目前，尚无任何一个模型能够很好地模拟上述特性；其次，目前，有关背包问题的研究，随着投入的增长，对应的产出是单调递增的，而本场景可能存在产出不增反降的情况，目前，针对此情况的求解研究十分有限。

针对上述两点，本文的主要贡献如下：将二次背包问题与多选项背包问题相结合，提出了多选项二次联合背包模型（MCQKP,multiple-choice quadratic knapsack problem），从而很好地解决了态势感知环境下的资源分配问题；在求解问题时，考虑了收益矩阵元素取值为负的情况，给出了半定规划松弛的求解方法。

2 相关工作

随着应用背景的不同，资源分配方法存在巨大差异，根据资源分配模型中参与方的数量差异，可大致分为如下3种：只有单方参与的资源分配问题、双方参与的资源分配问题以及多方参与的资源分配问题。

单方参与的资源分配问题主要应用在云计算、通信网络数据传输、网络防护措施选择等方面，这类问题可简单概括为：在满足一定限制的前提下，使参与方的收益最大化或者损失最小化。如果收益函数是线性的，则可用典型的背包问题求解，如果是非线性的，则可以通过取对数等方式将问题线性化之后求解[11]，或采用典型的数据分组分析模型进行分析[12]。Aisopos 等[13]通过背包模型，将云计算中需要的内存、硬盘、CPU资源进行综合考虑，并且根据用户需求碎片化的特点，将多重背包问题进行了整数松弛，使整个求解过程的时间复杂度大大降低。Xiao 等[14]的研究目的并非收益最大化，而是在满足虚拟机需求的前提下，尽可能减少工作实体机数量，从而达到节约资源的目的。另外，通信过程中的带宽分配，也经常用线性规划模型来处理。Hajiaghajani等[15]讨论终端对终端通信的过程，在保证服务质量的前提下，使最大速率(sum-rate)最大化。Ferdosian等[16]将背包算法用在LTE技术当中，在带宽有限的前提下，通过评估量化，选取用户的一个子集提供服务，从而实现系统性能的最大化。同样受限于带宽，Sheu等[17]讨论无线城域网的资源分配问题，力求通过合理分配带宽，使网络吞吐量达到最大化，同时使受众用户数量最大化。

涉及双方参与的资源分配问题，最典型的研究是基于博弈论的资源分配方法。这类研究在网络攻防领域应用十分广泛，主要是通过计算纳什均衡，来指导管理员对资源的分配。例如，Fielder等[18]通过模拟攻防双方的零和博弈，算出混合策略下的纳什均衡，从而指导用户进行资源分配优化。Khouzani 等[19]在考虑威胁动态转移时，同样通过博弈论的方法，计算帕累托最优，进而计算系统损失的最小值。同样在资源受限的前提下，Ojamaa等[20]通过离散动态规划，计算帕累托最优方案，对用户进行决策支持。

涉及多方参与的资源分配问题，主要应用在云计算、设备到设备（D2D）通信等环境，普遍采用博弈论下的拍卖模型对问题进行模拟和求解。在D2D通信背景下，Wang等[21]提出迭代联合拍卖算法，通过功率控制和联合信道管理，有效提高用户设备的续航能力。Hasan等[22]通过拍卖的方法，研究多层异构网络下的频率、时隙等资源的合理分配。有关云计算下的资源分配，Zhang等[23]针对用户需求的异构性，提出了一种新的竞标表述方式，并且构建了具有激励机制的在线云资源拍卖机制。

结合上述分析，由于本文研究的目的旨在利用有限资源最大化提升当前环境的安全态势，并未涉及攻击方，以及其他多方参与的情况，因此，本文研究单方参与的关于网络安全防护的资源分配问题。与本文类似的研究还包括：Gupta等[24]考虑网络风险与相应策略之间的关系，假设针对每一个潜在的风险，都会有一个补救措施与之对应，但同时该措施可能会引起其他方面的新风险产生，于是措施选择问题便转化成了最小覆盖的问题。虽然考虑了风险与措施之间的相互影响，但是在建模时将问题进行了简化，针对某一个风险，只设定了解决、未解决和部分解决这3个状态，这使其决策支持算法的计算量大大降低。在它的基础上，Viduto 等[25]还考虑了投入成本的限制因素；Schilling等[11]从德国联邦信息安全办公室获取到大量有价值的安全数据，从中提取出500多项威胁以及1 200多项应对措施，以网络组件为单位，计算威胁值。Rees等[26]主要对收益、损失等参数进行了讨论，通过模糊集理论来处理风险管理当中的不确定性。Sawik等[27]在评估风险时用到了风险价值和条件风险价值这2个指标方法。Mukhopadhyay 等[28]通过基于耦合的贝叶斯信念网络对网络风险进行评估和量化，并且根据不同的需求以及有限的投入资源，动态调整决策支持方案。Gordon等[29]将风险与投入进行分级讨论，针对不同的安全风险等级，计算相对应的最优投入策略。

虽然文献[11,24,25]做了内容类似的研究，在选择防护措施时考虑到了整体性特点，提出了防护措施与安全威胁之间多对多的映射关系，但作者在选择措施时均只考虑选与不选2种可能，并没有考虑实施力度的差异，因此，上述研究均有不同程度的局限性。为了克服上述局限，本文采用二次背包模型对问题进行模拟，同时为了使本文的研究更加贴近实际，对问题进行了扩充，目前已有的关于二次背包及其变形[30～32]均已无法满足需求，因此，本文提出了新的背包模型——多选项二次联合背包。

3 多选项二次联合背包问题模型

首先对应用场景进行描述，指出目前研究的不足，接着通过示例引出问题的数学表示，并对问题当中的参数及合理性做了简单讨论，最后提出多选项二次联合背包模型的数学表述。

3.1 问题描述

在描述问题之前，先给出指标子项以及投入子项的定义，接着给出态势环境下的背包问题的定义，并且通过逐步引入限制条件，指出目前研究存在的不足。

定义1指标子项。当前环境下，将影响整体态势的每一个环节，细分为可供评估的若干个指标项，称之为指标子项，如系统顽健性这个环节包含管理员密码修改频率是否达标、服务器代码是否包含容错处理和系统内部是否开启不必要的服务等指标子项；项目及人员管理环节包含特定操作是否有配套规范守则、人员是否遵守、是否有专人监督和是否定期开展人员安全意识考核等子项。每一个指标子项用INDn表示。

定义2投入子项。态势评估结果中未达标的指标子项，即需要投入一定资源进行改善的指标项。投入子项用INVn表示，每个投入子项包含2个属性：改善所需资源消耗ri和改善后带来的评估提升值pi（相关参数将在3.2节做简单讨论，而具体的资源消耗与提升函数关系的讨论，超出了本文的研究范围，在这里只做简单的假设）。

定义3态势环境下的背包问题。在投入资源总量受限的条件下，如何选取投入子项进行资源分配，使在不超过总资源限制的前提下，达到评估提升总和最大，这是态势环境下的背包问题。图2以柱状图的形式描述该问题，针对每一个指标项，其高度表示态势评估值大小，虚线框表示对该项指标进行投入时所获得的态势收益提升，箭头虚线表示一种可行的分配方案。

图2 简单资源分配

在上述问题的基础上，考虑项目之间存在相互影响的情况。如根据态势评估结果，需要在人员培训、人员考核等子项投入资源，最直接的表现是每个投入子项获得相应的评估值提升。同时，人员培训还有助于提升员工自身的安全意识，从而在其他工作，如代码质量方面、密码强度方面和应急响应方面有间接的提升。但是，加强监督力度等措施，会对工作人员的心里产生不可忽视的影响，甚至产生报复心里，恶意破坏系统内部的正常工作。在本例中的直接体现即对一些特定项产生负收益，资源分配图示如图3所示。与图2相比较，负收益通过实线箭头表示(图中部分表示简化为pxx)。

从图3可以看出，在投入第2项的时候，除了会获得自身的收益p22之外，其他项的收益也会受到相应的影响，如图3中p21、p23等。但是，与二次背包问题不同的是，这里的相互影响是“静态”的，只要对人员培训进行投入，那么与其相关联的p21、p23等就会出现。在这种情况下，只要将问题中的pi稍作调整，即，其中，m为受影响项个数，pii表示投入项i本身的收益，pij表示投入项i对子项j的间接影响收益。经过转化之后，问题还是可以顺利转化为简单的背包问题。

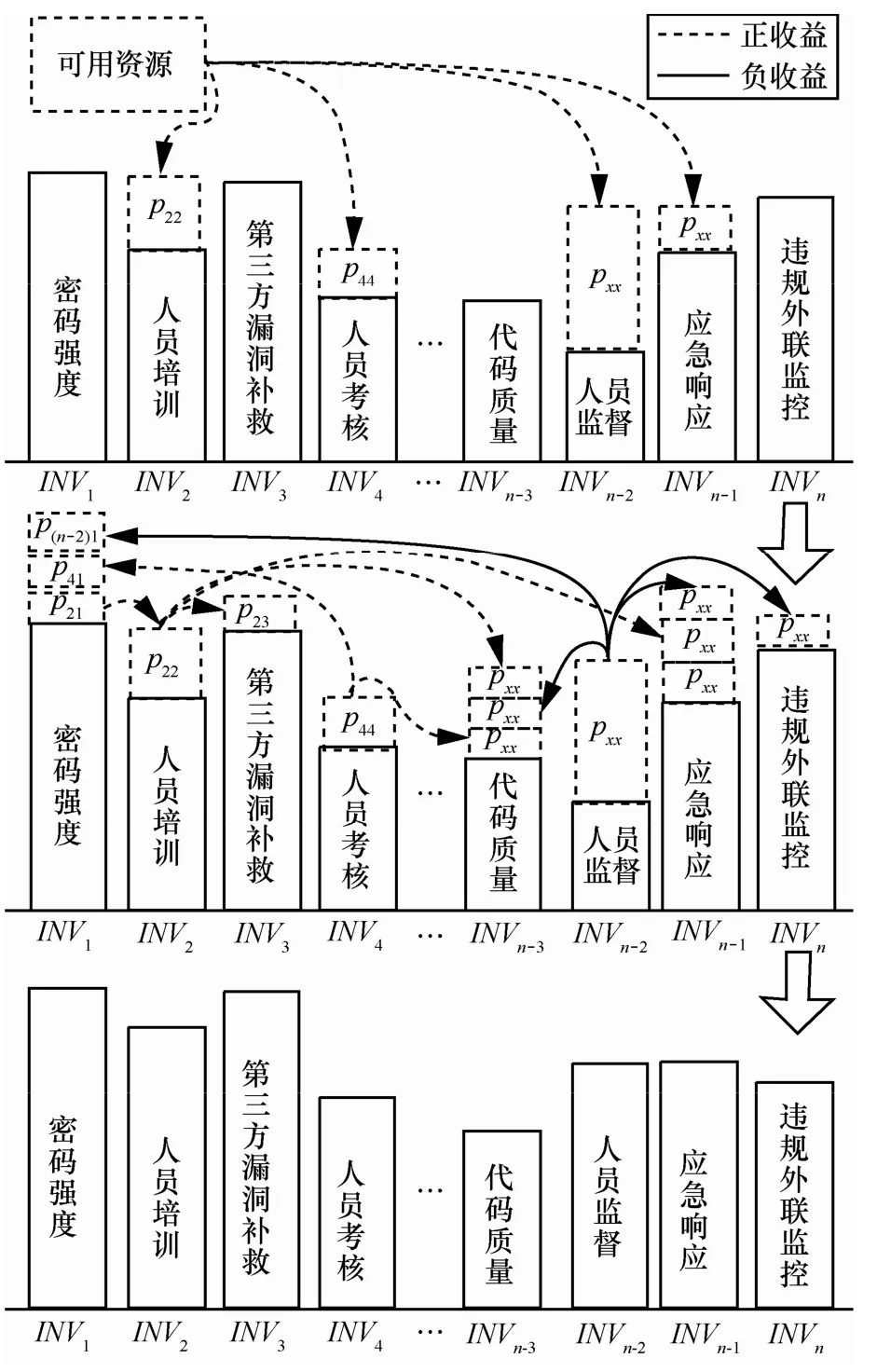
图3 考虑相互影响的资源分配

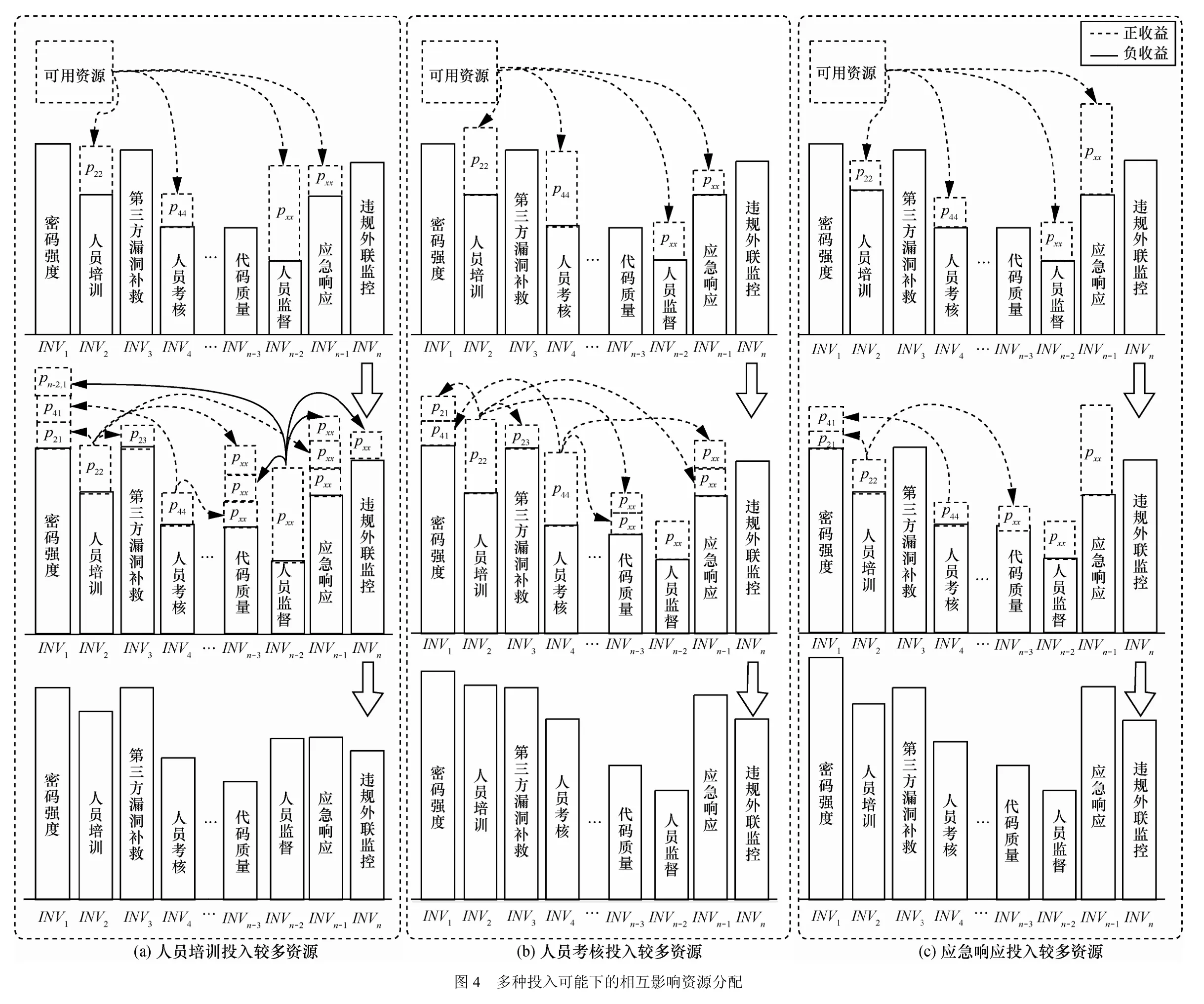
上面的讨论针对某一个投入项i，只有投入与不投入2种情况。而实际中往往每一项i可以有多种投入选择，即可以选择投入ri1,ri2,…,rin的资源，同时，其相对应的收益也会存在不同，即。这个问题下的相互影响，已经不再是“静态”影响，而是会随着投入的多少发生改变，同样的投入子项，不同的资源分配，往往会导致大不相同的提升结果。例如，适度对人员监督子项进行投入，会获得较为理想的正收益，如图4(c)所示，但是如果过度投入，则会对其他子项产生负面影响，如图4(a)所示。在这种情况下，现有模型已经无法满足求解需求，因此，本文提出了多选项二次联合背包模型。

3.2 多选项二次联合背包模型参数讨论

受二次背包问题的启发，本文通过二维矩阵表述指标子项之间的相互影响收益，本文统称为收益矩阵Λ。其中，对角线上的元素表示自身收益，其余元素表示相互影响收益；由于每个子项存在多种投入可能，并且每种投入对其他子项的影响也存在差异，故矩阵当中的每个元素通过4个角标进行描述，其中，pij,kl表示第i项投入j时对第k项投入l时的影响收益，*表示不允许出现的数[33]。

通过一个简单的例子介绍收益矩阵（为了介绍方便，下述实例并不考虑资源总量的限制）。假设目前可供投入的子项只有人员考核、人员监督和人员培训3项，每一项可以有投入值为0、1和2这3种选择。根据定义可以得到如下收益矩阵Λ为

假设投入方案为：对人员考核这一项投入值为1，人员监督投入2，对人员培训不进行投入，通过0−1向量α表示投入方案，此方案可以通过如下向量表示为

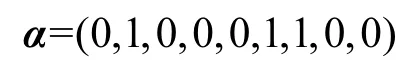
同时，此分配方案对应的总收益为

收益矩阵中的元素pij,kl取值，可参见文献[9]等，本文只对其合理性做简单讨论。

1) 矩阵中的元素，如果i=k则j=l,即不存在p11,22等元素，在矩阵中用*表示。在上述实例中，即不存在人员考核子项投入1对人员考核子项投入2造成的影响。

2) 针对矩阵当中的元素pij,kl，当j为0，l取任意数时，根据定义可得pij,kl的取值为0，对应上例中的p30,11、p30,22等元素，即投入为0的子项i对其他任何子项的影响为0。但是它关于主对角线位置对称的元素pkl,ij在上述情况下，却可能存在不为0的情况，对应上例中的p11,30、p22,30等元素，所以本矩阵严格意义上并非对称矩阵。但是，可以将关于主对角线位置对称的两两元素取平均值，人工将矩阵对称化，这样做的目的是方便后续计算，同时不影响计算结果，详细证明见命题1。

3) 如果i和k保持不变，j和l的任意变化，都会使影响因子产生变化。

命题1在求解收益最大化的过程当中，对于任何一个收益矩阵Λ，在不影响计算结果的前提下，都可以化为一个等价的对称收益矩阵Λ。

证明假设原始收益矩阵Λ中的元素用pij,kl表示，新建对称矩阵 ′Λ中的元素用pi′j,kl表示，令

从上面的表述中可以看出 ′Λ是对称的。现在要证明Λ和 ′Λ具有相同的最优分配方案。设∗α为原始收益矩阵Λ的最优分配方案，即

则总的收益提升P可表示为

从上述等式变换可以得知，矩阵Λ的最优分配方案α∗同时也是对称矩阵Λ′的最优分配方案，因此，将矩阵进行对称化处理，并不影响最优分配方案，故命题得证。

3.3 多选项二次联合背包模型数学表述

通过上面的描述，最终可以得到多选项二次联合背包的数学抽象。

假设共有n个物品被分为m个相互独立的分组：Ν1,…,Nm，每一个物品j∈Ni，重量为wij，Λ为n×n矩阵，其中，pij,ij表示第i组第j个物品被选中所获得的收益。另外，pij,kl+pkl,ij表示第i组第j个物品与第k组第l个物品同时选中时所产生的额外收益，背包总容量用c表示。同时出于书写以及计算方便，本文规定pij,ij′=0 (其中j ≠ j′)。多选项二次联合背包（MCQKP）模型可以表述为

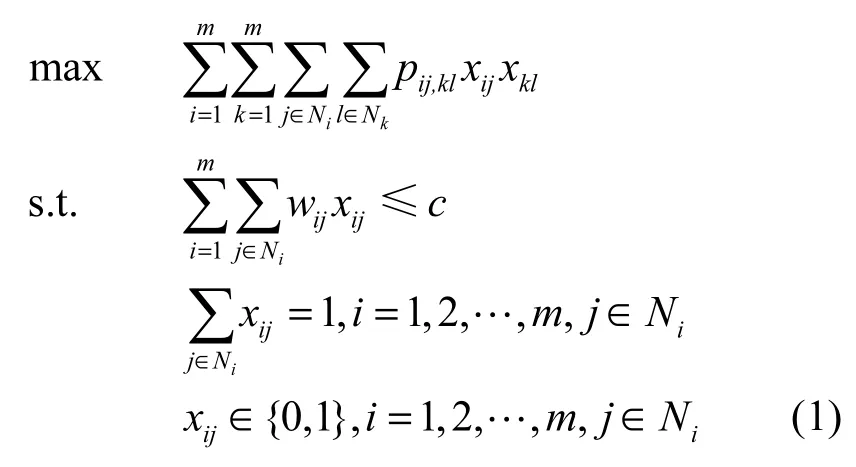
可以看出，该问题是NP难题，因为如果去掉约束条件(1)，问题便转换为了一般的二次背包问题，而二次背包是NP难题的。另外，与大部分的研究不同，从实际情况出发，本模型并没有限定矩阵Λ当中的元素的取值为非负。

需要指出的是，从MCQKP的数学表述上来看，它与广义二次分配问题[34]的表述是极为类似的。但是，二次分配问题的定义，是将M项任务分发给N种可能的设备去处理，其资源消耗矩阵表示如下。

根据定义以及矩阵表述可以看出，二次分配问题当中的每一项任务M都对应相同数目N的分配可能。对应背包问题，它等同于要求每一个分组内的物品数目均相同，这显然是有局限性的，所以本文阐述的背包模型，在适用范围上要优于目前已有的广义二次分配问题。

4 多选项二次联合背包问题求解

对于背包类的NP问题求解，可分为近似解与精确解两大类，本文所提的解法属于精确解。针对背包问题的精确求解，目前已有较为普遍的解决方案CPLEX Optimization Studio，但是受限于其计算问题上界时松弛程度较大，它无法快速地求解这类NP问题，尤其是当计算规模大于一定规模的时候，求解时间将超过1 h甚至更长时间。虽然所有精确解在计算NP问题时的时间复杂度均为指数级，但是计算不同精确度的上界，对于整个计算时间的影响十分明显。因此，本文借鉴已有研究，对问题进行了半定松弛，通过松弛求解出相比于CPLEX更为精确的上界，并通过启发式方法求得问题的下界，最后通过分支定界法对问题进行精确求解。

4.1 通过半定松弛求解问题上界

根据文献[35]提出的QCR方法，本文对MCQKP同样做了半定松弛，表述如下。

上述问题可以通过CSDP注1：该工具可在网站http://www.coin-or.org/获取。等已有的求解工具进行求解，求解时间也较为理想，相关证明以及求解方法参考文献[35]，在此不做过多论述。

4.2 通过启发式算法计算问题下界

算法参照文献[36]中介绍的计算下界的启发式方法，但是由于本问题的分组特性，需要在原方法上加以修改，具体计算步骤如下。

1) 计算问题当中每一个分组i里面收益最高的子项，，并置xij=1。

3) 逐个遍历集合{xij|xij=1}中的每一个元素，缩小j的值，重新计算，并记作Plow′；选取使ΔPlow=Plow–Plo′w最小的xij变换，即xij置0，xij′置。重复此过程直到W≤c时结束。至此，算法已得到了问题的一个下界Plow1。

4) 继续对Plow1进行优化。依次遍历集合{xij|xij=0}的部分，如果xij子项可以直接投入所需资源而没有超过总限制，则将ΔPijlow记录为投入该子项所获得的利益增量。如果无法直接投入，在不超过总资源的基础上，将该子项与已投入的子项依次轮换，将 ΔPijlow记录为收益增量的最大值。选取每一个ΔPijlow当中的最大值进行置换，重复此步骤，直到ΔPlow为0时停止，这样算法就得到了一个较为优质的下界。

4.3 通过分支定界法求解问题的最优解

在得到问题的上界和下界之后，可以用经典的分支定界法对问题进行求解，相关求解的方法在文献[36]中已有较为详细的论述。

5 实验环境与结果分析

5.1 实验数据及环境

本文在Windows 8系统下进行独立性能测试。测试机配置为Intel Core i3-3240 3.4 GHz处理器，6 GB内存，其中，CSDP算法采用ECLIPSE集成CSDP-6.1.1进行计算处理， ECLIPSE分配的虚拟内存为2 GB；CLPEX运行环境为CPLEX Optimization Studio Community Edition 12.6。

本文从文献[9]中提取了30组指标子项，规定其中10组指标子项可投入选项为4项，其余20组指标可投入选项为3项，生成了100×100的收益矩阵Λ。其中，子项之间的相互影响根据文献[3,37]当中的威胁与防护措施之间多对多的映射来生成。表1列举了部分措施所对应的威胁数目以及可能引起的负面影响数目。

表1 防护措施与威胁对应关系

具体的各个子项的量化结果，文献没有介绍，用户可以根据每项指标的重要程度差异，来量化投入资源到该子项时所能获得的收益提升。实验假设整体态势的最优值为100，前10项指标项的投入收益p（包含自身收益以及与其相关的所有间接收益）的范围是0～4，后20项投入收益p的范围是0～3。

5.2 实验高效性结果分析

首先进行运行时间的对比，通过随机生成不同规模的收益矩阵，规定其矩阵密度δ=90%，将矩阵同时放在CPLEX 12.6 Community Edition环境与半定规划算法进行运算，运行时间上限定为1 800 s，二者的运行时间对比如图5所示。

图5 算法运行时间随收益矩阵规模变化趋势

从图5中可以看到，在规模较小的情况下，二者的运行时间差异并不明显，在CPLEX环境下，运算时间在矩阵规模达到30之后开始急剧增多，在矩阵规模达到50时，已经无法在1 h内求得精确解；而采用半定规划求解时，当规模增加到100时，其运行时间仍在650 s左右，其1 h内能够计算出的最大矩阵规模达到125；造成差距如此巨大的一个原因，是由于CPLEX对于问题上界求解的松弛度较高，因此未能有效地缩小枚举范围，为了有效地衡量二者在计算上下界时的差异，，松弛度越小，表明上下界贴合越接近，搜索空间越小。表2列出了2种算法松弛度的差异，从表2中可以看出，CPLEX计算的松弛度平均值达到80.9%，而半定规划的松弛度平均值只有22.26%。

5.3 实验准确性结果分析

出于最优化计算结果的对比，除了本文提出的多选项二次联合背包模型之外，还计算了经典背包分配方案[38]和二次背包[39]分配方案。其中，经典背包分配方案在计算时只考虑主对角线元素，而忽视指标项之间的相互影响。二次背包分配方案只考虑投入与不投入2种情况，并不考虑多种投入可能。

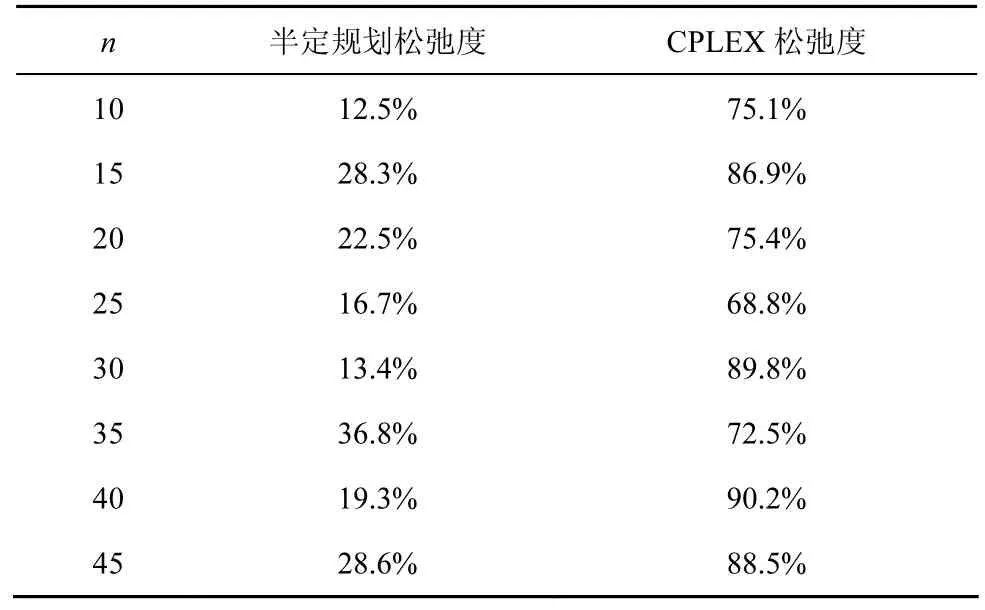
表2 2类解法松弛度比较

图6是3种方案的态势评估总收益P随着投入资源总量变化的曲线，可看出，给定任意数量的资源限制，多选项二次联合背包模型分配方案获得的收益都是最大的，而且随着投入数目的增加，其优势表现得越明显，因为资源投入越多，其投入的子项数量也相应增多，子项间的相互影响越发明显，在投入接近140时，收益达到最大值100，而其他2种方案的最大值在90附近。值得注意的是，经典背包方案在投入总量为140附近的时候，出现了态势评估收益随投入增加而下降的情况，造成这一现象的原因是各子项之间存在抑制影响，而经典背包方案在考虑资源分配时并没有兼顾此类影响，致使出现投入增加而收益下降的情况出现。

图6 态势评估收益随总投入变化

图7是3种分配方案的投入产出比，表示在某一固定投入总量的情况下，单位资源所能获得的态势评估收益。由于某种方案在某些特定的投入总数限制下，可能存在资源有剩余的情况，所以实际的投入产出比与总收益的曲线趋势并不完全一致。从图7中可以看出，随着投入增多，单位资源所能获得的平均收益均为下降趋势，这是由于在资源总量很少的情况下，要想获得最大化的收益提升，必然要把有限的资源投入到性价比最高的子项当中，随着投入总量的增加，单位资源所能获得的收益提升也随之降低。经典方案之所以起点较低，同样是因为没有考虑子项之间存在的影响收益，单纯地选取自身收益最高的子项先行投入，另外2种方案则选取自身收益与影响收益总和最高的子项进行投入。但是二次方案没有考虑投入的多力度性，在资源总量25附近出现了大幅波动，因为资源总量较少时，二次方案容易出现资源的不完全利用，即并没有把25的资源全部有效分配，而由于方案考虑的力度过大，剩余资源不足以完成分配，直到总量增加，新增资源与之前的剩余资源足够进行下一次分配，其收益才会有跳跃式增长。

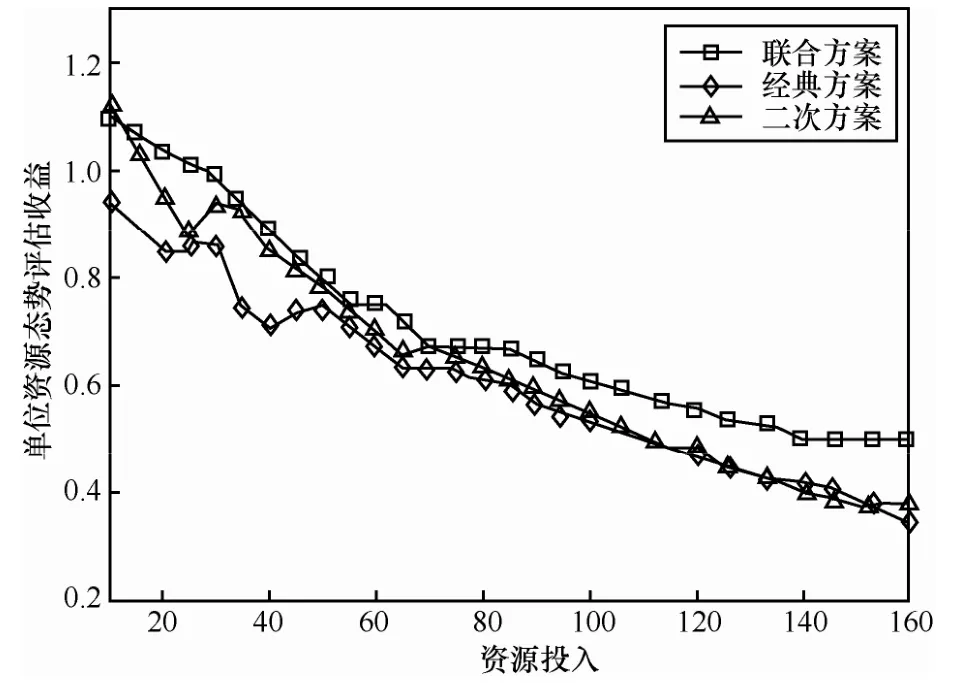
图7 单位资源态势评估收益随总投入变化

图8是算法规定投入总数为100的时候，30项指标的投入情况，受到条件限制，二次方案曲线浮动较为明显，相比之下，另外2种投入方案的浮动较为平缓。联合方案的投入多集中在中线附近，表明投入较为平均。

图8 指标子项投入明细

与图8相对应，图9是算法规定投入总数为100的时候，30项指标的提升情况。以联合方案的指标提升值的升序顺序进行展示，由于投入资源的差异，各项指标的提升差异较为明显，但是联合方案的各项提升较为平均，更加符合态势的整体性特点，同时整体水平也高于其他2种方案。

图9 指标子项态势评估值提升明细

6 结束语

网络安全态势感知虽然受到广泛关注，但是绝大部分研究都聚焦于问题的发现和态势的展示，决策支持方面的研究则相对较少。在发现威胁以后，如何利用有限的资源最大化地消除隐患，提升当前环境的安全态势，是一个复杂的规划问题。因为态势是一个整体的概念，各子项之间存在着相互的影响关系。根据该特点，本文将问题抽象成为一种新的背包模型，即多选项二次联合背包，并对其进行了半定规划松弛，采用分支定界法对问题进行求解。最后通过模拟实验，证明了本算法的分配方案，要优于目前已有的二次背包分配方案以及经典背包分配方案。

[1]ENDSLEY M R.Toward a theory of situation awareness in dynamic systems[J].Human Factors:The Journal of the Human Factors and Ergonomics Society,1995,37(1):32-64.

[2]DIETTERICH T G,BAO X,KEISER V,et al.Machine learning methods for high level cyber situation awareness[M]//Cyber Situational Awareness.Springer US,2010:227-247.

[3]LIU P,JIA X,ZHANG S,et al.Cross-layer damage assessment for cyber situational awareness[J].Advances in Information Security,2010,46:155-176.

[4]PREDEN J,MOTUS L,MERISTE M,et al.Situation awareness for networked systems[C]//2011 IEEE International Multi-Disciplinary Conference on Cognitive Methods in Situation Awareness and Decision Support (CogSIMA).IEEE,2011:123-130.

[5]BRANNON N G,SEIFFERTT J E,DRAELOS T J,et al.Coordinated machine learning and decision support for situation awareness[J].Neural Networks,2009,22(3):316-325.

[6]TAMASSIA R,PALAZZI B,PAPAMANTHOU C.Graph drawing for security visualization[C]//International Symposium on Graph Drawing.Springer Berlin Heidelberg,2008:2-13.

[7]TADDA G P,SALERNO J S.Overview of cyber situation awareness[M].Cyber Situational Awareness.Springer US,2010:15-35.

[8]WEBB J,AHMAD A,MAYNARD S B,et al.A situation awareness model for information security risk management[J].Computers &Security,2014,44:1-15.

[9]Federal Office for Information Security:13 EL:Cross-reference tables of the IT-grundschutz catalogues:13th version (2013).[EB/OL].https:// http://enos.itcollege.ee/～valdo/bsieng/en/gstoolhtml/allgemein/vorwort /00001.html.

[10]GREITZER F L,FRINCKE D A.Combining traditional cyber security audit data with psychosocial data:towards predictive modeling for insider threat mitigation[M]//Insider Threats in Cyber Security.Springer US,2010:85-113.

[11]SCHILLING A,WERNERS B.Optimizing information systems security design based on existing security knowledge[C]//International Conference on Advanced Information Systems Engineering.Springer International Publishing,2015:447-458.

[12]DU J,COOK W D,LIANG L,et al.Fixed cost and resource allocation based on DEA cross-efficiency[J].European Journal of Operational Research,2014,235(1):206-214.

[13]AISOPOS F,TSERPES K,VARVARIGOU T.Resource management in software as a service using the knapsack problem model[J].International Journal of Production Economics,2013,141(2):465-477.

[14]XIAO Z,SONG W,CHEN Q.Dynamic resource allocation using virtual machines for cloud computing environment[J].IEEE Transactions on Parallel and Distributed Systems,2013,24(6):1107-1117.

[15]HAJIAGHAJANI F,RASTI M.Downlink resource reuse for device-to-device communication underlying cellular networks using a generalized knapsack framework[C]//2016 13th IEEE Annual Consumer Communications &Networking Conference (CCNC).IEEE,2016:171-176.

[16]FERDOSIAN N,OTHMAN M,ALI B M,et al.Greedy–knapsack algorithm for optimal downlink resource allocation in LTE networks[J].Wireless Networks,2015:1-14.

[17]SHEU J P,KAO C C,YANG S R,et al.A resource allocation scheme for scalable video multicast in WiMAX relay networks[J].IEEE Transactions on Mobile Computing,2013,12(1):90-104.

[18]FIELDER A,PANAOUSIS E,MALACARIA P,et al.Decision support approaches for cyber security investment[J].Decision Support Systems,2016,86:13-23.

[19]KHOUZANI M H R,MALACARIA P,HANKIN C,et al.Efficient numerical frameworks for multi-objective cyber security planning[C]//European Symposium on Research in Computer Security.Springer International Publishing,2016:179-197.

[20]OJAMAA A,TYUGU E,KIVIMAA J.Pareto-optimal situation analysis for selection of security measures[C]//MILCOM 2008-2008 IEEEMilitary Communications Conference.IEEE,2008:1-7.

[21]WANG F,XU C,SONG L,et al.Energy-efficient resource allocation for device-to-device underlay communication[J].IEEE Transactions on Wireless Communications14.4.2015:2082-2092.

[22]HASAN M,HOSSAIN E.Distributed resource allocation in D2D-enabled multi-tier cellular networks:an auction approach[C]// 2015 IEEE International Conference on Communications (ICC).IEEE,2015.

[23]ZHANG H,JIANG H,LI B,et al.A framework for truthful online auctions in cloud computing with heterogeneous user demands[J].IEEE Transactions on Computers,2016,65(3):805-818.

[24]GUPTA M,REES J,CHATURVEDI A,et al.Matching information security vulnerabilities to organizational security profiles:a genetic algorithm approach[J].Decision Support Systems,2006,41(3):592-603.

[25]VIDUTO V,MAPLE C,HUANG W,et al.A novel risk assessment and optimization model for a multi-objective network security countermeasure selection problem[J].Decision Support Systems,2012,53(3):599-610.

[26]REES L P,DEANE J K,RAKES T R,et al.Decision support for cyber security risk planning[J].Decision Support Systems,2011,51(3):493-505.

[27]SAWIK T.Selection of optimal countermeasure portfolio in IT security planning[J].Decision Support Systems,2013,55(1):156-164.

[28]MUKHOPADHYAY A,CHATTERJEE S,SAHA D,et al.Cyber-risk decision models:to insure IT or not?[J].Decision Support Systems,2013,56:11-26.

[29]GORDON L A,LOEB M P.The economics of information security investment[M]//Economics of Information Security.Springer US,2004:105-125.

[30]LÉTOCART L,PLATEAU M C,PLATEAU G.An efficient hybrid heuristic method for the 0-1 exact k-item quadratic knapsack problem[J].Pesquisa Operacional,2014,34(1):49-72.

[31]SHENG H,SUN J,SUN X.A Rigorous method for solving 0-1 polynomial knapsack problem [J].Journal of Shanghai University (Natural Science Edition),2006,4:012.

[32]BRETTHAUER K M,SHETTY B.Quadratic resource allocation with generalized upper bounds[J].Operations Research Letters,1997,20(2):51-57.

[33]HAHN P,GRANT T.Lower bounds for the quadratic assignment problem based upon a dual formulation[J].Operations Research,1998,46(6):912-922.

[34]HAHN P M,KIM B J,GUIGNARD M,et al.An algorithm for the generalized quadratic assignment problem[J].Computational Optimization and Applications,2008,40(3):351-372.

[35]BILLIONNET A,ELLOUMI S,PLATEAU M C.Improving the performance of standard solvers for quadratic 0-1 programs by a tight convex reformulation:the QCR method[J].Discrete Applied Mathematics,2009,157(6):1185-1197.

[36]CAPRARA A,PISINGER D,TOTH P.Exact solution of the quadratic knapsack problem[J].Informs Journal on Computing,1999,11(2):125-137.

[37]ANDERSON R H,FELDMAN P M,GERWEHR S,et al.Securing the US defense information infrastructure:a proposed approach[R].Rand Corp Santa Monica CA,1999.

[38]KELLERER H,PFERSCHY U,PISINGER D.Introduction to NP-completeness of knapsack problems[M].Springer Berlin Heidelberg,2004.

[39]BRETTHAUER K M,SHETTY B.The nonlinear knapsack problem–algorithms and applications[J].European Journal of Operational Research,2002,138(3):459-472.

孙岩炜（1989-），男，山西太原人，中国科学院信息工程研究所博士生，主要研究方向为网络安全。

郭云川（1977-），男，四川营山人，博士，中国科学院信息工程研究所副研究员，主要研究方向为网络与信息系统安全、访问控制。

张玲翠（1986-），女，河北故城人，中国科学院信息工程研究所博士生，主要研究方向为网络安全、信息保护。

方滨兴（1960-），男，江西万年人，中国工程院院士，东莞电子科技大学教授，主要研究方向为计算机体系结构、计算机网络与信息安全。

Resource allocation algorithm for situation awareness based on multiple-choice quadratic knapsack

SUN Yan-wei1,GUO Yun-chuan1,ZHANG Ling-cui1,FANG Bin-xing2
(1.State Key Laboratory of Information Security,Institute of Information Engineering,CAS,Beijing 100093,China;2.Institute of Electronic and Information Engineering,University of Electronic Science and Technology of China in Dongguan,Dongguan 523808,China)

In order to deal with the potential cyber-threat and improve the security situation by using limited resource properly,the optimal allocation of resource focused on cyber security situation.The coherence of network situation lead to the fact that the enhancement of certain item may also affect some other items,and different amount of investment may also result in different degree of impact,therefore,the problem was extracted into the multiple-choice quadratic knapsack problem.The characteristics of quadratic knapsack problem was used to model the interactions among the situation indicator items,meanwhile used the multiple choice knapsack problem to model the multiple investment choice for each item.A branch and bound algorithm was conducted by using the semi-definite relaxation.The experiment results show the accuracy and efficiency of proposed algorithm.

resource allocation,situation awareness,multiple-choice quadratic knapsack,semi-definite relaxation

s:Strategic Priority Research Program of Chinese Academy of Sciences(No.XDA06030200),The National Key Research and Development Program of China (No.2016YFB0800303,No.2016YFB0800700),Core Electronic Devices,High-end General Purpose Chips and Basic Software Products (No.2015ZX01029101),The Industry-University-Research Cooperation Project of Guangdong Province (No.2016B090921001)

TP301

A

10.11959/j.issn.1000-436x.2016272

2016-08-11；

2016-11-01

郭云川，guoyunchuan@iie.ac.cn

中国科学院战略先导专项基金资助项目（No.XDA06030200）；国家重点研发计划基金资助项目（No.2016YFB0800303,No.2016YFB0800700）；核高基基金资助项目（No.2015ZX01029101）；广东省产学研合作基金资助项目（No.2016B090921001）