模拟淘汰程序的设计方法研究——以“猴子选大王”程序为例

王　胜

（犍为外国语实验学校，四川　犍为　614400）



模拟淘汰程序的设计方法研究
——以“猴子选大王”程序为例

王胜

（犍为外国语实验学校，四川犍为614400）

摘要：猴子选大王是一道经典的程序设计题，文章指出，可以通过不同的设计方法来实现：（1）模拟数组法。（2）模拟链表法。（3）stl l ist实现。（4）数学推导法。

关键词：猴子选大王；模拟；链表；stl l ist；数学推导

问题：n只猴子围成一个圈。从第一只猴子开始，从1开始依次报数，报到m的猴子离开。从这只离开猴子的下一只开始再从1开始报数，报到m的再离开。以此类推，直到最后剩下一只猴子为止。这只剩下的猴子就是大王。现在编写程序，输入n和m，输出大王的号码。

1　模拟静态数组法

学习了静态数组后，可以直接用静态数组来模拟淘汰的过程。

原理：设置n+1数组，初值为0，表示n只猴子都在圈子里，淘汰的猴子赋值为1。从数组1开始扫描，查看对应的值是否为0并计数，扫描到m个0后，把对应数组的值修改为1，表示淘汰。继续执行下一步的操作，直到里面只剩下一只猴子结束。最后从1开始扫描数组，找到一个为0的结束，该下标对应的猴子为大王。关键：0，1表示猴子是否在圈中，扫描的时候忽略不在的猴子，设置结束标记，能正常结束。

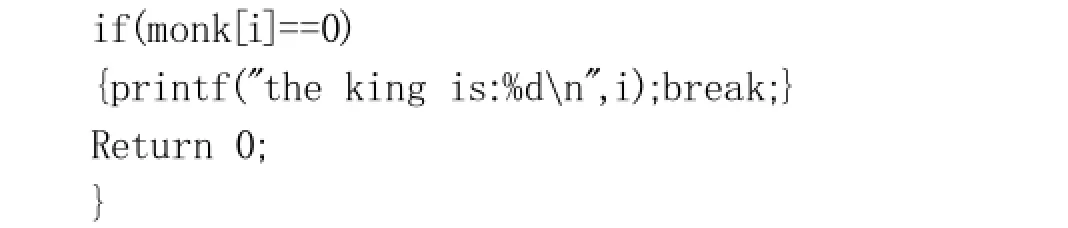
优点：理解容易，代码较易实现。

缺点：效率差，每次都要扫描全部的数据，还要判断该位置上是否有猴子。对于大一些的数据运行时间长。

2　模拟链表法

数组法在淘汰过程中要不断判断对应的值是否为0，即猴子是否在圈内，扫描判断效率低。学习链表后，我们可以用环形链表实现，每个节点代表一个猴子，扫描淘汰过程中直接删除该结点，避免了判断及重复扫描浪费时间。

优点：执行效率比数组高，只扫描不判断，提高了运行时间，临时开辟存储空间，不用预先定义避免了内存浪费。

缺点：链表理解编写有一定的难度。

3　stl list实现

自从有了stl后，可借助里面的容器list（链表）快速实现链表功从而进行程序设计及代码的编写。解题思路：生成一圈猴子，边扫描边删除，快速模拟淘汰过程。

优点：代码简洁，很好的实现了模拟淘汰的操作。

缺点：学习新的程序知识。

4　数学推导法

模拟法效率很低，其时间复杂度为O（mn）。当n和m很大时，很难在短时间内得出结果。如果能得出一个通式，就可以利用递推来快速解决。下面给出推导的过程（假设从0到N-1）：

（1）第一个被删除的数为（m-1）%n。

（2）假设第二轮的开始数字为k，那么这n-1个数构成的约瑟夫环为k，k+1，k+2，k+3，.....，k-3，k-2。做一个简单的映射。

这是一个n-1个人的问题，如果能从n-1个人问题的解推出n个人问题的解，从而得到一个递推公式，那么问题就解决了。假如我们已经知道了n-1个人时，最后胜利者的编号为x，利用映射关系逆推，就可以得出n个人时，胜利者的编号为（x + k）%n。其中k等于m%n。代入（x + k） % n＜=＞（x + （m % n））%n ＜=＞ （x%n + （m%n）%n）%n ＜=＞ （x%n+m%n）%n ＜=＞（x+m）%n。

（3）第二个被删除的数为（m - 1） % （n - 1）。

（4）假设第三轮的开始数字为o，那么这n - 2个数构成的约瑟夫环为o，o+1，o+2，......o-3，o-2.。继续做映射。

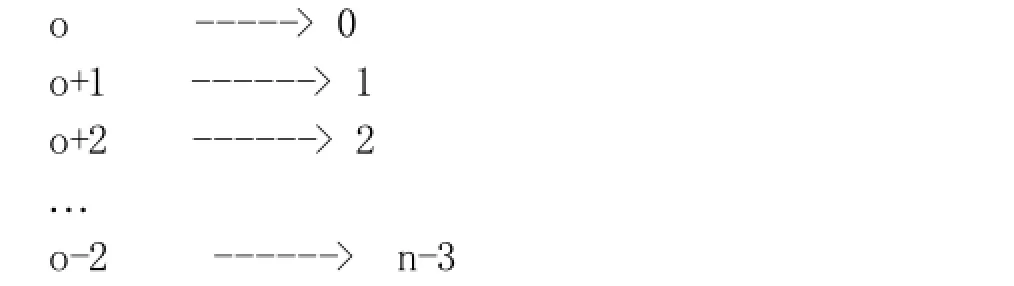
这是一个n-2个人的问题。假设最后的胜利者为y，那么n-1个人时，胜利者为（y+o）%（n-1），其中o等于m%（n-1）。代入可得（y+m）%（n-1）， 要得到n-1个人问题的解，只需得到n-2个人问题的解，倒推下去。只有一个人时，胜利者就是编号0。下面给出递推式：

f［1］=0；

f［ i ］=（ f ［i -1］ + m）%i； （i＞1）

有了这个公式，我们要做的就是从1-n顺序算出f的数值，最后结果是f［n］。因为实际生活中编号总是从1开始，我们输出f［n］+1，由于是逐级递推，甚至不需要保存每个f，程序也是异常简单：

Intans［10000］=｛0｝，i，n，m； //ans数组保存结果，还可用stl 中vector容器，甚至用一个变量代替。式进行计算

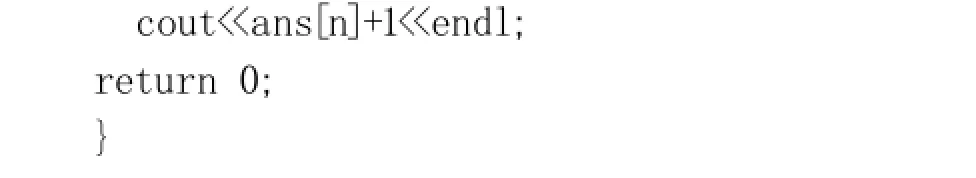
优点：运行速度快，代码简练。

缺点：数学推导过程要仔细推敲，慢慢消化理解。

对于猴子选大王这类环形问题，我们可以用不同的方法、不同的技术来解决，如何选择最优的设计方案呢，这就要我们在平时的学习中不断的积累知识，多思善想。适当地运用数学策略，不仅可以让编程变得简单，而且往往会成倍地提高算法执行效率。在此抛砖引玉，希望大家能提出更优、更易解决问题的方法。

Research on Simulation Program Design Method：Taking Choose Monkey King Program as an Example

Wang Sheng
（Qianwei Foreign Language Experimental School， Qianwei614400， China）

Abstract：Choose Monkey King is a classic programming problem, the article points out that can be done by different design methods: (1) the simulation method of array. (2) simulation list. (3) the stl list implementation. (4) mathematical deduction.

Key words：choose monkey king; simulation; list; stl list; mathematical deduction

作者简介：王胜（1975-），男，四川犍为。