间谍经纪人的最优侦查规模和决策阈值

杨伟松

(江西科技师范大学通信与电子学院， 南昌330013 )



间谍经纪人的最优侦查规模和决策阈值

杨伟松

(江西科技师范大学通信与电子学院， 南昌330013 )

摘要：为了考察争当少数者博弈模型中引入间谍经纪人后，间谍的侦查规模和决策阈值分布情况，考察了在不同比例间谍数目的情况下，间谍采取优胜劣汰的原则调整更换他们的侦查规模或决策阈值，发现当间谍数目较少时，间谍侦查规模取大数的数目比例居多；而当间谍数目较多时，间谍侦查规模取小数的比例居多。当侦查规模较小时，间谍倾向于取一半的决策阈值；而当侦查规模较大时，不同间谍的决策阈值分布比较广泛。

关键词：争当少数者博弈；间谍；侦查规模；决策阈值

0引言

D.Challet和Y.C.Zhang提出的争当少数者博弈模型[1-2]假设有N(奇数)个经纪人，在某时步必须选择A方或B方(如表示股票的买卖或开车选择道路A或道路B等)，当每个人独立地作出选择后，进入少数者方的人获胜(供大于求时,买方获利；供不应求时,卖方获利)。每个经纪人依据过去记录的公共信息作出决定。假定记录仅包含A方或B方是否为获胜方，而不告知实际的参与人数，这一系统的公共信息(即取胜方的记录)可以用二进制序列表示，当A方为获胜方时用”1”表示，否则用”0”表示。还进一步假定每个经纪人的记忆容量有限并且相同，只能记住最近m次的获胜方记录，并依赖他们作出当前时刻的决定。一个记忆容量为m的策略是在给定某种获胜方记录(m比特历史)下对下一时刻获胜方的预测。经纪人根据策略的预测选择去A方或B方，对给定m，有2m种不同的历史，22m种不同的策略。

博弈开始时,每人随机地从这22m个策略中抽出S个(允许相同)作为自己的策略。每过一时刻，每人对作出正确预测获胜方的策略加一虚分，否则扣一分。这样各人每次决策时，就依据这些策略的虚分，选择虚分最高者进行决策 (如有多个相同虚分最高策略，则从中任选一个进行决策)。经纪人共同享有的信息，即m位的二进制获胜方历史记录则去掉左边一位，而在右端加上一位当前时刻的获胜方记录。

自从争当少数者博弈模型提出以后，由于它揭示刻画了大量社会，经济，生态系统中的普遍现象，立即成为热门的研究课题，出现了大量的研究工作。我本人以前也对这个模型做过若干个研究工作[3-6]。例如，将模型中经纪人的二进制串策略看成不同历史条件下子策略的集合体，对子策略按成功率从大到小排序，替换成功率小的子策略，或者对表现好的策略按遗传算法产生子代策略用来替换表现差的策略，能够使模型系统功能和资源利用效率得到优化。

You-Yang Yu 等[7]设想在基本争当少数者博弈模型引入间谍经纪人，间谍经纪人不具有普通经纪人的对应于各种公共信息历史条件的二进制串策略，而是侦查一小组普通经纪人的决策，然后再采用该小组普通经纪人的少数方的决策。他们发现一定比例的间谍经纪人能够使正常经纪人的成功率变大。

本文考察了特定间谍经纪人数目比例条件下间谍的最优侦查规模和决策阈值。

1演化模型I

假设争当少数者博弈模型系统包含101个普通经纪人，采用模型的标准策略进行决策。然后假设在模型系统中加入间谍经纪人，间谍经纪人的数目分10，20，40，60四种情况。间谍经纪人的侦查规模，也就是侦查的范围所包含的普通经纪人的数目分少(11个)，中(51)，多(91)3个档次。

当间谍数目为10时，让模型系统演化1 000代，每代演化1 000时步。演化开始时普通经纪人的策略虚分和间谍的实分都置零，让每个间谍随机选择他的侦查规模，即在11，51，91三个数目的侦查数中任意选择一个作为他的侦查规模。每时刻间谍采纳他所侦查的人群中少数方的决策，每时刻统计所有普通经纪人和间谍经纪人的决策，总共人数少的一方为获胜方。普通经纪人给他的每个策略打虚分并根据虚分进行决策的机制同于争当少数者博弈基本模型。间谍经纪人根据侦查做出的决策如果和最后整个系统的获胜方相同，则该间谍加一实分；如果相反，则减一实分。每代结束时，实分最低的5个间谍将随机替换他的侦查规模。然后新一代开始时所有普通经纪人的策略虚分和间谍实分都重新置零。经过1 000代的演化后，间谍的侦查规模人数分布如图1，图1中横坐标1代表侦查规模为11，横坐标2代表侦查规模为51，横坐标3代表侦查规模为91。

当间谍数目为20时，假设每代结束时5个实分最低的间谍随机更换侦查规模，然后新一代开始时所有普通经纪人的策略虚分和间谍的实分都重新置零。经过5 000代演化后间谍的侦查规模人数分布如图2所示，从图1，图2可以发现当间谍数目比较少时，拥有最大侦查规模的间谍数目比例最大，这说明当间谍数目较少时，侦查规模越大或侦查范围越广，越对间谍的收益有利。

当间谍数目分别为40或60时，假设每代结束时10个实分最低的间谍随机更换侦查规模，然后新一代开始时所有普通经纪人的策略虚分和间谍的实分都重新置零。经过1 000代演化后间谍的侦查规模人数分布分别如图3和图4所示。

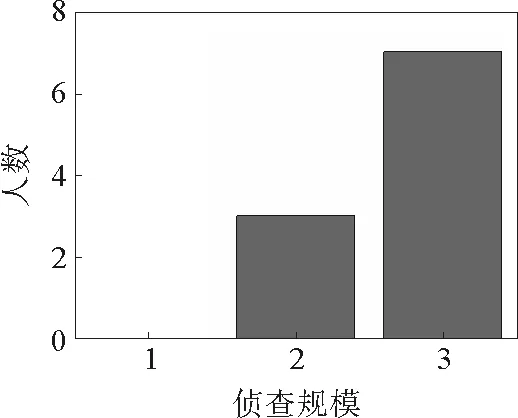
图1　间谍数目为10时经过演化后间谍的侦查规模人数分布

图2　间谍数目为20时经过演化后间谍的侦查规模人数分布

图3　间谍数目为40时经过演化后间谍的侦查规模人数分布

从图3，图4可以发现当间谍数目比较多时，拥有最小侦查规模的间谍数目比例最大，这说明当间谍数目较多时，侦查规模或侦查范围越小，越对间谍的收益有利。

2演化模型II

假设争当少数者博弈模型系统包含101个普通经纪人和40个间谍经纪人，间谍经纪人的侦查规模，仍然分少(11个)，中(51)，多(91)3个档次。原始间谍经纪人采用侦查范围少数方的决策，即小于侦查小组人数一半的那方的决策。我们假设间谍经纪人可以采用不同的决策阈值，即不一定采纳人数小于侦查小组人数一半的那方决策，而可能取其他的阈值。阈值比例p可以取10%,20%，…，90%,100%等10个数中的任一个，因而采用不同决策阈值的间谍也就分成了10个小组。某间谍侦查小组中若A方的人数小于侦查小组的总人数即侦查规模乘以阈值比例p，则该间谍就决定去A方，否则去B方。

假设模型系统每代演化1 000时步，第一代开始前让每个间谍随机选择他的决策阈值，并且普通经纪人的策略虚分和间谍的实分都置零。每时刻间谍决策的方式如上段所述。每代结束时，实分最低的10个间谍将随机替换他的决策阈值。然后新一代开始时所有普通经纪人的策略虚分和间谍的实分都重新置零。

当间谍的侦查规模为11时，让系统演化5 000代，演化后间谍的不同决策阈值人数分布如图5所示。

当间谍的侦查规模为51时，让系统演化1 000代，演化后间谍的不同决策阈值人数分布如图6所示。

图4　间谍数目为60时经过演化后间谍的侦查规模人数分布

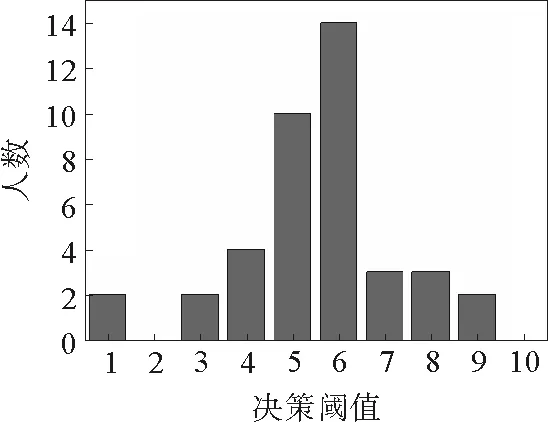
图5　间谍侦查规模为11时经过演化后间谍的决策阈值人数分布

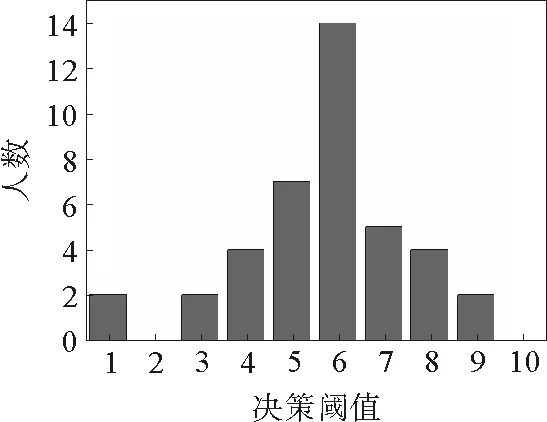
图6　间谍侦查规模为51时经过演化后间谍的决策阈值人数分布

当间谍的侦查规模为91时，让系统演化1 000代，演化后间谍的不同决策阈值人数分布如图7所示。

从数值模拟结果可以看出当间谍的侦查规模较小(11，51)时，间谍的决策阈值以中间值(0.5，0.6)居多，同普通情形类似。而当间谍的侦查规模较大(91)时，间谍的决策阈值分布则比较广泛，与普通情形不同。

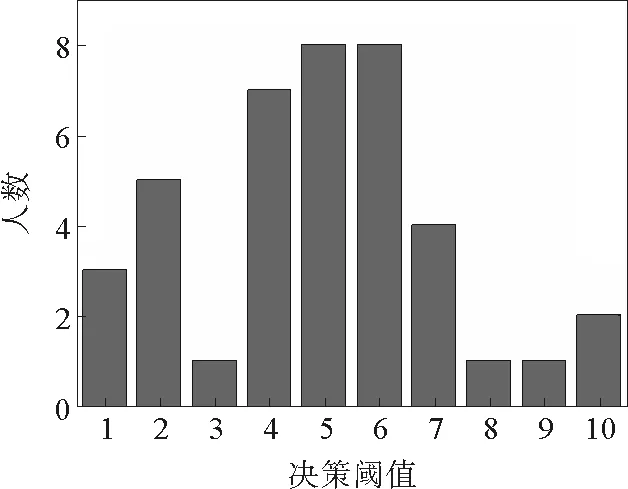
图7　间谍侦查规模为91时经过演化后间谍的决策阈值人数分布

3讨论

从演化模型I的数值模拟结果看，间谍与普通经纪人之间明显存在信息相互作用。当间谍数量较少时，间谍的侦查规模越大，越能给间谍带来有利的收益；而当间谍数量较多时,则变成侦查规模越小,越对间谍有利，这同我们的直觉推理是相符的。

当间谍数量较少时，模型系统每时刻的获胜方基本上就是普通经纪人人数少的那方，这时间谍侦查普通经纪人的范围越大，选择侦查小组中的少数方就越可能同该时刻系统的获胜方相符，从而越可能带来收益。而当间谍数量较多时，较多间谍都选择进入普通经纪人人数少的一方最后反而会使这方变成总人数多的一方，所以间谍侦查普通经纪人的范围越小反而越有利。

从演化模型II的数值模拟结果看，当间谍的侦查规模较小时，间谍倾向于普通情形，即选择侦查小组中普通经纪人数较少一方；而当间谍的侦查规模较大时，不同间谍的决策阈值则分布比较广泛。

我们认为，随着间谍侦查规模的增大，如果间谍仍然继续保持普通情形，选择侦查小组中普通经纪人人数少的一方，由于此时侦查小组中的普通经纪人数目已经接近整个系统的普通经纪人的总数目，因此大多数间谍会进入到普通经纪人人数较少的一方，结果最后反而使该方成为总人数较多的一方。所以在侦查规模很大的情况下，间谍的决策阈值趋向于广泛分布。

根据我们经过数值模拟计算的结果，可得出结论，当间谍数目比例较小时，侦查规模越大对间谍越有利；反之，当间谍数目比例较大时，则侦查规模越小越对间谍有利。对于第二种演化模型，间谍数量固定，当间谍的侦查规模较小时，间谍的决策阈值接近于普通情形；而当间谍的侦查规模较大时，间谍的决策阈值趋向于广泛分布。我们认为这些结果或结论对于包含间谍经纪人和普通经纪人的社会系统的控制和管理有一定的参考借鉴意义。

参考文献:

[1]Challet D, Zhang Y C. Emergence of cooperation and organization in an evolutionary game[J]. Physica A, 1997, 246(3/4): 407-418.

[2]Challet D, Zhang Y C. On the minority game: analytical and numerical studies[J]. Physica A, 1998, 256: 514-532.

[3]Yang W S, Wang B H, He P, et al, Sub-strategy updating evolution in minority game[J]. Chin Phys, 2003, 12: 931-935.

[4]Yang W S, Wang B H, Quan H J, et al. Strategy uniform crossover adaptation evolution in a minority game[J]. Chin Phys Lett, 2003, 20: 1659-1661.

[5]Yang W S, Wang B H, Wu Y L, et al. Searching good strategies in evolutionary minority game using variable length genetic algorithm[J]. Physica A, 2004, 339: 583-590.

[6]Yang W S, Li P，Zou S S, et al. Local minority game with evolutionary strategies[J]. China Phys Lett, 2006, 23: 1961-1964.

[7]Yu Y Y, Xu C, Gu G Q, et al. Spies in the minority game[J]. Phys Rev E, 2008, 77(1): 011106.

(责任编辑耿金花)

The Best Investigation Scope and Decision Threshold of Spy Brokers

YANG Weisong

(Jiang Xi Normal University of Science and Technology, Communication and electronic, Nanchang, 330013，China)

Abstract:In order to investigate the distribution pattern of investigation scope and decision threshold of spies when introduce spy agents into the minority game model, we investigate different situations with different spy number proportions. Spies take the principle "win stay, lose move" to adapt their investigation scope or decision threshold. It was found that when spy number is small, the proportion of large investigation scope is in the majority; yet when spy number is large, the proportion of small investigation scope is in the majority. When investigation scope is small, spy prefer to adopt half decision threshold; yet when investigation scope is large, the distribution scope of decision threshold of different spies is widespread.

Key words:minority game； spy； investigation scope； decision threshold

文章编号：16723813(2016)01010704;

DOI:10.13306/j.1672-3813.2016.01.012

收稿日期：2015-09-23

作者简介：杨伟松(1977-), 男, 江西南昌人，讲师，主要研究方向为经济物理、复杂性科学。

中图分类号：N93;N94;C935;C94

文献标识码：A