利用堆数据结构实现邻域重叠社团结构挖掘

任成磊, 韩定定, 蒲　鹏, 张嘉诚

(华东师范大学信息科学技术学院, 上海 200241)



利用堆数据结构实现邻域重叠社团结构挖掘

任成磊, 韩定定, 蒲鹏, 张嘉诚

(华东师范大学信息科学技术学院, 上海 200241)

摘要:基于当前复杂网络中社团划分算法普遍存在算法复杂度过高以及重叠节点挖掘不准确的局限性，提出了一种高效、快速、准确的社团划分算法。基于贪婪算法，建立最大模块度矩阵，并采用堆数据结构，划分非邻域重叠社团。通过分析局部网络的连边情况，计算邻域社团的划分密度，以准确挖掘社团间的重叠节点。新算法经过仿真分析和实证研究表明，算法复杂度降到近线性。

关键词：社团挖掘；邻域重叠；模块度；划分密度；时间复杂度

0引言

随着对网络性质的物理意义和数学特性的深入研究，人们发现在社会网、神经网、蛋白质网、万维网、通信网等网络中，普遍存在着一种特性——社团结构[1-4]。网络是由若干个团簇构成的，每个团簇内部的节点之间的连接非常紧密，但是各个团簇之间的连接却相对比较稀疏。这些子团簇就被称为社团，社团结构可以直观形象地揭示一个网络内部是如何自组织的，以及各个团簇之间的关系。因此，复杂网络社团结构的探测研究，对于网络的拓扑结构分析、功能的理解和网络行为动力学预测等有着重要的意义[5-6]。

近几年，复杂网络中社团结构的挖掘得到了各个领域科学家的广泛研究。Kernighan等[7]基于贪婪算法的基本原理，通过优化两个社团之间的连边，准确地将网络划分为两个已知大小的社团。Giran等[8]基于各个节点间的连接强度，提出了一种分裂方法，通过不断地从网络中移除介数最大的边，把网络自然地划分为不同的社团结构。Newman等[9]基于模块度，提出了一种快速凝聚算法，算法具有较低的复杂度，可以实现大规模网络社团结构的快速划分。Clauset等[10]在Newman快速算法的基础上，通过更新网络的模块度，提出了一种新的贪婪算法，该算法的复杂度只有O(nlog2n)，已接近线性，是目前在事先不知道社团数目的情况下，最快的社团划分算法。以上诸多算法可以将网络划分为若干个互相分离的社团，而现实中很多网络并不存在绝对的彼此独立的社团结构；相反，他们是由许多彼此重叠的社团构成。比如，我们每个人根据不同的分类方法都会属于多个不同的社团(如学校、家庭、不同的兴趣小组等)，因此以上的社团划分算法并不适合重叠社团结构的划分[11]。近几年，重叠社团结构的丰富性引起了众多学者的广泛研究，很多重叠社团结构挖掘算法被提出。Palla等[12]提出了一种派系过滤算法，通过挖掘网络中的全耦合子图，实现重叠社团结构划分。杨欢等[13]基于完全子图的社团探测算法，通过计算每一对完全子图的重叠节点个数，设置合并完全子图的阈值，快速地实现网络中重叠社团结构挖掘。Ahn等[14]通过对网络中的边进行社团划分，而不是传统方法中的节点，以划分密度D为重叠社团的检测标准，有效地实现了网络中重叠节点的挖掘。张忠元等[15]提出一种二元对称矩阵分解方法，首先利用非负对称矩阵算法对网络的社团成员矩阵初始化，然后对初始成员矩阵进行优化，最后统计各个社团中的连边数以及节点数并计算整个网络的划分密度，从而准确地挖掘出社团间的重叠部分。邻域重叠社团划分算法虽然可以准确地挖掘网络中的重叠节点，但是在网络社团结构的划分上却存在模糊性，社团划分不够准确，此外算法复杂度较高，难以实现大规模网络重叠节点挖掘。针对上述问题，本文将二者的优势揉合到一起，利用堆的数据结构，快速地实现非邻域社团结构划分，并通过分析局部网络的连边情况，利用划分密度准确地挖掘出网络中的重叠节点。

1模块度Q和划分密度D

为了衡量网络社团划分结果的合理性，科学家提出了一系列衡量标准。其中，在非邻域社团结构划分方面，Newman等[8]引进了一个衡量网络划分质量的标准——模块度Q。Q值表征了网络社团划分的质量，Q值越大，表明社团内部的连边越多，而社团之间的连边越少，此时社团划分质量也越高。模块度值Q的公式为

(1)

其中，m为网络中的边数，vw为节点，Avw为网络的连接矩阵中的元素，若节点v和节点w之间有边相连接则值为1，否则为0，kv表示节点v的度值，kw表示节点w的度值，若节点v和节点w属于一个社团，则δ(cv，cw)函数值为1，否则为0。式(1)的物理意义是：网络中连接两个同种类型的节点的边(即社团内部边)的比例，减去在同样的社团结构下任意连接这两个节点的边的比例的期望值。如果社团内部边的比例不大于任意连接时的期望值，则有Q=0。Q的上限值是1，Q越接近这个值，就说明社团结构越明显。实际网络中，该值通常位于0.3～0.7之间。在以往的非邻域重叠社团划分研究工作中，模块度Q被作为一个重要的衡量标准，用以衡量社团划分结果的准确性。

随着复杂网络社团挖掘研究的深入，人们发现复杂网络中很多社团之间都存在着邻域重叠结构。因为传统的社团划分算法难以实现邻域重叠结构划分，所以许多针对网络邻域重叠社团结构的挖掘算法被提出。传统的模块度Q已经难以准确衡量邻域重叠社团划分算法的准确性，Ahn等[14]基于局部网络的连边情况，提出了一个衡量网络邻域社团划分质量的标准——划分密度D。在一个有M条边，N个节点的网络中，社团c的划分密度为

(2)

其中，Dc为社团c的划分密度，mc为社团c中的边数，nc为社团c中的节点数。整个网络的划分密度是所有子社团密度值之和的平均值，对应的公式为

(3)

2基于堆数据结构的社团挖掘

堆数据结构是一种数组对象，可以被认为是一棵完全二叉树。根据完全二叉树中节点的优先级可以将堆分为最大堆和最小堆两种类型。最大堆中父节点的值大于两个子节点的值，而最小堆中父节点的值小于两个子节点的值。图1是最大堆与最小堆的一个例子。

图1　最大堆与最小堆示例图

由于堆具有独特的数据结构，常被用于实现数据排序，算法简单，复杂度低。在本文中，首先采用最大堆数据排序法来计算和更新网络的模块度，快速地实现网络的非邻域社团结构划分，并以此作为初始的社团成员矩阵；然后，再对网络中的边进行分析，若一条边中的两个节点在两个不同的社团中，那么这两个节点中有一个节点应该是邻域社团的重叠节点，结合当前合理的邻域重叠社团衡量标准——划分密度D，分析该对节点中哪一个节点算作重叠节点更加合理。

在本文中，邻域重叠社团结构挖掘算法一共用到了3种数据结构：

1)模块度增量矩阵ΔQij：它与网络的邻接矩阵A一样，是一个稀疏矩阵，初始化公式如下所示：

(4)

其中，m为网络中的总边数，ki为节点i的度，kj为节点j的度。

2)最大堆H。最大堆H中存储的是模块度增量矩阵ΔQij每一行的最大元素，以及最大元素对应的两个社团的编号i和j。

3)辅助向量α1：辅助向量初始化公式为

(5)

其中，m为网络中的总边数，ki为节点i的度。

基于以上3种数据结构，邻域重叠社团挖掘算法流程为

1)初始化。利用公式(4)、(5)计算网络初始化模块度增量矩阵ΔQij和辅助向量i，得到了初始化的模块度增量矩阵以后，利用最大堆排序法，读取增量矩阵中的每一行最大元素ΔQij构成最大堆H。

2)从最大堆H中选择最大的ΔQij，合并相应的社团i和社团j，标记合并后的社团序号为j；并更新模块度增量矩阵ΔQij、最大堆H和辅助向量αi，以及合并之后的模块度值Q+ΔQij。

(1)ΔQij的更新：删除第i行和第i列的元素，更新第j行和第j列的元素：

(6)

(2)H的更新：每次更新ΔQij后，更新最大堆中相应行的最大元素。

(3)αi的更新：

(7)

3)重复步骤2)，直到最大堆H中的元素全部变成负值，此时得到的就是网络最佳的非邻域重叠社团结构。

4)读取网络连边Lsd，若当前边对应的两个节点从属于不同的社团，分别将源节点(s)和目标节点(d)作为重叠节点，重新统计各个社团中的连边数和节点数，利用划分密度公式计算得到源节点的划分密度DS和目标节点的划分密度Dd。若DS大于Dd，则源节点是两个社团间的重叠节点，反之目标节点是两个社团间的重叠节点，记录重叠节点。

5)重复步骤4)，直到网络中的所有边都被检测完毕，将非邻域重叠社团成员矩阵和重叠节点结合，实现网络的邻域重叠社团结构挖掘。

3算法复杂度近线性

本文提出的邻域重叠社团结构挖掘算法主要是由两部分组成：非邻域重叠社团结构划分和社团间重叠节点挖掘。本文基于堆数据结构快速实现社团成员矩阵的初始化，对于一个有n个节点，m条边的网络，算法复杂度为O(mdlogn)(d表示网络的深度)[9]。而现实中很多网络都是稀疏网络，则有m≈n、d≈logn，在这种情况下，非邻域重叠社团划分算法的复杂度近似为O(nlog2n)。此时算法复杂度近似为线性，运行速度快。此外，算法本身基于模块度值，通过更新模块度增量矩阵得到整个网络的最大模块度值，所以最终的社团划分结果也是最佳结果。在最优的非邻域社团结构基础上，遍历网络中的m条边，分析网络中的连边信息。若当前边上的一对节点从属于不同的社团，则需要把其中的源节点和目标节点分别作为重叠节点，统计对应的社团中新出现的边，并计算网络的划分密度D，其中较大值对应的节点即为重叠节点。将网络信息以邻接表的形式存储，当社团中增加一个节点，判断该节点的邻居节点是否也在当前社团中，此时整个过程的算法复杂度为O(k)(其中k为网络的平均度)。假设在最坏的情况下，每条边对应的节点对都从属于不同的社团，则社团重叠结构挖掘过程的算法复杂度为O(mk)，在稀疏网络中m≈n，此时算法的复杂度近似为O(nk)。综上所述，本文提出的邻域重叠社团结构挖掘算法的复杂度近似为O(n(log2n+k))，近似为线性，因此可以将它应用到大规模网络邻域重叠社团结构挖掘。

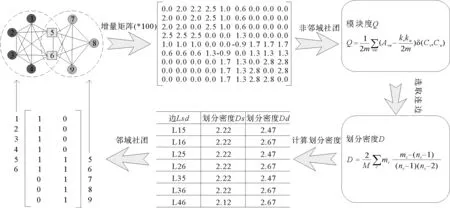
图2　模拟网络验证邻域重叠社团结构挖掘算法的有效性

4实验结果与分析

4.1利用模拟网络验证算法

本文利用一个模拟网络来验证算法的准确性，在图2中，一个模拟网络中有两个社团，其中节点5和节点6是两个社团所共有的重叠节点。首先，我们对网络进行初始化，计算得到模块度增量矩阵ΔQij和辅助向量αi以及最大堆H；然后利用堆的数据结构计算和更新网络的模块度，快速地实现非邻域社团结构划分；最后遍历网络中的所有边，基于划分密度D挖掘出社团之间的重叠节点，并将重叠节点与非邻域社团结构相结合，得到邻域重叠社团结构。从图2中可以看到，邻域重叠社团挖掘算法准确地将网络划分成两个重叠的社团，其中1表示该节点属于社团，0表示不属于社团。

4.2实证网络验证算法

在本节，我们将本文所提出的邻域重叠社团结构划分算法应用到已知社团结构的空手道俱乐部网和海豚网中，实现网络中的邻域社团结构挖掘，以验证邻域社团划分算法的准确性。

20世纪70年代，Zachary[16]基于美国一所大学中的空手道俱乐部成员间的相互社会关系，构造了他们之间的关系网。在他研究过程中，该俱乐部的主管与校长之间因是否提高俱乐部收费的问题产生了争执，导致俱乐部分裂成了两个分别以主管和校长为核心的小俱乐部。因此空手道俱乐部网成为复杂网络社团划分方面的一个经典网络，被广泛用于检验社团划分算法的准确度。图3为利用本文所提出的邻域重叠社团结构划分算法对经典的空手道俱乐部网络进行邻域社团划分所得结果。

其中，橙色节点和淡粉色节点分别属于不同的社团，中间的紫色节点是两个社团之间的重叠节点。基于模块度Q，利用堆数据结构合理地将空手道网络划分为彼此不重叠的两部分，其社团结构与现实中的空手道俱乐部网络几乎一致。通过分析网络中的连边情况，利用划分密度D，准确地挖掘出网络中的重叠节点，其中节点1,3,9,34不但与左边社团中多个节点相连，而且还与右边多个节点之间有联系，因此应该是两个社团之间的共有部分。而节点31虽然只与左边社团中的一个节点相连，但是起到了桥梁作用，两个社团可以通过节点31进行交流，所以节点31也应该是两个社团之间的重叠节点。

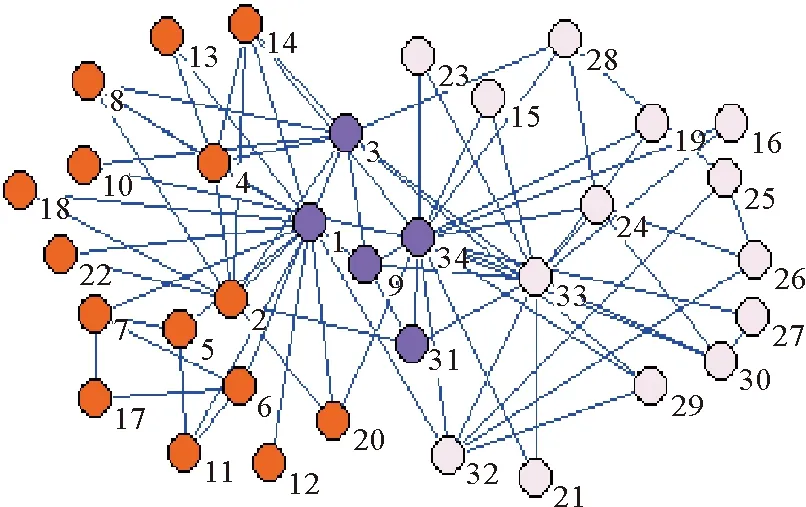
图3　空手道俱乐部重叠社团划分结果

图4　海豚网重叠社团划分结果

Lusseau等[17]对生活在新西兰神奇海湾中的一群海豚做了跟踪调查，发现它们之间同样存在着社团结构。图4是利用本文所提出的邻域重叠社团结构划分算法对海豚网络进行邻域社团划分所得结果。红色节点和绿色节点分别属于不同的社团，中间的蓝色节点是两个社团之间的重叠节点。节点2,29,31不但与左边社团中多个节点相连，而且还与右边多个节点之间存在关系，因此也应该是两个社团之间的共有部分。节点8,58虽然只与右边社团中的一个节点相连，但是这两个节点同样也起到了桥梁作用，使得左右两个社团可以通过节点8,58进行交流，所以节点8,58也应该是两个社团之间的重叠节点。

在空手道俱乐部网和海豚网中，利用本文提出的邻域重叠社团结构划分算法，得到的社团结构与实际情况相一致，进一步证实了算法的准确性。此外，本文还将邻域重叠社团结构划分算法运用到科学家合作网中[8]。图5是对科学家合作网进行邻域社团划分所得结果。

图5　科学家合作网重叠社团划分结果

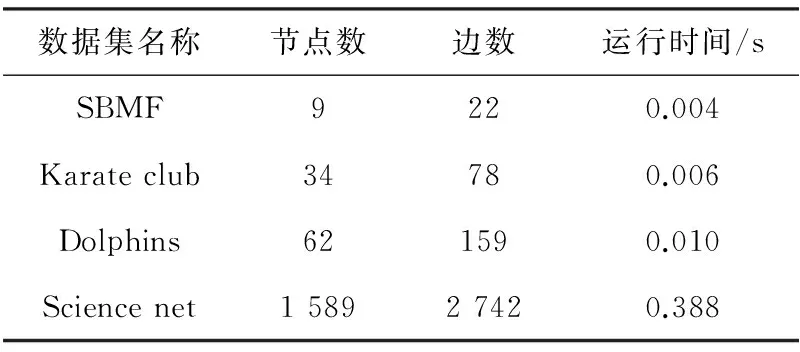
数据集名称节点数边数运行时间/sSBMF9220.004Karateclub34780.006Dolphins621590.010Sciencenet158927420.388

在图5中，科学家合作网中的最大连通网被划分成8个社团，不同颜色的团簇代表了一个社团结构，社团之间的红色的节点表示的是重叠节点。从图5可以看出，社团内部的节点之间联系非常紧密，而社团之间的连接却相对比较稀疏。社团间的重叠节点大多是度值比较大的节点或者是与度值较大的重叠节点关系紧密的小度值节点。图5中的网络拓扑结构合理地反映了科学家之间的合作模式：相同研究方向的科学家之间的合作非常紧密，具有明显的聚簇现象；同时不同研究方向的科学家之间也存在着学术交流，但这往往发生在学科代表的身上以及他的研究团队中。比如，在复杂网络领域，Mark Newman是一名伟大的物理学教授，其团队主要从事网络拓扑结构和网络功能的研究。由于Newman团队取得的成绩非常突出，导致很多领域的科学家都会与他的团队进行合作，此时他的团队就成为不同研究领域的社团之间的重叠节点。在图5中，Newman及其团队对应的是蓝色社团中的度值较大的红色节点以及度值较小的红色节点。

由于本文采用了堆数据结构，从计算科学的角度优化了社团结构的划分，极大程度上降低了算法复杂度，加快了社团结构的划分，表1是程序在不同的数据集中的运行时间。

从表1可以看到，本文所提出的社团划分算法可以快速地实现邻域社团结构划分，当网络规模增大时，程序耗时仍然较低。因为本文所提出的社团划分算法的算法复杂度近似线性，所以其适用于大规模复杂网络，可以快速实现网络的邻域社团结构挖掘。

5结语

本文提出了一种复杂度近似线性的邻域重叠社团结构划分算法，可以准确、快速地实现网络社团划分以及重叠节点挖掘。基于模块度Q，本文采用堆的数据结构，快速地实现了非邻域社团划分，利用得到的非邻域社团构造初始社团矩阵，逐一分析网络中的连边，结合划分密度D，准确地实现了社团间重叠节点的挖掘。最后，本文利用模拟网络和经典的实证网络进一步证实了算法的高效性、准确性。

参考文献:

[1]Girvan M, Newman M E J. Community structure in social and biological networks[J]. Proceedings of the National Academy of Sciences, 2002, 99(12): 7821-7826.

[2]Adamic L A, Adar E. Friends and neighbors on the web[J]. Social Networks, 2003, 25(3): 211-230.

[3]Holme P, Huss M, Jeong H. Subnetwork hierarchies of biochemical pathways[J]. Bioinformatics, 2003, 19(4): 532-538.

[4]Newman M E J. The structure and function of complex networks[J]. SIAM Review, 2003, 45(2): 167-256.

[5]Guimera R, Amaral L A N. Functional cartography of complex metabolic networks[J]. Nature, 2005, 433(7028): 895-900.

[6]Flake G W, Lawrence S, Giles C L, et al. Self-organization and identification of web communities[J]. Computer, 2002, 35(3): 66-70.

[7]Kernighan B W, Lin S. An efficient heuristic procedure for partitioning graphs[J]. Bell System Technical Journal, 1970, 49(2): 291-307.

[8]Newman M E J, Girvan M. Finding and evaluating community structure in networks[J]. Physical Review E, 2004, 69(2): 026113.

[9]Clauset A, Newman M E J, Moore C. Finding community structure in very large networks[J]. Physical Review E, 2004, 70(6): 066111.

[10] Newman M E J. Finding community structure in networks using the eigenvectors of matrices[J]. Physical Review E, 2006, 74(3): 036104.

[11] Zhang X S, Li Z, Wang R S, et al. A combinatorial model and algorithm for globally searching community structure in complex networks[J]. Journal of Combinatorial Optimization, 2012, 23(4): 425-442.

[12] Palla G, Derényi I, Farkas I, et al. Uncovering the overlapping community structure of complex networks in nature and society[J]. Nature, 2005, 435(7043): 814-818.

[13] 杨欢，韩定定. 完全子图的邻域重叠社团结构探测[J]. 现代电子技术, 2012, 35(18):122-126.

Yang H, Han D D. Improvement of neighbourhood overlapping community detection algorithm based on complete subgraph[J]. Modern Electronics Technique, 2012, 35(18):122-126.

[14] Ahn Y Y, Bagrow J P, Lehmann S. Link communities reveal multiscale complexity in networks, 2010[J]. Nature, 466: 761.

[15] Zhang Z Y, Wang Y, Ahn Y Y. Overlapping community detection in complex networks using symmetric binary matrix factorization[J]. Physical Review E, 2013, 87(6): 062803.

[16] Zachary W W. An information flow model for conflict and fission in small groups[J]. Journal of Anthropological Research, 1977: 452-473.

[17] Lusseau D, Schneider K, Boisseau O J, et al. The bottlenose dolphin community of doubtful sound features a large proportion of long-lasting associations[J]. Behavioral Ecology and Sociobiology, 2003, 54(4): 396-405.

(责任编辑李进)

Finding Overlapping Community in Network by Using Modularity and Partition Density

REN Chenglei, HAN Dingding, PU Peng, ZHANG Jiacheng

(School of Information Science and Technology, East China Normal University, Shanghai 200241, China)

Abstract：The algorithms of detecting community in complex networks now have lots of disadvantages such as high complexity and ignorance of accurate overlapping nodes. This paper proposes a highly efficient, rapid and accurate community detection algorithm. Based on greedy algorithm, the community is divided by establishing the modularity matrix and adopting the data structure. Considering the edges between local communities, the overlapping community structure is accurately dug by computing the partition density. We evaluate our methods using both synthetic benchmarks and real-world networks, demonstrating the effectiveness of our approach. Our method runs in essentially linear time.

Key words：community mining; overlapping community; modularity; partition density; time complexity

文章编号：16723813(2016)01010206;

DOI:10.13306/j.1672-3813.2016.01.011

收稿日期：2015-07-09

作者简介：任成磊(1990-)，男，山东烟台人，硕士研究生，主要研究方向为智能计算、复杂网络。

中图分类号：TP393.02

文献标识码：A