基于有限单元法的重力梯度张量正演计算与分析

彭江英，吴　兴，韩文文，柳康伟

(成都理工大学 a.地球物理学院,b.信息科学与技术学院,成都　610059)



基于有限单元法的重力梯度张量正演计算与分析

彭江英a，吴兴a，韩文文b，柳康伟a

(成都理工大学 a.地球物理学院,b.信息科学与技术学院,成都610059)

摘要：由于重力梯度张量测量相对于重力异常测量有许多优点，因此对重力梯度的研究十分必要。在重力梯度各张量的正演计算中，复杂地质体的计算式难以直接推导，而利用有限元技术在复杂形体体积积分的优势，可以较为快速和简便地进行复杂模型的重力梯度全张量正演计算。通过模型的建立和正演计算，分析了球体模型梯度张量异常的平面和剖面特征，以及重力梯度张量与球体模型位置的规律；最后进一步利用复杂模型的重力梯度正演模拟，说明了重力梯度识别地下地质体位置的优势和不足。

关键词：重力梯度全张量；有限单元法；正演计算；异常识别

0前言

重力资料是区域地质研究的基础，不仅对于解析区域大地构造格架、板块运动、形成与演化等大尺度的基础性研究有参考价值，而且对于断裂分布、盆地划分、沉积厚度等重要油气地质问题也有相当程度的指导意义。地球重力场可用重力位(重力标量)、重力位梯度(重力矢量)和位的高阶导数来表示，重力矢量各分量的梯度是重力位的二阶导数[1]。重力梯度研究和测量开始于19世纪七十年代，重力梯度张量包含了对于大地测量和地球物理学中许多问题都十分重要的局部重力场信息[2]，它被广泛应用于大地测量学[3]、地球物理学、地质学、地震学[4]、海洋学[5]、航空和空间科学[3,5-7]等领域。与传统的重力异常测量相比，重力梯度张量测量有更高的灵敏度、短波信息丰富，包含多个信息不同的重力梯度张量分量，对惯性加速度不敏感等。

由于重力梯度测量相对于重力异常测量有上述各种优越性，对重力梯度的研究显得十分重要和必要的。重力梯度张量测量在国外已经十分成熟并进入了商业应用阶段，而在国内还处于起步阶段，但重力梯度张量处理和解释已经得到了开展。除了用重力梯度仪直接观测重力梯度张量，还可由重力异常数据经过一定的算法求得重力梯度张量，更直接的办法是直接用模型正演来计算简单模型研究复杂地质体。国内、外学者已经研究和提出了众多重力梯度的求取算法，例如样条函数插值法[8]、差商方法[9]、频率域中的傅里叶变换法[10]和余弦变换法[11]以及有限单元方法[12]等。作者介绍了重力梯度张量概念，利用有限元技术推导出梯度张量的计算式，计算并分析了球体模型张度张量异常的平面和剖面特征，总结了重力张量与球体模型位置关系的规律，最后进一步建立复杂模型，通过计算与分析认识到重力梯度在识别地下地质体位置的优势。

1重力梯度张量计算

1.1重力梯度张量概念

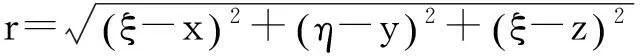
(1)

式中，G为万有引力常数。若对引力位U求一阶导数，则可得到重力三分量，如式(2)所示。

(2)

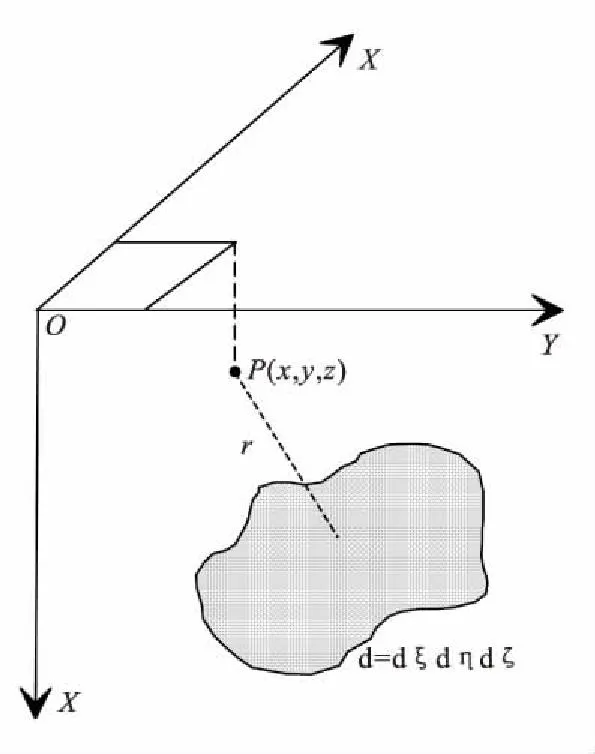
图1　笛卡儿坐标系下地质体空间位置示意图Fig.1　Spatial location of geological body in Cartesian coordinates

由于重力方向就是Z轴方向，所以所谓的重力异常就是引力位在Z方向的一阶导数，如式(3)所示。

(3)

而对引力位U求二阶导数，则重力梯度九分量(又称重力梯度全张量)可表示为式(4)。

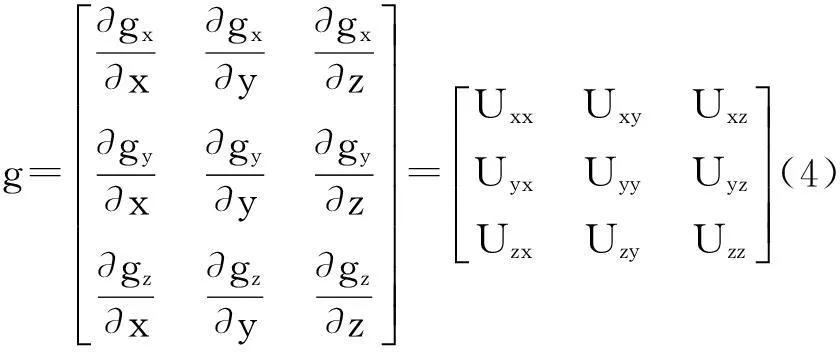
由于计算点在地质体外部，g满足自由空间的微分方程，见式(5)。

▽·g=0,▽×g=0

(5)

将式(2)代入式(5)，可以得到重力梯度各分量之间的关系如式(6)所示。

(6)

由式(6)可知，重力梯度全张量中只有5个独立的分量(由此可推导出其余分量)，见式(7)。

(Uyx,Uxz)=(Uzx,Uyz)=Uzy

(7)

将式(1)代入式(4)，可推导出重力梯度全张量的表达式[14]如式(8)所示。

(8)

1.2重力梯度张量的有限元计算

在正演计算中，一些简单规则的模型体(如球体、垂直棱柱体等)引起的重力梯度计算式可以由式(8)推算出来并直接计算；而对于复杂的组合模型或实际地质体来说，不容易推算出其计算式，可以用简单模型去叠加模拟逼近或将其简单化后再计算。采用有限单元法就可以将地下复杂的地质体划分为由有限多个有限大小的单元体组成的离散结构(或称有限网格)，有限单元之间相交的点称为结点。然后利用每一个单元求解在计算点产生的重力梯度异常值，最后进行叠加计算就可求得地下复杂地质体在观测平面的重力梯度异常。

为了采用有限单元离散复杂地质体，对于空间问题，常用的单元有四面体单元、长方体单元、任意六面体单元等，其中，四面体单元是最早被提出的最简单的空间单元，如图10所示，S(x,y,z)为单元内任意一点，S点与4个结点的连线把原四面体分割为4个小四面体，用V、V1、V2、V3、V4分别表示四面体1234、S234、S341、S412、S123的体积，令

(9)

(10)

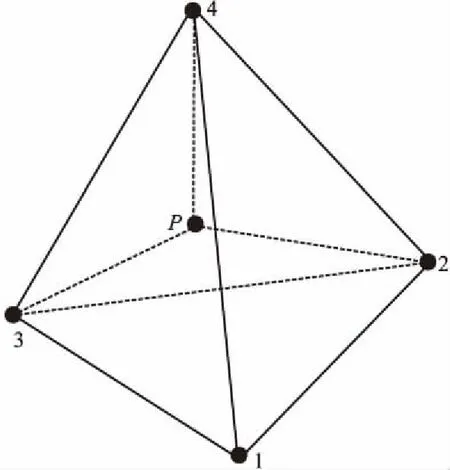
图2　四面体有限单元示意图Fig.2　Sketch map of tetrahedron elemnt

由于V=V1+V〗2+V3+V4，有

L1+L2+L3+L4=1

(11)

在四面体单元中，采用的是体积坐标(L1,L2,L3)，其Hammer积分形式[15]如式(12)所示。

F(b,b,a,b)+F(b,b,b,a)]

(12)

式中，权系数和积分点坐标关系[15]如表1所示。

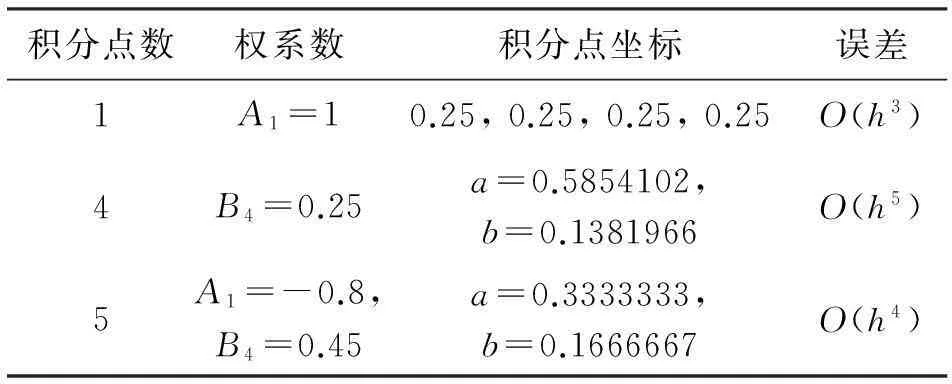
表1　Hammer积分的权系数和积分点坐标关系Tab.1　Weights and integration point coordinates of Hammer integral

将式(8)从直角坐标系转换到体积坐标系，见式(13)。

(13)

式中，|J|为坐标映射的雅可比行列式[15]，见式(14)。

(14)

由上述计算式可推算出线性四面体网格的重力梯度全张量表达式[12]，见式(15)。

2模型正演及分析

对较为常见的典型三度体(球体、水平圆柱体和棱柱体等)进行正演模拟计算，得出重力梯度张量异常曲线，并分析模型的重力梯度张量各个分量的曲线特征，同时分析所建立模型的不同体积元参数(如板状体的上顶边埋深及板状体厚度、倾角、球体的半径及球心的埋深、水平圆柱体的截面半径、中轴线埋深、水平延伸长度、棱柱体的各边长及顶界面埋深等)，对重力梯度张量异常曲线的响应特征及变化规律。

2.1单个球体模型

对球体模型重力梯度张量进行讨论时，设球体半径为r，球心埋深为h，剩余密度值均取为1 g/cm3。对不同球体半径及不同球心埋深所确定的模型进行正演计算，并对其重力梯度张量异常的特征进行对比分析。对于不同埋深、不同大小的球体模型，其重力梯度张量(Uxx、Uyy、Uzz、Uxy、Uxz和Uyz)等值线如图3—图5所示，图3—图5中黑色虚线为零值线，红色虚线表示球体在水平面上的投影。

从重力梯度张量异常图形可以归纳其各自的特点，由于目标体的模型具有对称性，其重力梯度张量的各分量等值线也具有对称性，既分别关于X、Y轴对称，也关于中心原点对称。梯度张量Uxx和Uyy分量等值线上有三个极值点，其中球心在水平面投影点(记为“O点”)处为极小值，等值线呈类椭圆形状向外扩散，越靠近O点等值线变得越密，呈现出明显的梯级带；轴线方向上远离O点异常值逐渐变大，并出现两个形态大小对称的异常极大值；零等值线呈靠近O点弯曲的形态。梯度张量Uxy分量平面等值线形态为“四叶草”形，等值线零值在X、Y轴上，曲线在靠近X、Y轴时出现明显的梯级带，梯度张量等值线有四个极值点，在1、3象限取得异常极大值，在2、4象限取得异常极小值，在极值点沿半径延长线像远离原点方向上，呈发散的形态，且等值线变稀疏。梯度张量Uxz和Uyz分量等值线形态成“扇贝”形，等值线零值在X轴或Y轴上，平面等值线有一正一负两个极值，从两个极值点靠近轴线的等值线变密，呈现明显的异常梯级带，远离O点方向，等值线变稀疏，呈波纹扩散形态。梯度张量Uzz为以O点为中心的一系列同心圆，在O点处取得极大值，零等值线范围大于球体在水平面投影的边界，从外侧到O点张量等值线先变密，在球体投影边界附近呈现明显的梯级带，继续向O心靠近等值线开始变稀疏。

图3　球体重力梯度张量等值线图(r=150 m，h=300 m)Fig.3　Contour map of gravity gradient tensors base on sphere(r=150 m,h=300 m)(a)Uxx;(b)Uyy;(c)Uzz;(d)Uxy;(e)Uxz;(f)Uyz

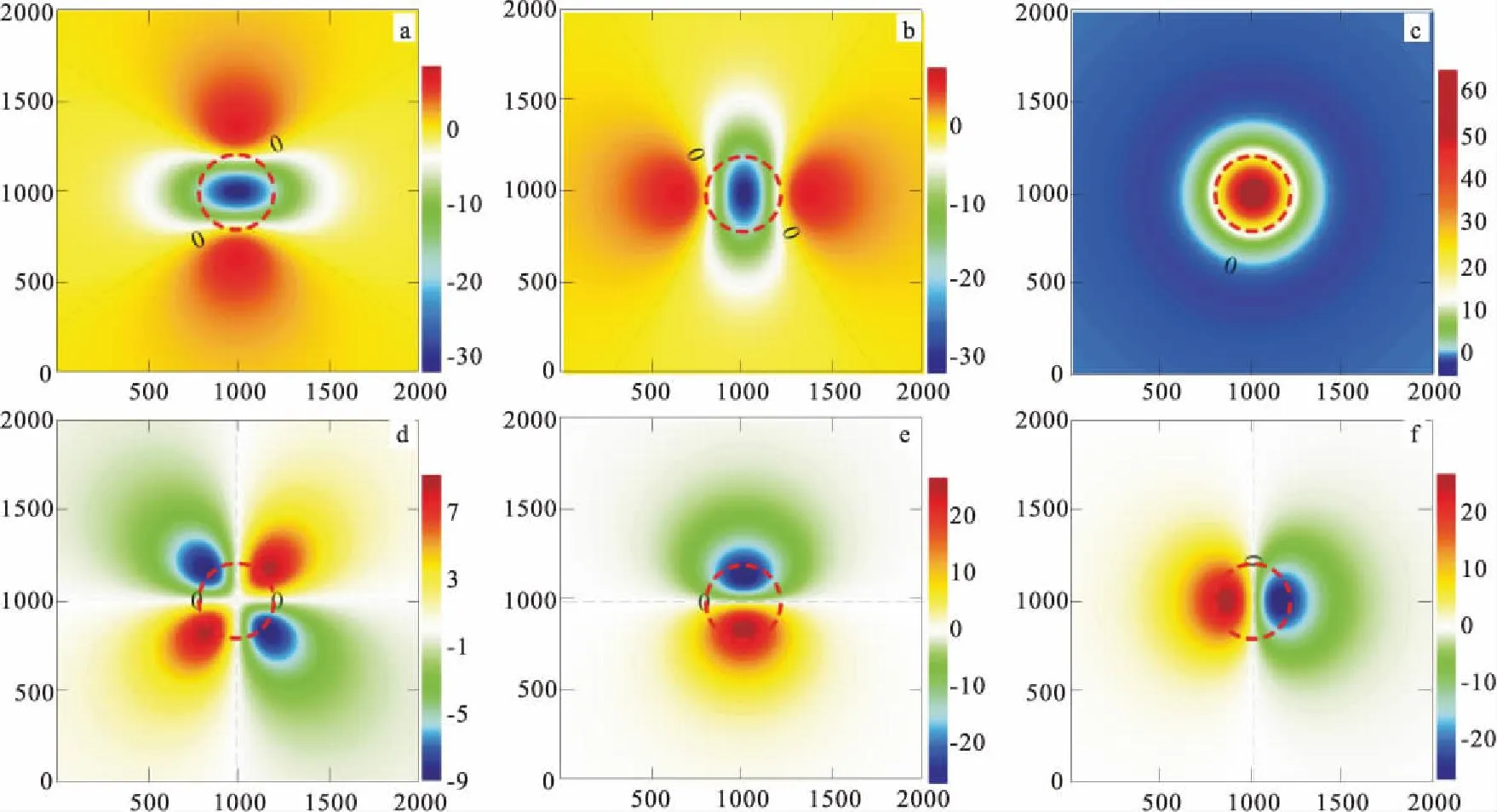
图4　球体重力梯度张量等值线图(r=200 m，h=300 m)Fig.4　Contour map of gravity gradient tensors base on sphere(r=20 m,h=300 m)(a)Uxx;(b)Uyy;(c)Uzz;(d)Uxy;(e)Uxz;(f)Uyz

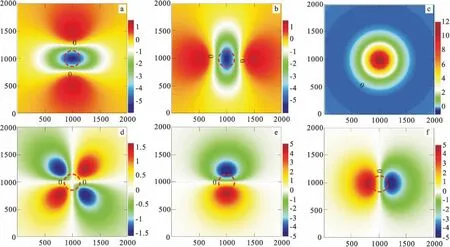
图5　球体重力梯度张量等值线图(r=150 m，h=400 m)Fig.5　Contour map of gravity gradient tensors base on sphere(r=150 m,h=400 m)(a)Uxx;(b)Uyy;(c)Uzz;(d)Uxy;(e)Uxz;(f)Uyz

为了分析梯度张量的各个分量等值线与球体埋深和半径的关系，选取不同的模型进行实验，并以零值线和极值点为参照进行分析。图3和图4显示了球心埋深相同、球体半径不同时重力梯度张量的等值线特征，对比各个分量曲线可以发现：当球体半径改变时，等值线的零值线和极值点的位置不变，只有异常幅度(极值点的大小)随着半径增大而增大。图3和图5显示了球体半径相同、球心埋深不同时重力梯度张量的等值线特征，对比各个分量曲线可以发现：当球心埋深增大时，除了异常幅度减小外，各个分量(除Uzz外)的极值点间距随之增大，而Uxx、Uyy和Uzz分量的零值线在主剖面(过O点的剖面)上间距也在增大。通过上述分析，说明了球体模型的重力梯度等值线对反映球体的埋深十分灵敏，而对球体的规模大小(半径大小)的反映却不太明显。

2.2复杂组合模型

为了模拟实际地质情况，反映重力梯度全张量在识别地下复杂地质体位置的可靠性，设计了一个组合复杂模型，该模型由多个不同埋深、不同大小和不同密度的垂直棱柱体组成，模型具体参数见表2，图8(a)和图8(b)分别显示了组合模型位置在XOY平面和YOZ平面的投影。图8(c)为组合模型的重力异常图，从图8中可以看到，模型A1和A2形成了独立的封闭异常，且异常范围和幅度较大，很容易辨别；叠加的模型B1和B2受到模型A1和A2的影响只是引起了等值线小幅度的向内弯曲，不能形成封闭曲线，很难分辨出这两个模型的存在；模型B3由于距离模型A1和A2较远，能够形成封闭曲线，较易识别；而模型C1、C2和C3由于规模较小，在模型A1和A2的影响下，在等值线上呈现小范围的异常凸点，不易识别。

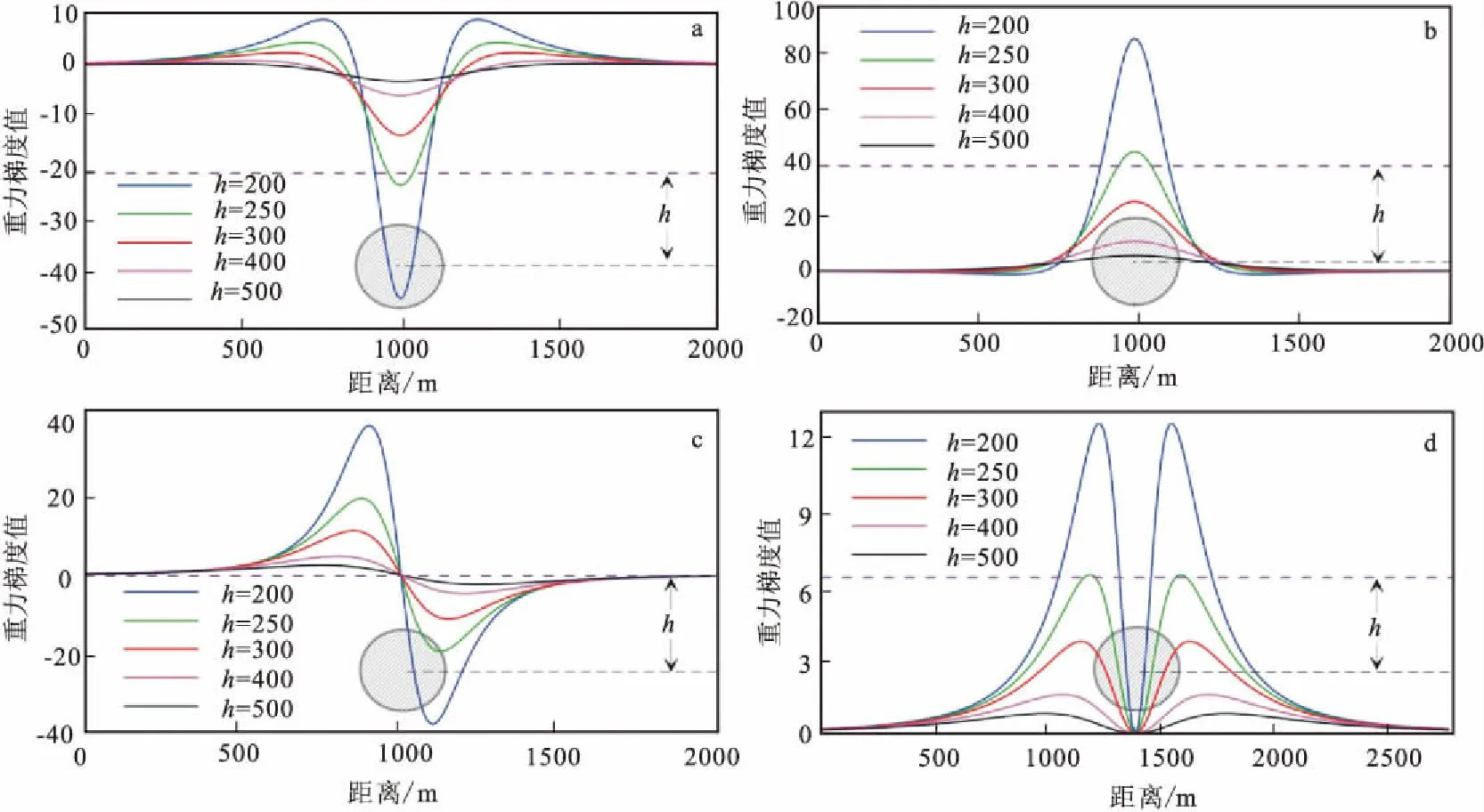
图6　不同埋深的梯度张量主剖面曲线Fig.6　Main sections of gravity gradient tensors base on different buried depth(a)Uxx(Uyy)；(b)Uzz；(c)Uxz(Uyz)；(d)Uxy

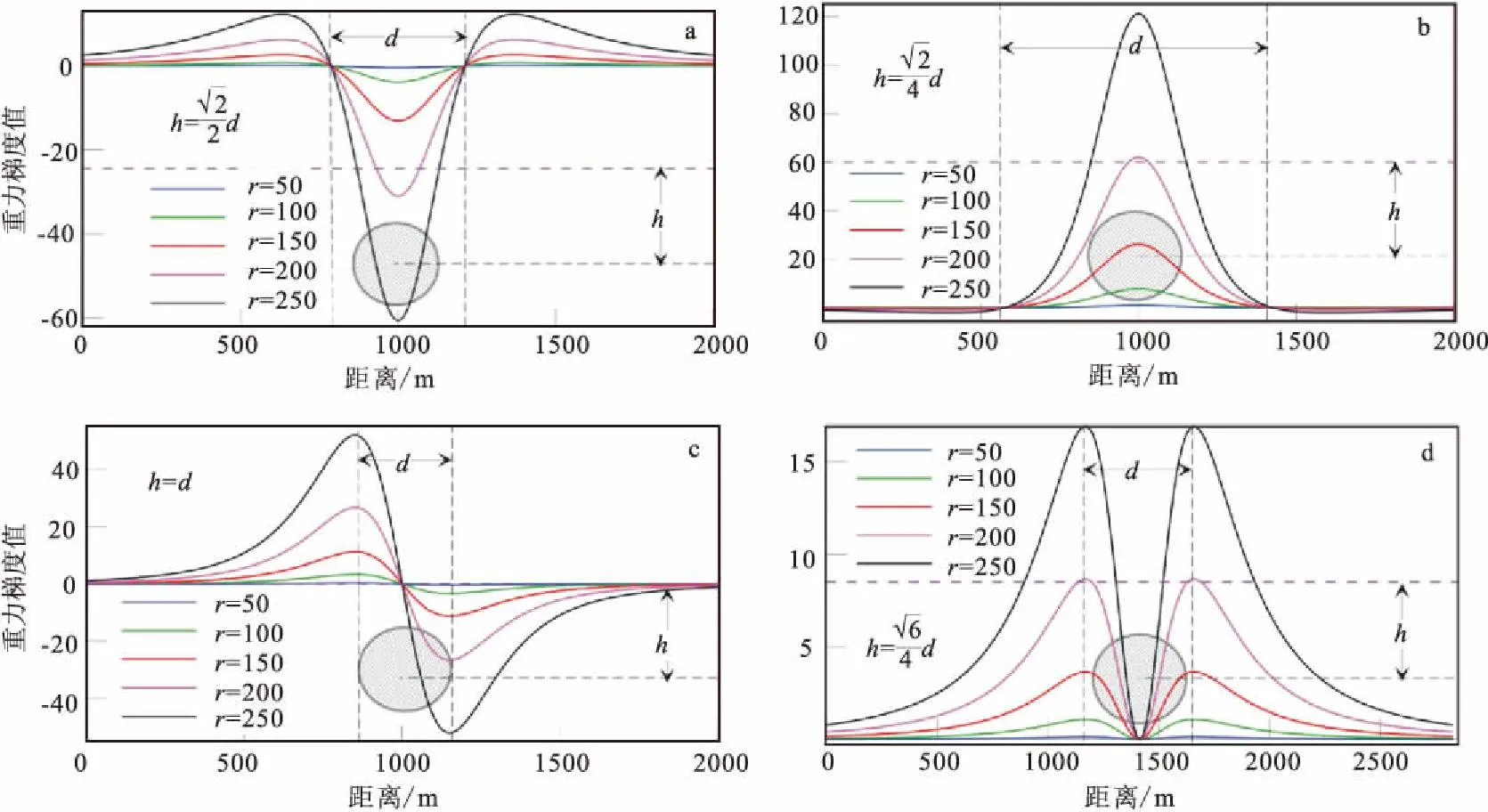
图7　不同半径的梯度张量主剖面曲线Fig.7　Main sections of gravity gradient tensors base on different radii(a)Uxx(Uyy)；(b)Uzz；(c)Uxz(Uyz)；(d)Uxy

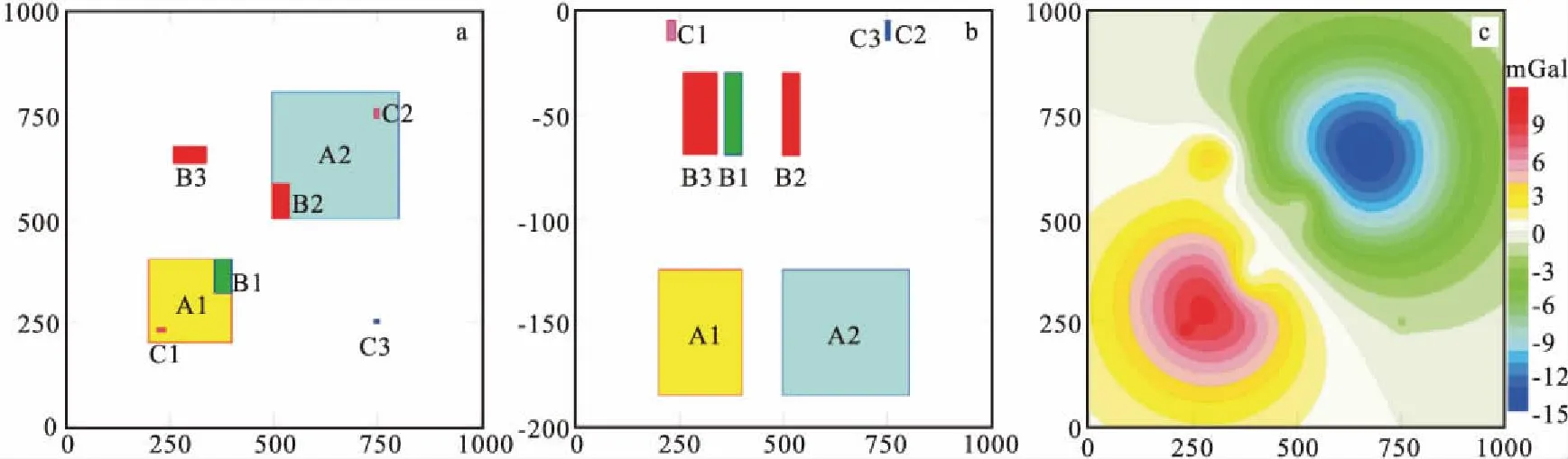
图8　组合模型在XOY平面和YOZ平面的投影以及重力异常等值线Fig.8　Projections of composite pattern in XOY plane and YOZ plane,and gravity anomaly contour of composite pattern(a)XOY;(b)YOZ;(c)重力异常等值线

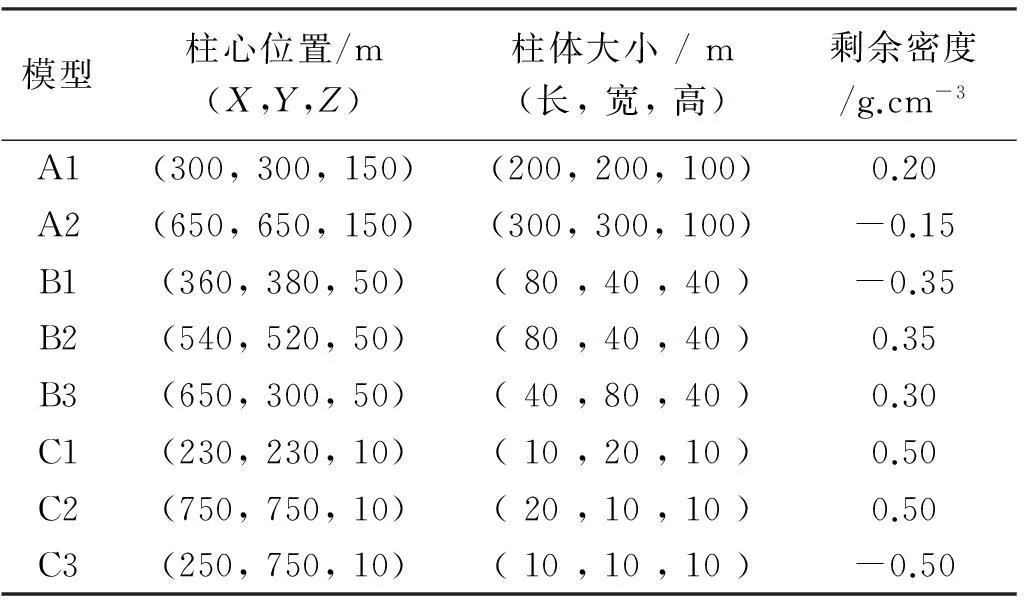
表2　组合模型中各棱柱体的几何参数Tab.2　Geometric parameter of each prism in composite pattern

应用重力梯度全张量正演计算，可得到组合模型的各个梯度分量异常，如图9所示。由于重力梯度张量对高频信息最为灵敏[1]，所以其对重力异常中较难识别的规模小、异常幅度大的高频信号识别效果十分明显。从图9中重力梯度各个分量中可以看到，规模最小、不易识别的模型C1、C2和C3在图9中以模型梯度张量的特征独立的呈现了出来，能够很地识别其位置；除了重力异常中独立的B3异常外，模型B1和B2也能在重力梯度张量中呈现独立的特征形态；而在重力异常中最容易识别的A1和A2异常，在重力梯度张量中虽能基本呈现应有的梯度张量特征，异常曲线却受到了其他异常的干扰而变得畸形、影响识别。上述分析说明，重力梯度全张量在识别复杂组合模型异常体的位置方面效果明显，尤其是对浅部的、规模较小的异常识别效果更加突出，体现了重力梯度张量相对于重力异常的优越性；但这也反映了重力梯度全张量在实际资料应用中的一个弊端，那就是由于重力梯度全张量对高频或甚高频信息十分灵敏，在实际重力资料处理中噪声的存在对张量分析效果的影响也会很大。

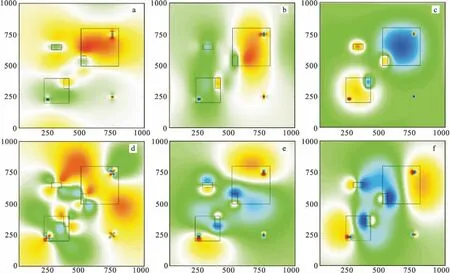
图9　组合模型的重力梯度张量等值线图Fig.9　Contour map of gravity gradient tensors base on composite pattern(a)Uxx；(b)Uyy；(c)Uzz；(d)Uxy；(e)Uxz；(f)Uyz

3结论

1)针对复杂模型正演计算的复杂性，利用有限单元法能很好地运用离散网格单元的叠加计算进行重力梯度全张量正演，并且有较高的精度。

2)在球体模型参数的识别方面，重力梯度全张量能够很好地识别模型水平面投影中心位置及中心埋深，对球体规模(半径大小)的识别不太明显。

3)重力梯度全张量能够减小模型体之间的相互干扰和影响，能很好地识别掩盖在埋深和规模较大的模型异常中的埋深和规模较小的模型异常，压制背景场而突出局部异常。

4)由于重力梯度全张量对高频信息很敏感，因此噪声的存在对实际资料处理和解释带来很大的影响，不利于噪声较大的实际资料处理，这也是重力梯度需要进一步研究和改善的一个方面。

参考文献：

[1]王谦身.重力学[M].北京:地震出版社,2003.

WANG Q S.Gravitology [M].Beijing:Seismological press,2003.(In Chinese)

[2]JAMES WHILE,ANDREW JACKSON,DIRK SM-IT,et al.Spectral analysis of gravity gradiometry profiles [J].Geophysics,2006,71(1):11-22.

[3]宁津生,罗志才,晁定波.卫星重力梯度测量的研究现状及其在物理大地测量中的应用前景[J].武汉测绘科技大学学报,1996,21(4):309-314.

NING J S,LUO Z C,CHAO D B.The present situation on satellite gravity gradiometry and its vistas in the application of physical geodesy [J].Journal of Wuhan Technical University of Surveying and Mapping,1996,21(4):309-314.(In Chinese)

[4]张永志,夏朝龙,王卫东,等.日本9.0级地震区重力梯度的时空分布[J].大地测量与地球动力学,2013,33(6):2-4.

ZHANG Y Z,XIA C L,WANG W D,et al.Temporal and space contribution of gravity gradients in Japan Mw9.0 earthquake area [J].Journal of geodesy and geodynamics,2013,33(6):2-4.(In Chinese)

[5]高春春,陆洋,史红岭.卫星重力梯度测量在海洋科学中的应用分析[J].海洋测绘,2012,32(5):77-81.

GAO C C,LU Y,SHI H L.Application analysis of satellite gravity gradiometry in ocean science [J].Hydrographic surveying and charting,2012,32(5):77-81.(In Chinese)

[6]舒晴,周坚鑫,尹航.航空重力梯度仪研究现状及发展趋势[J].物探与化探,2007,31(6):485-488.

SHU Q,ZHOU J X,YIN H.Present research situation and development trend of airborne gravity gradiometer [J].Geophysical &geochemical exploration,2007,31(6):485-488.(In Chinese)

[7]孟嘉春,蔡喜楣.卫星重力梯度测量及其应用前景探讨[J].地球物理学报,1991,34(3):369-376.

MENG J C,CAI X M .Approach on satellite gravity gradiometry and its vistas of applications [J].Chinese journal of geophysics,1991,34(3):369-376.(In Chinese)

[8]汪炳柱.用样条函数法求重力异常二阶垂向导数和向上延拓计算[J].石油地球物理勘探,1996,31(3):415-422.

WANG B Z .Computing the vertical second derivative and upward continuation of gravity anomaly by spline function method [J].Oil geophysical prospecting,996,31(3):415-422.(In Chinese)

[9]杨辉 王宜昌.复杂形体重力异常高阶导数的正演计算[J].石油地球物理勘探,1998,33(2):278-283.

YANG H,WANG Y C .Forward computation of high order derivative of gravity anomaly relating to comlplex geologic body [J].Oil geophysical prospecting,1998,33(2):278-283.(In Chinese)

[10]KEVIN L.MIEKUS,JUAN HOMERO HINOJOSA.The complete gravity gradient tensor derived from the vertical component of gravity:a fourier transform technique [J].Journal of applied geophysics,2001,46:159-174.

[11]张凤旭,孟令顺,张凤琴,等.重力位谱分析及重力异常导数换算新方法——余弦变换[J].地球物理学报,2006,49(1):244-248.

ZHANG F X,MENG L S,ZHANG F Q,et al.A new method for spectral analysis of the potential field and conversion of derivative of gravity-anomalies:cosine transform [J].Chinese journal of geophysics,2006,49(1):244-248.(In Chinese)

[12]曹书锦,朱自强,鲁光银,等.基于单元细分H-自适应有限元全张量重力梯度正演[J].地球物理学进展,2010,25(3):1015-1023.

CAO S J,ZHU Z Q,LU G Y,et al.Forward modelling of full gravity gradient tensors based H-Adaptive mesh refinement [J].Progress in geophy,2010,25(3):1015-1023.(In Chinese)

[13]曾华霖.重力场与重力勘探[M].北京:地质出版社,2005.

ZENG H L.Gravity field and gravity exploration [M].Beijing:Geological publishing house,2005.(In Chinese)

[14]MICHAEL S.ZHDANOV,ROBERT ELLISZ,SOUVIK MUKHERJEE.Three dimensional regularized focusing inversion of gravity gradient tensor component data [J].Geophysics,2004,69:925-937.

[15]王勖成,邵敏.有限单元法基本原理和数值方法[M].北京:清华大学出版社,1997.

WANG M C,SHAO M.Basic principle and numerical method of finite element method [M].Beijing:Tsinghua University press,1997.(In Chinese)

Forward calculation and analysis of gravity gradient tensors based on finite element method

PENG Jiang-yinga,WU Xinga,HAN Wen-wenb,LIU Kang-weia

(Chengdu University of Technology a.College of Geophysics,b.College of Geophysics Chengdu610059,China)

Abstract:Gravity gradient anomaly has many advantages relative to gravity anomaly,it is necessary to study gravity gradient tensors.In forward modeling of gravity gradient tensors,it is difficult to derive mathematical formulas of complex geological bodies.But finite element method has an advantage in volume integral,it can be used to quickly and easily do forward calculation for full tensors gravity gradient of complex geological bodies.By establishing models and forward calculating,we analyzed plane and section characteristics of gravity gradient anomaly of sphere model,and analyzed the relationship between gravity gradients and position of sphere model.Finally we utilized gravity gradients forward simulation of complex geological bodies,and illustrated the advantages and disadvantages of gravity gradients in finding out the position of geologic body.

Key words:full tensor gravity gradient;finite element method;forward calculation;anomaly recognition

收稿日期：2015-04-10改回日期：2015-05-25

基金项目:国家科技重大专项“十二五”(2011ZX05025-001-08)；地质调查项目(12120113095100)

作者简介：彭江英(1990-)，女，硕士，主要研究方向为深部地球物理与地球动力学，E-mail：wylxing@foxmail.com。

文章编号：1001-1749(2016)02-0151-09

中图分类号：P 631.1

文献标志码：A

DOI：10.3969/j.issn.1001-1749.2016.02.02