高密度聚乙烯土工格栅拉伸蠕变特性及模型分析

张　鹏，周志刚，杨志峰，谢晓如

(1.长沙理工大学道路结构与材料交通行业重点实验室，湖南　长沙　410004；2.江西省高速公路投资集团有限责任公司，江西　南昌　330000)

高密度聚乙烯土工格栅拉伸蠕变特性及模型分析

张鹏1，周志刚1，杨志峰2，谢晓如2

(1.长沙理工大学道路结构与材料交通行业重点实验室，湖南长沙410004；2.江西省高速公路投资集团有限责任公司，江西南昌330000)

关键词：土工格栅；拉伸试验；蠕变特性；本构模型；拉伸强度

0引言

高密度聚乙烯(HDPE)土工格栅是一种线型烯烃类聚合物，其以高密度聚乙烯(HDPE)为原料，加入一定量防紫外线、抗老化剂后，经挤出冲孔，并单向或双向拉伸而形成的新型土工合成材料。该材料因具有较之普通格栅更高的抗拉强度、更好的抗变形能力而被广泛应用于地基、路基、堤坝、边坡等土体结构的加固工作。近年来，随着工程实践的不断深入，加筋土应用技术得到了巨大的发展，但一些问题也逐渐暴露出来。如加筋土体中的土工格栅一直处于受拉状态，在长期荷载和温度的作用下将产生蠕变，这一现象会导致加筋体结构发生较大变形，并最终导致结构失效。因此，如何在设计时有效地考虑蠕变对加筋土体结构长期稳定性和强度的影响，一直是相关科技人员关注的问题。多年来国内外学者开展了一系列研究，如王钊[1]对土工合成材料的蠕变试验方法进行了系统的解释；栾茂田[2]通过开展不同荷载和不同温度下的蠕变试验得出温度对蠕变试验具有重要影响；丁金华[3]对HDPE土工格栅进行蠕变试验，研究了应力大小、环境温度、化学作用、施工损伤以及侧限约束等对格栅蠕变性能的影响；薛超[4]对两种型号的聚丙烯(PP)双向土工格栅进行相同应力水平下的蠕变试验，并在试验结束后卸载应力并观测两种格栅的收缩情况。前人在整理分析众多试验资料的基础上提出了一些经验型本构关系，如线性、双曲线和多项式等蠕变模型等[5]，并以此研究土工合成材料的长期使用性能。随着对土工合成材料蠕变性能研究的深入，人们基于热流变理论相继提出了多种流变理论本构模型。如Finnigan J A[6]由土工合成材料短期蠕变试验提出了一种对数型本构模型；栾茂田等[7]通过对土工格栅蠕变试验结果的分析整理，并借鉴Rabotnov对金属及塑料时间函数的研究，提出了反映土工格栅蠕变特性的本构模型；刘华北[8]通过土工合成材料循环加载试验，并结合应力粘塑性理论，建立了可以同时描述土工合成材料蠕变和应力松弛特性的统一本构模型；兰滔[9]采用三参数粘弹流变模型对格栅的蠕变进行模拟，并将格栅上各点的应力与流变模型进行耦合，得到了加筋体中考虑应力水平的格栅各点蠕变的三维图像。尽管在土工合成材料长短期蠕变性能及其本构模型方面已积累了众多宝贵的经验，但随着新型土工合成材料的发展，以往的研究成果能否科学合理地反映它们的长期蠕变性能，需要进一步研究论证。

本文所研究的土工格栅属于一种高强、低伸长率的新型土工合成材料，与以往土工格栅相比，它能更好地满足加筋土结构高强、小变形的需求。为了进一步促进这种新型土工格栅材料的推广应用，本文通过不同荷载水平下的恒载拉伸蠕变试验，对比分析荷载水平对其蠕变的影响，并应用已有的土工合成材料蠕变本构模型，对蠕变试验结果进行模型参数回归拟合，探讨相关蠕变本构模型的合理有效性。

1高密度聚乙烯土工格栅拉伸试验

1.1高密度聚乙烯土工格栅基本性能

试验所用土工格栅为湖北力特土工合成材料有限公司生产的高密度聚乙烯单向拉伸土工格栅，规格型号为：RS90PE1.1 m×50 m。格栅物理性质如表1所示。

表1　HDPE土工格栅物理性质表

1.2试验方法

参照《公路土工合成材料试验规程(JTG E50-2006)》[10]的要求对土工格栅进行拉伸试验，测试项目主要包括：极限拉伸强度、标称伸长率等。试验采用窄条拉伸形式，即对单肋土工格栅进行拉伸试验。

试验时土工格栅拉伸速率为10 cm/min。试验温度控制为20±1 ℃。为了防止夹具对土工格栅的损伤，在夹具内增设柔性护垫。

1.3试验结果分析

通过试验，得到HDPE土工格栅样条拉伸试验结果如表2所示。

表2　拉伸强度试验结果表

将表中试件1的拉伸结果绘制于图1。图中张力为试验荷载与试样受力宽度的比值，应变为试样拉伸长度与原长度的比值。

图1　拉伸强度试验结果曲线图

由图1可知，在试验初期土工格栅应变随张力近似线性增长，到达峰值后，随着土工格栅继续延长，张力略有下降，并呈现出一平台值，之后发生快速拉断。试验测得的土工格栅极限拉伸强度、屈服伸长率平均值分别为90.5 kN/m、11.07%。

2土工格栅拉伸蠕变试验

2.1拉伸蠕变试验方法介绍

试验参照《公路土工合成材料试验规程(JTG E50-2006)》[10]的要求进行。由于蠕变试验周期长，包括后续老化试件在内所有试件需同时进行试验，因成本、场地和避免扰动等原因，故在试验室的路基试槽中进行。即在试槽侧壁平行安装多根工字钢横梁，每根横梁上悬挂5个土工格栅试件，每个试件采用单肋拉伸蠕变的形式。试件间距需保证人员足够的工作空间，避免触碰其它试件及其加载装置。土工格栅的初始长度为100 cm，通过特定夹具将试件与横梁连接，下端采用托盘悬挂事先按要求称量好的重物。土工格栅的夹持位置应与夹具持平，以尽量保证加载后土工格栅受力均匀。悬挂重物时应注意加载速率不可过大，以避免对土工格栅造成冲击效应。选择3个张力水平，即极限拉伸强度的30%、40%、50%。每个张力水平下分别进行2组平行试验。试件的加载情况见表3。悬挂重物开始即在设定的时刻记录土工格栅的伸长量，并定时记录环境温度和湿度。按规范要求的时间间隔进行数据的收集，并根据试样伸长的快慢及时调整测试时间间隔，试验持续时间至少1 000 h以上。在试验期间，实测环境温度约22 ℃左右，湿度为55%～60%。

表3　拉伸蠕变试验加载情况表

2.2拉伸蠕变试验结果

由HDPE土工格栅拉伸蠕变试验数据绘制格栅时间-应变曲线，如图2所示。

图2　拉伸蠕变试验结果曲线图

由图2可知，试验初期土工格栅应变随着时间急剧增大，然后随着时间的推移逐渐趋于平缓，在测试时间内呈现为两阶段变形特征：第Ⅰ阶段在较短的时间内变形急剧发展，这一阶段主要以弹性变形为主，其后随着时间推移，逐渐产生黏性变形，并进入第Ⅱ阶段——稳定变形阶段，随着时间的推移，土工格栅变形近似线性平稳地增长。在较低张力水平下(如30%、40%)，土工格栅试件能较快地达到一个稳定的应变量，且该值稳定在10%以下。但当张力水平继续增大达到50%时，格栅试件在较短时间内即达到了10%的应变量，该应变量超出规范允许使用值(见《土工合成材料塑料土工格栅(GB/T 17689-2008)》[11])。因此应使此种土工格栅承受的张力水平荷载不超过50%。

3土工格栅拉伸蠕变经验型模型分析

3.1土工合成材料拉伸蠕变的经验型模型

结合国内外研究可知，当前用于预测土工合成材料蠕变行为的经验模型可以大致分为以下四种：幂函数与近幂函数，对数和近对数函数，双曲线函数，以及其它经验型函数[12][13]。

表4　土工合成材料拉伸蠕变经验型模型表

对上述公式中的蠕变速率型积分可以转化为相应的幂函数表达形式。由此可见当前使用的各类经验模型可以归纳为三种：幂函数、对数函数和双曲线函数[12]。

3.2土工格栅拉伸蠕变经验型模型参数求解与评价

根据土工格栅蠕变试验数据，对幂函数、双曲线函数、对数函数等三类典型的土工格栅拉伸蠕变经验型模型参数进行回归求解。结果如表5～7所示。

表5　幂函数模型参量回归结果表

表6　双曲线模型参量回归结果表

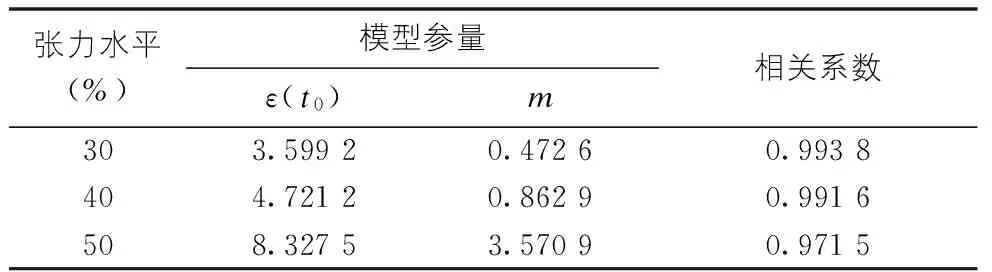
表7　对数函数模型参量回归结果表

表5～7中三种经验型蠕变模型反映初始变形的a、εi、ε(t0)均随着张力水平值的增大而增大，这与图2中蠕变曲线Ⅰ阶段变形特征一致。

对上述不同张拉水平下三类蠕变模型模拟的相关系数分别取平均值可得：幂函数型0.991 2，双曲线型0.964 8，对数函数型0.985 6。由此可知，幂函数型蠕变模型对实测结果的拟合最为接近。并且在同一种蠕变模型中，随着张力水平值增加，相关系数逐渐下降，表明蠕变模型更适用于低荷载水平的情况。

4土工格栅粘弹性本构模型分析

4.1土工格栅粘弹性本构模型

任何材料的变形由弹性、塑性和黏性三类变形组成，各自在总变形中所占比例因材料种类和荷载环境条件等因素而异。对于土工格栅之类高分子材料，除了弹性变形，其塑性和黏性变形也较为明显，符合热流变力学特征。前述的经验型蠕变模型不能很好地诠释土工格栅这种变形机制。为此，人们基于粘弹性力学理论，应用粘弹性本构模型来描述土工格栅拉伸蠕变行为。如通过引进更为直观形象的弹簧及粘壶元件，以串、并联的方式模拟其蠕变力学行为。基于这种思路人们相继提出了Maxwell模型、Kelvin模型、三参数粘弹性模型等常用的理论模型[14]。

Maxwell模型的组成形式是理想弹簧和理想粘壶的串联，在应力恒定的情况下模型内部两受力元件所受应力相同，应变量为两元件应变之和[13]。与之相对应的Kelvin模型是通过并联将一个理想弹簧和一个理想粘壶联系在一起，该模型结构中各元件应变值相等，应力值为各元件单元应力之和[14]。三参数粘弹性模型则是将Kelvin模型与弹簧元件串联得到的。

4.2土工格栅三参量粘弹性本构模型

由土工格栅蠕变试验结果可知，在重物加载瞬间土工格栅产生弹性变形，在恒定的应力作用下，格栅蠕变量进一步扩大，直到进入稳定状态后蠕变量维持在一固定水平。这一试验现象可以由三参数粘弹性本构模型加以描述。在荷载施加的初期，由于粘滞元件的特点，格栅形变并未引起Kelvin体的变化，因此形变量仅由弹簧元件提供；当保持σ不变，ε值不断扩大，Kelvin体开始发挥作用，这两部分的共同影响促使土工格栅的蠕变逐渐趋于稳定。

采用拉普拉斯变换与逆变换可以推导出三参量粘弹性本构模型蠕变表达式[15]：

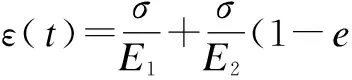
(1)

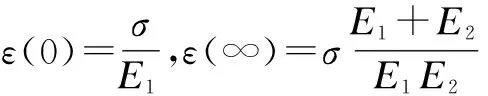
4.3模型参数求解与验证

基于麦夸特法及全局优化问题最优化求解理论[16][17]对低张力水平下(30%、40%)的土工格栅蠕变试验数据进行数值拟合，从而求出模型中的弹性系数E1、E2和粘滞系数η。

表8　三参数粘弹性本构模型参数回归值表

由表8所得的模型参数分别计算土工格栅的理论蠕变值，并与实测平均值进行对比。

由图3可知，三参数粘弹性本构模型能较准确地反映30%张力水平情况下土工格栅的蠕变过程，但当张力水平增大为40%时，其模拟效果不够理想，特别是蠕变后期。这一结果说明三参数粘弹性本构模型仅能反映低张力水平下的蠕变行为。

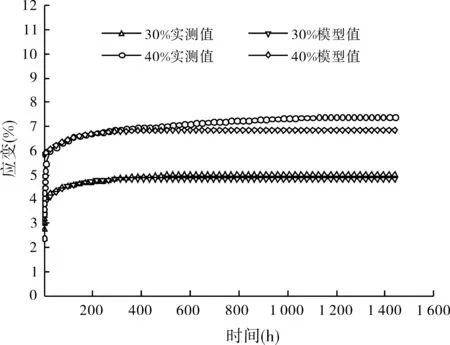
图3　土工格栅蠕变实测值与粘弹性模型值对比曲线图

5结语

本文相继开展了高密度聚乙烯土工格栅拉伸强度试验和拉伸蠕变试验，通过试验对该种新型土工合成材料的力学性能进行分析。最终结论包括：

(1)高密度聚乙烯土工格栅的极限拉伸强度远高于普通土工格栅的，而其屈服伸长率也较小，故其抗破坏和抗变形能力强。

(2)高密度聚乙烯土工格栅蠕变呈现为两阶段变形特征。Ⅰ阶段变形时间很短，以弹性变形为主；Ⅱ阶段能维持较长时间，属于稳定变形阶段。

(3)三类经验型蠕变模型中幂函数蠕变模型对试验实测值的拟合效果最佳；对于同一种蠕变模型，随着张力水平增加，其相关系数逐渐下降，因此三种典型模型均更适宜用于评价低张力水平下的蠕变行为。

(4)三参数粘弹性本构模型适用于反映低张力水平情况时土工格栅的蠕变过程。

参考文献

[1]王钊，李丽华，王协群.土工合成材料的蠕变特性和试验方法[J].岩土力学，2004，25(5)：723-727.

[2]栾茂田，肖成志，杨庆，等.长期荷载作用下土工格栅蠕变特性的试验研究[J].土木工程学报，2006，39(4)：87-91.

[3]丁金华，童军，张静，等.环境因素对土工格栅蠕变特性的影响[J].岩土力学，2012，33(7)：2048-2054.

[4]薛超，袁慧，刘双英，等.双向土工格栅的蠕变与收缩特性研究[J].太原理工大学学报，2015，46(6)：697-701.

[5]肖成志，栾茂田，杨庆，等.土工格栅经验型蠕变模型及其参数试验[J].中国公路学报，2006，19(6)：19-24.

[6]FinniganJA.Thecreepbehaviourofhightenacityyarnsandfabricsusedincivilengineeringapplications[C].ProceedingsoftheInternationalConferenceontheUseofFabricinGeotechnices.Paris，1977：305-309.

[7]栾茂田，肖成志，杨庆，等.土工格栅蠕变特性的试验研究及粘弹性本构模型[J].岩土力学，2005，26(2)：187-192.

[8]刘华北.土工合成材料循环受载、蠕变和应力松弛特性的统一本构模拟[J].岩土工程学报，2006，28(7)：823-828.

[9]兰滔.考虑应力水平的加筋土格栅蠕变研究[J].长江科学院院报，2015，32(7)：89-93.

[10]JTG E50-2006，公路工程土工合成材料试验规程[S].

[11]GB/T 17689-2008，土工合成材料塑料土工格栅[S].

[12]周志刚，李雨舟.土工格栅蠕变特性及其黏弹塑性损伤本构模型研究[J].岩土工程学报，2011，33(12)：1943-1949.

[13]Siriwardane H，Gondle R，Kutuk B.Analysis of flexible pavements reinforced with geogrids[J].Geotech Geol Eng.2010.28：287-297.

[14]周光泉，刘孝敏.粘弹性理论[M].合肥：中国科技大学出版社，1996.

[15]周玲.从三参数固体模型来理解高聚物的粘弹性[J].武汉科技学院学报，2008，21(2)：29-31.

[16]胡明伟，史其信.探讨回归分析在交通工程应用中的若干问题[J].公路交通科技，2002，19(1)：68-71.

[17]姜海波，李艳茹.通用回归分析模型[J].数学的实践与认识，2006，36(1)：174-180.

摘要：文章通过开展高密度聚乙烯土工格栅的拉伸强度试验和拉伸蠕变试验，比较张力水平大小对其拉伸蠕变的影响，并对不同类型土工格栅拉伸蠕变模型进行回归求解，以提出适用于高密度聚乙烯土工格栅拉伸蠕变的模型。结果表明，与普通土工格栅相比，高密度聚乙烯土工格栅具有很强的抗破坏和抗变形能力；所用的经验型蠕变模型和三参数粘弹性本构模型适用于反映低张力水平情况时的土工格栅蠕变行为；幂函数、双曲线函数、对数函数等三类经验型蠕变模型中幂函数型蠕变模型拟合土工格栅蠕变试验数据的精度最高。

Analysis onTensile Creep Characteristics and Model ofHigh-density Polyethylene Geogrid

ZHANG Peng1，ZHOU Zhi-gang1，YANG Zhi-feng2，XIE Xiao-ru2

(1.Key Laboratory of Road Structure and Materials Transportation Industry，Changsha University of Science & Technology，Changsha，Hunan，410004；2.Jiangxi Expressway Investment Group Co.，Ltd.，Nanchang，Hiangxi，330000)

Abstract：Through the tensile strength test and tensile creep test of high-density polyethylene geogrid，this article compared the influence of tension level on its tensile creep，and conducted the regression solving on the tensile creep model of different types of geogrids，in order to propose the model suitable for the tensile creep of high-density polyethylene geogrid.The results showed that，compared to the common geogrid，high-density polyethylene geogrid has a strong anti-sabotage and anti-deformation ability；the empirical creep modeland three-parameter viscoelastic constitutive modelbeing adoptedare applicable to reflect thegeogrid creep behaviorunder low tension situation；among three empirical creep models of power function，hyperbolic functions，and logarithmic functions，the power function creep model has highest fitting accuracy with geogrids creep experiment data.

Keywords：Geogrid；Tensile test；Creep characteristics；Constitutive model；Tensile strength

作者简介

基金项目

中图分类号：U417

文献标识码：A

DOI：10.13282/j.cnki.wccst.2016.04.001

文章编号：1673-4874(2016)04-0001-05

收稿日期：2016-03-28

张鹏(1991—)，硕士研究生，研究方向：道路工程；

周志刚(1966—)，教授，博士生导师，研究方向：道路工程；

杨志峰(1976—)，工程硕士，高级工程师，主要从事公路工程建设管理工作；

谢晓如(1970—)，高级工程师，主要从事公路工程建设管理、维修养护和技术研究工作。

江西交通科技计划项目“生态型土工格栅加筋土挡墙关键技术研究”(2015C0006)