*1组合赋权法在聚类分析中的应用

刘　群,冯长焕

(西华师范大学 数学与信息学院,四川 南充 637009)



*1组合赋权法在聚类分析中的应用

刘群,冯长焕

(西华师范大学 数学与信息学院,四川 南充 637009)

〔摘要〕文章选取了四川省某县(区)公安局对当地18个镇基于“一标三实”部分项目的考核得分,采用加权聚类分析的统计方法对数据进行分析．综合考虑各种赋权法的优缺点,最后采用组合赋权法对各项指标进行赋权．通过分析,将该市18个镇做了一个很好的归类．

〔关键词〕聚类分析；加权欧氏距离；组合赋权法

0引言

“一标三实”是指全面核查和采集全区标准地址信息、实有人口信息、实有房屋信息和实有单位信息．“一标三实” 基础信息采集录入,着力破解人、房、业等基础管理底数不清、情况不明的难题,以实现“以房找人、以人找房、查房知人、查人知房”的总体目标,提高公安机关对基本治安要素的管控能力,夯实公安工作和社会管理基础,为公安实战、社会管理、党政决策、服务民生提供基础信息支撑,以此逐步建立起与经济社会发展水平、人民群众需求相适应的基础信息管理新体系．完善好“一标三实” 基础信息的录入对公安机关是十分有必要的．而在实际的信息采集中,每个镇并不是百分之百地落实了该项工作,完成的好坏程度不同,基于这些因素,公安机关对此制定了“一标三实”考核得分表,对每项考核项目都有相应的得分和扣分细则,最后通过每月考核得到各镇对应的得分表．通过对各镇“一标三实”的得分情况,本文采用加权聚类分析的统计方法对此进行分析,最后对18镇进行了科学合理的分类．

1聚类分析

聚类分析[1](Cluster Analysis)是根据“物以类聚”的原则,研究对象的个体特征,把个体特征比较接近的样本聚集成一类的方法．聚类分析在经济、管理、社会学、医学等领域都有着广泛应用．聚类方法有很多,其中最常用同时也是比较成熟的一种聚类方法是系统聚类法．系统聚类法[2]的基本思想是:设共有n个样品,开始将每个样品单独成一类．先求出类与类即样品与样品之间的距离,找出距离最近的两类,将他们合并成一类,构成n-1类．然后在求出类与类之间的距离,将距离最近的两类合并成一类……这样一直下去,每次类别减少1个,直到所有样品合为一类为止．

2求解最优组合权重系数

传统的聚类分析在分类过程中假设待分类样本的指标对聚类结果的贡献相同．而Bezdek[3]指出由于对每个样本的特征提取不够完善,所以每个分量对样本聚类的贡献程度是不均的．在实际应用中我们也发现,各指标间具有差异性,对聚类结果的影响程度不同,所以在聚类分析过程中对指标进行加权是有必要的[4]．目前确定权重系数的方法有主观赋权法、客观赋权法[5]．其中常用的主观赋权法有层次分析法(AHP法)、TACTIC法、特尔斐法(Delphi法)、最小平方法等．常用的客观赋权法有夹角余弦法、主成分分析法、熵技术法等．主观赋权法的随意性较大,受主观因素影响较大,而客观赋权法需要通过数学理论知识计算而得,遵循严格的计算规则,但有时计算结果没有实际意义,无法解释．为了让权重系数更合理、更科学,许多学者提出了综合主、客观赋权法的组合赋权法[6]．本文运用不同赋权法得到的权重系数按照离差平方和最大的优化原则[7]对指标进行赋权,使得评价结果更加科学、合理．

2.1数据标准化处理

对m个样品的n个评价指标测得的数据记作:A=[aij]m×n,其中,aij表示第i个样本第j个评价指标的值,评级指标一般分为成本型、效益型．成本型指标是指数值越小越好的指标,效益型指标是指数值越大越好的指标．对于矩阵A对其进行如下无量纲化处理:

(1)

(2)

2.2组合权重系数

设n个评价指标有l种不同赋权方法对指标进行赋权,记第k种赋权方法给出的权系数向量为:Wk=(wk1,wk2,…,wkn)T,k=1,2,…,l.

综合考虑各个赋权方法的优缺点,采用组合权系数向量:

(3)

令矩阵Wn×l=(W1,W2,…,Wl),Θl×1=(θ1,θ2,…,θl)T,W为l个权系数向量组成的矩阵．

则(3)式可表示W*=WΘ．由组合赋权法得到的权重计算出第i个方案的综合评价值为:

(4)

一般而言,Di越大表示i第个方案越优．

2.3确定最优组合权重系数

采用各决策方案的综合评价值的离差平方和最大优化原则[8],求得W*的最优解．其基本思路为:记第i1个方案的综合评价值Di1与第i2个方案的综合评价值Di2的离差为:

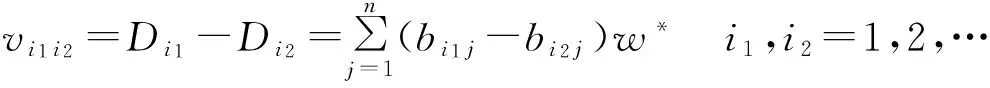
设表示第i个方案的综合评价值与其他各指标综合评价值的离差平方和,即:

则m个方案的离差平方和可表示为:

若令n×n阶矩阵B1为:

由此可将目标函数表示为:J(W*)=W*TB1W*=(WΘ)TB1(WΘ)=ΘTWTB1WΘ,目标函数转换成了和Θ有关的函数,可记为F(Θ)．基于m个方案总的离差平方和最大化优化原则,上述问题转换成如下优化问题:

maxF(Θ)=ΘTWTB1WΘ

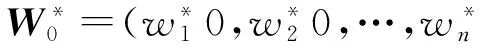
3加权聚类的实证分析

3.1数据获取与分析

四川省某县(区)公安局基于“一标三实”,从2013年10月到2014年4月,对当地18个镇的标准地址、实有单位、实有人口、质量考核这4个指标每月进行一次考核, 矩阵A是获取的考核成绩,其中各项考核指标总分均为10分．

3.2对数据规范化处理

根据(1)式和(2)式求出规范化属性矩阵B=(bij)18×4,

3.3求解最优权重系数

对于多指标评价问题,指标权重的确定有不同的方法,并且不同的方法存在各自的优点和缺点．主观赋权法体现了评价者的知识经验和主观愿望,但随意性较强．而客观赋权法运用了严谨的数学理论知识,但不能体现主观信息,有时甚至无法解释．本文选取一种主观赋权法和一种客观赋权法,综合二者考虑,运用离差平方和最大优化原则,确定最终的权重系数．

根据定义并运用MATLAB求出矩阵B1=(b1ij)4×4如下:

评价者给出的主观权重向量为W1=(0.30,0.15, 0.20, 0.35)T,运用夹角余弦赋权法[10]求出的客观权重向量为W2=(0.31, 0.12, 0.19, 0.38)T,由W1,W2组成4×2的分块矩W=[W1,W2]．

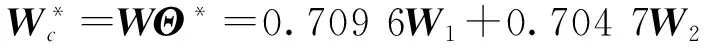
3.4基于组合赋权法进行加权聚类分析

图1　使用平均联接(组间)的树状图

通过图1可以看出,将8个镇分成四类较为合理．其中第一类是会龙、长乐、青居、走马、龙门;第二类是都京、航空港、青松、浸水、阙家、白塔、东观;第三类是江陵、小龙、老君、江东、胜观;第四类是安汉．至此,我们已经对18个镇进行了比较科学合理的分类,但还不能确定哪一类最好,哪一类最差,因此还需要对这四类进行优劣评价．根据(4)式求出各镇的综合评价值,得到了综合评价值矩阵:

通过计算得到这四类的综合评价值的均值分别为:第一类:0.90;第二类:0.68;第三类:0.57;第四类:0.22．

3.5聚类结果分析

通过上述分析可以得出聚类分析的结果:第一类会龙、长乐、青居、走马、龙门,综合评价值的均值为0.90,是四类中评价值最高的一类,说明这几个镇在“一标三实”这项工作中发挥最为出色;第二类是都京、航空港、青松、浸水、阙家、白塔、东观,综合评价值的均值为:0.68,是仅次于最好的一类,说明这几个镇认真完成了这项工作;第三类是江陵、小龙、老君、江东、胜观,综合评价值的均值为0.57,属于较差类,可以对这几个镇予以提醒;第三类安汉,综合评价值为0.22,属于最差一类,应该对此进行批评．这些数据可以为各镇评优评奖做一定的参考．

4结论

本文基于四川省某县(区)公安局基于“一标三实”对当地18个镇部分指标进行的考核得分进行实证分析,由于每个评价指标对评价结果的贡献程度不同,本文对评价指标进行了加权处理,使得评价结果更加科学合理．综合考虑各种赋权方法的优缺点,选择组合赋权法对评价指标进行赋权,在此基础上进行加权聚类分析,最后将这18个镇将他们分成了四类．通过对这四类的综合评价值的均值比较,对它们进行了优劣判断．通过对指标的加权处理,使得聚类分析结果更加科学、合理．

参考文献：

[1]马庆国.管理统计[M].北京:科学出版社,2002:261

[2]刘剑平,朱坤平,陆元鸿.应用数理统计[M].上海:华东理工大学出社,2012:213

[3]BEZDEK J C.Pattern recognition with fuzzy objective function algorithms[M].New York:Plenum Press,1981

[4]高新波.模糊聚类分析及其应用[M].西安:西安电子科技大学出版社,2004

[5]叶义成,柯丽华,黄德育.系统综合评价技术及其应用[M].北京:冶金工业出版社,2006:30-45

[6]张峰.谢振华.程江涛,等.基于向量皮尔森相关系数的组合赋权法[J].火力与指挥控制,2015(5):63-64

[7]王应明.离差平方和的多指标决策方法及其应用[J].中国软科学,2000(3):110-113

[8]李永宾,张凤鸣,李俊涛.基于组合赋权方法的多目标威胁排序[J].空军工程大学学报(自然科学版),2007,8(2):7-9

[9]陈华友.多属性决策中的一种最优组合赋权方法研究[J].运筹与管理,2003(2):8-9

[10]戴秋亮.基于夹角余弦赋权的地区经济发展的模糊综合评价研究[J].商丘职业技术学院学报,2010(1):49-50

Empirical Analysis of Weighted Euclidean Distance Correction

LIU Qun,FENG Changhuan

(College of Mathematics and Information, China West Normal University, Nanchong 637009, China)

〔Abstract〕This paper selects the Sichuan Province(District) Public Security Bureau of the 18 local towns assessment score that based on "standarized address and three facts" part of the project.Analysis of the data using statistical method of weighted clustering analysis.The advantages and disadvantages of various weighting methods are considered.Finally, the combination weighting method is used to weight the indicators.Through analysis, the city 18 towns to do a very good classification.

〔Key words〕cluster analysis; weighted euclidean distance; cosine weighting method

*收稿日期：2015-09-20

基金项目：西华师范大学基本科研业务费专项资金资助(14C004);南充市社科规划一般规划(NC2013B027).

作者简介：刘群(1989-),女,四川资阳人,西华师范大学数学与信息学院在读硕士研究生,主要从事概率论与数理统计.

〔文章编号〕1672-2027(2016)01-0001-05〔中图分类号〕O213.9

〔文献标识码〕A