FSAE赛车悬架分析与优化设计

李天然，童梅，张冬忠（长安大学汽车学院，陕西 西安 710064）



FSAE赛车悬架分析与优化设计

李天然，童梅，张冬忠
（长安大学汽车学院，陕西 西安 710064）

摘要：利用ADAMS软件建立某高校FSAE赛车双横臂悬架的仿真模型，并对模型进行动力学仿真得到表征悬架动力学性能的参数线图，针对这些参数进行分析并确定优化方向及目标，再利用ADAMS/insight模块来设定设计变量、综合目标函数和约束条件进行多目标优化设计，并根据优化结果修改仿真模型比较优化前后悬架的动力学性能，结果表明优化后的悬架模型在动力学性能方面明显有所提高，证明了多目标优化设计的正确性和有效性。

关键词：FASE赛车；双横臂悬架；Adams；建模仿真；优化设计

10.16638/j.cnki.1671-7988.2016.05.004

CLC NO.: U463.3Document Code: AArticle ID: 1671-7988(2016)05-38-03

引言

FSAE（formula SAE赛车比赛）是一项由学生参与的工程设计竞赛，各参赛车队按照赛事规则及标准，以1年为周期，设计并制造出一辆小型单人座休闲赛车。对于FSAE赛事来说，悬架的设计时一项非常重要的工作，其控制车轮的运动的目的是如何发挥最大的附着力、抵抗侧倾和纵倾以及校核悬架的安全性等，而轮胎是唯一直接接触地面的车身部件，你可以想象让轮胎以适当的方式接触地面有多么重要，不论遇到什么样的路面状况或在任何速度下都要让赛车始终处于控制之中[9]，本文以FSAE赛车悬架为研究对象，利用adams对其进行仿真，从而达到优化的目的[2]。

（1）双横臂独立悬架的建模

FSAE赛车的悬架通常是采用不等长双横臂加推杆减震机构的形式，悬架具有左右对称性，其中包括虚拟主销、上A型臂、下A型臂、推杆、摇臂、减震器、稳定杆拉臂、横向稳定杆等结构[8]。由于FSAE赛车悬架是左右对称的，根据硬点坐标建立前悬架一侧的模型[5]并根据悬架运动添加约束，并且将定位参数如主销内倾角、主销后倾角、前轮前束、车轮外倾角的变化量等作为测量函数，再将各硬点坐标设置为设计变量DV1、DV2、DV3……DVn，再创建轮跳试验台完成初步建模。

（2）前悬架性能仿真

想要设计出性能良好的FSAE赛车悬架结构，必须要研究悬架运动特性的变化规律，例如赛车在直线行驶时两侧轮胎是同向跳动的，而在赛车过弯道时，车身发生一定的侧倾，这时的两侧悬架的跳动方向是相反的，所以在Adams中建立的试验台能够简化这一过程，在轮跳实验中我必须对前轮定位参数[3]及其它性能参数相应的变化规律并得到在车轮垂直跳动行程悬架各性能参数的变化曲线加以分析[4]。

将激振台架上下激振位移设置为30mm，使左右车轮同向上下跳动，计算悬架的性能参数的变化规律。

车轮外倾角的变化范围在（-1.92°~-0.24°），车轮跳动时外倾角的变化影响着轮胎与地面的接触姿态，为了得到良好的附着性，其目标是尽量使外倾角在上跳时减小，下跳时增加，保证轮胎在过弯时与地面垂直得到更好的附着力的同时避免车轮相对车身跳动时的外倾角变化过大[6]，外倾角随车轮跳动的变化曲线，如图1所示。

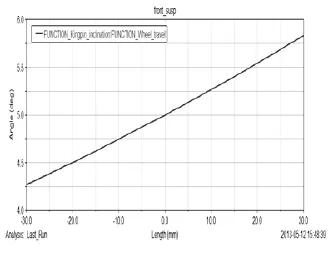
图1　外倾角变化曲线

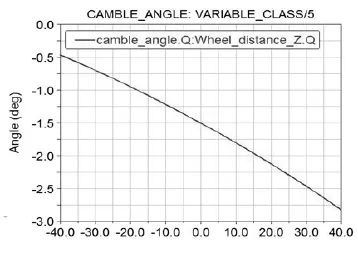
图2　内倾角变化曲线

主销内倾角的变化范围在（4.26°~5.77°），内倾角不仅影响转向盘对车手的感觉，而且能降低转向力矩，产生由车身重力引起的低速稳定回正力矩，当主销内倾角越大，转向时对车身的抬升作用就越明显，同时主销内倾角会使转向时车轮的外倾角变大[6]，这种变大的趋势不利于车轮实现更好的抓地，所以变化不宜过大，内倾角变化曲线，如图2所示。

主销后倾角的变化范围在（2.497°~2.504°），主销后倾角可以使赛车保持直线行驶；转向时产生有利于轮胎抓地的外倾角变化趋势，过大的主销后倾角会使机械拖距很大从而会淹没轮胎到达极限时的回正力矩突变信号[6]。而后轮不会转向之所以设置有后倾角是因为虚拟主销的位置以及弹性变形的影响，所以设置有后倾角来保持稳定。其变化曲线图如图3所示。

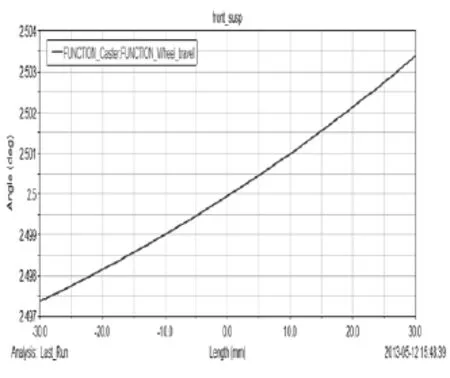
图3　后倾角变化曲线

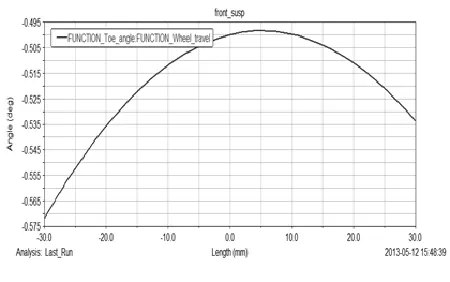
图4　前束角变化曲线

前束角变化范围在（-0.57°~-0.49°），前束角的变化过大会影响直线行驶的稳定性和加剧轮胎的磨损[6]，所以在设计原则上其变化应该尽可能的小。变化曲线图如图4所示。

1、多目标优化设计

在悬架运动仿真中当性能参数不能够满足我们设计的要求时，可对相应的硬点坐标进行调整，但是由于各个参数之间有着相互的影响[7]，所以给设计上带来了较大的难度和工作量。利用ADAMS/INSIGHT模块进行多目标优化，一般过程是对悬架的部分硬点坐标进行多次修改迭代（把硬点坐标看成设计变量），将悬架各部件尺寸跟硬点坐标联系起来（建立部件的参数化过程，部件会随硬点坐标的变化而变化），达到优化定位参数的目的。

1.1设计变量和参数化

在优化之前，首先要确定设计变量，性能参数是因变量是我们需要优化的量，所以将硬点坐标设置为设计变量，例如上A型臂前点XYX坐标分别设为DV_1、DV_2、DV_3变量，依次设置上A型臂后点XYZ坐标、下A型臂前点XYZ坐标等等作为设计变量。接下来就是参数化过程，在优化过程中设计变量是会不断修改迭代变化的，那么根据这些硬点坐标建立的模型部件也应该随之变化，编写带入设计变量DV_的函数式子，使其满足变化要求。

1.2敏感度

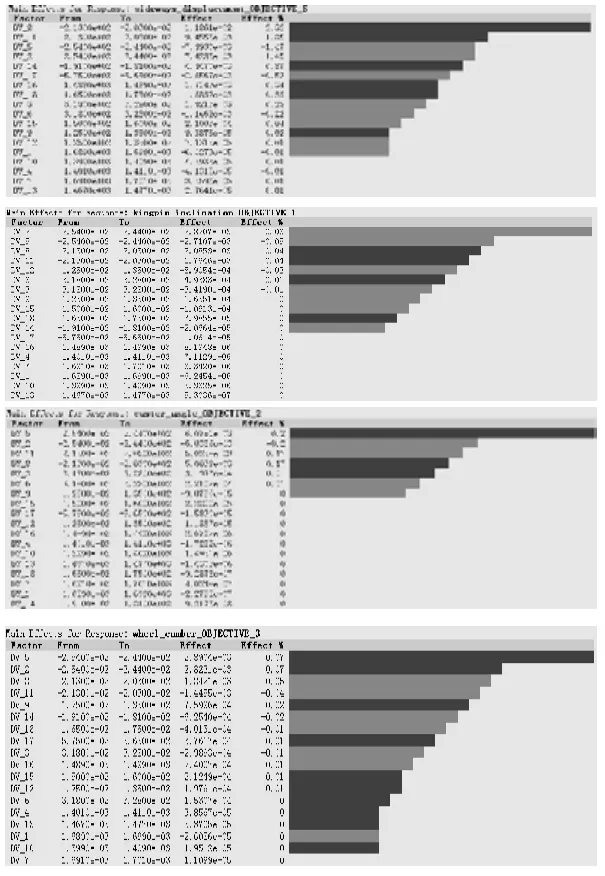
图5

在优化过程如果对其全部进行分析，会增加很多不必要的工作量，利用INSIGHT模块DOE分析，可以得出不同的设计变量在一定的范围内对优化目标响应的影响程度，本文对上述5个参数：外倾角、内倾角、后倾角、前束角、进行因素响应分析，上图给出了对这些参数影响较大的几个设计变量的结果。

根据上图参照可得出修改、调整影响较大的硬点坐标值作为设计变脸来进行优化设计，DV_2、DV_5、DV_8、DV_14对定位参数影响大，其实所有标量对所有目标值都有或多或少的影响，但是这些值更重要的作用是来适应结构的要求，确定其为最终的设计变量，其余坐标固定不变。

1.3约束条件

由于FSAE赛车采用的是钢架管阵车架，悬架的A型臂是通过安装吊耳焊接在车架钢管上面的，也就是说A型臂与车架连接点的坐标是受到空间结构上的限制的，所以在进行迭代优化时，坐标值得变化是有上下限制的，此外，由于转向机构、轮边立柱与悬架系统都是相互联系的，为了不发生干涉现象，设计变量基于初始值的变动量范围限制在（-5mm—+5mm）之间。

2、优化后的分析结果

优化后车轮定位参数随车轮跳动变化曲线，如下图所示。

图6　优化前后主销内倾角变化

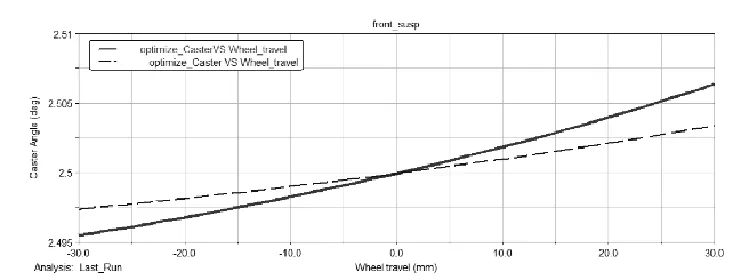
图7　优化前后主销后倾角变化

图8　优化前后车轮外倾角变化

图9　优化前后前束角变化

由曲线可以看出，优化后的车轮和主销参数变化更为合理，其中外倾角变化量比优化前的3°减小到1.5°，而且满足随车轮上跳时朝负值方向变化，下跳朝正值方向变化的设计要求；内倾角变化量较优化前2.85°减小到1.25°，且也满足设计要求；后倾角变化量从优化前的0.1°减小到0.05°，且变化趋势对整车操稳性有力符合上跳增加、下跳减小的设计要求，起到了补偿急刹和急加速造成的变化量；前束角的变化量减小到0.05°范围内，减小了磨胎且负前束配合负外倾角有利于跳动时外倾角的变化趋势趋于垂直于地面。对前悬架进行多目标优化设计后，各个参数随车轮跳动的变化范围都减小了且在接受范围内，总体来说，前悬架的多目标优化设计有显著提高性能的结果，同时也验证了其方法的有效性和正确性。

3、总结

近年来随着FSAE赛事的发展，越来越多的高校加入其中，在不久的将来也会有更多的高校及爱好赛车的组织加入其中，为了节省时间和金钱，我们可以利用ADAMS建立FSAE赛车模型并进行仿真优化设计，利用Adams/insight模块通过设定设计变量，综合目标函数和约束条件进行多目标优化设计并且得到的优化悬架综合性能得到明显提高，且利于开发和设计满足规则和需求的FSAE赛车，为FSAE赛车悬架设计制造和调试提供指导参考作用。

参考文献

[1]余志生.汽车理论[M].北京:机械工业出版社, 2002.

[2]刘虹,王其东.基于ADAMS双横臂独立悬架的运动学仿真分析[J].合肥工业大学学报,2007, 30(1):57-59.

[3]于海峰,于学兵.基于ADAMS的双横臂独立悬架优化仿真分析[J].机械设计与制造,2007(10):56-58.

[4]郭孔辉.汽车操纵动力学[M].长春:吉林科学技术出版社,1991.

[5]MILLIKEN W.F., MILLIKEN D. L,Race Car Vehicle Dynamics[M]. Warren dale SAEInternational,1994.

[6]鸠田幸夫,渡边衡三，关根太郎.汽车设计制造指南[M]. 王利荣等译,北京:机械工业出版社,2011.1.

Formula SAE Car Suspension Analysis and Optimization Design

Li Tianran, Tong Mei, Zhang Dongzhong
( University of changan automobile institute, Shaanxi Xi 'an 710064 )

Abstract：ADAMS software is used to establish the simulation model of a university's FSAE racing double arm suspension, and the parameters of the suspension dynamic performance are analyzed and the optimization directi- on and target are analyzed. Then the dynamic performance of the suspension model is improved. The results show that the optimization design is correct and effective.

Keywords:FASE racing; Double arm suspension; Adams; Modeling simulation; Optimization design

中图分类号：U463.3

文献标识码：A

文章编号：1671-7988（2016）05-38-03

作者简介：李天然，就读于长安大学汽车学院。