基于显式动力学有限元法的汽车盘式制动器仿真研究
成林,王谷娜,王茂美(北京电子科技职业学院,北京 100176)
基于显式动力学有限元法的汽车盘式制动器仿真研究
成林,王谷娜,王茂美
(北京电子科技职业学院,北京 100176)
摘要:根据制动盘与摩擦片的实际几何尺寸,建立制动工况下三维瞬态温度场-应力场仿真的计算模型。在考虑制动盘与摩擦片之间摩擦特性的基础上,运用有限元软件 ABAQUS 中的显式动力学模块,对盘式制动器的制动过程进行了动态的模拟,揭示了制动过程中制动盘瞬态温度场-应力场的分布规律,发现二者之间存在着耦合关系,二者随制动时间呈现周期性变化。
关键词:显式动力学;有限元法;盘式制动器;仿真研究
10.16638/j.cnki.1671-7988.2016.05.003
CLC NO: U463.51+2Document Code: AArticle ID: 1671-7988 (2016)05-09-04
前言
制动器广泛应用于飞机、火车、汽车等各类交通工具中,是一种交通安全装置。盘式制动器制动因数与摩擦系数成线性关系,具有制动性能稳定,力矩容量大和有利于程序化控制等突出的优点,已成为目前最先进的制动装置之一。

图1 盘式制动器三维模型
制动器制动过程中的温度场-应力场的变化规律对制动性能有很大影响,摩擦片各种形式的损坏的主要原因是摩擦所产生的热量超过了摩擦材料的极限热容量[1]。摩擦热导致摩擦材料发生热降解、粘结剂气化,摩擦因数发生变化,制动性能降低,出现热衰退现象;也使金属对偶件发生局部材料的相变与热变形,出现局部热点。局部热点的出现导致制动压力不均匀分布的进一步发展,这反过来又促进局部温度进一步升高,使制动器出现热弹性不稳定现象。在热应力作用下很容易造成材料的热衰退和破坏,产生初始裂纹并导致表面刮削现象加剧[2]。而热弹性失稳的出现,使得制动器摩擦振动与噪声加大。由于摩擦热的产生与接触压力的大小直接相关,而温度分布的不均匀性导致物体的热变形差异又直接影响接触状态或接触压力,接触状态的改变反过来影响摩擦热流输入强度[3]。可见摩擦制动器的热问题是应力场与温度场耦合问题。
本文按照制动盘与摩擦片的实际几何尺寸,把盘、片作为一个整体,建立了制动工况下三维瞬态温度场-应力场统一的有限元模型,利用显式动力学有限元法,仿真了制动器的制动过程,并考虑了摩擦热流在盘片之间的耦合问题,以及热源移动速度可变效应对制动盘热应力分布的影响。
1、显式动力学有限元法
传统的有限元法在算法上属于静态隐式算法。求解中每个时间步都要重新计算大型非线性刚度矩阵,并进行反复迭代以获得收敛解。需要较长的计算时间和较大的存贮空间。限于当前计算机的速度与容量,求解高度非线性的盘式制动器摩擦生热问题一直局限于二维或较小宽厚比的三维情况。基于显式算法的显式动力学有限元法克服了静态隐式有限元法收敛困难,计算时间长,存储空间大,接触与摩擦难于处理等的缺陷,能有效处理大规模接触和高度非线性问题[4]。显式动力学有限元法的基本方程为:

式中M表示质量矩阵;C表示阻尼矩阵;F表示内力矢量;R表示外载荷矢量;分别表示节点速度和加速度矢量。
通常采用中心差分法求解式(1.1)。tn时刻的离散速度和加速度中心差分公式分别为:

式中u表示位移。
把式(1.2)、(1.3)代入式(1.1),得到求解各离散时间点位移的递推公式为:

中心差分法是一种显式算法,它要求条件稳定。当利用它求解具体问题时,时间步长必须小于由该问题求解方程性质所决定的某个临界值∆tmin,否则算法不稳定。
根据Courant-Friendrichs-Levy稳定性准则,临界时间步长可由下式确定,即:

式中ωmax表示系统的最大固有频率;L表示单元特征长度(等于单元中任意两节点间的最小距离);c表示材料中的声速(与材料的性质有关)。对于三维单元,材料中的声速为:

2、温度场-应力场耦合问题计算模型的建立
要研究制动器工作过程中的温度场,必须建立摩擦生热模型,而摩擦生热问题是一种典型的温度场-应力场耦合问题。
2.1热传导模型的建立
建立热传导模型时,作以下假设[5]:
(1) 制动过程中,摩擦符合库仑定律,摩擦因数保持不变。
(2) 制动压力均匀作用于摩擦片,制动器内外两侧的片所产生的热负荷相等,即温度场-应力场对称于盘中心平面,因此只需考虑盘的一侧。
(3) 为解决摩擦热流在盘片之间的分配问题,考虑摩擦热流耦合问题。假设接触界面为理想平面,且在接触区域盘、片界面对应点瞬时温度相等;这样,摩擦热流密度q( x , y , t )根据界面的理想热传导和盘片的热物理性质在盘片之间自然分配;并且考虑热辐射影响。
(4) 不考虑材料磨损的影响,认为所有的摩擦功都转化为摩擦热,并且在计算时,把盘、片的热流输入当作边界热流输入处理,则摩擦表面输入热流密度满足:式中:表示摩擦表面上的比压;μ表示摩擦因数;v( x , y , t )表示盘、片的相对移动速度。

(5) 盘及片的材料为各向同性材料,由于单次紧急制动时间较短,材料热物性参数不随温度变化。
根据实际情况,认为片固定不动,而盘作逆时针转动。可得盘、片在直角坐标下的热传导方程:

式中dρ、ρp表示盘、片的材料密度;cd、cp表示盘、片的比热容;dλ、pλ表示盘、片的热导率;Td、Tp表示盘、片的温度;t表示制动时间。
制动盘的内圆侧面与轮轴凸缘盘相连,又与摩擦热流输入区域相距较远,对于紧急制动工况,其热流作用时间短,该表面是绝热的;制动盘的中心平面也是绝热的。摩擦片的背面远离摩擦面且与钢背相连,是绝热表面。
2.2热应力的计算
首先假设材料在制动过程中只发生线弹性变形。物体由于热膨胀只产生线应变,剪切应变为零。这种由于热变形产生的应变可以看作是物体的初应变。计算应力时包括初应变项:

式中σ表示材料的应力矩阵;D表示材料的弹性矩阵;ε表示材料的应变矩阵;表示温度变化引起温度应变。
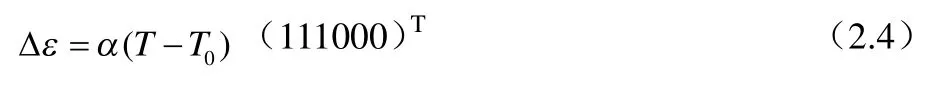
式中α表示材料的热膨胀系数;T0表示结构的初始温度场,假定是均匀的;T表示制动时结构的温度场。
2.3位移边界条件
根据实际情况,这里认为片不动,盘做逆时针转动。由于制动压力作用在摩擦片上,摩擦片是固结在制动钢背上,故对摩擦片施加x,y轴两个方向的固定约束。
根据假设条件(2),认为盘的中心平面沿z方向轴向固定约束。
由于盘的内孔与轴相连接,故在内圆侧面施加z轴方向的固定约束,而在x,y轴方向上施加预定的对应位移,为模拟制动盘的减速运动。
3、盘式制动器温度场-应力场的耦合仿真
本文以首钢SGA3723矿用汽车盘式制动器的结构为例,制动盘的材料为ZG1Cr13,摩擦片材料为树脂基复合材料。计算分析所需参数见表1。总制动时间为3.0s,制动初始车速为25km/h,初始制动压力为10MPa。

表1 材料的特性参数
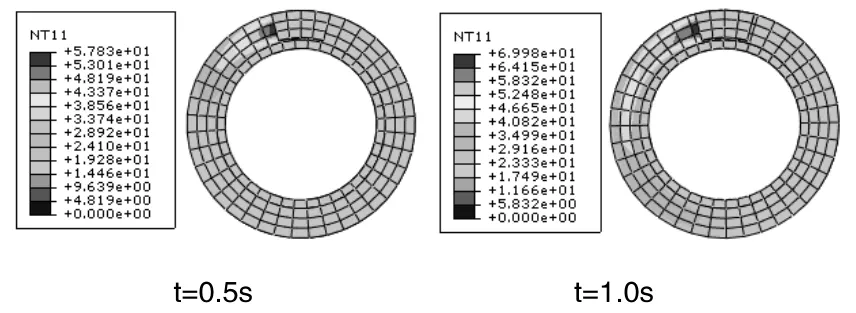

图2 制动不同时刻温度分布

图3 不同半径点温度-时间曲线
图2为制动器持续制动3.0s时制动盘表面温度分布图,在t=2.0s时表面温度达到制动中的最大值,从制动开始制动盘的温度(初始温度为环境温度)一直升高,但温度分布并不均匀。t=3.0s时制动结束,此时温度比t=2.0s时要低一些,主要因为制动后期制动盘的速度很低,此时摩擦产生的热流密度输入量低于制动盘与外界的对流换热量,因此制动盘的温度由最大值开始下降,当到制动结束时制动盘的温度分布接近轴对称分布。图3为不同半径点温度随时间变化曲线,左图最高温度高于右图,这是因为点(1)处的切线速度大于点(2),因此输入的热流密度大,温度比较高。

图4 制动不同时刻应力分布
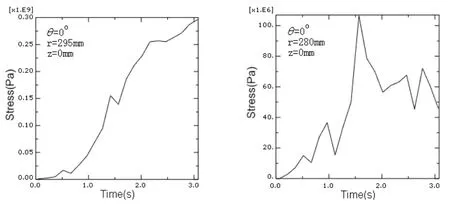
图5 不同半径点应力-时间曲线
从图4和图5可以看出,由盘内温度分布的不均匀引起的热应力分布是相当不均匀的。由于制动时间短,摩擦副产生热量的速度要远高于热量向材料内部传递的热传导速度,制动盘摩擦接触表面温度高于材料内部区域的温度,并且摩擦区域的表面温度要高于非摩擦区域的表面温度,从而在径向、周向产生很大的温度梯度。这一温度梯度使得制动盘摩擦区域部分要向径向和周向膨胀,
但受到非温升的约束而不能自由进行,导致在摩擦高温区域,其径向和周向都产生了很大的压应力。盘的内径处非摩擦区域基本没有什么温升,产生了拉应力。同时制动盘沿半径方向温度变化梯度高于沿轴向的温度变化梯度,从而导致制动盘周向应力明显要高于径向应力。因此,由此而产生的热裂纹往往是沿半径方向分布的。
4、结论
(1)本文建立了盘式制动器温度场-应力场耦合瞬态非轴对称有限元模型及其相关的边界条件,所建模型充分考虑制动器实际尺寸、摩擦热流耦合和移动热源可变效应的影响,能较好的仿真制动器制动过程中的温度场-应力场的动态特性。
(2)温度及应力的最大部位出现在与摩擦片接触的垂直中心部位,在摩擦中这些部位温度及应力不断升高,而制动盘内、外径处温升相对很小,这是因为内、外径距摩擦区相对较远。制动中摩擦片的温度最大值处于摩擦区的出口靠近外径处,这个部位是最容易磨损的部位,这与摩擦片磨损的实际情况相符合。
(3)制动器表面温度随制动开始迅速升高,大约在制动时间三分之二时达到最大值,然后逐渐降低,在制动结束时温度接近轴对称分布。
参考文献
[1]李非雪,张文明,方湄.湿式多片制动器摩擦片温度分布规律[J].北京科技大学学报,2001,23(6):539~542.
[2]王亚幂,李世其,宋少云.多场耦合系统协同设计方法研究[J].机械制造,2006,44(4):34~37.
[3]周凡华,吴光强,沈浩.盘式制动器15次循环制动温度计算[J].汽车工程,2001,23(6):411~413.
[4]刘立忠,刘相华,王国栋.轧制过程的显式动力学有限元模拟[J].东北大学学报,2001,22(3):327~330.
[5]张立军,司扬,余卓平.非均匀盘式制动器热机耦合特性试验研究[J].汽车技术,2008(6):45~49.
Simulation Study of Automobile Disc Brake Based on Dynamic Explicit Finite Element Method
Cheng Lin, Wang Gu’na, Wang Maomei
(Beijing Polytechnic, Beijing 100176)
Abstract:According to the actual geometry of brake disc and the friction plate, the simulation calculation model of three-dimensional transient temperature field and stress field under braking condition is established. Considering the friction characteristics between the brake disc and the friction plate, the dynamic simulation is used to the braking process of disc brake with explicit dynamic module of ABAQUS. The distribution rules of the brake disc transient temperature field and stress field is studied. The temperature field and stress field are coupled. The temperature field and stress field change periodically with braking time.
Keywords:Explicit dynamics; Finite element method; Disk brake; Simulation study
中图分类号:U463.51+2
文献标识码:A
文章编号:1671-7988(2016)05-09-04
作者简介:成林,博士研究生,就职于北京电子科技职业学院汽车工程学院。主要研究方向为汽车制动系统的优化设计与仿真。

