随机选择变异及自适应差分进化算法的研究

郭义波, 程际云, 李　芹, 杨　平

(1.上海电力学院, 上海　200090; 2.上海明华电力技术工程有限公司, 上海　200437)



随机选择变异及自适应差分进化算法的研究

郭义波1, 程际云2, 李芹1, 杨平1

(1.上海电力学院, 上海200090; 2.上海明华电力技术工程有限公司, 上海200437)

摘要:为兼顾搜索速度和精度,提高搜索效率,克服不易跳出局部最优的缺点,提出了随机选择变异策略、自适应调整变异率和自适应调整交叉率3种改进设想.利用3种改进设想改进DE算法,得到了7种改进算法,将7种改进算法应用到双容水箱液位模型闭环辨识案例中.结果表明,7种改进算法都提高了跳出局部最优的能力,综合比较可知,3种改进设想同时应用的改进算法性能最优.

关键词：差分进化算法; 随机选择变异; 自适应调整; 闭环辨识

差分进化算法(Differential Evolution,DE)是基于群体智能的优化算法,它保留了基于种群的全局搜索策略,其特有的记忆功能使其能够动态跟踪搜索情况,从而调整搜索策略,具有较强的全局搜索能力和鲁棒性[1].凭借算法参数少、搜索能力强、算法简单等特点,差分进化算法在多目标路径规划[2]、梯级水库调度优化[3]、PID优化[4]、模型参数辨识[5-6]等方面得到了广泛的应用.然而与其他智能优化算法相类似,差分进化算法也存在局部最优、收敛精度不高及收敛速度慢等问题.为此,对基本差分进化算法进行了改进研究.文献[7]提出了一种依据种群中个体的分布情况来调整算法参数的自适应差分进化算法,应用于模型参数辨识中,结果优于遗传算法及基本差分进化算法.文献[8]针对常用变异策略DE/rand/1和DE/best/1的缺点提出了一种新的变异策略,为了平衡全局搜索与局部搜索能力采用自适应变异因子,辨识精度及速度优于其他两种改进算法及基本差分进化算法.文献[9]提出了一种利用模糊逻辑来调整变异因子的自适应差分进化算法,仿真结果表明改进是可行的.文献[10]引入一个新的变异参数,根据算法的搜索情况自适应调整变异率,将改进算法应用于非线性系统模型参数的辨识中,性能较优.

为了平衡算法搜索速度和搜索精度,本文综合两种变异策略(DE/best/1和DE/rand/1)的优点,提出了随机选择变异策略的改进设想;为了提高算法搜索的效率,根据文献[11]中对自适应调整变异率和自适应调整交叉率的理论描述,应用新公式对交叉率和变异率进行调整,从而提出了新型自适应调整变异率和自适应调整交叉率的改进设想.利用3种改进设想的多种组合来改进基本算法得到7种改进算法,并将7种改进DE算法应用在双容水箱液位模型辨识案例中进行性能验证.结果表明,7种改进DE算法跳出局部最优的能力都高于基本算法.综合考虑跳出局部最优能力、时耗、快速性3项性能,3种改进设想同时应用的改进算法性能最优.

1差分进化算法

差分进化算法的思想是在父代种群中任意选取两个或多个个体进行差分操作,并以一定的变异率进行放缩,然后与种群中另一个个体相加得到变异个体,变异个体与父个体以一定的交叉率进行交叉,得到试验个体,比较试验个体与父个体的适应度值,选择较优的个体保存在下一代种群中.当满足终止条件时,结束搜索,输出最优个体.首先,DE算法在问题的解空间内生成一组随机个体形成初始种群,然后通过变异、交叉、选择操作,产生下一代种群.

1.1变异

变异操作就是从父代个体中任意选取两个或多个父代个体进行差分操作,再按一定的变异率进行放缩,然后与另一个父代个体进行相加得到变异向量.变异交叉策略的命名一般约定为DE/x/y/z形式,其中x表示从父代种群中选取的基向量的形式,y表示差分向量的个数,z表示采用的交叉方式.PRICE和STORN提出了以下5种变异策略[11].

DE/rand/1:

(1)

DE/best/1:

(2)

DE/rand-to-best/1:

vi,g=xr1,g+F(xbest,g-xr1,g)+F(xr2,g-xr3,g)

(3)

DE/rand/2:

vi,g=xr1,g+F(xr2,g-xr3,g)+F(xr4,g-xr5,g)

(4)

DE/best/2:

vi,g=xbest,g+F(xr1,g-xr2,g)+F(xr3,g-xr4,g)

(5)

式中:xbest,g——当前种群中最优个体;

xr1,g,xr2,g,xr3,g,xr4,g,xr5,g——当前种群中任意选取的互不相同的个体；

i,r1,r2,r3,r4,r5——个体编号;

g——代数;

vi,g——得到的变异向量;

F——变异率.

上述5种变异策略中，DE/rand/1与DE/best/1使用较为广泛.

1.2交叉

由变异操作得到的变异向量与父个体进行交叉操作,目的是使交叉后的试验向量拥有父个体和变异向量的信息,保留父个体优良特性的同时又增加了种群的多样性.DE算法有指数交叉(用exp表示)和二项式交叉(用bin表示)两种交叉方式.

指数交叉操作方式为:

(6)

式中：ui,j,g——试验向量;

vi,j,g——变异向量;

xi,j,g——父个体;

i——个体编号;

g——代数;

j——个体分量编号;

(l)C——取大于l的最小整数,l是零与个体向量维数D之间的随机数;

L——整数,在1与D之间.

指数交叉的具体操作是,首先在0与D之间选取一个随机数,并进行取整作为交叉的起点,起点处的试验向量分量取自变异向量,自起点后根据随机数与交叉率(CR)的比较结果选取一个整数L作为取自变异向量分量的长度,试验向量的其他分量都取自父个体.

二项式交叉操作方式为:

(7)

式中:jrand——[1,D]内的随机整数,j=1,2,3,…,D.

二项式交叉的具体操作是,由试验向量的第一个分量开始,根据随机数与交叉率CR的比较结果决定试验向量分量是取自变异向量还是父个体,如果随机数小于或者等于CR,则取自变异向量,否则,取自父个体,同时,保证每个试验向量至少有一个分量取自变异向量.二进制交叉操作在DE算法中使用较为广泛.

1.3选择

DE采用“贪婪”策略进行选择,比较父个体xi,g与试验向量ui,g的适应度值f(·)来决定最优个体;对于求取最小值问题,选择操作方式为:

(8)

式中:xi,g+1——下一代个体.

2差分进化算法的改进设想

2.1随机选择变异策略

5种变异策略与2种交叉策略相结合,共可以得到10种变异交叉策略:DE/best/1/bin,DE/rand/1/bin,DE/rand-to-best/1/bin,DE/rand/2/bin,DE/best/2/bin,其中常用是DE/best/1/bin和DE/rand/1/bin.变异策略DE/best/1以当前种群中最优个体为基向量,随着进化的进行,变异操作使种群中的个体趋向于最优个体附近,算法收敛速度快.缺点是对于存在局部最优解的问题,收敛容易陷入局部最优.变异策略DE/rand/1以当前种群中随机个体为基向量,有利于保持种群的多样性,加大了搜索到最优个体的概率,缺点是算法收敛速度太慢或者搜索不到最优解.为了综合两种变异策略的优点,本文提出了一种随机选取两种变异策略的改进设想,引入选择因子C,在进行变异操作前,首先比较随机数与选择因子C,根据比较情况选择两种变异策略中的一种.即:

(9)

2.2自适应调整变异率

变异率F的作用是对差分向量进行放缩,生成变异向量.如果基向量的适应度值较优,则希望变异向量中包含较多的基向量成分,故此时需要较小的F对差分向量进行较小的放缩,使算法在基向量附近搜索,易于找到较优解;当基向量的适应度较差时,则希望变异向量中包含较少的基向量成分,故此时需要较大的F,对差分向量进行较大的放缩,使搜索范围扩大,能够探索到较大解空间,增加搜索到最优解的概率.因此,可以根据基向量的适应度值合理地自适应调整变异率F,基向量的适应度越优,变异率F就越小.对于求取最小值问题,调整策略为:

(10)

式中:Fmin,Fmax——变异率的下限与上限;

fmin,fmax——当前种群中个体的最小适应度值与最大适应度值;

i——个体编号;

fi——基向量的适应度值.

2.3自适应调整交叉率

交叉率CR决定了试验向量中包含变异向量成分的多少.如果变异向量的适应度值较优,则试验向量中应包含较多的变异向量成分,交叉率CR的选取也应较大.当变异向量的适应度值较差时,则试验向量应包含较少的变异向量成分,交叉率CR的选取也应较小.根据以上分析,对于求取最小值问题,调整策略为:

(11)

式中:CRmin,CRmax——交叉率的下限与上限;

fi——变异向量的适应度值.

2.47种改进算法

利用3种改进设想分别应用于DE算法得到改进算法1,算法2,算法3;利用3种改进设想两两结合应用于DE算法,可得到改进算法4,算法5,算法6;利用3种改进设想同时应用于DE算法可得到改进算法7.具体如表1所示.

表1　7种改进算法

37种改进算法在闭环辨识案例中的应用及性能分析

3.1双容水箱液位模型

设双容水箱液位模型的传递函数形式为:

(12)

该模型中共有4个待辨识参数K,T1,T2,τ,由于4个参数相互影响,利用基本DE算法进行辨识时,往往因陷入局部最优使参数T1和T2的辨识结果不够准确.

3.2闭环辨识困难及应用智能优化算法的需求

闭环辨识比开环辨识更困难一些.用传统的最小二乘方法不可能辨识的闭环辨识问题,用现代的智能优化算法就有了可行解,但其对智能优化算法也提出了更高的要求.因此,改进DE算法用于闭环辨识验证具有一定的现实意义.

3.37种改进算法的闭环辨识案例验证试验

由双容水箱试验装置获取闭环状态下双容水箱液位试验数据,包括上水阀开度数据及下水箱液位数据,采样周期取1 s,数据长度为900,其采集点位置如图1所示.上水阀开度曲线及下水箱液位曲线如图2和图3所示.

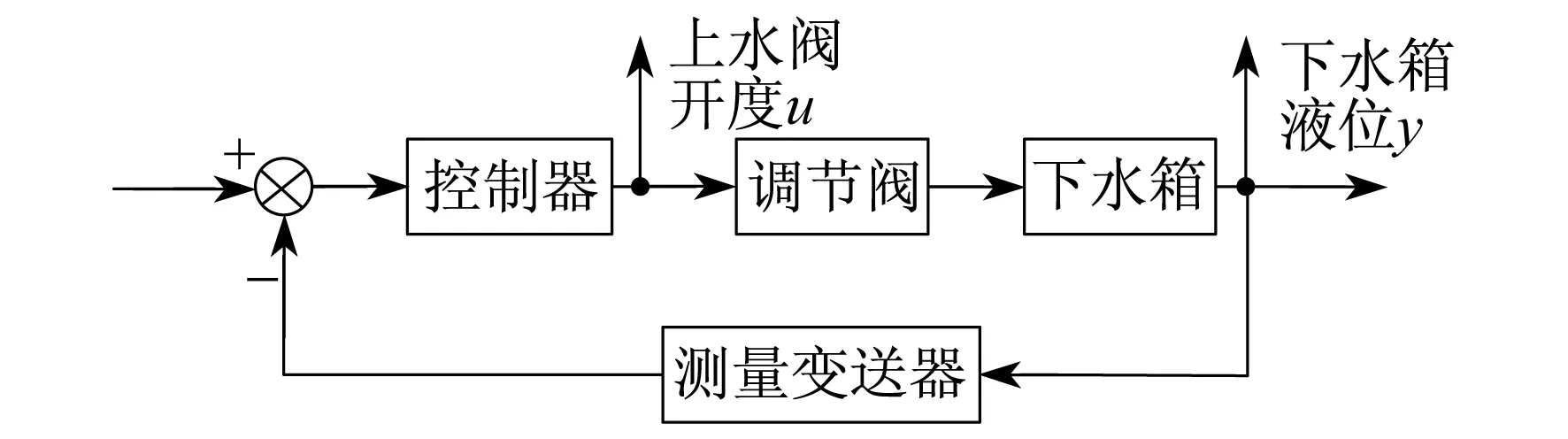
图1　水箱液位控制系统框示意

图2　上水阀开度曲线

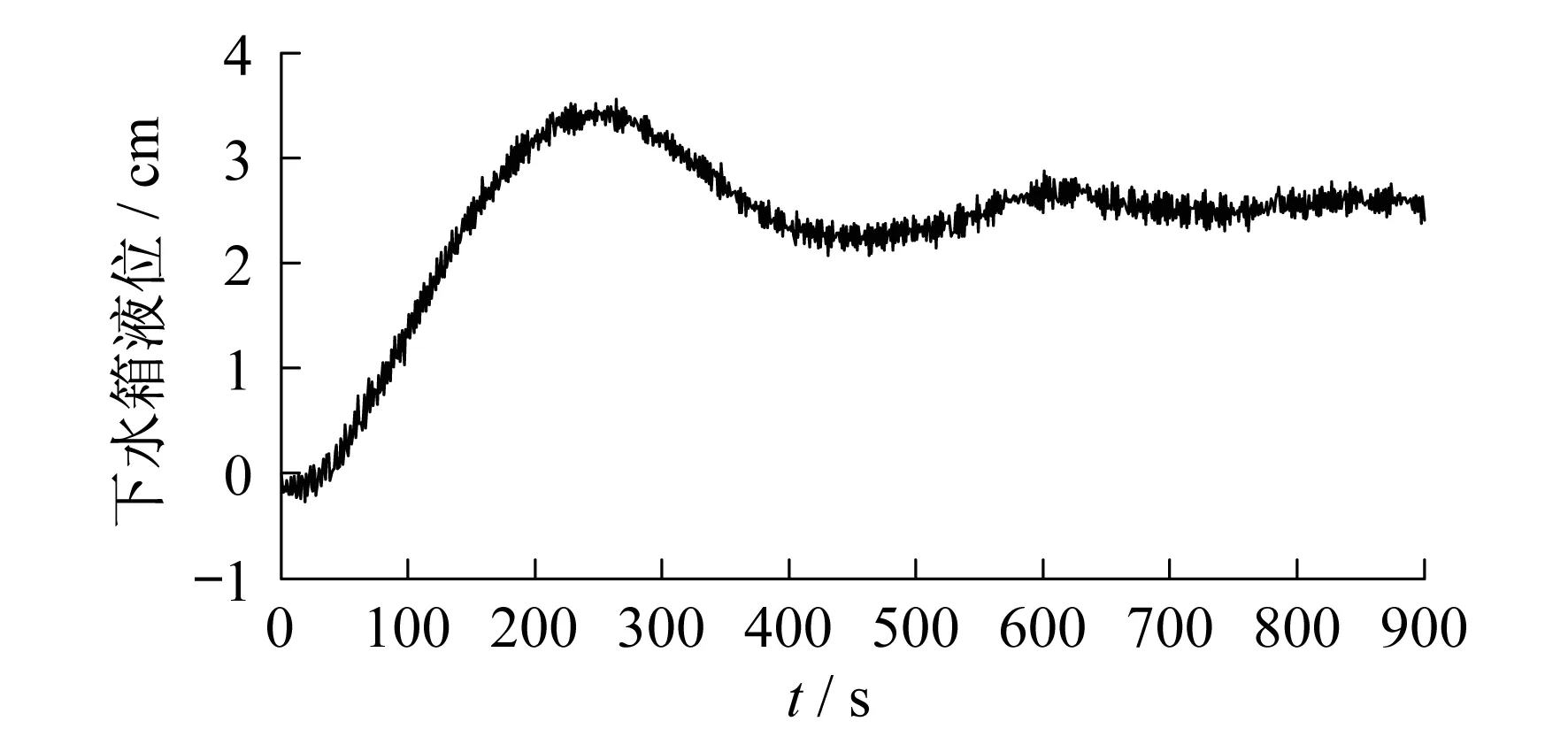
图3　下水箱液位曲线

分别采用基本差分进化算法(DE/best/1/bin)和以上7种改进算法在Matlab环境下辨识出双容水箱液位模型中K,T1,T2,τ这4个参数.在辨识计算中所用的算法参数F的范围取[0.3,0.6],CR的范围取[0.6,0.9][1];选择因子取0.6.具体设置如表2所示.4个参数的搜索范围取[0.000 1 100],[0.000 1 500],[0.000 1 500],[0.000 1 100];种群规模数取待辨识参数个数的10倍(即40);最大迭代次数取100.适应度函数及辨识误差函数为:

(13)

式中:n——数据长度;

yi——第i个待辨识数据;

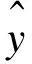
表2　算法的参数设置

3.47种算法的应用性能分析

为了分析不同算法的性能,记录20次辨识计算中陷入局部最优的次数、仿真时耗、误差降至10所需迭代次数,得到的结果如表3所示.

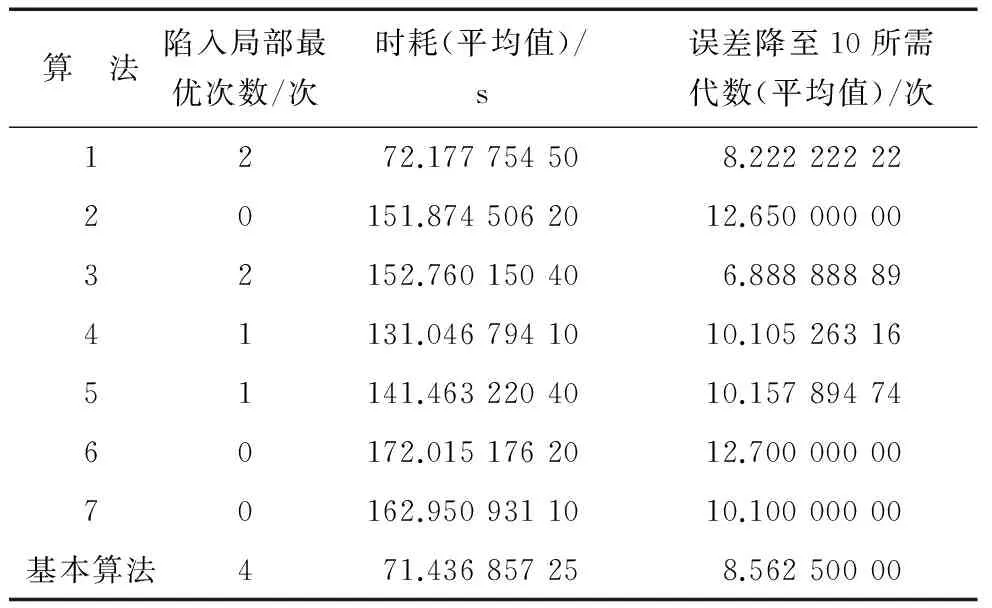
表3　20次辨识结果

由表3可知.局部最优辨识结果为K=1.024 8,T1=236.390 9,T2=56.898 3,τ=21.233 6,辨识误差为11.533 8.最优辨识结果为K=1.062 5,T1=291.769 8,T2=0.000 1,τ=61.231 7,辨识误差为5.427 4.则最优辨识结果及局部最优辨识结果的传递函数模型分别为:

(14)

(15)

利用Simulink仿真平台,可得到最优模型和局部最优模型在实际的上水阀门开度数据输入下的响应曲线,与实际的液位曲线对比结果如图4所示.

由图4可知,最优模型响应曲线与实际液位曲线吻合较好,说明最优模型的传递函数能够反映实际对象的特性,而局部最优模型响应曲线与实际液位曲线相差明显.局部最优模型的时延参数τ=61.231 7,局部最优模型响应曲线与实际液位曲线相比,时延明显偏大.究其原因可知,由于纯延迟后的一段时间内实际液位值与零非常接近,对适应度影响较小,其在整个适应度值中所占的比重也较小,容易被忽略,从而造成时延参数辨识不准[12].

图4　实际曲线与辨识结果仿真曲线对比

由表3可知,7种改进算法陷入局部最优的次数都少于基本算法,说明改进算法提高了跳出局部最优的能力.从时耗数据来看,算法1在7种改进算法中平均用时最少;从误差降到10所需代数(即快速性)来看,算法3所需代数最少;从陷入局部最优的次数来看,算法6和算法7在20次辨识中都没有陷入局部最优.

分析表明,算法1只进行了随机选择变异策略的改进,而算法2至算法7都进行了自适应调整算法参数的改进,自适应调整算法参数的改进都需要计算粒子的适应度信息,并以此信息计算每代的变异率和交叉率,这必将增大每次迭代的计算量,从而增加总体搜索时耗.因此,除算法1与基本算法时耗较接近外,其他改进算法的平均时耗都要大大超过基本算法.

算法3只进行了自适应调整交叉率的改进,自适应调整交叉率提高了算法的搜索效率;同时,由于变异策略选用的是与基本算法类似的DE/best/1策略,其优点就是搜索快速,因此算法3表现出优于其他算法的快速性.

算法6是对两个算法参数同时进行自适应调整,对变异率进行自适应调整采用的是DE/rand/1变异策略,这增加了种群的多样性,从而增大了跳出局部极值点的能力.算法7是3种改进方案相结合的改进算法,随机选择变异策略综合了DE/rand/1和DE/best/1的优点,即增加了种群的多样性,又提高了搜索的快速性.由于算法7在部分代中采用了DE/rand/1变异策略,减少了计算变异率的次数,导致算法7的时耗及快速性都要优于算法6.

在跳出局部极值点能力、时耗、快速性3个指标中,最重要的指标是跳出局部极值点的能力,它是辨识成败与否的关键.因此,综合考虑,算法7的性能最优.

4结语

将3种改进设想,随机选择变异策略、自适应调整变异率和自适应调整交叉率组合应用于基本DE算法,提出了7种改进算法并应用于双容水箱液位模型闭环辨识案例中进行性能验证.对比基本DE算法辨识结果表明,7种算法跳出局部最优的能力都得到了提高;综合跳出局部最优能力、时耗、快速性3项性能表明,3种改进设想同时应用的改进算法性能最优.

参考文献：

[1]刘金琨,沈晓蓉,赵龙.系统辨识理论及MATLAB仿真[M].北京:电子工业出版社,2013:32-58.

[2]裴振奎,刘真,赵艳丽.差分进化算法在多目标路径规划中的应用[J].辽宁工程技术大学学报:自然科学版,2010,29(5):899-902.

[3]郑慧涛,梅亚东,胡挺,等.改进差分进化算法在梯级水库优化调度中的应用[J].武汉大学学报:工学版,2013 (1):57-61.

[4]常俊林,李亚朋,马小平,等.基于改进差分进化算法的PID优化设计[J].控制工程,2010,17(6):807-810.

[5]许津津,马进,唐永红,等.基于改进DE算法的负荷建模参数辨识[J].电力系统保护与控制,2009,37(24):36-40.

[6]薛晓岑,向文国,吕剑虹.基于差分进化与 RBF 神经网络的热工过程辨识[J].东南大学学报:自然科学版,2014,44(4):769-774.

[7]陶国正.基于改进微分进化算法的过程模型参数辨识[J].电气应用,2011(4):40-44..

[8]唐德翠,邓晓燕,朱学峰,等.改进差分进化算法辨识加药凝絮过程参数[J].控制工程,2010(4):80-82.

[9]任甜甜,张宏立.基于改进差分进化算法的非线性系统辨识[J].计算机仿真,2014,31(7):342-345.

[10]熊伟丽,陈敏芳,张乾,等.基于改进差分进化算法的非线性系统模型参数辨识[J].计算机应用研究,2014,31(1):124-127.

[11]张美春.差分进化算法与应用[M].北京:北京理工大学出版社,2014:10-11.

[12]张洪涛,胡红丽,徐欣航,等.基于粒子群算法的火电厂热工过程模型辨识[J].热力发电,2010,39(1):59-61.

(编辑胡小萍)

Research on Random Selection Mutation and Adaptive Differential Evolution Algorithm

GUO Yibo1, CHENG Jiyun2, LI Qin1, YANG Ping1

(1.ShanghaiUniversityofElectricPower,Shanghai200090,China; 2.ShanghaiMingHuaElectricPowerTechnologyEngineeringCo.,Ltd.,Shanghai200437,China)

Abstract:In order to take into account search speed and search accuracy,improve search efficiency,overcome the shortcoming which does not easily escape from local optimum value,three improved assumptions are proposed,namely,random selection mutation strategy,adaptive adjustment of mutation rate and adaptive adjustment of crossover rate.Three kinds of improved assumptions are used to improve the basic algorithm and get seven kinds of improved algorithms,which are applied to two-tank water level model closed-loop identification case.Case verification shows that seven kinds of improved algorithms increase the ability to jump out of local optimum value.Comprehensive comparison shows that the performance of improved algorithm where three improved assumptions are applied simultaneously is the best.

Key words:differential evolution algorithm; random selection mutation; adaptive adjustment; closed-loop identification

DOI：10.3969/j.issn.1006-4729.2016.02.012

收稿日期：2015-07-22

作者简介：通讯郭义波(1990-),男,在读硕士,河南商丘人.主要研究方向为热工过程模型辨识.E-mail:913672133@qq.com.

基金项目：上海市电站自动化技术重点实验室项目(13DZ2273800); 上海市科技创新行动计划(13111104300).

中图分类号：TP181

文献标志码：A

文章编号：1006-4729(2016)02-0162-05