基于小波奇异熵的电力系统振荡中对称故障的识别算法

肖贤贵, 高　亮, 屠友强, 刘天明

(1.上海电力学院 电气工程学院, 上海　200090; 2.上海申能临港燃机发电有限公司 运行部, 上海　201306)



基于小波奇异熵的电力系统振荡中对称故障的识别算法

肖贤贵1, 高亮1, 屠友强2, 刘天明1

(1.上海电力学院 电气工程学院, 上海200090; 2.上海申能临港燃机发电有限公司 运行部, 上海201306)

摘要:运用小波分析处理各相故障电流波形,并求各相电流的小波奇异熵的算法,与设定的阈值比较大小以判定是否为故障.在Matlab/Simulink下建立了一个电力系统模型,分别考虑了合闸时刻、过渡电阻、接地距离、振荡频率、噪声等多种因素后,做了大量仿真分析.得出了该算法鲁棒性好,具有干扰因素影响的特点.

关键词：小波奇异熵; 电力系统振荡; 对称故障

当电力系统发生对称和不对称故障时,测量阻抗落在距离保护动作区域内,此时距离保护应当可靠动作.当电力系统处于振荡状态时,测量阻抗不再是固定值,而是周期性变化的.此时,测量阻抗可能进入距离保护动作区域内,进而导致保护误动作.所以,准确鉴别电力系统故障和振荡,对于电力系统安全有着十分重要的意义.

目前的振荡闭锁措施主要可以分为3类.一是检测电流的零序或负序分量[1],但是该方法的缺点是仅适用于非对称故障,不适用于对称故障.在发生三相对称故障时,零序分量和负序分量均为零.二是检测某一个电气参数的变化率[2-5].文献[2]提出利用测量有功功率和无功功率的变化率来鉴别电力系统振荡;文献[3]提出利用测量电力系统振荡中心的电压幅值变化率来判定电力系统振荡,但这两种算法的关键在于判定阈值的选取.不同的系统,判定阈值一般不同,阈值的选取依赖于工作人员的经验.文献[4]和文献[5]提出了测量保护安装处的电压相角变化率的算法,但是该文献仅仿真了单相接地故障的情况,并未指出该算法是否适用于对称故障.三是基于数学工具的算法[6-10].文献[6]至文献[8]提出用小波分析处理故障后暂态电流的方法,该算法的缺点在于小波分析对噪声十分敏感,且该文献未给出滤波算法.文献[9]提出运用S变换和概率神经网络的算法,该方法的优点是S变换结合了小波分析和快速傅立叶变换的优点,而且对噪声不敏感.但该算法的不足在于鉴别准确率仅为90%.文献[10]提出了模糊神经网络算法,该算法的不足之处是需要大量的样本进行训练,而且存在着过度训练的可能.文献[11]提出根据三相有功的突变情况来检测故障,但是没有说明该算法的抗噪声能力.文献[12]设计了一个暂态观测器的算法,但并未讨论该算法对干扰因素的适应性.

本文在上述基础上提出了一种基于小波奇异熵[13-15]来识别振荡和故障的算法.其基本原理是:对暂态电流做小波变换得到不同尺度下的小波系数,进而构成一个时频矩阵.在对称故障情况下,暂态电流的幅值大于振荡状态下的幅值.因此,对故障暂态电流做小波分析,对应的小波奇异熵也不同.基于这个原理能够准确识别电力系统振荡和对称故障状态.最后,对某500 kV线路进行仿真,验证了该算法的可行性.

1小波奇异熵的原理

1.1小波分析基本理论

对某个一维连续时间信号x(t)的连续小波变换定义式为:

(1)

式中:a——与频率对应的尺度参数,a>0;

b——与时间对应的位移参数;

ψa,b(t)——基于小波平移和伸缩生成的一组小波基.

由于小波分析的结果依赖于小波基函数,Daubechies小波具有正交、紧支的特点,本文选db5小波对信号进行分解.

对某个信号做小波分析,得到一系列的时间-频率相关的小波系数,这些系数构成一个m×n阶的矩阵.由矩阵奇异值分解可知,对于任何一个m×n阶的矩阵D,都可以分解为:

(2)

式中:U——m×l维的矩阵;

V——l×n维的矩阵;

Λ为对角矩阵,主对角线元素为λi(i=1,2,3,…,l)是非负的,并且按降序排列,这些主对角线元素是小波分析结果矩阵D的奇异值.

1.2信息熵理论

信息熵理论指出,若某个不确定的系统可以用有限个随机变量X表示其状态特征,其中状态特征xi的概率为P(xi)=Pi,i=1,2,3,…,N.且0≤Pi≤1,∑Pi=1.xi所包含的不确定信息量称为自信息量,表示为:

(3)

于是X的信息熵公式为:

(4)

根据小波分析和信息熵理论,得到小波奇异熵[13](Wavelet Singular Entropy,WSE)公式为:

(5)

(6)

式中:Δpi——第i阶增量小波的奇异熵.

目前,小波奇异熵在电力系统中已应用于如暂态信号分析[13]、变压器故障检测[14]、IGBT模块的故障检测[15]等.

2算例仿真

为了验证本文所提出的算法的有效性,在Matalb/Simulink中建立模型,模型如图1所示.

图1　仿真系统模型

为了尽可能接近实际情况,该模型采用了某500 kV线路的参数,线路总长340 km.考虑到线路的对地分布电容,线路模型采用10个π型等值电路串联.线路的参数如下：正序电抗X1=0.278 3 Ω/km,零序电抗X0=0.649 4 Ω/km,正

序电阻R1=0.027 Ω/km,零序电阻R0=0.194 8 Ω/km,正序电容C1=0.012 7 μF/km,零序电容C0=0.009 μF/km,系统正序阻抗Zm1=Zn1=2.21+j25.04 Ω,零序阻抗Zm0=Zn0=4.90+j31.51 Ω.

正常情况下,双侧电源的电力系统和两侧发电机的频率均为50 Hz,相角差δ为固定值,此时系统稳定运行.如果因为某些原因,一侧的发电机失去同步,电力系统发生振荡,测量阻抗可能会进入动作区域导致误动,因此鉴别系统振荡和振荡再故障十分重要.为了模拟系统振荡再故障时的波形,设置如下故障:两侧频率差为0.5 Hz,对称故障为0.02 s时刻发生,接地电阻为5 Ω,故障持续到0.1 s时刻切除.故障状态下的A相电流和振荡状态下的A相电流如图2所示.

图2　电力系统振荡状态和故障状态的电流波形

由图2可以看出,在0.02 s至0.1 s时刻,系统发生对称故障，故障电流的瞬时峰值达到3 000 A以上,而振荡状态下的电流峰值不超过1 000 A.根据前面的论述,故障状态下的电流对应的小波奇异熵应大于振荡状态下的电流的小波奇异熵,由此可以区分对称故障和振荡状态.在此基础上给出了本算法的流程图,如图3所示.

分别取故障时刻发生后一个周期的波形和振荡状态下一个周期的波形进行分析,两种电流波形在各细分尺度下(d1～d6)随时间的变化分别如图4和图5所示.

利用式(4)和式(5)计算振荡再故障和振荡状态的三相电流小波奇异熵.不同状态下的三相电流对应的小波奇异熵如表1所示.表1中,A相电流WSE表示A相电流对应的小波奇异熵,其他类似；各相电流小波奇异熵为无单位的数值.

由表1可以得出,纯振荡的三相电流的小波奇异熵的绝对值远小于振荡再故障对应的小波奇异熵的绝对值.由此可以得出判据:当三相电流的小波奇异熵的绝对值之和大于某个阈值时,判定为振荡状态故障,保护器动作;当三相电流的小波奇异熵的绝对值之和小于某个阈值时,判定为电力系统发生纯振荡,保护器不动作.经过多次仿真试验后,该阈值设定为1.8e+5.

图3　算法流程示意

图4　故障暂态电流波形的各尺度小波系数

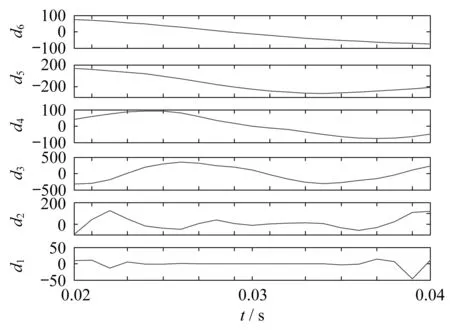
图5　振荡电流波形的各尺度小波系数

状 态A相电流WSEB相电流WSEC相电流WSE振荡时故障-1.1127e+005-9.7361e+004-1.1564e+005纯振荡 -3.4010e+004-2.5989e+004-4.0759e+004

3多种干扰因素的影响分析

在实际情况中,电力系统中存在故障的合闸角、过渡电阻、接地距离、振荡频率等多种干扰因素,为了验证本文提出的算法能否克服干扰因素的影响,对这些因素分别进行讨论.

3.1不同相角差的影响分析

振荡时,系统两侧的相角差在0～360°之间变化,因此故障发生时两侧电源的相角差不同.为了考察本文算法能否克服不同合闸角的影响,故障设置在0.02 s时刻发生,过渡电阻5 Ω,接地点到M端距离为170 km,振荡频率为0.5 Hz,故障时刻以每45°为一个间隔,到180°.三相电流的小波奇异熵如表2所示.

表2　不同相角差的三相电流的小波奇异熵

由表2得知,当相角差在0～180°之间变化时,三相电流的小波奇异熵总和的绝对值均大于1.8e+5,可判定为对称故障状态.

3.2过渡电阻的影响分析

在电力系统发生故障时,故障处通常会有过渡电阻.

为了分析本文的算法是否能够克服过渡电阻的影响,故障设置为:发生时刻0.02 s,接地点到M端距离170 km,振荡频率为0.5 Hz.在不同的过渡电阻条件下,三相电流的小波奇异熵如表3所示.

表3　过渡电阻变化下的三相电流的小波奇异熵

由表3得知,随着过渡电阻由5 Ω依次增大至50 Ω,三相电流的小波奇异熵之和有所下降,这是由于过渡电阻增大,三相电流幅值会减小,对应的小波奇异熵绝对值也会减小,但均大于阈值1.8e+5,均可准确判定为对称故障状态.

3.3接地距离的影响分析

被研究的线路全长340 km,为了分析接地距离对本文算法的影响,将故障设置在线路的不同位置.故障发生时刻0.04 s,过渡电阻为5 Ω,振荡频率为0.5 Hz,接地点与M端的距离占线路全程的10%～90%.在不同的接地距离情况下,三相电流的小波奇异熵计算结果如表4所示.

由表4可知,接地点与M端的距离占线路全长的比例依次从10%增长到90%,三相电流的小波奇异熵均大于阈值1.8e+5,均判定为对称故障状态.计算结果表明，本文算法受接地距离变化的影响较小.

表4　接地距离变化下的三相电流的小波奇异熵

3.4振荡频率变化的影响分析

电力系统发生振荡时,大多数情况下能够通过自动装置回复同步,而且当发电机频率偏移到一定程度时(一般频率偏移不超过1.5 Hz)时,发电机保护会自动切机.因此本文的振荡频率最高设置为1.5 Hz.故障设置了不同的振荡频率,故障时刻0.04 s,过渡电阻为5 Ω,接地点距离M端170 km,振荡频率为0.5～1.5 Hz.在不同振荡频率下,三相电流的小波奇异熵计算结果如表5所示.

表5　不同振荡频率下的三相电流小波奇异熵

由表5可以得出,振荡频率在0.5～1.5 Hz变化时,三相电流的小波奇异熵均大于阈值1.8e+5,均判定为对称故障状态.结果证明了本文的算法不受振荡频率的影响.

3.5噪声的影响分析

以上情况都是在软件中模拟得到的,但实际情况中采样信号通常伴随着噪声,这些噪声可能对结果造成影响.为了考察该算法的抗噪声能力,设置故障为振荡频率1 Hz,过渡电阻5 Ω,接地点距离M端170 km,故障发生时刻0.04 s,对三相故障电流加入信噪比为30 dB的白噪声并进行滤波,其各相WSE如表6所示.

由表6可以得出,三相电流的小波奇异熵均大于阈值1.8e+5,判定为故障状态,结果说明该算法具有较好的抗噪声干扰的能力.

表6　叠加30 dB的白噪声后的三相电流小波奇异熵

4结语

本文在现有文献的基础上,提出了一种新的鉴别电力系统振荡再故障和纯振荡的算法.经过对某500 kV线路大量的仿真验证,计算结果表明该算法不受合闸时刻、过渡电阻、接地点、振荡频率、噪声等干扰因素的影响,具有良好的适应性,为距离保护的闭锁提供了一种新的判定方法.

参考文献：

[1]张保会,尹项根.电力系统继电保护[M].第2版.北京:中国电力出版社,2010:102-103.

[2]LIN X,GAO Y,LIU P.A novel scheme to identify symmetrical faults occurring during power swings[J].IEEE Transactions on Power Delivery,2008,21(1):73-81.

[3]NAYAK P,BAJPAI P.A fault detection technique for the series compensated lineduring power swings[J].IEEE Transactions on Power Delivery,2013,28(2):1 836-1 841.

[4]MECHRAOUI A,THOMAS D W P.A new blocking principle with phase and earth fault detection during fast power swings for distance protection[J].IEEE Transactions on Power Delivery,1995,10(3):1 242-1 248.

[5]MECHRAOUI A,THOMAS D W P.A new principle for high resistance earth fault detection during fast power swings for distance protection[J].IEEE Transactions on Power Delivery,1997,12(4):1 452-1 457.

[6]BRAHMA S M.Distance relay with out-of-step blocking function using wavelet transform[J].IEEE Transactions on Power Delivery,2007,22(3):1 360-1 366.

[7]FAIZ J,LOTFI Fard S.A novel wavelet-based algorithm for discrimination of internal faults from magnetizing inrush currents in power transformers[J].IEEE Transactions on Power Delivery,2006,21(4):1 989-1 996.

[8]ZHANG N,KEZUNOVIC M.Transmission line boundary protection using wavelet transform and neural network[J].IEEE Transactions on Power Delivery,2007,21(4):859-869.

[9]MORAVEJ Z.An effective combined method for symmetrical faults identification during power swing[J].Electrical Power and Energy Systems,2015,64(1):24-34.

[10]ZADEJ H K,LI Z.A novel power swing blocking scheme using adaptive neuro-fuzzy inference system[J].Electrical Power System Research,2008,78(7):1 138-1 146.

[11]MAHAMEDI B,ZHU J.A novel approach to detect symmetrical faults occurring during power swings by using frequency components of instantaneous three-phase active power[J].IEEE Transactions on Power Delivery,2012,27(3):1 368-1 376.

[12]KHODAPARAST J,KHEDERZADEH M.Three-phase fault detection during power swings by transient monitor[J].IEEE Transactions on Power Systen,2015,30(5):2 558-2 564.

[13]符玲,何正友,麦瑞坤,等.小波熵证据的信息融合在电力系统故障诊断中的应用[J].中国电机工程学报,2005,28(13):64-69.

[14]沈刚,周雒维,杜雄,等.基于小波奇异熵理论的IGBT模块键和线脱落故障特征分析[J].中国电机工程学报,2013,28(6):165-171.

[15]王冰,刁鸣,宋凯.基于小波奇异熵和相关向量机的氢气传感器故障诊断[J].电机与控制学报,2015,19(1):96-101.

(编辑白林雪)

A Novel Approach to Detect Symmetrical Faults During Power Swing by Wavelet Singularity Entropy

XIAO Xiangui1, GAO Liang1, TU Youqiang2, LIU Tianming1

(1.School of Electrical Engineering, Shanghai University of Electrical Power, Shanghai200090, China;2.Operation Dept., Shanghai Shenneng Lingang CCGT Power Generation Co., Ltd., Shanghai201306, China)

Abstract:A novel algorithm is presented based on wavelet singularity entropy to analyze the current wave after fault occurring.Then each phase current wave is computed.A simulation model is built and simulated in MATLAB/SIMULINK environment.Besides,interference factors such as inception time,ground resistance,fault location,slip frequency and noise are also discussed comprehensively.It is concluded that the algorithm is immune to interference factors and the proposed scheme is robust.

Key words:wavelet singularity entropy; power swing; symmetrical fault

DOI：10.3969/j.issn.1006-4729.2016.02.011

收稿日期：2015-10-14

作者简介：通讯肖贤贵,(1988-),男,在读硕士,湖北仙桃人.主要研究方向为电力系统继电保护.E-mail:634881135@qq.com.

基金项目：上海绿色能源并网工程研究中心资助项目(13DZ2251900).

中图分类号：TM711.2

文献标志码：A

文章编号：1006-4729(2016)02-0156-06