一类广义KdVKS方程初值问题的不适定性

王宏伟，尚蒙娟，徐国雄

(安阳师范学院 数学与统计学院，河南 安阳 455000)



一类广义KdVKS方程初值问题的不适定性

王宏伟，尚蒙娟，徐国雄

(安阳师范学院 数学与统计学院，河南 安阳 455000)

[摘要]研究了一类广义KdVKS方向的初值问题. 通过构造合适的初值， 在Sobolev空间Hs(R)(s<-1)中证明了这类方程的解映射不是C3的， 得到了这类初值问题的不适定性.

[关键词]初值问题;KdVKS方程;不适定性

1引言

本文研究如下一类具有立方非线性项的KdVKS方程的初值问题:

(1)

其中u=u(x，t)是未知函数. 方程(1)是很多物理问题的数学模型， 如它可以描述斜面上粘性流体长波流[1]和等离子体中的漂移波[2].

如果方程(1)的解是存在唯一的， 并且解映射是光滑的， 则称方程(1)是适定的. 如果其中至少有一个条件不成立， 就称方程是不适定的.Biagioni[3]在非线性项是(ux)2和uxxu的条件下研究了KdVKS方程的适定性问题， 在Hs(R)(s≥1)中证明了方程的整体适定性，Pilod[4]在Hs(R)(s≥-1)证明了方程的局部适定性. 对非线性是(u3)x的适定性问题， 目前还没有相关结果. 本文利用Molinet[6]的方法来研究方程(1)的不适定性问题. 主要结论如下：

2初步结果

方程(1)对应的线性方程是

ut+uxxx-(uxxxx-uxx)+(u3)x=0，

u(0)=φ0

(2)

它的唯一解可以用半群W(t)来表示

(3)

根据Duhamel原理， (2)的解可以表示为积分方程

(4)

引理1α，β是任意实数，t>0， 下列积分不等式成立

(5)

下面的定理在不适定性结论的证明过程中起着关键的作用.

(6)

(7)

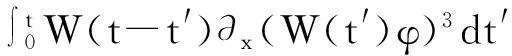
(8)

下面我们取合适的φ来证明(8)是不成立的.

取初值φ定义如下

这里Ψ+(ξ)≥0是一个支集包含在[5/6，1]中的光滑函数， 且对任意的ξ∈[21/24，23/24]，Ψ+(ξ)=1，Ψ+(ξ)=Ψ-(ξ). 注意到对任意的实数s，‖φ‖Hs～1.

下面我们来计算f(x，t)的Hs范数， 其中

对空间变量x作Fourier变换， 得到

(9)

由于对任意的

其中第一项的支集在[5N/2，3N]内，g(t，ξ)的支集在[-3N，7N/6]内. 定义

λ1=ξ13+ξ23+(ξ-ξ1-ξ1)3，β=λ1-ξ3，

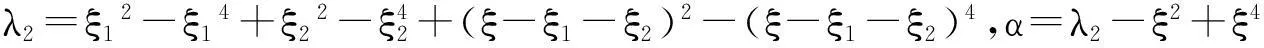
于是有下列估计

=N-3s-3/2exp(t(iξ3+ξ2-ξ4))iξ×

(10)

我们用引理1估计上式中的最后一个积分. 如果ξ1∈[5N/6，N]，ξ2∈[5N/6，N]，ξ∈[5N/2，3N]，则α>0，α～N4，|β|～N3.由引理1可以得到

令N充分大，t充分小， 有

(11)

(11)式代入(10)， 可得

≥C|ξ|N-3s-3/2N-4e-N4t

(χ[21N/24，23N/24]*χ[21N/24，23N/24]*χ[21N/24，23N/24])(ξ)

注意到

=2exp(-11iNξ/12)·sin(Nξ/24)/ξ，

于是

=23exp(-11iNξ/4)·(sin(Nξ/24)/ξ)3，

进一步， 有

(χ[21N/24，23N/24]*χ[21N/24，23N/24]*χ[21N/24，23N/24])(ξ)

=C∫Rexp(ixξ)exp(-11iNx/4)·(sin(Nx/24)/x)3dx.

对充分小的正数γ， 利用变量变换可以得到

(χ[21N/24，23N/24]*χ[21N/24，23N/24]*χ[21N/24，23N/24])(11N/4+γN)

= CN2∫Rcos(γu)(sin(u/24)/u)3du

这就证明了对充分小的正数γ存在不依赖于Ν的常数C， 使得

≥C|ξ|N-3s-3/2N-2e-N4tχ[11N/4-γN，11N/4+γN](ξ)

由此我们可以得到‖f(t)‖Hs的下界

∫11N/4+γN11N/4-γN(1+|ξ|2)s|ξ|2dξ

≥CN-3(2s+1)N-4e-2N4tN2sN3.

进一步， 有

(12)

(12)式说明s<-1当时(8)式是不成立的， 这就证明了定理2.

3主要结论的证明

最后， 我们来证明本文的主要结论.

定理1的证明对φ∈Hs(R)， 考虑Cauchy问题

(13)

其中0<ε<1是一个参数. 如果u(x，t，ε)是(23)的一个解， 那么

(14)

=W(t)φ(x):=u1(x)

进一步， 有

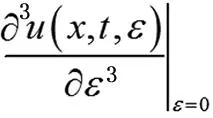
如果从Hs(R)到C([0，T];Hs(R))的解映射是C3的， 一定有

但是上面的估计就是(8)， 在定理2的证明过程中我们已经知道它是不成立的， 这就证明了定理1.

[参考文献]

[1]H.A. Biagioni， J.L. Bona， R. Iorio， M. Scialom， On the Korteweg-de Vries-Kuramoto-Sivashinsky equation， Adv. Diff. Eq. 1:1-20， 1996.

[2]J. Topper， T. Kawahara， Approximate equations for long nonlinear waves on a viscous fluid， J.Phys. Soc. Japan 44:663-666， 1978.

[3]B. I. Cohen， J. A. Krommes， W. M. Tang and M. N. Rosenbluth， Nonlinear saturation of the dissipative trapped-ion mode by mode coupling， Nuclear Fusion， 16:971-992， 1976.

[4]D. Pilod， Sharp well-posedness results for the Kuramoto-Velarde equation， Comm. Pure. Appl. Anal. 7 (4): 867-881， 2008.

[5]X. Zhao， On low regularity of the Ostrovsky， Stepanyams and Tsimring equation[J]， J. Math. Anal. Appl. 378:687-699， 2011.

[6]Molinet L， Ribaud F， On the low regularity of the Korteweg-de Vries-Burgers equation[J]， Int. Math. Res. Not. 37: 1979-2005， 2002.

[7]Esfahani A， Sharp well-posedness of the Ostrovsky， Stepanyams and Tsimring equation， Math. Commun. 18: 323-335， 2013.

[8]Ostrovsky L A， Stepanyams Y A， Tsimring L S， Radiation instability in a stratified shear flow[J]， Int. J. Non-Linear Mech. 19:151-161， 1984.

[责任编辑：张怀涛]

The Ill-posedness for Initial Value Problem of Generalized KdVKS Equation

WANG Hong-wei，SHANG Meng-juan，Xu Guo-xiong

(School of Mathematics and Statistics，Anyang Normal University,Anyang 455000,China)

Abstract:This paper studies the initail value problem of KdVKS equation. By constructing proper initial data，it proves the solution map of KdVKS equation is not C3 in Sobolev space Hs(R)(s<-1). It also get the ill-posedness result of this initial data problem.

Key words:Initial data problem;KdVKS equation; Ill-posedness

[收稿日期]2015-12-06

[基金项目]国家自然科学基金(批准号: 10771166)资助项目; 河南省教育厅科学技术研究重点项目(14B110028); 安阳师范学院大学生创新基金项目(ASCX/2015-Z102)。

[作者简介]王宏伟(1977-)，男，讲师，博士，主要从事偏微分方程和调和分析研究。

[中图分类号]O175

[文献标识码]A

[文章编号]1671-5330(2016)02-0001-03