为思维而教，让小学数学课堂更具张力

□江苏省苏州市吴江区菀坪学校（小学部）　秦永祥



为思维而教，让小学数学课堂更具张力

□江苏省苏州市吴江区菀坪学校（小学部）秦永祥

【摘要】数学是思维的体操，思维训练是数学课堂的最大特色。思维是一种能力，是人类特有的一种精神活动，它把特定事物所引起的特定的暗示，贯穿到底并联成一体。数学教育的最终目的，不是培养鹦鹉学舌的模仿者，而是培养出能够独立思考、独立解决问题的创新型人才。“为思维而教”，发展学生的数学思考，教会学生学会思维，是每一个小学数学教师义不容辞的责任。

【关键词】思维能力思维训练课堂张力

一、学生思维能力的缺失及原因

1.现象扫描：学生思维能力的缺失。

（1）“照本宣科”式的讲授，忽视了数学思想的渗透。日常的数学课堂，依然能看到只带一本数学教材进课堂的老师（不是特级教师，也不是骨干教师，恰恰是一些青年教师），老师教的仅仅是教材上的例题与习题，教学过程没有经过精心设计，课堂没有拓展与延伸，老师站在“教”的角度去考虑学生的“学”，制订教学目标时，只重视知识技能方面的目标，而忽视了学生学习兴趣的激发，忽视了数学思想方法的渗透。

（2）机械程序式的“灌输”，忽视了思维能力的提升。对于新授知识，不少老师采用的方式是“灌输”，以往是“人灌”，近年来随着现代化教学设备引进课堂，“机灌”成为主流方式，很多老师上课就带一个u盘（有的课件还不是自己设计制作的），更有甚者带的是一张与教材配套的光盘。可以想象，学生在机器的统一指令下学习，只能成为答题的操作员，最多是做题的熟练工，忽视了学生的思维训练，何谈思维能力的提升？

（3）“整齐划一”的训练，忽视了思维品质的培养。审视当下的数学课堂，“整齐划一”的学习方式随处可见。小组合作是老师的“惯用手法”，只要老师一说“下面开始小组讨论”，学生马上围坐起来，轮到汇报交流时，往往成为少数几位出色的学生展示自我的机会。课堂上“齐步走”的情况比较突出，即便学生有独特的想法和意见，若是偏离了教师的预设，老师一定会想尽办法将学生拉回自己预设的轨道。这样的课堂，学生缺少了感悟和发现，缺少了思考和表达，缺少了质疑和思辨。

2.原因分析：学生的数学思维怎么了？

（1）教材“束缚”了学生的数学视野。学生的数学学习资源绝大部分依赖于课本。日常教学中许多教师不精心“加工”，拿来就用，即所谓的“教教材”，一定程度上束缚了学生的数学视野，使学生看不到教材以外的丰厚的数学世界。教师的视野决定着学生的视野。教师能把“死知识”教“活”，学生才能把“死知识”学“活”、用“活”。

（2）预设“禁锢”了学生的数学思考。很多老师会依据教材和学生的实际情况精心设计教学流程，甚至有些老师对课堂中的每一个细节都作了详尽周密的计划，更有甚者将哪一个问题让哪一位学生回答都做好安排。这样的设计是基于成人的立场进行预设的，学生的学习完全是在教师预先设计好的轨道内进行，学生不知道为什么这样做，也不知下一步该做什么。因为他们不需要动脑思考，只要用耳朵和嘴巴来配合老师“表演”。

（3）屏幕“蒙蔽”了学生的“数学慧眼”。随着现代教育技术的广泛应用，课堂呈现出多姿多彩的生活情境，学生的眼球被一段又一段的精彩画面深深吸引，课堂上“生活味”浓了，“数学味”却淡了。学生观察到的只是表面现象，很难用数学的眼光去“发现”背后的真相。

二、学生思维能力提升的路径与策略

1.跳出教材学数学，提升思维的高度。如在学生学习运用等式的性质解方程时（苏教版《数学》五年级下册），课标的要求是“了解等式的性质，能用等式的性质解简单的方程”。教材上未出现形如a-x=b这样的方程，而在练习中却出现了12-x=5这一方程。学生出现了以下三种解法：

针对学生出现的三种解法我组织学生交流，让他们充分发表自己的见解。

生1：我是运用等式的性质，将方程的两边同时加上同一个数12。（没等说完，很多学生立马举手持反对意见）

生2：如果x=17，那么代入方程检验，12不够减17，所以这样解肯定不对。（生1点头意识到自己错了）由于这个方程不能运用等式的性质来解，我是利用口算得到答案，只要想12-（）=5就行了。

生3：其实生2的方法就是根据减数等于被减数减差来算的。（师补充：也就是根据加、减、乘、除各部分之间的关系）

生4：我觉得可以用等式的性质，先将方程的两边同时加x，方程变成12=5+x，然后两边交换位置又变成5+x=12，再次运用等式的性质，两边再同时减5就行了。

追问：听懂的同学请举手。（陆陆续续有一半以上的学生都举起了手）看来还有少数同学不太明白，谁再解释一遍？

生5：这里先后两次用到等式的性质。第一次两边同时加x，第二次两边同时减5。

追问：12=5+x变成5+x=12的理由是什么？

生6：根据加法交换律。

真没想到！以往不曾注意的一道习题居然在交流碰撞中激发了学生的潜能，大部分学生在这个过程中表现出极大的兴趣、积极的情感，思维得到升华。与时俱进，与“生”俱进，跳出教材，创造性地处理了教材与教学的关系，较好地实现了“用教材教”。

2.走出“预设”析“生成”，挖掘思维的深度。如学习了梯形的面积计算后，我布置了这样一道课外题：如下图，一面靠墙围一个梯形花坛，围花坛的篱笆长40米，这个花坛的面积是多少？

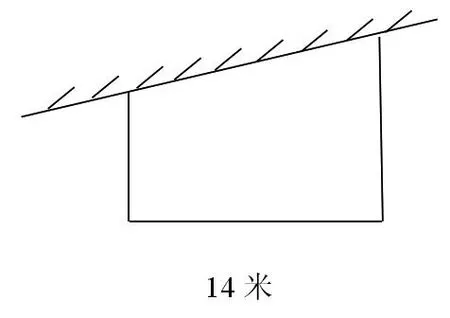
这道题考查的是学生对梯形面积计算的掌握情况。题中直接告诉了梯形的高，而梯形上、下底没有直接给出，但通过篱笆的长可以知道上、下底的和是40-14=26（米），再根据梯形面积的计算方法直接用26×14÷2求出梯形（即花坛）的面积。而在组织交流反馈时学生的做法却完全超出我的预设：

方法1：40-14=26（米）10+16=26（米）（10+16）×14÷ 2=182（平方米）；

方法2：40-14=26（米）12+14=26（米）（12+14）×14÷ 2=182（平方米）；

方法∶3：40-14=26（米）26÷2=13（米）（13+13）×14÷ 2=182（平方米）；

……

显然，学生的思维还仅仅停留在梯形面积计算公式的层面上：要求梯形的面积，必须知道它的上底、下底和高，三者缺一不可。当已经知道上下底的和之后，还是要假设出它的上底和下底，然后才能代入公式求面积。

学生的思维不禁让我陷入了思考：梯形的面积=（上底+下底）×高÷2，教学时，到底是要引导学生理解梯形的面积与“上底”、“下底”和“高”三者都有直接关系，还是与“上下底之和”和“高”有更直接的关系？知道梯形的“上底”和“下底”的目的和作用何在？

当教学概念、法则、公式等一些所谓的“死知识”时，我们习惯地认为就应该把它们“教死”，让学生“死记硬背”。殊不知，这样的教学，学生掌握的永远是“死知识”，解决问题时使用的永远都是“死方法”。学生的真实“想法”向我们传达一个重要的信息——我们的教学还存在很多缺失！

3.透过现象“寻”本质，凸显思维的效度。如在教学“角的度量”时，一位老师精心设计了下面的一道练习题：如图，要求判断∠1和∠2的大小。

由于受两个角的特殊位置的影响，不少学生会被误导，看似∠1将∠2包含在里面。追究深层次的原因，还是这部分学生没有真正理解角的大小的含义，角两边张开的程度决定了角的大小，而不是由其他非本质因素所决定的。小学数学图形知识的教学应基于直观，但不能受限于直观。让学生在观察、想象等活动中，思维从有限迈向无限，由具体走向抽象，源于直观，又超越直观，学生的思维才有发展的空间。

在我们的身边常常发生着这样的情况：老师在台上“津津有味”地讲着，告诉学生“这个概念”应该怎样理解，“这个公式”应该怎样记住，“这道题”应该运用什么知识、什么方法解决……似乎老师讲得很全面、很透彻，但从学生反馈的情况来看，学生的“接受”和老师的“传输”并不成正比。因此，作为小学数学教师的我们真的应该好好反思：教学追求的不是简单的“教给学生一些知识”，而是注重发展学生的数学素养，培养学生的数学情感，提升学生的思维能力。创设符合学生心理需要的学习场景，让学生经历、体验、思考、创造，才能让教师的“教”真正顺应学生的“学”。