承压稳定井流计算的单位分解配点法

郭冬冬，周德亮

(辽宁师范大学数学学院，辽宁 大连 116029)



承压稳定井流计算的单位分解配点法

郭冬冬，周德亮

(辽宁师范大学数学学院，辽宁 大连 116029)

[摘要]用单位分解配点法求解承压含水层中地下水向井的稳定流动问题，该方法摆脱了背景网格的束缚，是一种真正的无网格方法，根据具体模型计算后发现其不仅实施简单，而且计算精度高。

[关键词]单位分解；配点法；稳定井流；无网格

无网格(Meshfree)方法是近几十年来迅速兴起的一种数值计算方法，它很好的克服了有限差分和有限元法等方法需要网格的缺陷，并利用一组散布在求解域中及其域边界上的节点来表示(而非离散)该求解域和其边界，具有收敛快，后处理方便等优点。其中单位分解配点法[1]继承了无网格方法的性质，一方面可以在子域内调节节点的密度，也可以改变某个子域的形状；另一方面局部逼近空间可以包含非多项式函数,从而很好地局部逼近未知解。因此单位分解配点法具有灵活性且近似解有较高的精度。本文将单位分解配点法用于求解地下水的承压稳定井流动的问题。

1配点法

考虑如下定解问题

L{u(x)}=f(x)，x∈D

(1)

B{u(x)}=g(x)，x∈∂D

(2)

其中设D是有界区域，∂D是D的边界，L是偏微分算子，B是边界微分算子，f(x)，g(x)是给定的函数。

(3)

一般情况下中心点取配置节点，αj是待定系数，N是配点总数，φ(‖x-ξj‖2)表示径向基函数[2]，常见的径向基函数有

高斯径向基函数：φ(r)=e-(εr)2(ε>0)；

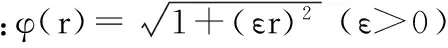
紧支撑径向基函数：φ(r)=(1-εr)4+(4εr+1) (ε>0)；

将(3)代入(1)(2)中，使其分别在内节点，一类边界节点和二类边界节点上成立，这样线性方程组便可写成

Aα=b

(4)

其中α=(α1，α2，…，αN)T是待定的未知向量，

b=(f(x1)，…，f(xN))，g(xNi+1)，g(xNi+N1+1)，g(xN)T

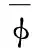
s(x)=φ(x)α=φ(x)A-1u=Ψ(x)u，其中Aα=u，u=[u(x1)…u(xN)]T，

φ(x)=[φ(‖x-x1‖)，…，φ(‖x-xN‖)]，Ψ(x)=φA-1

这里的Ψj(x)具有如下性质

2单位分解配点法

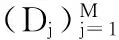
∀x∈DI(x)={j|x∈Dj}，I(x)≤K

集合I(x)表示的是包含x的子域的编号，包含x的子域个数不超过K个，这里常数K与子域的数量M无关。在单位分解配点法[1]中,定解问题的解函数u(x)的近似函数s(x)可以写成下面形式：

(2.1)

其中sj(x)是u(x)在子域Dj内的近似函数，wj是定义在Dj上的紧支正定权函数,它可以通过Shepard的方法构造,即表示为

(2.2)

其中

(2.3)

是子域Dj上的紧支径向基函数.在(2.2)中我们选择Wendland紧支径向基函数

(2.4)

如果对每个节点Xi∈Dj，等式(2.4)中的函数sj(x)，j=1，…，M，都具有局部插值性质sj(xi)=u(xi)，那么全局单位分解近似值继承了局部插值的性质，s(xi)也就可以写成下面的形式：

利用单位分解配点法解决偏微分方程问题时，需要计算在空间微分算子在内部节点上的值和边界微分算子在边界节点上的值，为此需要计算α阶的导数，应用Leibniz定理，可以得到近似解的α阶导数为

其中α和β是多重阶数。

3对井的处理

考虑平面承压稳定井流混合问题[4]

其中,T为导水系数,h(x，y)为水头函数,ε(x，y)为越流补给强度，q为补给量，qk为第k口井的开采量，ρk为第k口井的半径。

通过实际计算可发现，和传统数值方法一样，如果直接从问题中进行离散，用径向基函数配点法求解将会在井口附近产生很大的误差，使结果不可用。原因是井口相对于求解域非常接近为一个点，从数学角度看就是一个奇点，目前解决这一问题的常规方法是将问题转变为如下的等价问题

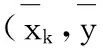
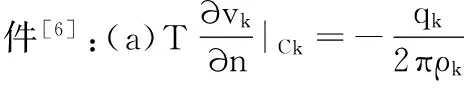
由此求得w,立即得到定解问题的解h=w+v。

图1　计算域及节点配置图

图2　近似解

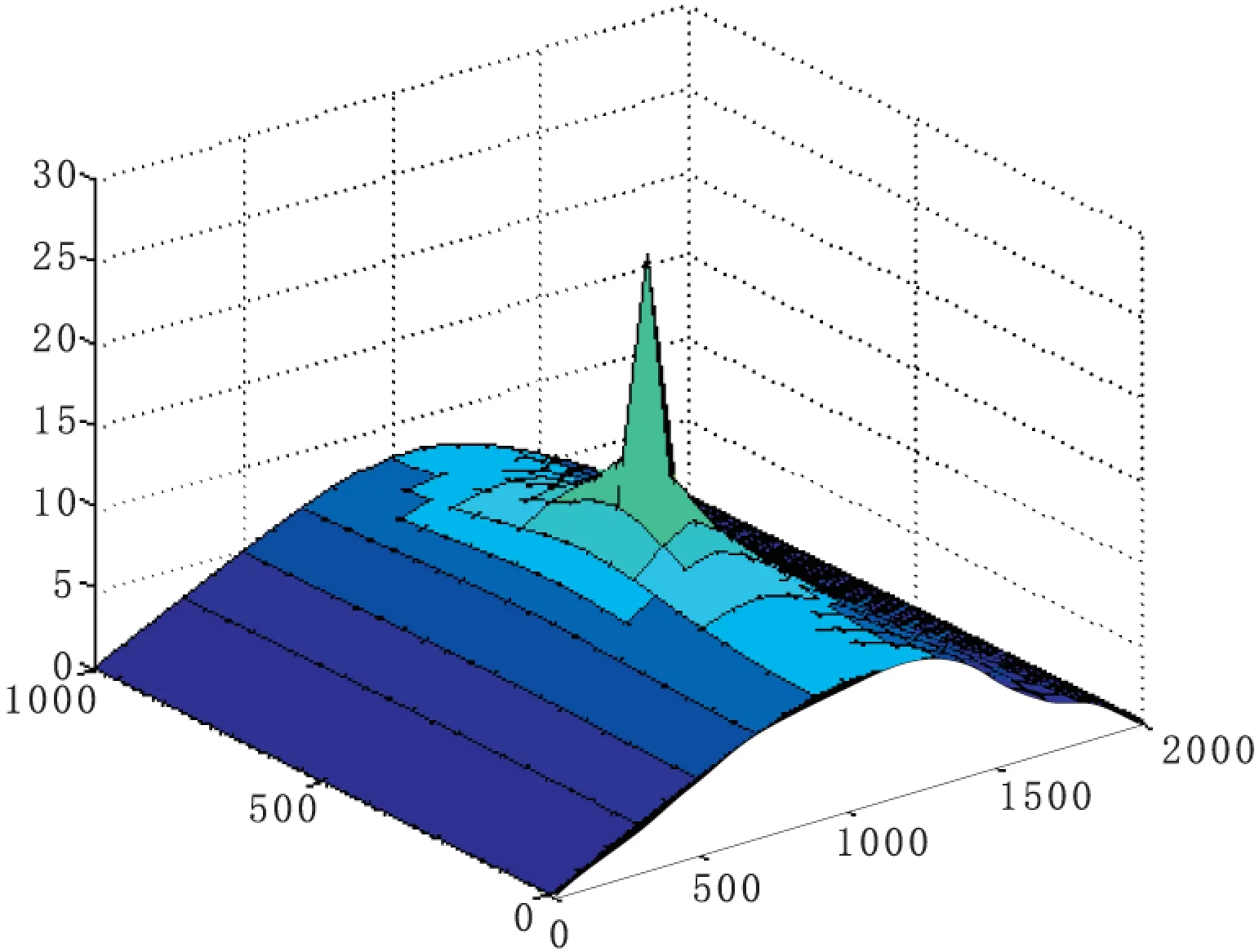
图3　解析解

设ε(x，y)光滑无奇性。要保证数值求解的精度，函数vk除了要满足文[6]给出的前述4个条件

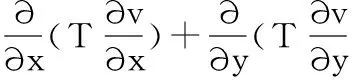
4数值计算

在计算区域上按图1所示布置节点。单位分解配点法得到的水头函数近似解、解析解以及绝对误差如图2、图3和图4所示，本文中选用的是高斯径向基函数，权函数选用紧支径向基函数，参数取160，与解析解比较可知使用单位分解配点法配求解地下水向井流动的问题时具有灵活性，且近似解有较高的精度，由于该方法是在局部区域上应用配点法，因而形成的矩阵是稀疏的，从而减少了计算的费用。

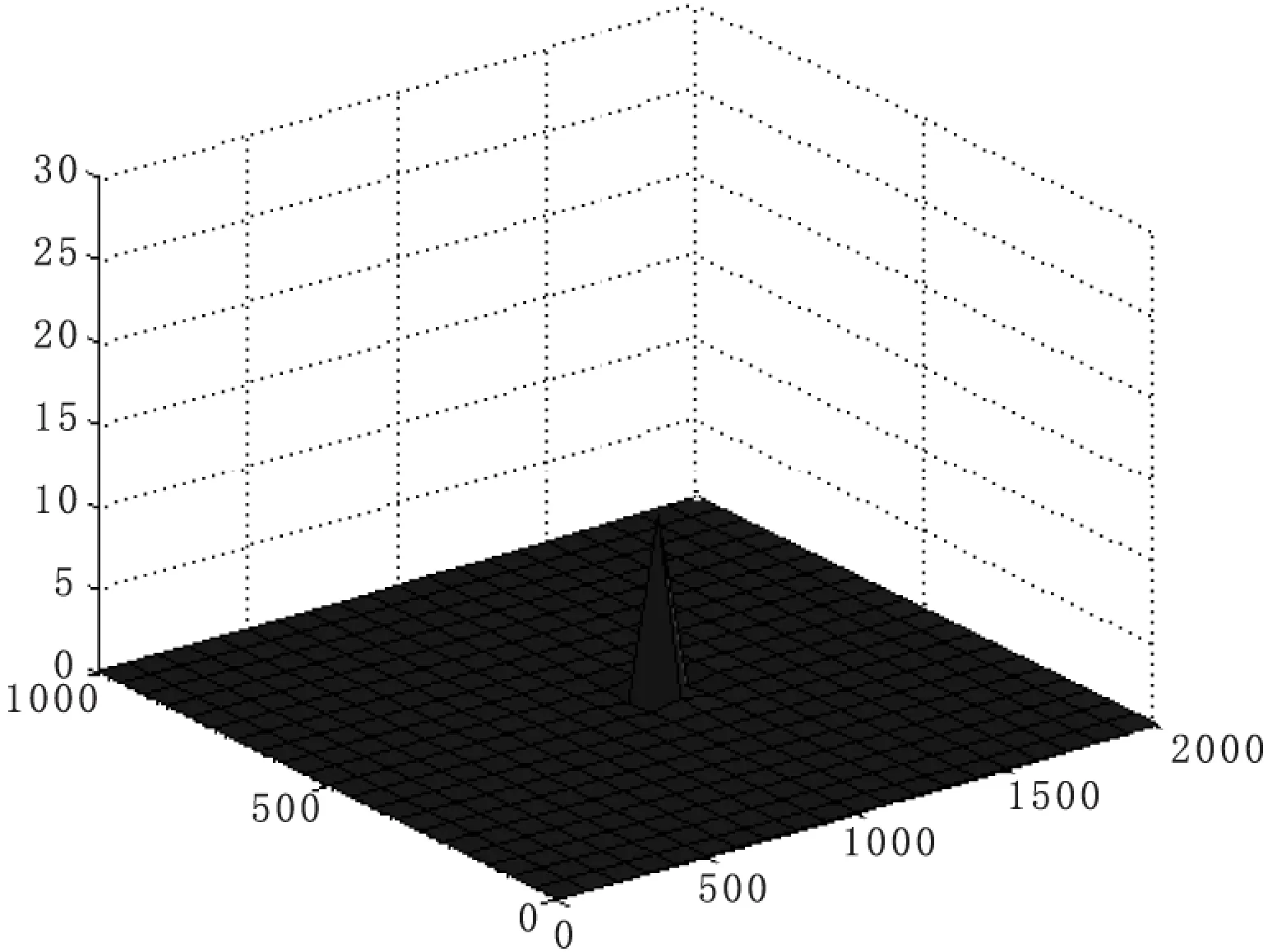
图4　绝对误差

[1]Safdari-Vaighani A,Heryudono A,Larsson E.A Radial Basis Function Partition of Unity Collocation Method for Convection-Diffusion Equations Arising in Financial Applications[J]. Sci.comput,2014.10.4-7.

[2]Sharan M, Kansa E J, Gupta S. Application of multiquadric method fornumerical solution of elliptic partial differential equations[J]. Applied Mathematics Computation, 1997, 84: 275-303.

[3]Franke C, Schaback R. Solving partial differential equations by collocation using radial basis functions[J]. Applied Mathematics Computation, 1998, 93: 73-82.

[4]孙讷正.地下水流的数学模型和数值方法[M]. 北京:地质出版社.1981.7-48,110.

[5]杨天行.非稳定流的有限元法中承压水析奇与潜水逐步析奇的一个方法[J].长春地质学院学报.1978(4): 37-54.

[6]周培德.计算几何——算法分析与设计[M]. 北京;清华大学出版社.1995.88-92.

[收稿日期]2015-11-16

[作者简介]郭冬冬(1991-)，女，辽宁大连人，在读硕士研究生，主攻方向：偏微分数值解法。

[中图分类号]P641.139

[文献标识码]B

[文章编号]1004-1184(2016)01-0051-02