改进BP算法在热流传感器温度补偿中的应用*

康国炼， 杨遂军， 叶树亮

(中国计量学院 工业与商贸计量技术研究所，浙江 杭州 310018)



改进BP算法在热流传感器温度补偿中的应用*

康国炼， 杨遂军， 叶树亮

(中国计量学院 工业与商贸计量技术研究所，浙江 杭州 310018)

摘要:针对帕尔贴(Peltier)热流传感器存在温度漂移问题，提出了一种基于改进BP神经网络的温度补偿模型。采用BP算法的多层前馈网络建立起热流传感器输出电压、实验温度与输入热流间的映射关系,又通过增加动量因子和自适应调节学习率来提高网络的收敛速度与增强网络平稳性。研究结果表明:动量因子—自适应学习率算法温度补偿模型效果明显。

关键词：帕尔贴热流传感器； 动量因子； BP算法； 温度漂移

0引言

随着微量热技术的发展，量热仪在微生物、药物、聚合物、矿物等诸多领域具有广泛的应用[1,2]。帕尔贴(Peltier)热流传感器是微量热系统的核心部件，其本质是半导体热电堆，具有较大的电动势输出，因此,灵敏度很高，能检测到μW量级的热流，相当于的10-6℃的温差[3]。但由于半导体材料具有较大的温度系数，导致传感器的零点和灵敏度具有很强的温度依赖性[4]。为了满足宽温区的微量热精度要求，需要针对温度漂移带来的误差进行补偿。

本文提出了一种基于改进BP算法，即动量因子—自适应学习率算法的温度补偿模型，其利用温度传感器增加了温度参数，并结合热流传感器提供的热流参数建立样本进行学习和训练，通过使用动量因子—自适应学习率算法改善神经网络的收敛性并消除局部最优，使得输入输出参量间的映射关系更加准确可靠，提高了热流检测的准确度。

1帕尔贴热流传感器温度补偿原理

微量量热装置的传热模型如图1所示。

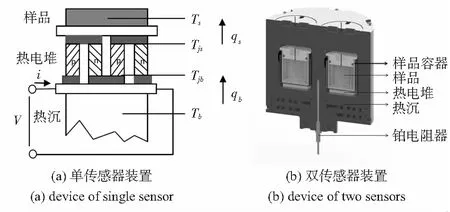
图1　帕尔贴传感器的传热模型Fig 1　Heat transfer model for Peltier sensor

图1(a)中，样品反应时的温度为Ts，热沉温度为Tb并保持恒温状态，由于温差的存在而产生的热流qs经过仔细设计的热流通道，几乎毫无损失地流过热电堆，之后，由热沉吸收，吸收量为qb，并在热电堆的两端平板形成温差ΔT，其中,ΔT=Tjs-Tjb，Tjs和Tjb分别为热电堆两端平板的温度。将塞贝克效应方程应用到实际物理装置可得到

V=Ri+ε(Tjs-Tjb),

(1)

(2)

式中ε为所有热电偶节点的塞贝克系数的之和；R为所有热电偶两端的电阻值之和；kc为所有热导率之和；π为帕尔贴系数，π=Tε，其中,T为绝对温度。因此，可以看出：传感器的输出参量除了与热流qs有关，还与内部电流i和实验温度T有关。但在传统微量热装置中，只有热流qs与传感器输出电压V建立了映射关系，因此,测量误差较大。

图1(b)中在热沉位置上增加了测量实验环境温度的铂热敏电阻器，该热敏电阻器的测温范围为-20～200 ℃。加入了温度传感器以后，将传感器输入参量拓展为热流参数与温度参数，根据式(1)和式(2)建立传感器逆模型

h=f-1(V,t),

(3)

式中h为传感器输入，即目标参量;t为实验温度，即非目标参量;V为传感器输出。在使用A/D转换芯片采集传感器输出电压V时，芯片的输入内阻为无穷大，因此,流经热电堆的电流i几乎为0，其影响可忽略。同时利用具有强大的非线性拟合和学习能力的BP神经网络建立起传感器输出V、环境温度t和热流输入h之间的非线性映射关系。然而热沉温度Tb无法保持绝对恒温，输入热流h带有由实验环境温度波动而引起的寄生热流噪声，即BP网络的误差曲面包含许多极值点，使得BP网络非常容易陷入局部最优甚至无法收敛到给定误差[5]。通过引入动量因子—自适应学习率算法优化网络以后，可以有效解决上述问题。

2基于改进BP神经网络的温度补偿模型

2.1动量因子—自适应学习率算法BP神经网络

BP神经网络拓扑结构如图2所示。

图2　单隐层BP神经网络Fig 2　BP neutral network with single hidden layer

图2中P为输入矢量；R为输入矢量的维数；S1为隐层神经元个数；Wi为神经元权值矩阵；ni为节点输入；ai为输出层节点；Wij为节点连接权值；bi为神经元阈值；fi为各层间地传递函数。

网络输出的误差为E，假如输出误差不在设定误差范围内，则需要将误差回传并修改权值系数Wji(k),修改算法如下

Wji(k+1)=Wji(k)+D(k),

(4)

引入动量因子—自适应学习率算法后，其修改权值为[6]

Wji(k+1)=Wji(k)+η(1-α)D(k)+αD(k-1),

(5)

式中η为学习率，α为带动量因子，α∈(0,1)。从式(7)可以看出:Wji(k+1)的调整不仅与当前的修正量D(k)有关，还与上一步的修正量D(k-1)有关。引入的动量因子相当于阻尼系数，有利于减小训练时的振荡趋势。而学习率η则根据自适应学习率算法调整[7]。当调节误差比设定误差大时，η通过乘以一个递减乘因子d(01)增大η值。这样可以有效降低神经网络对局部误差的敏感程度，防止网络陷于局部极小值。

2.2温度补偿模型

温度补偿模型如图3所示。模型中选取热流传感器输出电压和温度作为输入矢量空间的两个变量，热流作为输出矢量空间的单变量，为了避免量纲对输出结果造成影响，首先对输入输出数据进行标准化处理，将其变换为[-1,1]区间的值。初始化神经网络参数，设置隐层神经元个数为20，神经元阈值为0.01，隐含层传递函数采用s型正切函数tansig，输出层传递函数则采用线性函数pureline。动量因子为0.5，初始学习率为0.01，递增乘因子为1.05，递减乘因子为0.7。采用动量因子—自适应学习率算法优化BP神经网络，对热流传感器进行温度补偿。

图3　热流传感器温度补偿模型Fig 3　Temperature compensation model for heat flux sensor

3帕尔传感器温度补偿实验

为了验证改进BP算法温度补偿模型的效果，采用以TEP—12635热流传感器为核心部件的微量热仪作为实验对象，采集传感器输出电压V，实验温度T以及输入热流功率H。实验温度T设定为60,80,100,120,140 ℃共5个温度点，然后分别在不同温度点下测量不同输入热流时传感器的输出。其中热流由热流校准装置产生，温度则由Pt100热敏电阻器测量。采集的数据如表1所示。

表1　补偿前传感器输出电压

经研究可以发现:若采用标准BP算法进行网络训练，同样设置目标误差为0.01，则无论如何调节学习率都难以收敛。从图4可以看出:改进的BP算法经过1 579次迭代即收敛到预期目标值，其均方差为0.009 994 9。

图4　动量因子—自适应学习率算法训练过程Fig 4　Training process of momentum factor-adaptivelearning rate algorithm

根据改进BP算法补偿以后得到的系统输出热流值随输入热流值变化的曲线如图5所示。

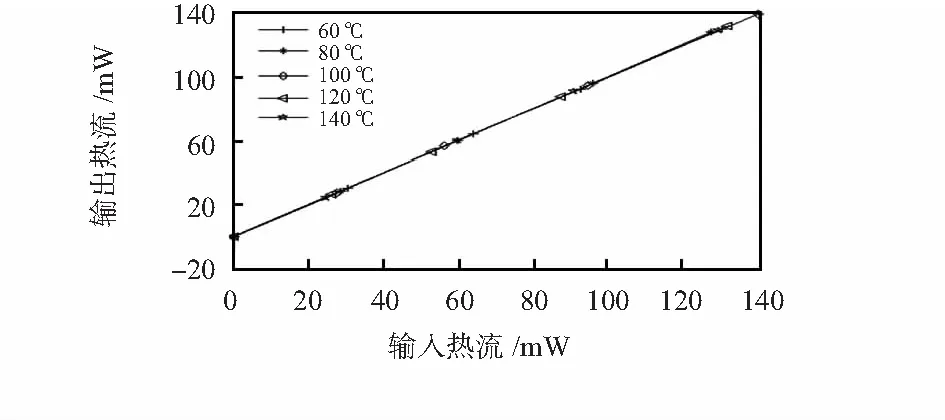
图5　改进BP算法补偿效果Fig 5　Compensation effect of improved BP algorithm

表2为分别采用标准BP算法和改进BP算法进行温度补偿的效果。在温度范围为60～140 ℃，热流检测范围为0～140 mW，采用标准BP算法的精度为6.6 %FS；经过改进神经网络温度误差补偿以后，热流检测的精度为0.14 %FS,温度漂移得到有效抑制。

4结论

本文根据热流传感器温度漂移特性，结合动量因子—自适应学习率BP算法的优点，建立了一个适用于热流传感器的温度补偿模型。通过采用动量因子—自适应学习率算法削弱了网络对局部误差的敏感度，防止网络陷于局部最优，同时提高了网络收敛性，使得在设定较小的目标误差时，网络也可以快速收敛。该温度补偿模型有效降低温度对帕尔贴热流传感器的影响，提高了传感器的准确性。

表2　温度补偿结果

参考文献:

[1]Vittirio Basso,Michaela Kupferling,Carlo P Sasso,et al.A Peltier cell calorimeter for the direct measurement of isothermal entropy change in magnetic materials[J].Review of Scientific Instruments,2008,79(6):063907.

[2]Cristophe Machut,Etienne Gaviot,Pascale Godts,et al.A new Peltier sensor for measuring the thermal conductivity of fluids[J].IEEE Transactions on Instrumentation and Measurement,1998,47(2):398-402.

[3]Zhang Yichao,Jahns Thomas M.Power electronics loss measurement using new heat flux sensor based on thermoelectric device with active control[J].IEEE Transaction on Industry Application,2014,50(6):4098-4016.

[4]Haruyama T.Performance of Peltier elements as a cryogenic heat flux sensor at temperature down to 60K[J].Cryogenics,2001,41(5):335-339.

[5]龚雪飞,徐景,孙寿通,等.PSO-BP神经网络在多元有害气体检测中的应用[J].传感器与微系统,2015,34(2):154-160.

[6]方方.基于改进BP神经网络的电力负荷预测研究[D].哈尔滨:哈尔滨工业大学,2011:30-33.

[7]Zheng Dezhi,Peng Peng,Fan Shangchuan.A research of dynamic compensation of coriolis mass flowmeter based on BP neural network[J].Instrument and Experimental Techniques,2013,56(3):365-370.

Application of improved BP algorithm in temperature compensation of heat flux sensor*

KANG Guo-lian, YANG Sui-jun, YE Shu-liang

(Institute of Industry and Trade Measurement Technique,China Jiliang University,Hangzhou 310018,China)

Abstract:Aiming at temperature drift of Peltier heat flux sensor,a temperature compensation model based on improved BP neural network is proposed.Utilizing multilayer forward network of BP algorithm to build a mapping relationship between output voltage of heat flux sensor,experimental temperature and input heat flux,and by adding momentum factor and adaptively adjust learning rate to increase convergence speed and stabilization of network.Research results show that the temperature compensation model based on momentum factor-adapted learning rate algorithm has obvious effect.

Key words:Peltier heat flux sensor; momentum factor; BP algorithm; temperature drift

DOI:10.13873/J.1000—9787(2016)02—0154—03

收稿日期：2015—06—23

*基金项目：浙江省公益技术研究社发项目(2014C33114)

中图分类号：TP 212

文献标识码：A

文章编号：1000—9787(2016)02—0154—03

作者简介:

康国炼(1990-),男，福建泉州人，硕士研究生，主要研究方向为微量热流检测技术。

叶树亮，通讯作者，E—mail:itmt_paper@126.com。