基于DCT的阵列声波测井数据压缩算法

林　博， 叶朝辉

(清华大学 自动化系，北京 100084)



基于DCT的阵列声波测井数据压缩算法

林博， 叶朝辉

(清华大学 自动化系，北京 100084)

摘要:阵列声波测井是目前一种重要的测井方法。但由于它产生的数据量较大，加之电缆传输速度的限制，测井效率会因此受到影响。为提升测井效率，有必要对原始声波测井数据进行压缩处理。通过分析声波信号的特点，提出了采用DCT+适当量化+算术编码的压缩方法，并根据实际波形的测试结果对压缩方法进行了一系列改进。通过对660组真实测井数据的测试，得到了对于672个点的单极声波数据平均4.56的压缩比，对于1 200个点的偶极声波数据平均9.18的压缩比，均方根误差在2 %左右，证实了该方法的有效性。

关键词：离散余弦变换; 阵列声波测井; 数据压缩

0引言

声波测井是一种重要的地球物理测井方法，它主要利用不同介质中声波的速度、衰减等特性的不同来研究井下的地质结构。

声波测井仪器作为一个嵌入式系统被安置在井内，通过电缆将测井数据上传到上位机进行数据解析。但是，由于声波测井需要利用阵列的大量重复的信息来弥补可能出现的测量误差[1]，因此，数据量较大；而传输线缆能够提供的数据传输速度又是有限的[2]，这样就会极大地影响测井效率。因此，有必要对于井下数据进行压缩处理，传输压缩后的数据，等数据到达地面上位机系统后再进行解压缩处理。这样不仅可以节省传输时间，提高测井效率，同时也能减小对于井下仪器存储空间的需求。

声波测井信号属于一维非平稳信号，对于这样一类信号的压缩处理目前主要采用的思路是变换+量化+熵编码的方式。

文献[3]使用了离散余弦变换(discrete cosine transform,DCT) +差分编码+Huffman编码的方法，利用了心电图(ECG)信号中的周期性特点，在百分比均方根误差 (percent root-mean-square difference,PRD)等于0.61 %的情况下达到了压缩比 (compress ratio,CR)等于16.5的压缩率。文献[4]中作者使用了离散小波变换(discrete wavelet transform,DWT)+神经元网络量化+算术编码对于肌电图数据进行了压缩研究，在PRD等于1.4 %时能够达到CR等于5左右。文献[5]使用了DWT+兰博—立夫—卫曲编码(Lempel—Ziv—Welch encoding,LZW)的压缩算法，用于桥梁振动实时检测数据的压缩处理，在PRD等于0.41 %时能够达到CR等于10.86的压缩率。由于不同种类的信号特性不同，最终得到的CR和PRD也是不尽相同的。

而目前对于声波测井信号的压缩方法研究并不多，文献[6]提出了一种改进的SPIHT方法；文献[7]尝试使用LZW编码对于声波信号进行压缩研究。

本文以DCT +适当量化+熵编码为主要思路对于660组声波测井数据进行数据压缩测试,并依据波形的特点提出改进压缩效果的方法。

1压缩方案设计

1.1声波信号及其特点

声波测井信号分为单极信号和偶极信号，分别由单极子声源和偶极子声源产生。

如图1和图2所示分别是单极阵列声波测井数据和偶极阵列声波测井数据的波形图。单极声波数据共有8个通道，从上到下依次为1～8通道，每个通道672个数据点，每个数据点是从A/D转换得来的16 bit的数据。偶极声波数据同样有8个通道，每个通道有1 200个16 bit的数据点。(图3是偶极数据的前300个数据点)。

图1　单极信号波形图Fig 1　Mono pole signal waveform

图2　偶极信号波形图Fig 2　Dipole signal waveform

图3　偶极信号的前300个点Fig 3　First 300pts of dipole signal waveform

每个通道的单极信号依次分为纵波、横波和斯通利波。而偶极信号除了纵波、横波和挠曲波以外，还有很长的一段信号非常弱的远探测波段。

声波信号有这样一些特点：信号随时间变化而变化，没有什么周期性。频带较丰富，有一定噪声。8通道数据之间有一定的相关性，但又不完全相同。

信号有一定的噪声，也就决定了声波信号的数据并不十分适合使用通用无损压缩的技术进行处理。因为噪声信号带来的随机性会使得无损压缩效果变坏；同时由于有了噪声的干扰，也就意味着即使无误差还原原始信号，意义也并不是很大。所以,压缩方案设计首先对于声波信号做变换编码处理。

1.2DCT

变换编码的基本思想是：通过映射变换，将原始数据投射到一个更为紧凑的表示空间去。在变换域空间重新表示原始数据，可以得到一系列更为有效的系数[8]。从某种意义上说，这些系数集中了更多的能量，减少了不确定性，因而，对于这些系数进行编码需要的总比特数会更少。

这其中，在均方误差度量准则下，失真最小的一种变换方式是K—L变换，但因为该变换包含求解特征向量这一较为困难的操作，致使它并不具有实用性。1974年，Ahmed N等人提出了DCT成为替代K—L变换的准最佳变换。DCT可以得到近似的最优解，同时它又有快速的算法，这使得它在语音和图像处理中都得到了广泛应用[8]。

DCT矩阵A具有以下形式

Ai,j=

通过Y=AX即可求得DCT后的系数矩阵Y。而由于A是一个正交矩阵，因此,反离散余弦变换(IDCT)的变换矩阵

A-1=AT

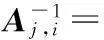
基于DCT的良好特性，使用它作为变换编码方式是非常合适的。

1.3通用无损压缩方法

变换后的系数具有较大的冗余度，可以使用通用无损压缩方法进一步压缩。这其中，LZW字典编码和熵编码较为常用。

但是，LZW变换由于是通过生成字典的方式用较短的字符替代较长的字符，因此,它对于字符的相对位置非常敏感。而声波数据总体来说随机性较强，即使经过DCT后也较难保证有良好的长字符重复性，所以,LZW变换并不适合。

而熵编码则不涉及到字符的相对位置，它只是利用了字符概率这一信息来减小平均码长。可以证明，当概率为pi的字符码长Li等于它的自信息量-lgpi时，平均码长l最小，最小值

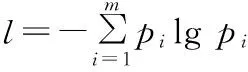
(3)

即字符概率分布的信息熵。

算术编码属于熵编码的一种，它采用化整为零的思想，将各符号的概率值映射为区间的大小，通过区间大小与码字长度的一个对应关系(区间越大，表示该区间的码字长度越短)来实现码字长度对自信息量的逼近。算术编码的效果非常好，可以很好地逼近信息熵。因此，本文采用算术编码作为通用无损编码方法。

算术编码的整个过程如图4所示，假设要对于00,01,10,11这4个字符进行编码，首先在[0,1]区间上根据概率分布给这4个符号划定相应大小的区间，然后找到第一个字符10的区间是[0.5,0.7]。再将这个区间按照符号的概率分布划为4个区间，找第2个字符对应的区间位置，依次类推，最终将得到一个很小的区间，在这个区间中随意找到一个最短的2进制输出，就是最终的编码结果。

图4　算术编码过程示意图 (图片来源文献[9])Fig 4　Process of arithmetic coding

1.4字符统计方法

波形数据是16bit的有符号整型，而使用算术编码需要定义符号，统计它们的概率，则以多少比特为一个整体统计符号的概率才能达到最好的效果就成为一个值得研究的问题。

为了研究这一问题，不妨比较一下以8bit为一个整体进行字符统计的结果和以4bit为一个整体分别对高低字节进行字符统计的结果。

假设对于4bit的高字节的统计概率是[p0,p1,…,p15]，对于其低字节的统计概率是[q0,q1,…,q15]。而8bit的统计概率是[s0,s1,…,s255]。

以4bit为单位的信息熵为

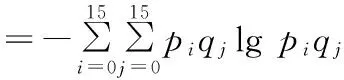
(4)

以8 bit为单位的信息熵为

(5)

因此，H(4)≥H(8)，且只有当si,j=piqj时，即高低位统计概率相互独立时，等号才成立。

基于以上分析，可以得到：H(16)≥H(8)≥H(4)≥H(2)≥H(1),即一般情况下,以更多的bit为单位进行字符概率统计能达到更好的压缩效果。但是，由于还要考虑样本数量的影响，如果位数过多造成样本过少，也会影响信息熵的逼近，因此,这里选择8 bit为统计单位。

2压缩效果与改进

2.1初始压缩效果

如上所述，采用DCT编码，加上以8 bit为单位的算术编码进行压缩测试。由于低8位的数据没有明显的统计规律，因此，考虑舍去。这样做会带来一定的误差，但由于低8位所占数值较小，所占有的能量不大，因此，误差并不大。

选取5个深度点的单极声波数据为样本，CR和PRD的测试结果如表1所示。

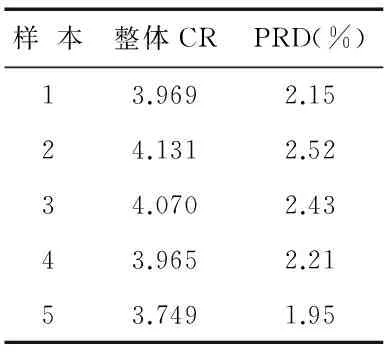
表1　DCT+算术编码+舍去DCT系数低8位后的

可以看到:CR约为4左右，而PRD约为2 %，换算成信噪比(SNR)约为33 dB，这样的信号误差是完全可以接受的。

2.2对DCT编码的分类处理

DCT后的系数(16 bit)呈现低频部分系数大，高频部分系数小的统计规律，如图5所示。

可以利用这样的规律对于DCT系数进行分割统计，前300个系数数值较大，占有的能量较大，但其统计规律不如后372个明显。将二者分开可以使后372个系数达到更好的概率分布。

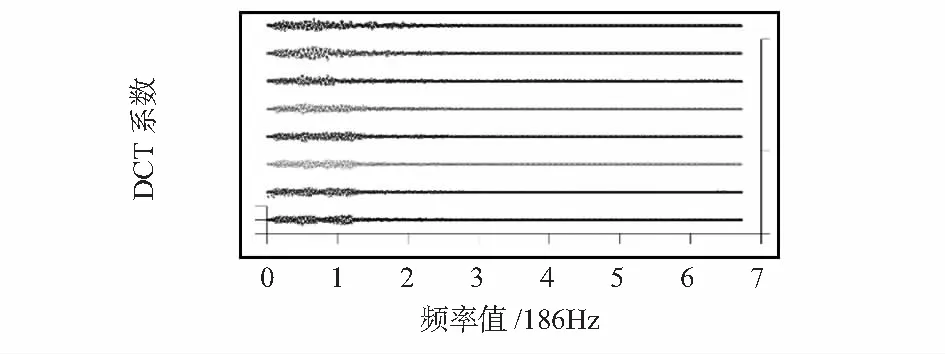
图5　DCT系数的波形Fig 5　Waveform of DCT coefficient

事实上，672个采样点的时间间隔是8 μs，也就意味着最高频率为125 kHz，做完DCT后，DCT系数的频率间隔为186 Hz。而单极声波信号的最高频率只有23 kHz，因此，只有前125个系数拥有较为主要的能量。

同样，对于5个样本进行测试，分割统计后得到的CR如表2所示，可以看到整体CR有了一定的提升。

表2　DCT系数分开处理的CR

2.38通道间的数据关联

阵列声波的数据共有8个通道，这8个通道间的数据是不同的声波接收器采集的，波形数据不尽相同，但是这些数据又来源于同一个采样深度点，因此它们又具有一定的联系。

可以考虑利用通道间数据的关联进一步提升压缩效果。具体做法是将8通道的数据整合到一起做DCT，这样由于数据之间的关联会使得DCT系数呈现出更为集中的特性，从而能达到更好的压缩效果。

5个样本的测试结果如表3所示，可以看到CR又有了一定程度的提高。

表3　合并8通道波形后做DCT得到的CR

3最终的结果

3.1压缩算法流程

最终的压缩算法流程如图6所示，其中虚线框出的是应该在上位机上实现的解压缩步骤。

图6　压缩算法流程框图Fig 6　Flow chart of compression algorithm

3.2660组单偶极数据测试

使用660组单偶极数据进行测试，测试结果的平均值如表4所示。

4结束语

本文着重研究了基于DCT的阵列声波测井数据压缩方法，并根据声波数据自身的特点改进了CR。通过大量的数据测试得出了平均的CR和PRD，进而从理论和实践证实:该方法是行之有效的。

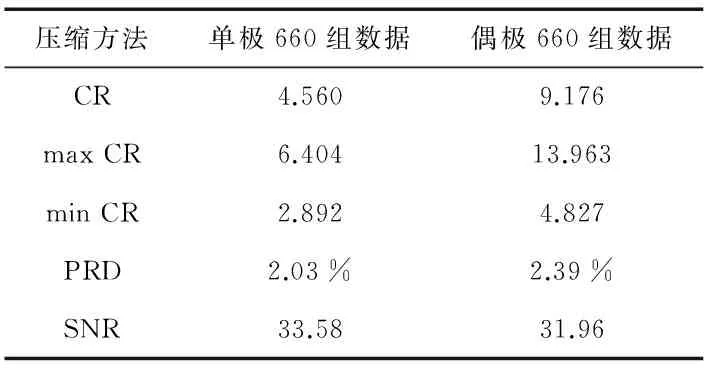
表4　660组数据测试结果

参考文献:

[1]唐晓明,郑传汉,赵晓敏.定量测井声学[M].北京：石油工业出版社,2004.

[2]刘雁飞.基于CAN总线的声波测井地面数据接口与传输系统设计[D].青岛：中国石油大学(青岛),2009.

[3]Lee S J,Kim J,Lee M.A real-time ECG data compression and transmission algorithm for an e-health device[J].IEEE Transactions on Biomedical Engineering,2011,58(9):2448-2455.

[4]de A Berger P,de O Nascimento F A,da Rocha A F,et al.A new wavelet-based algorithm for compression of EMG signals[C]∥2007 The 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society,EMBS 2007,2007:1554-1557.

[5]Zhang Fengyuan,Yang Dong,Gong Xuyan,et al.A wavelet-based data compression algorithm for bridge vibration[C]∥2012 IEEE 14th International Conference on Communication Technology(ICCT),IEEE,2012:334-341.

[6]张伟,师奕兵.声波测井数据压缩的一种 SPIHT改进算法[J].电子测量与仪器学报,2008,22(1):15-19.

[7]叶平凡.声波测井数据压缩算法研究及实现[D].成都：电子科技大学,2012.

[8]吴乐南.数据压缩[M].北京：电子工业出版社,2000：108，112-113.

[9]林福宗.无损数据压缩[DB/OL].[2015—04—01].http:∥source.mastvu.ah.cn/dzjxb/dmtzzsyrj-jm/mxzy/MultiMedia/multimedia/course/course/course1—4—2.html.

Data compression algorithm for DCT-based array acoustic logging

LIN Bo, YE Zhao-hui

(Department of Automation,Tsinghua University,Beijing 100084,China)

Abstract:Array acoustic logging is one of the most important logging methods presently.However,due to its huge amounts of data and the speed limit of data transmission,logging efficiency is restricted.Data compression and processing is necessary to improve logging efficiency.By analyzing characters of acoustic signal,introduce a compression method comprised of DCT,proper quantization and arithmetic coding,further,a series of improvements are made to the method.By test on 660 group real logging data,it is proved that the method is effective,average compression ratio(CR)is 4.56 to the monopole acoustic data of 672 points and 9.18 to dipole acoustic data to 1200 points,with root-mean-square error around 2 %.

Key words:discrete cosine transform(DCT); array acoustic logging; data compression

DOI:10.13873/J.1000—9787(2016)02—0143—04

收稿日期：2015—04—28

中图分类号：TP 274

文献标识码：A

文章编号：1000—9787(2016)02—0143—04

作者简介:

林博(1990-)，男，安徽淮南人，工学硕士，主要从事检测与电子技术方向的研究。