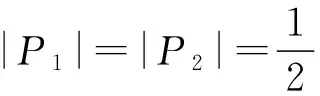Voronoi图的性质及离散构造综述

刘　欣,李海明，刘颖华

(承德石油高等专科学校 社科与数理部，河北　承德　067000)



Voronoi图的性质及离散构造综述

刘欣,李海明，刘颖华

(承德石油高等专科学校 社科与数理部，河北承德067000)

摘要：本文给出Voronoi图的背景和定义以及应用概述，在介绍传统算法的基础上，介绍扩展Voronoi图的离散构造算法，即直接从离散的生成元点出发，而不需要考虑生成元的具体形状，避免了对Voronoi边的形状的计算，对使用计算机算法提供了有效依据。

关键词：Voronoi图；离散Voronoi图；离散构造

Voronoi图概念最早源于以下自然问题：宇航员研究宇宙结构；考古学家试图识别不同部落影响下的地区；气象学家在仪器不灵时估算降雨(雪)量；城市规划者在城市中进行公共学校定位[1]；物流园区范围的设定等。它们虽然表面涉及了完全不同的现象，但具有一点共同之处，即都可以用Voronoi图的概念来解决。

1Voronoi图背景

1.1Voronoi图的定义

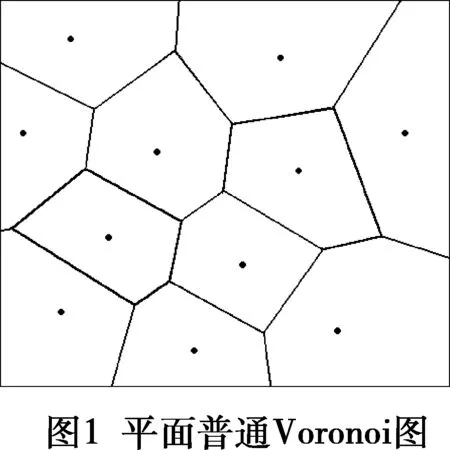
给定平面上有限个(大于1个)孤立点的集合，我们依照欧氏距离将平面上的所有位置点分配给点集中距它最近的点。结果将平面分成了一个网格，这个网格中的区域与平面给出的点集有关，我们称这个网格为由这个点集生成的平面普通Voronoi图，形成Voronoi图的区域为普通Voronoi多边形。在不混淆的情况下，简称普通Voronoi图为Voronoi图，普通Voronoi多边形为Voronoi多边形。

下面给出精确的数学语言描述：

定义设P={p1,…,pn}∈R2,2≤n<∞,xi≠xj(i≠j),i,j∈In={1,…,n}，称由下式

(1)

给出的区域为与点pi关联的普通平面Voronoi多边形，由Vor={V(p1),…,V(pn)}给出的集合为由P生成的平面普通Voronoi图[2](或简称P的Voronoi图)。我们称Voronoi多边形的顶点为Voronoi顶点，V(pi)中的pi为生成元点，集合P={p1,…,pn}为Voronoi图Vor的生成元集。

有时可以简单的将V(pi)记作Vi。用V(xi1,xi2)或V(xi)表示，如果想特别指出生成元集P的Voronoi图，也可以用Vor(P)。图1显示了一个平面普通Voronoi图的实例。

1.2Voronoi图的基本性质

性质1生成元pi的Voronoi区域V(pi)无界的充分必要条件是pi∈BCH(P)，其中，BCH(P)表示生成元集合P的凸壳边界[3]。

性质2n个点的点集P的Voronoi图至多有2n-5个顶点和3n-6条边。

性质3在不退化的情况下，每个Voronoi顶点恰好是三条Voronoi边的交点。

1.3Voronoi图的应用概述

Voronoi图概念最初研究的是有规律的分布于空间上的点，起源于19世纪晚期。经过一百多年的发展，Voronoi图已经广泛应用于实际生活的各个领域。首先是Voronoi图在计算几何理论中的应用，Voronoi图在计算几何当中，常用来解决最近邻近问题；Voronoi图在模式识别领域中也有很多应用，尤其是在机器人路线设计领域中的应用更为突出。同时，也有不少应用对Voronoi图理论提出了新的要求，等待理论上的新成果问世。

2Voronoi图的传统算法

Voronoi图的概念到19世纪70年代早期，发展了许多二维和三维Voronoi图的算法，Voronoi图的构造方法在最近几十年中得到了快速的发展。有半平面的交算法、随机增量等传统算法，随后重点介绍具有较高效率的离散生成算法。

2.1半平面的交算法

半平面的交是生成Voronoi图的最直接的方法。它直接利用Voronoi图的定义，即对点集P中的每一个生成元点pi，确定该点与其它所有生成元点之间的等分线，每条等分线将平面分为两个半平面，构造n-1个半平面的交集，得到点集P的Voronoi图。

2.2随机增量算法

与第一个算法相比，随机增量算法更快速有效。基本思想是数学归纳的“追加法”概念。假设点集P={p1,p2,…,pn}，已构造出k(k

2.3分治法

3Voronoi图的离散构造算法

3.1离散Voronoi图的定义

对屏幕上任一像素点p(x,y)，(0≤x≤k,0≤y≤l)，其中，x和y为整数，k和l分别为屏幕坐标系中横、纵坐标的最大值。设屏幕像素点的集合P={p1,p2,…,pn}，则由像素点pi确定的离散Voronoi区域定义如下：

(2)

由该定义得到的Voronoi图称为二维离散Voronoi图，p1,p2,…,pn为生成元点。如果屏幕上某一像素到两生成元点的距离相等，则该像素属于下标较小的生成元点所在的Voronoi区域(见图2)。

3.2离散Voronoi图构造思想

首先对每一个生成元点指定一种颜色，使不同生成元点之间的颜色互不相同；然后以每个生成元点为圆心，围绕它以该生成元点的颜色画圆；在给像素点涂颜色之前先进行判断：如果该点已经有了颜色，就越过，否则就给该像素点涂上指定颜色；当屏幕上所有的像素点都画上了颜色时，结束。此时，不同颜色的像素之间即为Voronoi边。图3以三个生成元点为例，显示了平面Voronoi图的离散生成过程。

需要注意的是，按照定义，到若干个生成元点距离相等的像素，属于下标较小的生成元点的Voronoi区域。因此，画图时先从下标小的生成元点画起，即按生成元点的下标从小到大画圆。

4Voronoi图的应用

Voronoi图在其它许多方面如：数据压缩、图象处理、通讯中的频率分配[4]、皮肤纹路的模拟、神经网络、地域规划[5]以及物理学、生态学、经营学、调查学、静态学、考古学等学科都有着广泛的应用，此类问题均可由Voronoi图理论及推广成果加以解决。

参考文献：

[1]邓平，王志城.基于Voronoi 图的农村居民点空间分布特征研究[J].地理空间信息,2015(1)：125-127.

[2]周德培.计算几何-算法分析与设计[M ].北京:清华大学出版社, 2000.

[3]刘金义，刘爽.Voronoi图应用综述[J].工程图学学报,2004(2):125-132.

[4]禤家裕.基于Voronoi图的应急通信系统基站选址方法研究[J].信息通信,2014(6)：61-65.

[5]王新生.Voronoi图和非数值随机优化算法在城市与区域规划中的应用研究[D].武汉:武汉大学,2012.

Nature of Voronoi Diagram and Dynamic Structure

LIU Xin, LI Hai-ming, LIU Ying-hua

(Department of Social Sciences, Mathematics and Physics, Chengde Petroleum College,Chengde 067000, Hebei, China)

Abstract:This paper presents the background and definition of Voronoi diagram, and application overview presentation on the basis of the traditional algorithm, it also gives the extension of the discrete Voronoi diagram construction algorithm. That is, starting directly from generators at discrete points without regard to the specific generator shape, which avoids computing Voronoi edge shape, and provides an efficient algorithm for computing.

Key words:Voronoi diagram; dynamic Voronoi diagram, discrete construction

基金项目：承德市软科学研究计划项目(基于Voronoi图的承德物流园区腹地界定及强度提升研究)：20153019；河北省高等学校人文社会科学研究规划项目(高职院校数学课程“模块化-案例驱动-上机实践”三位一体教学模式研究与实践)：GH151013；河北省高等学校科学研究青年基金项目：(高职高专高等数学分级教学的研究与实践)：SQ141019

收稿日期：2015-11-01

作者简介：刘欣(1977-)，女，河北承德人，承德石油高等专科学校社科与数理部副教授，硕士，研究方向为应用数学、计算几何、数学建模等。

中图分类号：TP391.41

文献标识码：A

文章编号：1008-9446(2016)02-0041-03