数据误差处理方法在洪水预报中的应用
丁海蛟,车文刚
(昆明理工大学信息工程与自动化学院,云南昆明 650500)
数据误差处理方法在洪水预报中的应用
丁海蛟,车文刚
(昆明理工大学信息工程与自动化学院,云南昆明 650500)
摘要洪水灾害会对我国的正常农业生产造成非常严重的影响,因此提出一种基于数据误差处理的洪水预报方法有重要意义。结合四川省自贡市某水文站实测的流量数据,应用LS-SVM智能算法建立了单输入单输出(流量—流量)洪水预报模型,并应用数据误差处理方法中改进的拉依达准则法(3σ)和肖维勒准则法(Chauvenet)来处理样本数据里存在的一些误差数据。实验结果表明,应用以上2种数据误差处理方法处理过后的LS-SVM预测模型可以满足洪水预报精度的要求。
关键词流量;LS-SVM;洪水预报;数据误差处理
到目前为止,洪水灾害是全世界范围内最具毁灭性的自然灾害,对正常的农业生产造成了十分严重的影响[1]。为了保障正常的农业生产、保持经济的平稳健康发展,防洪减灾工作是非常必要的。洪水预报在预防洪水和防洪预案的制定工作中一直发挥着非常重要的作用。笔者研究将数据误差处理方法结合LS-SVM智能算法[2]应用到河道的流量预报之中。
1洪水预报研究概况
洪水预报的方法有很多,比较著名的马斯金根洪水演算法就是McCarthy等于1938年对位于美国境内的马斯金根河进行了综合分析以及研究后提出的[3-4],此方法提出之后就迅速地在全世界范围内获得了非常广泛的应用。在此时期内提出的许多模型至今仍然被各个国家的学者广泛应用,此后的科学研究者们还在已有的洪水预报模型基础上提出了很多的改进方法[5]。
我国在洪水预报领域的研究起步比较晚,一直以来采用的是超渗产流的概念[6],此概念是美国学者霍尔顿在20世纪30年代提出来的。我国学者赵人俊在20世纪60年代初期提出了蓄满产流的概念,这个概念是赵人俊在研究了南方流域特性的基础上得到的[7]。目前,国内还没有建立一个可以较好地解决一些普遍性问题的洪水预报系统。我国洪水预报系统的开发,一般都是针对特定的对象、特定的问题或者特定的需求,缺乏通用性。所以,我国目前对洪水预报的研究仍然处于发展的时期,在一些实际的洪水预报作业工作中仍存在很多亟待解决的问题。
2数据误差处理方法
2.1数据误差处理的必要性由于该研究中使用的流量数据是源于天然河道的流量数据采集,通过对所研究区域的所有水文站点进行调查,发现这些原始的流量数据严格意义上说很难准确地反映出所研究流量的客观存在,因为一些人为因素产生的影响,所有的经过测量得到的流量数据都会有误差,而这种有误差的原始流量样本数据一定会影响到LS-SVM所建立预测模型的预测效果,因此要得到比较准确的预测效果,就要剔除这些藏在原始流量数据中的误差数据。该研究应用2种数据误差处理方法进行处理。
2.2改进的拉依达准则法(3σ)拉依达准则法又可以叫做3σ准则法,根据高斯误差理论:当误差服从正态分布之时,它落在[-3σ,3σ]内的概率为99.7%,即异常的数据就是误差的绝对值大于3σ的数据,异常的数据应该被剔除。应用3σ准则法剔除异常数据的步骤如下:

(1)
②计算各个测量值的残差Ui,以及数据列的标准偏差σ,公式分别如下:
(2)
(3)
③各个测量值残差Ui的绝对值和3σ的比较。经过对此方法进行变形改进,可以得到更加简便的方法。根据平均值的定义,可以得到:
(4)
一般情况下,选取的X0应该尽可能地与该测量序列Xi的平均值相接近,并且令Ωi=Xi-X0。
根据变化的贝塞尔公式[8],可以得到:
(5)
这里需要说明的是:因为总体的方差是σ2,而σ2是未知的,样本方差是S2,它是σ2的一个估计值,所以,一般在实际应用时会用3S来代替3σ。

(6)
则将Xi剔除,否则就保留。其中,Kn是与样本容量n有关的系数,可以查表1得到。
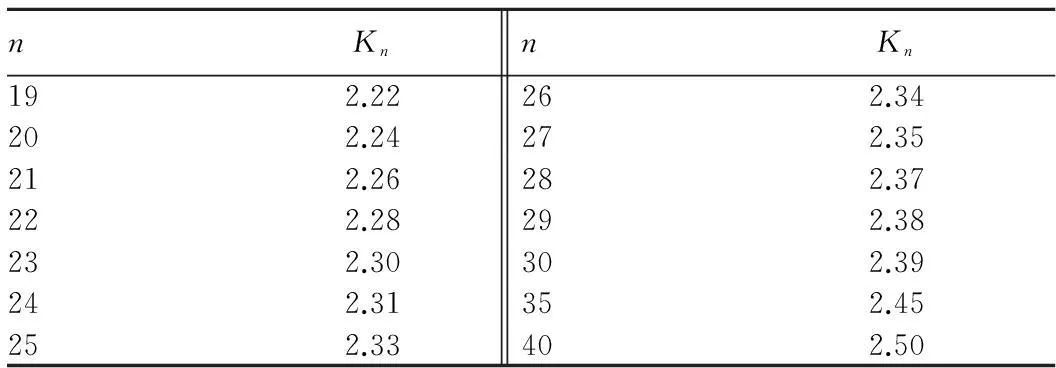
表1 肖维勒准则Kn数据
3 基于数据误差处理方法的LS-SVM预测实验
该研究的整体结构和样本数据误差处理流程如图1所示。

图1 整体结构以及样本数据误差处理流程Fig.1 Processing flow of sample data error and overall structure
3.1数据误差剔除算例取2012年7月10日一天的25个流量数据如表2所示。接下来应用2种方法来剔除这组数据中的异常值。

表2 流量数据
3.1.1改进的拉依达准则法。取X0=61.32,因为Ωi=Χi-Χ0,所以,Ωi的值如表3所示。
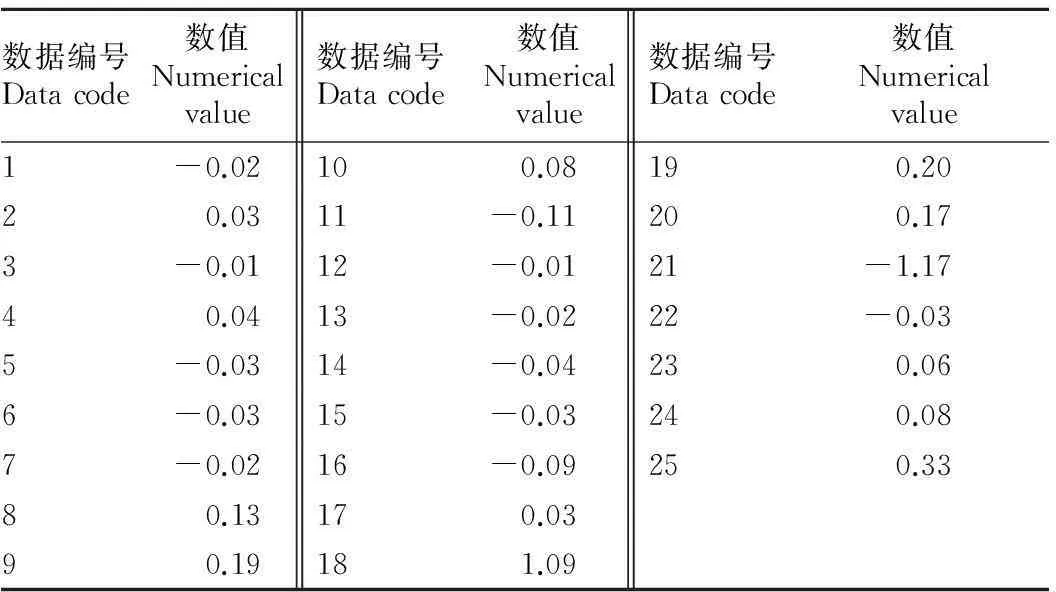
表3 Ωi数据
由于:
(7)
(8)
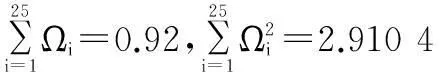


因为以上的这2个极值是正常值,所以这2个极值之间的其他数值肯定也是正常值,也就可以判定目前该组数据中不存在异常值。



经过验证,所剩余其他数据都是正常值,均保留。因为通过改进的拉依达准则法和肖维勒准则法判断所剩余的数据均不存在异常值,所以可以断定经过异常值剔除后的数据中不存在误差数据。
以上2种异常值剔除算法,所剔除的异常值都是最大值和最小值,分析该误差的来源可能是人为因素所造成的粗大误差。因为在此作为算例来进行单组数据的计算是比较简单的,但是该研究中所用到的原始样本数据很多,所以,该研究是借助MATLAB的数据处理功能来进行处理的。
3.2模型预测结果的评定标准为了验证LS-SVM预测模型结果的可行性及其有效性,该研究在此给出预测结果的评定准则。在该研究中所应用的精度评定准则来自于中华人民共和国水利部《水文情报预报规范》(SL250—2000)[9]。接下来给出一些重要参数的取值范围:
①结合现场的实际情况以及中华人民共和国水利部《水文情报预报规范》设置流量的许可误差为:0.9m3/s。
②合格率:
(9)
式中,n是合格预报次数,m是预报总次数;其中,QR≥85.0%时,为甲级精度;70.0%≤QR<85.0%时,为乙级精度;60.0%≤QR<70.0%时,为丙级精度。
③确定性系数:
(10)

④绝对误差:
AE=yc(i)-y0(i)
(11)
式中,y0(i)为实测值,yc(i)为预报值。
⑤相对误差:
(12)
式中,y0(i)为实测值,yc(i)为预报值。
⑥作业预报精度GI为预报误差和许可误差之比。GI≤25.0%,为优秀;25.0%
⑦洪水预报方案的精度等级达到甲级或者乙级,可以用于发布正式的预报;洪水预报方案的精度达到丙级,可以用于参考性预报;洪水预报方案的精度为丙级以下,只能用于参考性估报。
3.3单输入单输出流量预测模型(流量—流量)该研究中采用网格搜索法[10]寻找最优参数,最终确定模型参数γ=0.5,σ2=1.414 2。该研究建立的单输入单输出流量—流量预测模型输入输出示意图如图2所示。

图2 单输入单输出(流量—流量)预测模型输入输出示意Fig.2 Prediction model of single input and single output(flow-flow)
利用2008年7月到2013年7月的数据对模型进行训练后,对2014年7月一共31 d测试集的数据进行预测,预测结果如图3所示。对预测模型输出结果的分析如表4所示。

图3 单输入单输出LS-SVM流量预测Fig.3 LS-SVM flow prediction of single input and single output

验证数据Validationdatam3/sLS-SVM预测数据LS-SVMpredictiondata∥m3/sLS-SVM绝对误差LS-SVMabsoluteerror∥m3/sLS-SVM相对误差LS-SVMrelativeerror%预报是否合格Qualifiedforecastornot107.00106.950.05-0.047合格 91.9092.120.220.24合格 93.8094.060.260.28合格 87.9088.590.690.79合格 61.3064.823.525.74不合格68.3069.040.741.08合格 78.5083.865.366.83不合格101.00100.390.61-0.60合格 151.00150.620.38-0.25合格 104.00104.050.050.05合格 84.7088.193.494.12不合格106.00105.340.66-0.62合格 174.00171.382.62-1.51不合格115.00114.710.29-0.25合格 97.8097.900.100.10合格 94.8095.620.820.86合格
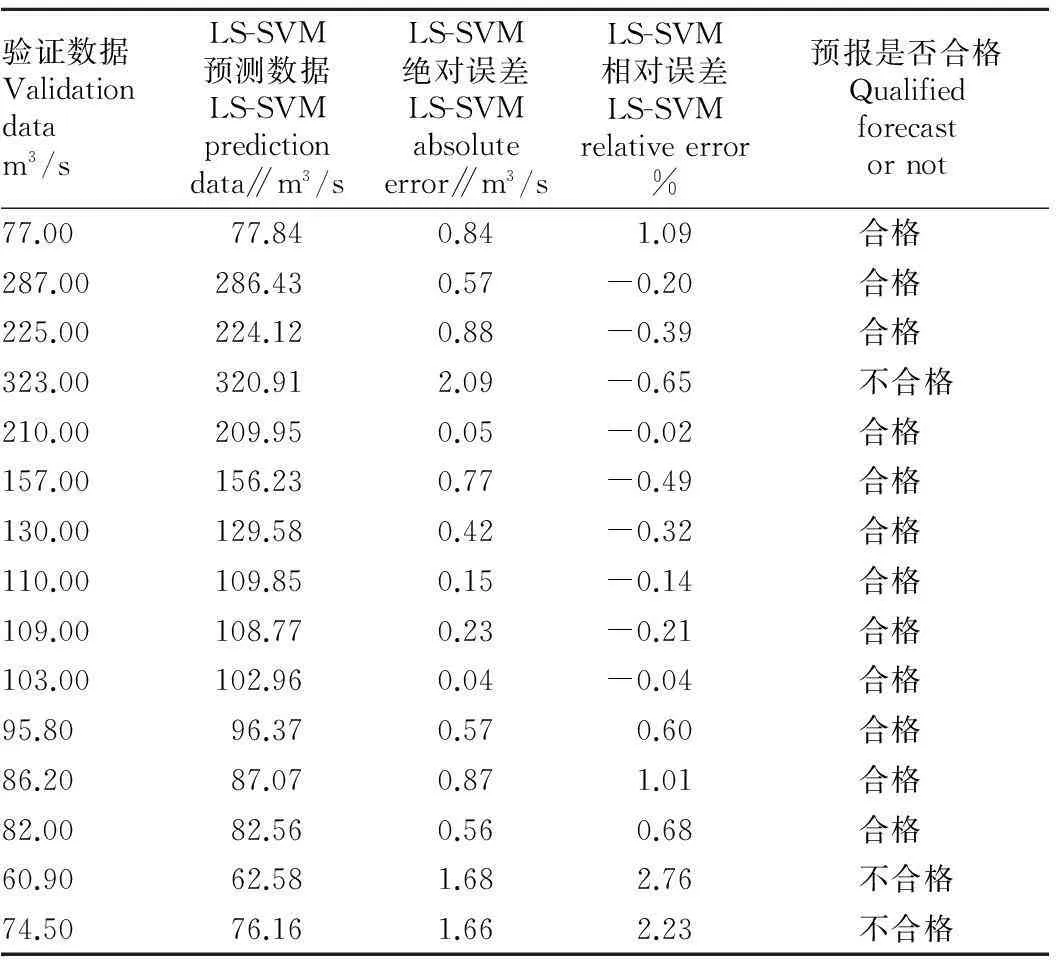
接下表
3.4结果分析经过计算,LS-SVM单输入单输出流量预测模型的QR为77.4%(精度等级为乙);DC=0.899 7(精度等级为乙);GI=98.81%(合格);绝对误差值为0.889 3;相对误差均值为0.733 0%。
根据以上模型精度数据,并依据《水文情报预报规范》(SL250—2000)[9]的相关规定,能够得出:数据误差处理方法结合LS-SVM智能算法所建立的预测模型预测的效果比较好,其精度等级达到了乙级,可以用于发布正式的洪水预报。
4结论
该研究应用数据误差处理的2种方法结合LS-SVM智能算法建立了河道流量预测模型,通过对实例的分析表明:所建立的河道流量预测模型是合理可行的,模型的精度等级达到了乙级,能够用于发布正式的洪水预报,可以为农业生产中防洪方案的制定工作提供十分有效的参考。
参考文献
[1] 徐霞,王静爱,王文宇.自然灾害案例数据库的建立与应用:以中国1998年洪水灾害案例数据库为例[J].北京师范大学学报(自然科学版),2004,36(2):274-280.
[2] 王哲,杨学军,柳林.基于混合智能算法优化LS-SVM的需水预测模型研究[C]//邓坚.中国水文科技新发展:2012中国水文学术讨论会论文集.南京:河海大学出版社,2012.
[3] 孙茂相,孙金根.多水库系统最优控制新算法[J].中国电机工程学报,1990(S1):41-48.
[4] HINO M.On-line prediction of hydrologic system[C]//Proc 15th Cong Int Assoc Hydraul Res.Istanbul,Turkey,1973:121-129.
[5] ABBOTT M B,BATHURST J C,CUNGE J A,et al.An introduction to the European hydrological system-Systeme Hydrologique Europeen,“SHE”,2:Structure of a physically-based,distributed modelling system[J].Journal of hydrology,1986,87(1):61-77.
[6] 高军侠.黄土高原坡耕地超渗产流及作用研究[D].杨凌:西北农林科技大学,2002.
[7] 赵人俊.流域汇流的计算方法[J].水利学报,1963(3):109.
[8] 魏彦玉,王文祥,李宏福.两类含两个变态贝塞尔函数积的积分公式[J].电子科技大学学报,1999,28(1):66-69.
[9] 中华人民共和国水利部.水文情报预报规范:SL250—2000[S].北京:中国水利水电出版社,2000.
[10] 邸欣,崔升佐,孙毓庆.用网格搜索寻优法选择分离6种青霉素类药物的薄层色谱溶剂系统[J].色谱,1996(3):211-213.
Application of the Data Error Processing Method in Flood Prediction
DING Hai-jiao, CHE Wen-gang
(College of Information Engineering and Automation, Kunming University of Science and Technology, Kunming, Yunnan 650500)
AbstractSince the flood disaster causes very serious impacts on normal agricultural production in China, it was of great significance to put forward the flood prediction method based on data error processing. Combining with the flow data measured by a given hydrological station in Zigong City of Sichuan Province, LS-SVM intelligence algorithm was used to establish a single input single output (flow-flow) prediction model. Two kinds of the data error processing method: the improved 3σ method and the chauvenet method to deal with some error data which were hiding in the sample data. The experimental results showed that the application of the above two kinds of data error treatment method used in the LS-SVM prediction model could meet the requirements of flood prediction accuracy.
Key wordsFlow; LS-SVM; Flood prediction; Data error processing
作者简介丁海蛟(1989- ),男,辽宁朝阳人,硕士研究生,研究方向:智能控制。
收稿日期2016-03-16
中图分类号S 422
文献标识码A
文章编号0517-6611(2016)10-257-04

