节段预制胶拼铁路梁静力试验研究

杨树民

(中铁二十二局集团有限公司，北京 100043)



节段预制胶拼铁路梁静力试验研究

杨树民

(中铁二十二局集团有限公司，北京 100043)

摘要：为研究节段预制胶结拼装结构在正常使用阶段和施工状态下的结构行为，结合架梁工况，以模型试验梁模拟其正常使用的荷载工况，测试试验梁的主要静力反应和应力状况，从而验证铁路胶接缝节段拼装结构的结构形式、构造的受力可靠性、安全储备、与相关规范的符合程度。此研究具有一定的理论意义和工程实践应用价值，对同类工程具有一定的借鉴意义。

关键词：节段预制；胶结梁；模型试验梁；静力试验

梁节段胶接拼装结构与整体浇筑结构的区别在于节段拼装接缝处纵向普通钢筋和混凝土为非连续整体，接缝处依靠剪力键及预应力提供的摩擦力传递剪力，依靠预应力产生的压应力传递弯矩。预制的梁节段将通过预应力及剪力键形成整体结构。因此，节段预制胶接拼装梁的构造设计、设计参数取值等应成为节段预制胶接拼装技术首先要解决的问题，直接影响到梁的整体耐久性和结构安全性。

节段预制胶接拼装技术国外起步较早，始于上世纪五十年代。近年来，在国内公路及城市轨道交通行业采用节段预制胶接拼装技术修建了大量的公路及城市轨道交通桥梁，如杭州湾嘉绍大桥、南京长江第四大桥南北引桥、苏通长江大桥、广州地铁4号线等[1]，积累了一定的设计和施工经验，但在铁路行业目前还处于严重滞后的状态。

1 试验目的

通过时速160 kmⅠ级铁路24 m节段拼装(胶拼)工字梁的试制、试验，从而达到验证设计、检验施工工艺、完善设计和施工规范等目的，同时也为胶拼法施工的推广使用提供科学依据，为铁路领域大面积推广应用积累必要经验。

本文主要通过模型梁抗裂性试验和破坏试验，了解铁路节段拼装胶接桥梁的实际破坏形态和安全度，验证设计采用的抗裂、抗弯及抗剪安全系数的安全性及采取的计算公式的合理性，检验节段梁的各项性能指标能否满足设计及运营要求。

2 模型梁主要尺寸

模型梁全长24.9 m，计算跨度24 m，梁高2.1 m，腹板厚0.38 m，顶板宽2.35 m，底板宽1.42 m。梁体沿纵向分为11个节段，10个接缝面，接缝拼装面采用环氧树脂胶粘结。腹板剪力键采用密齿形式。模型梁立面和截面尺寸见图1和图2[2]。

3 混凝土强度和弹性模量

为测试试验模型混凝土的实际抗压强度和弹性模量，在试件预制过程中预留了强度和弹性模量试块。

图1 模型梁立面图(单位：cm)

模型梁混凝土试块抗压强度实测值在62.8～83.7 MPa，其平均值m=72.1 MPa，标准差S=3.8 MPa，95%保证率下的混凝土抗压强度值为65.8 MPa，满足铁路设计规范C60混凝土强度要求。

图2 模型梁截面(单位：cm)

混凝土试块弹性模量实测值在31.1～44.5 GPa之间，试块中实测值≥36.5 GPa的占57.5%，实测值<36.5 GPa的占42.5%。所有实测值的平均值m=37.2 GPa，标准差S=3.0 GPa，95%保证率下的混凝土试块弹性模量值为32.3 GPa，小于铁路设计规范C60混凝土弹性模量要求(36.5 GPa)，偏小约11.5%。

4模型梁静载试验

模型梁静载弯曲试验按《预应力混凝土铁路梁静载弯曲试验方法及评定标准》(TB2092—2003)规定的方法进行。试验等效集中荷载采用5点法加载，跨中设1点集中荷载，其余4点左右对称布置，各加载点沿梁纵向间距为4 m，均作用于工字梁腹板顶面中心。静载弯曲试验加载图式见图3。

为了使试验加载数值准确，静载弯曲试验采用5组门形反力钢架和油压千斤顶来施加竖向荷载，加载反力装置见图4。

图3 模型梁弯曲试验加载图(单位：cm)

图4 模型梁静载试验

4.1 测点布置

(1)静载试验过程中，在梁底缘布置5个挠度测点(百分表)，测试梁体在试验荷载作用下的竖向变形，分别布在跨中、L/4和支点截面底缘。测点布置见图5。

(2)静载弯曲试验中，在接缝1、1′、2、2′、3、3′截面底板下缘横向布置6个百分表，测试接缝处裂缝的开展宽度。测点布置见图6。

图5 静载弯曲试验挠度测点布置

图6 静载弯曲试验底板下缘裂缝宽度测点布置

(3)静载弯曲试验中，在跨中底板下缘沿梁体纵向7.6 m范围内布置外贴振弦式应变传感器，测点编号自东往西为55#～110#，测点间距为0.13 m，应变测试区覆盖跨中区域最关键的4条接缝(接缝1、1′、2、2′)。测点布置见图7。

(4)静载弯曲试验中，在跨中截面布置外贴振弦式应变传感器。测点布置见图8。

(5)静载弯曲破坏试验中，在距两端支座中心线4 m范围内的腹板上布置外贴振弦式应变传感器，监测支点附近区域腹板斜裂缝的出现。测点布置见图9。

(6)在张拉预应力束之前，在跨中节段内选取底板的N2束(南)和N3束(北)各安装1个磁通量传感器，静载试验时进行预应力束拉力的测试。

(7)静载试验过程中，采用5个压力传感器测试加载力，以保证试验荷载的准确施加。

图7 静载弯曲试验底板下缘应变测点布置(单位：cm)

图8 静载试验跨中截面应变测点布置(单位：cm)

4.2 加载循环

模型梁静载弯曲试验共进行了6个加载循环：

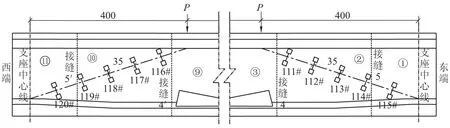
图9 静载弯曲试验支点附近区域腹板斜裂缝应变测点布置图(单位：cm)

(1)第1循环加载至1.0倍设计弯矩，最大荷载为753 kN。

(2)第2循环加载至1.2倍设计弯矩，最大荷载为938 kN。

(3)第3循环加载至1.7倍设计弯矩(梁体下缘开裂)，最大荷载为1 406 kN。

(4)第4循环加载至1.5倍设计弯矩(梁体下缘重裂)，最大荷载为1 223 kN。

(5)第5循环加载至1.8倍设计弯矩(梁体下缘重裂)，最大荷载为1 498 kN。

(6)第6循环加载至2.3倍设计弯矩(超过设计强度)，最大荷载为1 955 kN。

4.3 试验荷载

静载弯曲试验按跨中弯矩模拟进行加载。模型梁设计跨中弯矩为16 800 kN·m，自重跨中弯矩为2 851 kN·m，梁顶实际配重和试验装置自重产生的跨中弯矩为385 kN·m。试验加载前，实际跨中弯矩为3 236 kN·m，支点剪力为591 kN。

通过实测加载值和计算加载值的对比，实际荷载与计算荷载最大相对误差仅为0.9%，说明弯曲试验所加荷载非常准确，满足试验要求。

4.4 挠度结果

模型梁计算挠度时弹性模量取值为36.5 GPa。第1循环加载时，由于梁端节段底板非常不平整，梁底和橡胶板式支座之间存在较大间隙，导致挠度实测值比计算值偏大很多。从第2循环开始，支座板和梁底之间间隙基本压合，故实测结果和计算结果比较接近。从第3循环到第6循环，跨中挠度计算值只计算到消压荷载之前。从荷载挠度曲线看出，跨中挠度实测值大于计算值。随着试验荷载的增大，计算值和实测值的偏差也在增大。

模型梁各加载循环由静活载产生的跨中挠度值为：第2～第6加载循环实测静活载下跨中挠度值的平均值为7.98 mm，计算值为7.40 mm，二者比值为1.078；实测平均挠跨比为1/3 008，计算挠跨比为1/3 243，均小于铁路设计规范1/800要求[3]；梁体实测竖向抗弯刚度比理论计算刚度偏小约7.2%。

4.5 应变结果

模型梁在跨中截面下缘两侧各2 m范围内共布置了应变测点32个，测点编号为6#，20#，30#，68#～96#。

第3循环开裂试验跨中区域下缘应变测点的应变随荷载变化得出：梁体第1条裂缝出现在跨中截面西侧的混凝土实体段上，距离跨中截面为0.91 m的位置(89#测点位置)，对应的开裂荷载FKL=1 160 kN，开裂弯矩为24 116 kN·m，开裂荷载等级(抗裂系数)为1.435。

第4循环重裂试验跨中区域下缘应变测点的应变随荷载变化得出：梁体第1条重裂裂缝出现在跨中截面西侧的混凝土实体段上，距离跨中截面0.39 m的位置(85#测点位置)，对应的重裂荷载FCL=990 kN。

第5循环重裂试验跨中区域下缘应变测点的应变随荷载变化得出：梁体第1条重裂裂缝出现在跨中截面西侧的混凝土实体段上，距离跨中截面0.39 m的位置(85#测点位置)，对应的重裂荷载FCL=970 kN。2次重裂试验得到的平均重裂荷载FCL=980 kN，重裂弯矩为20 876 kN·m，重裂荷载等级(预应力度)为1.243，大于计算值(1.189)，偏大约4.5%。

由开裂和重裂弯矩差计算可得γ×fct=4.39 MPa，其中塑性修正系数γ=1.46(按净截面计算)，由此推算出的实际fct=3.01 MPa。铁路规范提供的C60混凝土轴心抗拉极限强度值fct=3.50 MPa[3]，实测与设计值的比值为0.86，比设计值偏小14%。

由重裂荷载试验跨中区域重裂裂缝位置测点(85#)对应的重裂荷载(980 kN)推算可得：试验加载前跨中截面下缘压应力为23.90 MPa。此阶段理论计算值为22.68 MPa，实测与计算之比为1.054，相对误差为5.4%，说明实测与计算比较接近。

加载开始前，模型梁跨中截面上缘受到的压应力为0.15 MPa，几乎接近零应力状态。故加载到2.3倍设计弯矩时，跨中截面顶板上缘实测的压应变变化值即为混凝土的绝对压应变值。第6加载循环加载至设计极限强度荷载时，跨中截面的主裂缝沿腹板表面向上延伸最高，该截面受压区面积最小，顶板上缘压应变变化也最大。加载至1.5倍设计弯矩之前，跨中截面上缘的压应变随荷载呈线性变化。加载至2.3倍设计弯矩时，实测跨中截面上缘压应变为1 078 με，较小于混凝土抗压极限强度对应的应变(一般在2 000～2 500 με之间)。跨中截面上缘混凝土当前受压状态并未达到真正极限状态，说明该梁体抗弯极限承载力仍有一定的安全储备。

梁端腹板斜向应变测点应变随荷载变化曲线见图10。加载至1.7倍设计弯矩时，东梁端区域腹板表面在靠近接缝5的位置(114#测点位置)出现斜向裂缝；加载至1.83倍的设计弯矩时，西梁端区域腹板表面在靠近接缝5′的位置(119#测点位置)也出现斜向裂缝。斜裂缝见图11和图12。

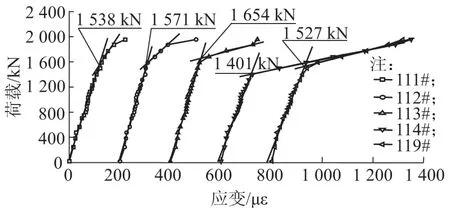
图10 第6循环梁端区域斜向应变测点应变变化

图11 破坏试验东侧斜裂缝

图12 破坏试验西侧斜裂缝

4.6 梁体弹性模量

由荷载弯矩和应力关系推算得出，模型梁跨中节段混凝土弹性模量E=24.4K(K为加载力与跨中截面下缘应变变化值的线性回归斜率)。根据第1、2、3、4、5加载循环推算出的梁体跨中节段混凝土弹性模量分别为36.0 GPa、36.3 GPa、35.9 GPa、36.3 GPa、36.4 GPa，平均弹性模量为36.2 GPa，铁路设计规范提供值为36.5 GPa，二者之比为0.992，基本一致。

4.7 极限承载力

模型梁计算抗弯极限承载力为2.2倍设计弯矩(36.92 MN·m)，试验最大荷载加载至2.3倍设计弯矩(38.43 MN·m)，梁体实际的抗弯承载力大于计算值。

梁端斜裂缝都出现在最外侧加载点到支点之间的4 m区段内，从最外侧加载点截面到变截面起点截面区段内的抗剪承载力基本一致。从变截面起点到支点截面，由于截面积在增大，抗剪承载力也随之增加，抗剪承载力增加幅度大于剪力增加幅度。从梁端斜裂缝实际分布情况看，变截面起点截面基本处于斜裂缝分布区域的中间。综合考虑截面抗剪承载力和实际剪力之间的关系，及斜裂缝分布情况，取变截面起点截面为抗剪承载力计算截面，该截面计算抗剪承载力为5.347 MN。加载至2.3倍设计弯矩时，变截面起点截面所受的剪力为5.352 MN，梁体实际的抗剪承载力大于计算值。加载至2.3倍设计弯矩时，梁体跨中和梁端都未发生破坏，结构抗弯和抗剪极限承载力仍有一定安全储备。

4.8 破坏形态

模型梁破坏试验加载至1.25倍设计弯矩时，底板下缘开始出现横向裂缝；1.7倍设计荷载时，梁端区域腹板表面出现斜向裂缝。加载至2.3倍设计弯矩时，从跨中截面往东6 m范围底板出现28条横向贯通裂缝，从跨中截面往西6 m范围内底板出现25条横向贯通裂缝，裂缝分布比较均匀。东梁端0～6 m范围内南侧腹板出现20条斜裂缝，北侧腹板出现11条斜裂缝。西梁端18～24 m范围内南侧腹板出现19条斜裂缝，北侧腹板出现7条斜裂缝。梁体裂缝分布情况见图13、图14。

图13 南侧腹板破坏试验裂缝分布

图14 北侧腹板破坏试验裂缝分布

接缝1～4和接缝1′～4′下缘均出现开裂，接缝5和5′未开裂，见图15。接缝1～3下缘张开宽度分别为2.74 mm、1.99 mm、0.72 mm；接缝1′～3′下缘张开宽度为3.08 mm、1.91 mm、0.77 mm。接缝1′下缘裂缝张开宽度为全梁最大。

模型梁极限状态中间节段出现的主要是竖向裂缝，且大部分竖向裂缝都向上已发展到重心轴附近。竖向主裂缝出现在中间节段的跨中截面位置，腹板两侧位置基本对称，且延伸高度一致。2.3倍设计弯矩时竖向主裂缝向上延伸到距离顶板和腹板交点为25 cm的位置，主裂缝见图16。梁端区域出现少量斜裂缝，主要集中在重心轴下方，裂缝长度都比较短，裂缝上缘只延伸到重心轴附近，斜裂缝见图11、图12。从裂缝分布图看，模型梁表现为弯曲破坏的特征，且接近整体梁的破坏形态。梁体卸载以后，梁端区域腹板斜裂缝未全部闭合，中间区域节段底板横向贯通裂缝和腹板竖向、斜向裂缝均出现闭合，结构具有较好的裂后性能。

图15 破坏试验梁体张开裂缝

图16 破坏试验跨中主梁裂缝

5 结论

(1)静活载下实测挠跨比为1/3 008，计算值为1/3 243，实测值大于计算值；实测和计算挠跨比均小于铁路设计规范1/800要求。梁体实测竖向抗弯刚度比计算刚度偏小约7.2%。

(2)实测开裂荷载等级(抗裂系数)为1.435，重裂荷载等级为1.243。重裂荷载等级比计算值(1.189)偏大约4.5%。

(3)由开裂和重裂弯矩差推算出的混凝土实际轴心抗拉极限强度值fct=3.01 MPa，与规范设计值(3.50 MPa)之比为0.86，实测值比设计值偏小14%。 (4)试验加载前，跨中截面下缘推算的压应力为23.90 MPa，计算值为22.68 MPa，实测与计算之比为1.054，相对偏差为5.4%，实测与计算比较接近。 (5)2.3倍设计弯矩时，实测跨中截面上缘压应变为1 078 με，较小于混凝土抗压极限强度对应的应变(一般在2 000～2 500 με之间)，跨中截面上缘混凝土受压状态并未达到真正极限状态，该梁体抗弯极限承载力仍有一定的安全储备。

(6)模型梁弹性阶段跨中截面混凝土应变变化符合平截面假定。跨中截面重心轴高度推算值为1.170 m，与计算值1.213 m相差-3.5%，梁体跨中截面各部位结构尺寸控制比较好。

(7)模型梁推算的混凝土弹性模量为36.2 GPa，与设计值36.5 GPa基本一致。

(8)模型梁实际抗弯和抗剪承载力都大于计算值，极限强度计算时不需要折减，规范计算值是偏于安全的。

(9)模型梁极限状态表现为弯曲破坏的特征，且接近整体梁的破坏形态。

6 结束语

由于接缝混凝土界面的处理好坏程度对环氧胶和混凝土表面的粘结抗拉极限强度影响比较明显，施工时应注意节段接缝截面的处理情况。节段预制时，相邻节段接头区段内预应力管道的平顺性应注意加强。

梁体实际抗弯和抗剪承载力均大于规范理论计算值，规范计算公式是合理的，且偏于安全，强度计算时不需要折减。梁体实测竖向抗弯刚度比计算刚度偏小约7.2%，计算抗弯刚度时应适当折减。梁体实际挠跨比、梁端转角、自振频率都能满足设计规范要求值。

参考文献

[1]陈 卓.预制混凝土节段箱梁胶结拼装架设施工[J].桥梁建设，2006(S1)：48-51

[2]中铁第一勘察设计院集团有限公司，北京中铁建北方路桥工程有限公司.新线建设关键技术研究——铁路节段预制胶结拼装梁成套技术研究[R].西安：中铁第一勘察设计院集团有限公司，2014

[3]铁道部.TB10002.1—2005 铁路桥涵设计基本规范[S].北京:中国铁道出版社,2005

A Static-Test-Based Study of the Segment-Precast Glue-Jointed Railway Box Girder

Yang Shumin

(The 22nd Bureau Group of China Railway,Beijing 100043,China)

Abstract:To study the structural behavior of the section-assembled glue-jointed structures both at the normally-used stage and in the state of construction,the true loading condition of it in normal use is simulated,upon the basis of considering the erection construction conditions, with the help of a test model girder,with the main static response and stress condition of the test model girder tested to testify the structural forms of the section-assembled railway glue-jointed structure, the mechanical reliability and the safe reserve of the structure,and the degree of its conformity to the relevant specifications.The research of ours is of certain theoretical and practical engineering importance and may serve as a useful reference for other similar projects.

Key words:precast segments;glue-jointed girder;test beam model；static test

收稿日期：2016-02-23

作者简介：杨树民(1975—)，男，高级工程师，主要从事土木工程施工技术管理工作antcavalier@163.com

DOI：10.13219/j.gjgyat.2016.03.001

中图分类号：U441.5

文献标识码：A

文章编号：1672-3953(2016)03-0001-06