最优的防御策略应对理性的攻击

徐迪迪

(西安电子科技大学 数学与统计学院,陕西 西安　710071)



最优的防御策略应对理性的攻击

徐迪迪

(西安电子科技大学 数学与统计学院,陕西 西安710071)

摘要系统可靠性保护,通常采用投票算法和冗余策略。然而,考虑到系统外界存在攻击者时,系统的可靠性将面临威胁。在文中,主要研究介于系统防御策略和理性攻击者之间的系统可靠性。防御者保证系统可靠性不仅可采取投票算法,还可利用防御资源进行制造伪装组件或保护系统组件;攻击者利用攻击资源随机选择系统中某些簇中组件进行攻击。通过建立模型,解决在给定的攻防资源下,选择最优防御策略应对攻击策略,从而保证系统的可靠性。

关键词系统可靠性;投票算法;冗余;防御策略

可靠性对于许多系统,尤其在军事系统中是重要的。系统可靠性通常利用投票策略[1]和冗余[2]进行保护。但系统处在外界攻击条件下,系统可靠性将会降低。系统应当在防御资源下进行必要的保护,从而提升系统可靠性。防御资源一方面用于保护系统中某些簇中的组件,另一方制造一些伪装组件,干扰攻击者对投票组件的打击[3]。先前已有诸多对提高可靠性的研究。

本文总结文献[4～6]的想法,提出了一种更加适应实际情况的攻防策略模型,以及一种算法,可有效地解决最优的防御策略应对理性的攻击,并提高系统可靠性。

1假设和提出问题

1.1系统模型和假设

假设系统中包含N个相互独立的簇,每个簇中有S个冗余组件,各自冗余组件的可靠性均为p。对于系统中每个簇而言,其可靠性是通过半数投票策略产生正确结果的概率。每一个簇中都能选择自身的一些冗余组件作为投票组件[4]。这些参与投票过程的组件影响着系统的可靠性。在每个簇中,投票组件的数目为Sv,其中1≤Sv≤S。

进一步假设,系统给定总的防御资源Rtd,其能用于加强簇中组件的保护或者制造伪装组件。在每个簇中,被均分到每个簇中的防御资源为Rd,其中Rd=Rtd/N。制造单个伪装组件开销C个单位的防御资源。Sc表示在每个簇中制造的伪装组件的数目,其中Sc×C≤Rd。攻击者分辨不出各个簇中原有组件和添加到每个簇中伪装组件的区别,从降低攻击到投票组件的概率。在每个簇中,剩余的防御资源为(Rd-Sc×C)。其被平均分配用于保护簇中的一些组件。Sp表示每个簇中保护的组件数,其中0≤Sp≤S。因此,在各个簇中,每个被保护的组件上分配的防御资源为rd

(1)

攻击者随机选择系统中某些簇的部分组件进行打击。假设Rta表示全部的攻击资源。攻击者随机挑选h,个簇作为攻击目标h≤n。在每个被攻击的簇中,均分到的攻击资源为Ra,其中Ra=Rta/h。在被攻击的簇中,攻击资源Ra被均分到一些组件上进行攻击,攻击的组件的数目为sa,其中1≤sa≤s+sc。因此,在各个簇中,每个被攻击的组件上分配的攻击资源为Ra

Ra=Ra/sa

(2)

依据文献[8],攻击资源Ra和防御资源RD作用在同一个组件上。若Ra>RD,这个被作用的组件失效,即该组件的可靠性从原有的P直接降为0;若Ra≤RD,该组件保持原有的可靠性P。

1.2未被攻击时单个簇的可靠性计算

当系统中一个簇免于攻击,意味着簇中没有一个组件失效。假设这个簇中选择簇中sv个冗余组件作为投票组件。依据半数以上投票原则,这个簇的可靠性为

(3)

1.3未被攻击时单个簇可靠性计算

假设一个簇被攻击,防御者制定的策略主要选取恰当的保护组件Sp(0≤Sp≤S),投票组件Sv(1≤Sv≤S),制造适当的伪装组件Sc。对于攻击者,其攻击策略主要选择适量的攻击组件Sa(1≤Sa≤S+Sc)。

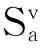
(4)

攻击者击中到投票组件的概率为

(5)

(6)

一个遭受攻击的簇,利用投票原则获得正确结果的概率为

(7)

(8)

经讨论,攻击者击中被保护的投票组件的概率为

(9)

(10)

其中lb=Sa-S-Sc+Sv,以及

(11)

1.4提出问题

假设系统中包含N个相互独立的簇,每个簇中有S个冗余组件,各自冗余组件的可靠性均为p。攻击者利用总攻击资源Rta以及挑选h个簇进行攻击。对于每个被攻击的簇而言,均分到的攻击资源Ra,挑选簇中一些组件进行攻击。与此同时,防御者将总防御资源Rta均分到系统每个簇。在每个簇中,防御资源Rd被用来制造伪装组件Sc和选择保护一些组件Sp。最重要的是挑选簇中的一些组件作为投票组件Sv,参与投票过程。综合以上讨论分析,系统可靠性根据每个簇的可靠性加权可得

(12)

解决的问题可归纳为选择最优sc,sP,sv在攻击者选择h,sa最小化t(sc,sP,sv,h,sa)的情况下使保证t(sc,sP,sv,h,sa)最大化,即

(13)

2提出解决方案

当在每个簇中,选择伪装组件sc的数目为定值,保护组件和投票组件sv的数目可变化。由于投票组件的取值范围介于1～s,被保护的组件sP的取值范围介于0～s,所以系统的总防御策略为nD=(s+1)s。同时,可对防御策略进行按顺序编号,对于给定的sc,第I(1≤I≤na)防御策略对应的每个簇中被保护的组件和投票组件分别为sP=[j/(s+sc)]和sv=I-s×[I/s]+s。

对于攻击者,被攻击簇的范围介于1～n,每个被攻击簇中遭受打击的组件数目取值介于1～(s+sc),从而总攻击策略为na=n(s+sc),第j(1≤I≤na)攻击策略对应的被攻击簇的数目和每个簇中被打击的组件数目分别为h=[j/(s+sc)]和sa=j-(s+sc)×[j/(s+sc)]+(s+sc)。

当攻击策略(h,sa)和防御策略(sc,sP,sv)被确定,系统可靠性可通过公式(10～12)计算求得。因此,可用一个矩阵M=(tI,j)nD×na记录系统的可靠性,其中tI,j表示防御者和攻击者分别选择第I种防御策略和第j种攻击策略时所对应的系统可靠性。

(14)

算法1当每个簇中的伪装组件sc为常量时,求解出系统面临最严重打击情况下选择最优的防御策略D,以及所对应的系统可靠性tmaxmin。

输入可靠性矩阵M=(tI,j)nD×na。

输出tmaxmin和D。

1:Tmaxmin←0;D←0;

2:for i←1 to Nddo

3:Tmin←1

4:for j←1 to Nado

5:if Tmin>ti,jthen

6:Tmin←ti,j

7:end if

8:end for

9:if Tmaxmin

10:Tmaxmin←Tmin

11:set dito 1,and the rest to 0。

12:end if

13:end for

14:return Tmaxmin,D。

算法2当防御和攻击资源都是常量的情况下,求解最终的防御策略。

输入系统中所有簇的数目N;每个簇中冗余组件的数目S;总防御资源Rtd;总攻击资源Rta;制造一个伪装组件的开销C;每个冗余组件的可靠性p。

输出最优的系统可靠性Tmaximun和防御策略(Sc,Sp,Sv)。

1:Tmaxmin←-1;Dfinal←0;

2:Sc←0;Sp←0;Sv←0;

3:for Sc←0 to [Rd/C] do

4:Nd←(S+1)S;Na←N(S+Sc);

5:利用式(12)计算得到可靠性矩阵M

6:利用算法1得到Tmaxmin,D

7:if Tmaximun

8:Tmaximun←Tmaxmin

10:end if

11:end for

12:get i from Dfinal

13:get,Tmaximun,Sc,Sp,Sv

3仿真与实验结果

根据算法2进行实验,主要分析攻击资源和防御资源对防御策略的影响。

在实验中,研究防御资源和防御策略之间的关系。同样设置系统中有10个簇,每个簇中有7个冗余组件,且冗余组件的可靠性均为0.9,制造一个伪装组件开销3个单位的防御资源。总防御资源的数量从100增加到1 100个单位,总攻击资源为400个单位。

图1　总的防御资源与防御策略之间的关系图

图2　最大破坏攻击下的最大可靠性与随机攻击下的可靠性

在图1中,防御策略随着防御资源的增加而不断改变。当防御资源较少时,防御者会在每个簇中保护较少的冗余组件,并选择其作为投票组件参与投票过程。当防御资源不断增加时,防御者制造较多的伪装组件,保护更多的冗余组件并选择其作为投票组件。在图2中,系统的可靠性随着总防御资源的增加而不断增大。同时,系统在最大破坏攻击下的最大可靠性与随机攻击下可靠性之间的差异逐渐减小。因防御资源的不断增加,用于保护投票组件的资源也逐渐增加,从而系统在最大破坏攻击下的最大可靠性不断提高,逼近期望可靠性。

4结束语

本文主要研究在给定总的攻击资源和防御资源下,选择最优防御策略保证系统可靠性。进一步而言,在限制的条件下,提出解决问题的算法。最后通过实验可知:当防御资源少于攻击资源时,防御者在每个簇中选择较少的冗余组件进行保护,并选择被保护的组件作为投票者。反之,当防御资源较为丰富时,防御者制造较多的伪装组件,保护较多的冗余组件充当投票者。

研究过程仍有不足,例如考虑系统结构较为简单。在实际过程中,系统结构十分复杂。系统中每个簇有不同的作用,簇与簇之间还有紧密的联系。因此,下一步准备在复杂的系统模型中研究系统的可靠性和攻防策略。

参考文献

[1]Li Wang,Zheng Li,Ren Shangping.Optimal voting strategy against rational attackers[C].Timisoara,Romania:In 2011 6th International Conference on Risks and Security of Internet and Systems,2011.

[2]Mancini L,Koutny M.Formal specification of n-modular redundancy[C].Roma:CSC’86:Proceedings of the 1986 ACM Fourteenth Annual Conference on Computer Science,1986.

[3]Mokube I,Adams M.Honeypots:concepts,approaches,and challenges[C].Portland:Proceeding 45th Annu.Southeast Regional Conference,2007.

[4]Wang L,Leiferman Y,Ren S,et al.Improving complex distributed software system availability through information hiding[C].UU,USA:Proceeding of ACM Sympore Application Computer,2010.

[5]Hausken K.Strategic defense and attack for series and parallel reliability systems[J].Europe Journal of Operational Research,2008,186(2):856-881.

[6]Levitin G,Hausken K.False targets vs.redundancy in homogeneous parallel systems[J].Reli Engineering System Safety,2009,94(2):588-595.

[7]Tong Z,Kain R.Vote assignments in weighted voting mechanisms[J].IEEE Transactions on Computer,1991,40(5):664-667.

[8]Wang L,Ren S,Yue K,et al.Optimal resource allocation for protecting system availability against random cyber attacks[C].CA USA:Proceeding of 3rd International Conference,ICCRD,2011.

[9]Levitin G,Hausken K.Parallel systems under two sequential attacks[J].Reli Engineering System Safety,2009,94(3):763-772.

Optimal Defense Strategy Against Rational Attackers

XU Didi

(School of Mathematics and Statistics,Xidian University,Xi’an 710071,China)

AbstractSystem reliability is often protected by voting algorithms and redundancy,but is still threatened by attackers.In this paper,the system reliability between system defense strategies and rational attacks is discussed.The Defender can not only choose voting components,but also create camouflaging components and protect system components.The Attacker can choose clusters and components to attack in system.The problem of deciding the optimal defense strategies against attack strategies is modeled with both the defender and the attacker are given fixed resources.

Keywordsreliability;voting algorithm;redundancy;defense strategy

doi:10.16180/j.cnki.issn1007-7820.2016.05.022

收稿日期:2015-10-14

基金项目:国家自然科学基金资助项目(71271165;61373174);陕西省自然科学基金资助项目(2015)

作者简介:徐迪迪(1990—),男,硕士研究生。研究方向:复杂系统可靠性,网络优化。

中图分类号TP393.08

文献标识码A

文章编号1007-7820(2016)05-079-04