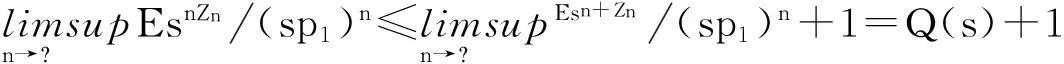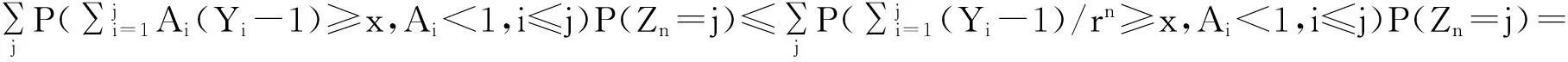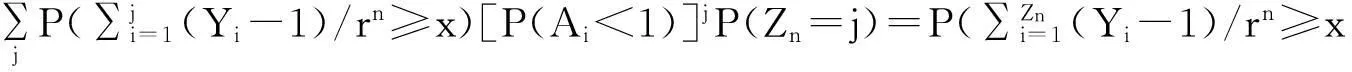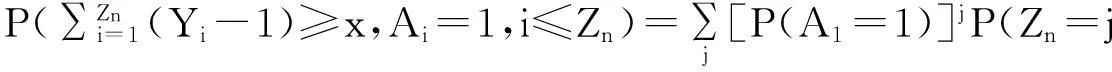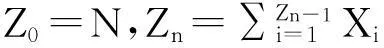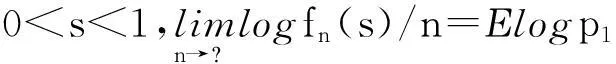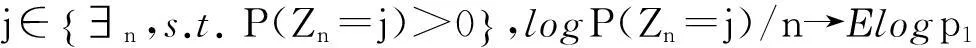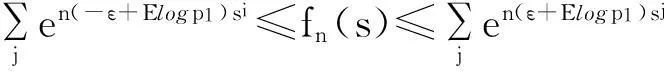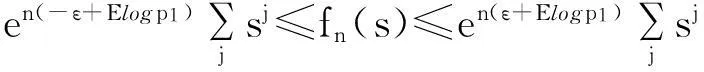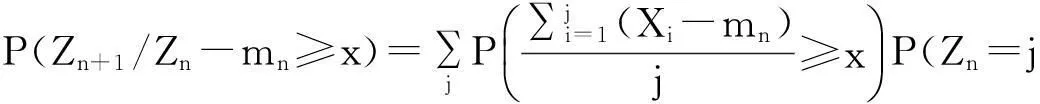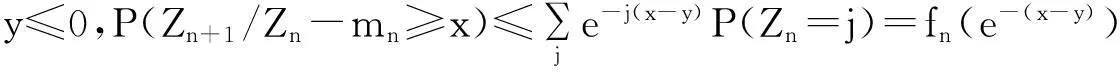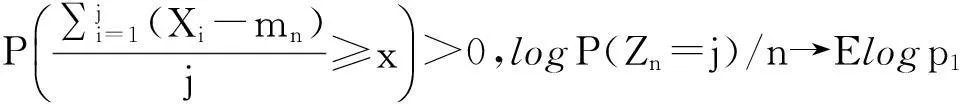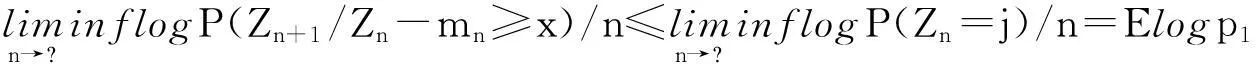分枝过程中的几个极限定理

刘思思

(长沙理工大学 数学与计算科学学院，湖南 长沙 410004)



分枝过程中的几个极限定理

刘思思

(长沙理工大学 数学与计算科学学院，湖南 长沙 410004)

摘要：研究了上临界分枝过程在产生后代机制指数距小于无穷的条件下，一个中偏差率的上界.另外还得到了在随机权重满足一定条件下，Mandelbrot鞅的大偏差以及随机环境中分枝过程的一个大偏差结果.

关键词：分枝过程；Mandelbrot鞅；大偏差；随机环境中分枝过程

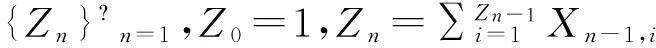
赋予Galton-watson树上每个点v一个Av非负权重,权重之间为i.i.d.且与分枝过程相独立.定义ui为u的第i代祖先，若E(∑|u|=1Au)=1，则Yn=∑|u|=nAu1Au1u2…Au1u2…un为一非负鞅且a.s.收敛到随机变量Z.随机变量Z的性质可见文献[1]，其中分枝过程情形见文献[2-8]，大偏差的性质见文献[9-15].

1主要引理及证明

引理1[16]若存在θ>0使得EeθZ1<，则存在c>0，λ>0使得：

定理1若存在θ>0使得EeθZ1<，则对00，λ>0，使得：

证明由文献[17]定理5，若存在θ>0使得EeθZ1<，则存在c1>0,θ1>0，使得：

继而存在c>0,θ>0使得：P(mtn(W-Wn)>x)≤cexp{-θ3/2xmn[(1/2)-t]}2/3=cexp{-λx2/3(m(2-2t/3))n}.

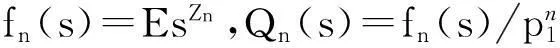
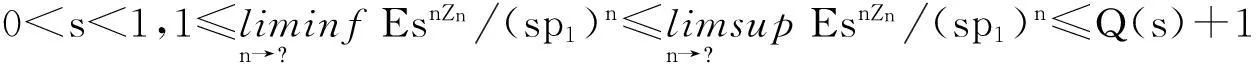
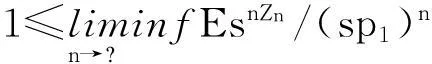
而由于对n>2,{nZn

定理2令P(A1=1)=r>0,假设：

(i)权重与相关分枝过程相独立，Ai≤1,1≤i≤N,a.s.;

(ii)存在t>0满足Eet∑|u|=1Au<；

再由引理2和文献[1]定理2.3，若存在t>0使得Eet∑|u|=1Au<，则存在常数使得:EeθY<θ，I2n以超几何速率退化.而：

2主要结果及证明

因此ε>0，∃N使得n≥N时：-ε+Elogp1≤logP(Zn=j)/n≤ε+Elogp1

(1)

(2)

联立式(1)和式(2)可得出结论.

参考文献:

[1]QuanshengLiu.Ongeneralizedmultiplicativecascades[J].StochasticProcessesandtheirApplications,2000,86(2)：263-286.

[2]RLyons，RPemantle，YPeres.ConceptualproofsoflogLcriteriaformeanbehaviorofbranchingprocesses[J].AnnalsofProbability,1995,4:15-18

[3]Didier.HarmonicContinuous-TimeBranchingMoments[J].AnnalsofAppliedProbability,2007,6:56-89.

[4]KBAthreya，AVidyashankar.LargeDeviationResultsforBranchingProcesses[J].StochasticProcesses,1993,8:59-98.

[5]JDBiggins.AsymptoticpropertiesofsupercriticalbranchingprocessesinrandomenvironmentsGrowthratesinthebranchingrandomwalk[J].ZeitschriftFürWahrscheinlichkeitstheorieUndVerwandteGebiete,1979,5:36-89

[6]JDBiggins.Martingaleconvergenceinthebranchingrandomwalk[J].JApplProbab,1977(3)：25-36.

[7]DPiau.ImmortalbranchingMarkovprocesses:AveragingpropertiesandPCRapplications[J].AnnalsofProbability,2004,32(1A):337-364

[8]IGrigorescu，MKang.Immortalparticleforacatalyticbranchingprocess[J].ProbabilityTheory&RelatedFields,2012，20:45-63.

[9]ODJones.Largedeviationsforsupercriticalmultitypebranchingprocesses[J].JournalofAppliedProbability,2001,4:44-56.

[10] P E Ney,N Vidyashankar.Local limit theory and large deviations for supercritical Branching processes[J].Annals of Applied Probability,2004,4:189-201.

[11]W Chu.Small value probabilities for supercritical multitype branching processes with immigration[J].Statistics or Probability Letters,2014,9:123-156.

[12]O Garet，R Marchand.Large deviations for the chemical distance in supercritical Bernoulli percolation[J].Annals of Probability,2004,5:16-96.

[13]赵博，华志强.BD不同分布的随机变量的和的大偏差[J].湖北民族学院学报(自然科学版)，2015,33(4):396-398.

[14]华志强,董莹,张春生,等.一个不同分布的负相依随机变量的和的不等式[J].内蒙古民族大学学报(自然科学版),2015,30(4):277-279.

[15]陈洋.带有重复分布的宽相依随机变量的随机加权和的精致大偏差[J].苏州科技学院学报(自然科学版),2013,30(4):8-14.

[16]KRISHNA B,Athreya，PETER E.Ney Branching Processes[M].Die Grundlehren der mathematischen Wissenschaften，1972.

[17]ATHREVA K B.Large Deviation Rates for Branching Processes-I[J].Single Type Case Ann Appl Probab,1994,4(3):779-790.

责任编辑：时凌

Some Limit Theorems in Branching Processes

LIU Sisi

(School of Mathematics and Computer Science，Changsha University of Science and Technology，Changsha 410114，China)

Abstract：This paper studies an upper bound of moderate deviation for branching process under some conditions.Otherwise,we aslo get some results of large deviation for Mandelbrot martingale and branching process in random environment.

Key words：branching processes;Mandelbrot martingale;large deviation;branching process in random environment

收稿日期：2016-01-20.

基金项目：长沙市科技计划项目(K1403043-31).

作者简介：刘思思(1991- )，女，硕士生，主要从事分枝过程的研究.

文章编号：1008-8423(2016)01-0042-03

DOI:10.13501/j.cnki.42-1569/n.2016.03.011

中图分类号：O155

文献标志码：A